Correction of characteristics compound longitudinal piezodrive at elastic inertial load for nanorobotics research

doi:10.15406/iratj.2024.10.00291

eISSN: 2574-8092

International Robotics & Automation Journal

Research Article Volume 10 Issue 3

Correction of characteristics compound longitudinal piezodrive at elastic inertial load for nanorobotics research

Afonin SM

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

National Research University of Electronic Technology, Russia

Correspondence: Afonin SM, National Research University of Electronic Technology, MIET, Moscow, Russia

Received: October 22, 2024 | Published: November 14, 2024

Citation: Afonin SM. Correction of characteristics compound longitudinal piezodrive at elastic inertial load for nanorobotics research. Int Rob Auto J. 2024;10(3):103-106. DOI: 10.15406/iratj.2024.10.00291

Download PDF

Abstract

The compound longitudinal piezodrive is used in scanning microscopy, adaptive optics of compound telescope, nanotechnology. For nanorobotics research the compound longitudinal piezodrive is applied. The characteristics of the compound longitudinal piezodrive are determined. Its time constant are founded. The parameters of the compound longitudinal piezodrive for control system with negative feedback on the displacement inductive sensor or on the piezoaccelerometer are determined.

Keywords: compound longitudinal piezodrive, characteristic, time constant correction

Introduction

The compound longitudinal piezodrive is used for nanorobotics research in the nano displacement.¹⁻¹² This compound longitudinal piezodrive based on the piezoelectric effect.⁶⁻²¹ The compound longitudinal piezodrive is applied in nanotechnology, scanning microscopy, adaptive optics, interferometry, microsurgery, nanopump.²²⁻⁵⁴ The deformation this compound longitudinal piezodrive is described with the structural parametric model. By using of mathematical physics method for the compound longitudinal piezodrive with one fixed end its characteristics are determined at elastic inertial load. In the work consider the correction the time constant of the compound longitudinal piezodrive in control system.

Characteristics compound piezodrive

The mathematic model⁶⁻⁵⁴ of the compound longitudinal piezodrive with the control of voltage is determined by using the inverse piezoeffect equation

$S_{3} = d_{33} E_{3} + s_{33}^{E} T_{3}$ $S_{3} = d_{33} E_{3} + s_{33}^{E} T_{3}$

here $S_{3}$ $S_{3}$ , $d_{33}$ $d_{33}$ , $E_{3}$ $E_{3}$ , $s_{33}^{E}$ $s_{33}^{E}$ , $T_{3}$ $T_{3}$ are the relative deformation on 3 axis, the piezomodule, the electric field strength, the elastic compliances at $E = const$ $E = const$ , the mechanic field strength.

By using of mathematical physics method we have the structural parametric model of the compound longitudinal piezodrive with one fixed end^21,22 and its function at elastic inertial load in the form the second order oscillatory link.

Therefore, for the control of voltage the transfer function of the compound longitudinal piezodrive with one fixed end is obtained in the form

$W (s) = \frac{Ξ_{e} (s)}{U (s)} = \frac{d_{33} n}{(1 + C_{e} + C_{33}^{E}) (T_{t}^{2} s^{2} + 2 T_{t} ξ_{t} s + 1)}$ $W (s) = \frac{Ξ_{e} (s)}{U (s)} = \frac{d_{33} n}{(1 + C_{e} + C_{33}^{E}) (T_{t}^{2} s^{2} + 2 T_{t} ξ_{t} s + 1)}$

after transformation this function is determined in the form

$W (s) = \frac{Ξ_{e} (s)}{U (s)} = \frac{k_{t}}{T_{t}^{2} s^{2} + 2 T_{t} ξ_{t} s + 1}$ $W (s) = \frac{Ξ_{e} (s)}{U (s)} = \frac{k_{t}}{T_{t}^{2} s^{2} + 2 T_{t} ξ_{t} s + 1}$

$k_{t} = \frac{d_{33} n}{1 + C_{e} / C_{33}^{E}},$ $k_{t} = \frac{d_{33} n}{1 + C_{e} / C_{33}^{E}},$ $T_{t} = \sqrt{M / (C_{e} + C_{33}^{E})}$ $T_{t} = \sqrt{M / (C_{e} + C_{33}^{E})}$

here $Ξ_{e} (s)$ , $U (s)$ , $k_{t}$ $T_{t}$ , $ξ_{t}$ , $M$ $C_{e}$ , $C_{33}^{E}$ are the Laplace transformation of the displacement second end, the Laplace transformation of the voltage, the transfer coefficient of the compound longitudinal piezodrive, the time constant, the attenuation coefficient, the load mass, the load stiffness, the longitudinal piezodrive stiffness.

Then the transient characteristic of the compound longitudinal piezodrive is determined in the form

$ξ_{e} (t) = k_{t} U_{m} (1 - \frac{e^{- \frac{ξ_{t} t}{T_{t}}}}{\sqrt{1 - ξ_{t}^{2}}} \sin (ω_{t} t + φ_{t}))$

$ω_{t} = \sqrt{1 - ξ_{t}^{2}} / T_{t},$ $φ_{t} = a r c t g (\sqrt{1 - ξ_{t}^{2}} / ξ_{t})$ , $ξ_{m} = k_{t} U_{m}$

here $ξ_{e}$ , $U_{m}$ , $ω_{t}$ , $φ_{t}$ $ξ_{m}$ are the displacement second end, the voltage amplitude, the circular frequency, the phase of oscillations, the steady state displacement.

Microscope MIN-8 was used for experimental observation of resonance frequency. Electronic measuring system model 214 of Caliber plant was used for experimental data of the steady state displacement. For the compound longitudinal PZT piezodrive at $U_{m}$ = 110 V, $d_{33}$ = 4∙10^-10 m/V, n = 8, M = 2 kg, $C_{33}^{E}$ = 6∙10⁷ N/m, $C_{e}$ = 0.6∙10⁷ N/m its parameters $k_{t}$ = 2.9 nm/V, $ξ_{m}$ = 320 nm and $T_{t}$ = 1.74∙10^-4 s are obtained with error 20%.

Correction time constant

Let us consider the correction the time constant of the compound longitudinal piezodrive at elastic inertial load in control system. The time constant of the compound longitudinal piezodrive at elastic inertial load is determined for control system with negative feedback in control system Figure 1 on the displacement inductive sensor in the form $T_{t d i s} = \sqrt{\frac{M / (C_{e} + C_{33}^{E})}{1 + k_{t} k_{d i s}}}$ and after transformation $T_{t d i s} = T_{t} \sqrt{\frac{1}{1 + k_{t} k_{d i s}}}$

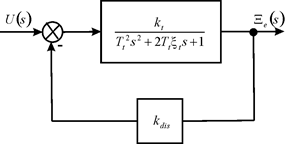
Figure 1 Сontrol system with negative feedback on displacement inductive sensor.

here $T_{t d i s}$ , $k_{d i s}$ are the time constant compound drive in control systems with negative feedback on the displacement inductive sensor and the transfer coefficient of the displacement inductive sensor.

For the compound longitudinal PZT drive at $k_{d i s}$ = 0.1 V/nm, M = 2 kg, $C_{33}^{E}$ = 6∙10⁷ N/m, $C_{e}$ = 0.6∙10⁷ N/m the time constant $T_{t d i s}$ = 1.53∙10^-4 s is obtained. The time constant decreases $T_{t d i s} < T_{t}$ .

Respectively, the time constant compound longitudinal piezodrive in control system Figure 2 with negative feedback on the piezoaccelerometer in the form piezoplate on end of the compound piezodrive has the form

$T_{t a c c} = T_{t} \sqrt{1 + \frac{k_{t} k_{a c c}}{T_{t}^{2}}}$

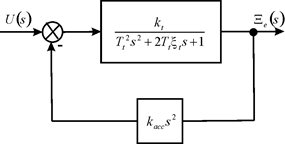
Figure 2 Control system with negative feedback on piezoaccelerometer.

here $T_{t a c c}$ , $k_{a c c}$ are the time constant compound drive in control systems with negative feedback on the piezoaccelerometer and the transfer coefficient of the piezoaccelerometer.

For the compound longitudinal PZT drive at $k_{a c c}$ = 1 Vs²/m, M = 2 kg, $C_{33}^{E}$ = 6∙10⁷ N/m, $C_{e}$ = 0.6∙10⁷ N/m the time constant $T_{t a c c}$ = 1.82∙10^-4 s is obtained. The time constant increases $T_{t a c c} > T_{t}$ .

Discussion

We have transfer function of the compound longitudinal piezodrive with one fixed end and its characteristics by using of mathematical physics method. The deformation the compound longitudinal piezodrive is described with using the structural parametric model. By using mathematical physics method the time constants of the compound longitudinal piezodrive at elastic inertial load are determined in control systems.

Conclusion

The compound longitudinal piezodrive is used for nanorobotics research in the nanodisplacement for nanotechnology, scanning microscopy, adaptive optics, interferometry, microsurgery, nanopump. The parameters of the compound longitudinal PZT drive are obtained.

The characteristics of the compound longitudinal piezodrive are obtained by mathematical physics method. The time constants of the compound longitudinal piezodrive at elastic inertial load are determined for control systems with negative feedbacks on the displacement inductive sensor or the piezoaccelerometer.