Piezoengine for nanomedicine and applied bionics

doi:10.15406/mojabb.2022.06.00164

MOJ

eISSN: 2576-4519

Applied Bionics and Biomechanics

Research Article Volume 6 Issue 1

Piezoengine for nanomedicine and applied bionics

Afonin SM

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

National Research University of Electronic Technology, MIET, Moscow, Russia

Correspondence: Afonin SM, National Research University of Electronic Technology, MIET, 124498, Moscow, Russia

Received: October 28, 2022 | Published: November 11, 2022

Citation: Afonin SM. Piezoengine for nanomedicine and applied bionics. MOJ App Bio Biomech. 2022;6(1):30-33. DOI: 10.15406/mojabb.2022.06.00164

Download PDF

Abstract

The mathematical models of a piezoengine are determined for nanomedicine and applied bionics. The structural scheme of a piezoengine is constructed. The matrix equation is obtained for a piezoengine.

Keywords: piezoengine, structural scheme, nanomedicine and applied bionics

Introduction

A piezoengine is used for nano displacement in tunnel microscopy, for the nano alignment in adaptive optics, microscopy and interferometers in nanomedicine and applied bionics, for the automatic adjustment of the constant optical parameter of the ring quantum generators, for the actively dampen mechanical vibrations in the laser system, for the deform mirrors and operations with penetration in a cells and for the works with a genes.^1–15 A piezoengine with a compact design provides positioning of elements of adaptive systems with an accuracy of up to a nanometer in the range of hundreds of nanometers. These precise parameters of a piezoengine are provided by the use of the reverse piezoelectric effect.^16–48 To calculate the deformations of nano systems, it is required to build the structural scheme of a piezoengine. A piezoengine is used in adaptive optics systems for phase corrections, for example, in an interferometer to adjust maximum of the interference image. In scanning probe microscopy, an image of a surface is formed using a physical probe to scan an object. For example, a scanning tunneling microscope is used to visualize surfaces at the atomic level. Nano movements of the probe along three coordinates X, Y, Z are carried out using a piezoengines.^14–23

Material and methods

A piezoengine works on basis of the reverse piezoelectric effect in the form^3–52

$S_{i} = s_{i j}^{E} T_{j} + d_{m i} E_{m}$

where $S_{i}$ , $s_{i j}^{E}$ , $T_{j}$ , $d_{m i}$ , $E_{m}$ are the relative deformation, elastic compliance, strength mechanical field, piezomodule, strength electric field, i, j . m are indexes.

The differential equation is written^4–52

$\frac{d^{2} Ξ (x, s)}{d x^{2}} - γ^{2} Ξ (x, s) = 0$

Here $Ξ (x, s)$ , s, $x$ , $γ$ are the transform of the deformation, the parameter of the Laplace transform, the coordinate, the propagation factor. For the transverse piezoengine we have at $x = 0$ the first deformation $Ξ (0, s) = Ξ_{1} (s)$ and at $x = h$ the second deformation $Ξ (h, s) = Ξ_{2} (s)$ .

The decision of the differential equation is obtained.

$Ξ (x, s) = {Ξ_{1} (s) sh [(h - x) γ] + Ξ_{2} (s) sh (x γ)} / sh (h γ)$

Where $Ξ_{1} (s)$ , $Ξ_{2} (s)$ are the transforms of the deformations.

At $x = 0$ and $x = h$ we have the system for the transverse piezoengine

$T_{1} (0, s) = \frac{1}{s_{11}^{E}} {\frac{d Ξ (x, s)}{d x} |}_{x = 0} - \frac{d_{31}}{s_{11}^{E}} E_{3} (s)$

$T_{1} (h, s) = \frac{1}{s_{11}^{E}} {\frac{d Ξ (x, s)}{d x} |}_{x = h} - \frac{d_{31}}{s_{11}^{E}} E_{3} (s)$

The mathematical model for the transverse piezoengine has the form.

$Ξ_{1} (s) = {(M_{1} s^{2})}^{- 1} {\begin{cases} - F_{1} (s) + {(χ_{11}^{E})}^{- 1} \\ \times [\begin{array}{l} d_{31} E_{3} (s) - [γ / sh (h γ)] \\ \times [ch (h γ) Ξ_{1} (s) - Ξ_{2} (s)] \end{array}] \end{cases}}$

$Ξ_{2} (s) = {(M_{2} s^{2})}^{- 1} {\begin{cases} - F_{2} (s) + {(χ_{11}^{E})}^{- 1} \\ \times [\begin{array}{l} d_{31} E_{3} (s) - [γ / sh (h γ)] \\ \times [ch (h γ) Ξ_{2} (s) - Ξ_{1} (s)] \end{array}] \end{cases}}$

$χ_{11}^{E} = s_{11}^{E} / S_{0}$

At $x = 0$ and $x = l$ the system in general for a piezoengine is obtained.

$T_{j} (0, s) = \frac{1}{s_{i j}^{Ψ}} {\frac{d Ξ (x, s)}{d x} |}_{x = 0} - \frac{ν_{m i}}{s_{i j}^{Ψ}} Ψ_{m} (s)$

$T_{j} (l, s) = \frac{1}{s_{i j}^{Ψ}} {\frac{d Ξ (x, s)}{d x} |}_{x = l} - \frac{ν_{m i}}{s_{i j}^{Ψ}} Ψ_{m} (s)$

Where $l = {δ, h, b$ the length for the longitudinal, transverse or shift piezoengine.

Therefore, the mathematical model of a piezoengine is determined on Figure 1.

$Ξ_{1} (s) = {(M_{1} s^{2})}^{- 1} {\begin{cases} - F_{1} (s) + {(χ_{i j}^{Ψ})}^{- 1} \\ \times [\begin{array}{l} ν_{m i} Ψ_{m} (s) - [γ / sh (l γ)] \\ \times [ch (l γ) Ξ_{1} (s) - Ξ_{2} (s)] \end{array}] \end{cases}}$

$Ξ_{2} (s) = {(M_{2} s^{2})}^{- 1} {\begin{cases} - F_{2} (s) + {(χ_{i j}^{Ψ})}^{- 1} \\ \times [\begin{array}{l} ν_{m i} Ψ_{m} (s) - [γ / sh (l γ)] \\ \times [ch (l γ) Ξ_{2} (s) - Ξ_{1} (s)] \end{array}] \end{cases}}$

$χ_{i j}^{Ψ} = s_{i j}^{Ψ} / S_{0}$

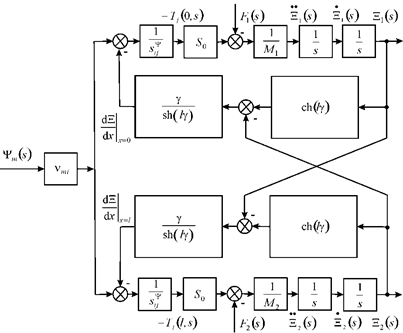
Figure 1 Structural scheme in general of piezoengine.

Where

$v_{m i} = {\begin{matrix} d_{33}, d_{31}, d_{15} \\ g_{33}, g_{31}, g_{15} \end{matrix}$

$Ψ_{m} = {\begin{matrix} E_{3}, E_{3}, E_{1} \\ D_{3}, D_{3}, D_{1} \end{matrix}$

$s_{i j}^{Ψ} = {\begin{matrix} s_{33}^{E}, s_{11}^{E}, s_{55}^{E} \\ s_{33}^{D}, s_{11}^{D}, s_{55}^{D} \end{matrix}$

$γ = {γ^{E}, γ^{D}$

$c^{Ψ} = {c^{E}, c^{D}$

The mathematical model and the structural scheme of a piezoengine on Figure 1 are used for the design of a precise control system in nanomedicine and applied bionics.

The matrix of the deformations is written

$(\begin{matrix} Ξ_{1} (s) \\ Ξ_{2} (s) \end{matrix}) = (\begin{matrix} \begin{matrix} W_{11} (s) & W_{12} (s) & W_{13} (s) \end{matrix} \\ \begin{matrix} W_{21} (s) & W_{22} (s) & W_{23} (s) \end{matrix} \end{matrix}) (\begin{matrix} Ψ_{m} (s) \\ F_{1} (s) \\ F_{2} (s) \end{matrix})$

The settled longitudinal deformations are determined

$ξ_{1} = d_{33} U M_{2} / (M_{1} + M_{2})$

$ξ_{2} = d_{33} U M_{1} / (M_{1} + M_{2})$

For $d_{33}$ = 4×10^-10 m/V, $U$ = 125 V, $M_{1}$ = 1 kg, $M_{2}$ = 4 kg we have the settled deformations parameters $ξ_{1}$ = 40 nm, $ξ_{2}$ = 10 nm and $ξ_{1} + ξ_{2}$ = 50 nm at error 10%.

For the transverse piezoengine at one the fixed face the transfer expression is obtained

$W (s) = \frac{Ξ (s)}{U (s)} = \frac{k_{31}^{U}}{T_{t}^{2} s^{2} + 2 T_{t} ξ_{t} s + 1}$

$k_{31}^{U} = d_{31} (h / δ) / (1 + C_{l} / C_{11}^{E})$

$T_{t} = \sqrt{M / (C_{l} + C_{11}^{E})}$ , $ω_{t} = 1 / T_{t}$

For $M$ = 4 kg, $C_{l}$ = 0.2×10⁷ N/m, $C_{11}^{E}$ = 1.4×10⁷ N/m we have the parameters $T_{t}$ = 0.5×10^-3 s, $ω_{t}$ = 2×10³ s^-1 at error 10%.

The settled transverse deformation has the form

$Δ h = \frac{d_{31} (h / δ) U}{1 + C_{l} / C_{11}^{E}} = k_{31}^{U} U$

For $d_{31}$ = 2∙10^-10 m/V, $h / δ$ = 20, $C_{l} / C_{11}^{E}$ = 0.14 the coefficient is determined $k_{31}^{U}$ = 3.5 nm/V at error 10%.

Conclusion

The mathematical model and the structural scheme of a piezoengine are constructed. The matrix of the deformations of a piezoengine is obtained. The parameters of a piezoengine are determined for the development of a precise control system in nanomedicine and applied bionics.