The structural scheme of a piezoactuator is obtained for astrophysics. The matrix equation is constructed for a piezoactuator. The characteristics of a piezoactuator are received for astrophysics.

Keywords: piezoactuator, structural scheme, nanodisplacement, characteristic, astrophysics

For the control system in astrophysics a piezoactuator of the nanodisplacement is applied in very large telescope, interferometer and orbital telescope.^1–9 The energy conversion is clearly for the structural scheme of a piezoactuator.^10–16 A piezoactuator is used for the nanodisplacement in adaptive optics and telescopes.^17–26

The equations^27–35 of the piezoeffects have form

$\left(D\right)=\left(d\right)\left(T\right)+\left({\epsilon }^T\right)\left(E\right)$

$\left(S\right)=\left(s^E\right)\left(T\right)+{\left(d\right)}^t\left(E\right)$

where $\left(D\right),\left(d\right),\left(T\right),\left({\epsilon }^T\right),\left(E\right),\left(S\right),\left(s^E\right),{\left(d\right)}^t$  are matrixes of electric induction, piezomodule, strength mechanical field, dielectric constant, strength electric field, relative displacement, elastic compliance, transposed piezomodule. The matrixes coefficients we have for a PZT piezoactuator.^36–52

$\left(d\right)=\left(\begin{array}{c}\begin{array}{cccccc}{0}_{}& 0_{}& 0_{}& 0_{}& d_{ 15}& 0\end{array}\\ \begin{array}{cccccc}{0}_{}& 0_{}& 0_{}& d_{ 15}& 0_{}& 0\end{array}\\ \begin{array}{cccccc}{d}_{ 31}& d_{ 31}& d_{ 33}& 0_{}& 0_{}& 0_{}\end{array}\end{array}\right)$

$\left({\epsilon }^T\right)=\left(\begin{array}{ccc}{\epsilon }_{ 11}^T& 0& 0\\ 0& {\epsilon }_{ 22}^T& 0\\ 0& 0& {\epsilon }_{ 33}^T\end{array}\right)$

$\left(s^E\right)=\left(\begin{array}{cccccc}{s}_{ 11}^E& s_{ 12}^E& s_{ 13}^E& 0& 0& 0\\ s_{ 12}^E& s_{ 11}^E& s_{ 13}^E& 0& 0& 0\\ s_{ 13}^E& s_{ 13}^E& s_{ 33}^E& 0& 0& 0\\ 0& 0& 0& s_{ 55}^E& 0& 0\\ 0& 0& 0& 0& s_{ 55}^E& 0\\ 0& 0& 0& 0& 0& 2\left(s_{ 11}^E-s_{ 12}^E\right)\end{array}\right)$

The equation of the mechanical characteristic is written for a piezoactuator

$\Delta l=\Delta l_{\text{max}}\left(1-F/F_{\text{max}}\right)$

where $\Delta l_{\text{max}}=d_{m i}{E}_{m}l$  for $F=0$  and $F_{\text{max}}=d_{m i}{E}_m{S}_0/s_{ij}^E$  for $\Delta l=0$ , $l$  is the length, $S_0$  is the area of a piezoactuator.

For the longitudinal piezoactuator the relative displacement^8–21 is written

$S_3=d_{ 33}{E}_3+s_{ 33}^E{T}_3$

where $d_{ 33}$  is the longitudinal piezomodule.

In the mechanical characteristic of the longitudinal piezoactuator for astrophysics the maximums values of the displacement $\Delta {\delta }_{\text{max}}$  and the force $F_{\text{max}}$  are determined

$\Delta {\delta }_{\text{max}}=d_{ 33}\delta E_3=d_{ 33}U,F_{\text{max}}=d_{ 33}{S}_0{E}_3/s_{ 33}^E$

At $E_3$  = 1.5∙10⁵ V/m, $d_{ 33}$ = 4∙10^-10 m/V, $S_0$ = 1.5∙10^-4 m², $\delta$ = 2.5∙10^-3 m, $s{ }_{33}^E$ = 15∙10^-12 m²/N for the longitudinal piezoactuator are obtained $\Delta {\delta }_{\text{max}}$  = 150 nm, $F_{\text{max}}$  = 600 N with error 10%.

Therefore, for the mechanical characteristic of the transverse piezoactuator we have its maximums values

$\Delta h_{\text{max}}=d_{31}{E}_{3}h=d_{31}Uh/\delta ,F_{\text{max}}=d_{31}{E}_3{S}_0/s_{11}^E$

At $E_3$  = 2.4×10⁵ V/m, $d_{ 31}$ = 2∙10^-10 m/V, $h$  = 1∙10^-2 m,

$\delta$  =0.5∙10^-3 m, $S_0$  = 1∙10^-5 m², $s{ }_{11}^E$ = 12∙10^-12 m²/N the parameters are received $\Delta h_{\text{max}}$  = 480 nm, $F_{\text{max}}$  = 40 N.

The differential equation of a piezoactuator^12–52 is written

$\frac{d^2\Xi \left(x,s\right)}{d{x}^2}-{\gamma }^2\Xi \left(x,s\right)=0$

here $\Xi \left(x,s\right),s,x,\gamma$  are the Laplace transform of the displacement, the parameter, the coordinate and the propagation factor.

The nanodisplacements are obtained for the longitudinal piezoactuator

$\Xi \left(0,s\right)={\Xi }_1\left(s\right)$  for $x=0$

$\Xi \left(\delta ,s\right)={\Xi }_2\left(s\right)$  for $x=\delta$

The decision of the differential equation is determined

$\Xi \left(x,s\right)=\left\{{\Xi }_1\left(s\right)\text{s} \text{h}\left[\left(\delta -x\right)\gamma \right]+{\Xi }_2\left(s\right)\text{s} \text{h}\left(x \gamma \right)\right\}/\text{s} \text{h}\left((\delta )\gamma \right)$

Taking into account the boundary conditions for two faces, we obtain the system of the equations for the structural model of the longitudinal piezoactuator

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{-F_1\left(s\right)+{\left(\chi { }_{33}^E\right)}^{-1}\left[\begin{array}{l}{d}_{33} E_3\left(s\right)-\left[\gamma /\text{s} \text{h}\left(\delta \gamma \right)\right]\\ \times \left[\text{c} \text{h}\left(\delta \gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{-F_2\left(s\right)+{\left(\chi { }_{33}^E\right)}^{-1}\left[\begin{array}{l}{d}_{33} E_3\left(s\right)-\left[\gamma /\text{s} \text{h}\left(\delta \gamma \right)\right]\\ \times \left[\text{c} \text{h}\left(\delta \gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\right\}$

$\chi { }_{33}^E=s{ }_{33}^E/S_0$

where ${\Xi }_1\left(s\right),{\Xi }_2\left(s\right)$  are the Laplace transforms of the displacements for two faces.

We have the system of the equations for the structural model of the transverse piezoactuator

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{-F_1\left(s\right)+{\left(\chi { }_{11}^E\right)}^{-1}\left[\begin{array}{l}d{ }_{31}{E}_3\left(s\right)-\left[\gamma /\text{s} \text{h}\left(h \gamma \right)\right]\\ \times \left[\text{c} \text{h}\left(h \gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{-F_2\left(s\right)+{\left({\chi }_{11}^E\right)}^{-1}\left[\begin{array}{l}{d}_{31}{E}_3\left(s\right)-\left[\gamma /\text{sh}\left(h\gamma \right)\right]\\ \times \left[\text{ch}\left(h\gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\right\}$

$\chi { }_{11}^E=s_{11}^E/S_0$

Therefore, we have the system of the equations for the structural model of the shift piezoactuator in the form

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{-F_1\left(s\right)+{\left({\chi }_{55}^E\right)}^{-1}\left[\begin{array}{l}d{ }_{15}{E}_1\left(s\right)-\left[\gamma /\text{s} \text{h}\left(b \gamma \right)\right]\\ \times \left[\text{c} \text{h}\left(b\gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{-F_2\left(s\right)+{\left(\chi { }_{11}^E\right)}^{-1}\left[\begin{array}{l}d{ }_{31}{E}_3\left(s\right)-\left[\gamma /\text{sh}\left(h\gamma \right)\right]\\ \times \left[\text{c} \text{h}\left(h \gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\right\}$

${\chi }_{55}^E=s_{55}^E/S_0$

The system of the equations for the structural model of a piezoactuator is determined for Figure 1

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{-F_1\left(s\right)+{\left({\chi }_{i j}^{\Psi }\right)}^{-1}\left[\begin{array}{l}{\nu }_{m i}{\Psi }_m\left(s\right)-\left[\gamma /\text{s} \text{h}\left(l \gamma \right)\right]\\ \times \left[\text{c} \text{h}\left(l \gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{-F_2\left(s\right)+{\left({\chi }_{i j}^{\Psi }\right)}^{-1}\left[\begin{array}{l}{\nu }_{m i}{\Psi }_m\left(s\right)-\left[\gamma /\text{s} \text{h}\left(l \gamma \right)\right]\\ \times \left[\text{c} \text{h}\left(l \gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\right\}$

${\chi }_{i j}^{\Psi }=s_{i j}^{\Psi }/S_0$

where

$v_{m i}=\{\begin{array}{c}{d}_{ 33},d{ }_{31},d{ }_{15}\\ g{ }_{33},g{ }_{31},g{ }_{15}\end{array}$

${\Psi }_m=\{\begin{array}{c}{E}_3,E_3,E_1\\ D_3,D_3,D_1\end{array}$

$s_{i j}^{\Psi }=\{\begin{array}{c}s{ }_{33}^E,s{ }_{11}^E,s{ }_{55}^E\\ s{ }_{33}^D,s{ }_{11}^D,s{ }_{55}^D\end{array}$

$l=\{\delta ,h,b$

$\gamma =\{{\gamma }^E,{\gamma }^D$

$c^{\Psi }=\{c^E,c^D$

The structural scheme on Figure 1 is used for the decision of a piezoactuator in astrophysics. The matrix of the nanodisplacement of a piezoactuator has the form.

$\left(\begin{array}{c}{\Xi }_1\left(s\right)\\ {\Xi }_2\left(s\right)\end{array}\right)=\left(\begin{array}{c}\begin{array}{ccc}{W}_{ 11} \left(s\right)& W_{ 12} \left(s\right)& W_{ 13} \left(s\right)\end{array}\\ \begin{array}{ccc}{W}_{ 21} \left(s\right)& W_{ 22} \left(s\right)& W_{ 23} \left(s\right)\end{array}\end{array}\right)\left(\begin{array}{c}{\Psi }_m\left(s\right)\\ F_1\left(s\right)\\ F_2\left(s\right)\end{array}\right)$

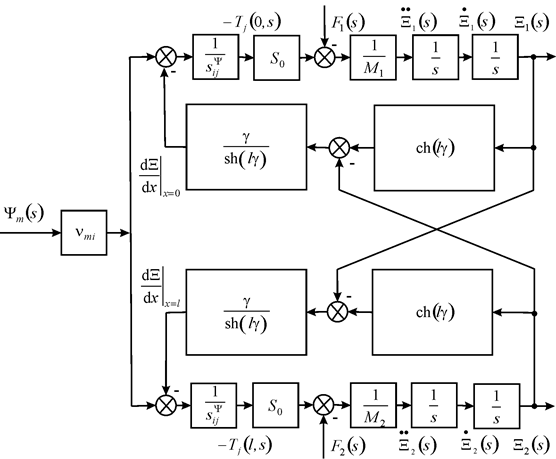
Figure 1 Structural scheme of piezoactuator.

The steady-state nanodisplacements are written for two faces of a piezoactuator

$\begin{array}{l}{\xi }_1=d_{m i}{\Psi }_m l M_2/\left(M_1+M_2\right)\\ {\xi }_2=d_{m i}{\Psi }_m l M_1/\left(M_1+M_2\right)\end{array}$

The steady-state nanodisplacements are obtained for two faces of the longitudinal piezoactuator

$\begin{array}{l}{\xi }_1=d_{ 33} U M_2/\left(M_1+M_2\right)\\ {\xi }_2=d_{ 33}U M_1/\left(M_1+M_2\right)\end{array}$

At U = 75 V, $M_1$  = 1 kg, $M_2$  = 4 kg, $d_{ 33}$ = 4×10^-10 m/V the steady-state nanodisplacements are determined ${\xi }_1$  = 24 nm, ${\xi }_2$  = 6 nm and ${\xi }_1+{\xi }_2$  = 30 nm with error 10%.

The transfer equation of the transverse piezoactuator is determined at one the fixed face and the elastic-inertial load

$W\left(s\right)=\frac{\Xi \left(s\right)}{U\left(s\right)}=\frac{k_{ 31}^E}{T_t^2{s}^2+2T_t{\xi }_{t}s+1}$

$k_{ 31}^E=d_{ 31}\left(h/\delta \right)/\left(1+C_l/C_{ 11}^E\right)$

$T_t=\sqrt{M/\left(C_l+C_{ 11}^E\right)},{\omega }_t=1/T_t$

where $k_{ 31}^E$  is the transfer coefficient, $C_l$ , $C_{ 11}^E$  are the stiffness for the load and the transverse piezoactuator, $T_t,{\xi }_t,{\omega }_t$  are the time constant, the attenuation coefficient, the conjugate frequency.

At $C_l$  = 0.2×10⁷ N/m, $C_{ 11}^E$ = 1.4×10⁷ N/m, $M$  = 2 kg the parameters are obtained $T_t$  = 0.354×10^-3 s, ${\omega }_t$  = 2.8×10³ s^-1 with error 10%.

The steady-state nanodisplacement of the transverse piezoactuator is written for elastic-inertial load

$\Delta h=\frac{d_{ 31}\left(h/\delta \right)U}{1+C_l/C_{ 11}^E}=k_{ 31}^{E}U$

At $h/\delta$  = 20, $C_l/C_{ 11}^E$ = 0.14, $d_{31}$ = 2∙10^-10 m/V the transfer coefficient of the transverse piezoactuator is received $k_{ 31}^E$  = 3.5 nm/V with error 10%.

The structural scheme of a piezoactuator is constructed for astrophysics. The matrix of the nanodisplacement of a piezoactuator is obtained. The characteristics of a piezoactuator are determined.

None.

The Authors declares that there is no Conflict of interest.

1. Schultz J, Ueda J, Asada H. Cellular Actuators. Butterworth-Heinemann Publisher, Oxford; 2017. 382 p.
2. Afonin SM. Absolute stability conditions for a system controlling the deformation of an electromagnetoelastic transducer. Dokl. Math. 2006;74:943–948.
3. Uchino K. Piezoelectric actuator and ultrasonic motors. Boston, MA: Kluwer Academic Publisher; 1997. 350 p.
4. Afonin SM. Generalized parametric structural model of a compound elecromagnetoelastic transduser. Dokl Phys. 2005;50(2):77–82.
5. Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transducer. Dokl Phys. 2008;53(3):137–143.
6. Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Dokl Math. 2006;73(2):307–313.
7. Cady WG. Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. New York, London: McGraw-Hill Book Company; 1946. 806 p.
8. Mason W. Physical Acoustics: Principles and Methods. Vol.1. Part A. Methods and Devices. New York: Academic Press; 1964. 515p.
9. Yang Y, Tang L. Equivalent Circuit Modeling of Piezoelectric Energy Harvesters. J Int Mat Sys Str. 2009;20(18):2223–2235.
10. Zwillinger D. Handbook of Differential Equations. Boston: Academic Press; 1989. 673 p.
11. Afonin SM. A generalized structural-parametric model of an elecromagnetoelastic converter for nano- and micrometric movement control systems: III. Transformation parametric structural circuits of an elecromagnetoelastic converter for nano- and micrometric movement control systems. J Comput Syst Sci Int. 2006;45(2):317–325.
12. Afonin SM. Generalized structural-parametric model of an electromagnetoelastic converter for control systems of nano-and micrometric movements: IV. Investigation and calculation of characteristics of step-piezodrive of nano-and micrometric movements. J. Comput. Syst Sci Int. 2006;45(6):1006–1013.
13. Afonin SM. Decision wave equation and block diagram of electromagnetoelastic actuator nano- and micro displacement for communications systems. Int J Inf Com Sci. 2016;1(2):22–29.
14. Afonin SM. Structural-parametric model and transfer functions of electroelastic actuator for nano- and micro displacement. Chapter 9 in Piezoelectric and Nanomaterials: Fundamentals, Developments and Applications. Parinov IA, editor. New York: Nova Science; 2015. p. 225–242.
15. Afonin SM. A structural-parametric model of electroelastic actuator for nano- and micro displacement of mechatronic system. Chapter 8 in Advances in Nanotechnology. Bartul Z, Trenor J, editors. New York: Nova Science; 2017. p. 259–284.
16. Afonin SM. Electromagnetoelastic nano- and microactuators for mechatronic systems. Russ. Engin. Res. 2018;38(12):938–944.
17. Afonin SM. Nano- and micro-scale piezomotors. Russ Engin Res. 2012;32(7-8):519–522.
18. Afonin SM. Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers. Mech Solids. 2007;42(1):43–49.
19. Afonin SM. Stability of strain control systems of nano-and micro displacement piezotransducers. Mech Solids. 2014;49(2):196–207.
20. Afonin SM. Structural-parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. Int J Physics. 2017;5(1):9–15.
21. Afonin SM. Structural-parametric model multilayer electromagnetoelastic actuator for nanomechatronics. Int J Physics. 2019;7(2):50–57.
22. Afonin SM. Calculation deformation of an engine for nano biomedical research. Int J Bio Res. 2021;1(5):1–4.
23. Afonin SM. Precision engine for nanobiomedical research. Bio Res Clinical Rev. 2021;3(4):1–5.
24. Afonin SM. Solution wave equation and parametric structural schematic diagrams of electromagnetoelastic actuators nano- and micro displacement. Int J Math Ana App. 2016;3(4):31–38.
25. Afonin SM. Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 2018;7(1):1–9.
26. Afonin SM. Structural-parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 2019;8(3):1–14.
27. Afonin SM. Structural-parametric models and transfer functions of electromagnetoelastic actuators nano- and micro displacement for mechatronic systems. Int J Theo App Math. 2016;2(2):52–59.
28. Afonin SM. Design static and dynamic characteristics of piezoelectric nanomicro transducers. Mech. Solids. 45(1):123–132.
29. Afonin SM. Electromagnetoelastic Actuator for Nanomechanics. Mech Eng. 2018;18(2):19–23.
30. Afonin SM. Multilayer electromagnetoelastic actuator for robotics systems of nanotechnology. 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus). 2018;1698–1701.
31. Afonin SM. A block diagram of electromagnetoelastic actuator nanodisplacement for communications systems. Tran Net Com. 2018;6(3):1–9.
32. Afonin SM. Decision matrix equation and block diagram of multilayer electromagnetoelastic actuator micro and nanodisplacement for communications systems. Tran Net Com. 2019;7(3):11–21.
33. Afonin SM. Condition absolute stability control system of electromagnetoelastic actuator for communication equipment. Tran Net Com. 2020;8(1):8–15.
34. Afonin SM. A Block diagram of electromagnetoelastic actuator for control systems in nanoscience and nanotechnology. Tran Mach Learn Art Int. 2020;8(4):23–33.
35. Afonin SM. Optimal control of a multilayer electroelastic engine with a longitudinal piezoeffect for nanomechatronics systems. ASI. 2020;3(4):1–7.
36. Afonin SM. Coded сontrol of a sectional electroelastic engine for nanomechatronics systems. ASI. 2021;4(3):1–11.
37. Afonin SM. Structural scheme actuator for nano research. COJ Rev Res. 2020;2(5):1–3.
38. Afonin SM. Structural–parametric model electroelastic actuator nano and micro displacement of mechatronics systems for nanotechnology and ecology research. MOJ Eco Environ Sci. 2018;3(5):306‒309.
39. Afonin SM. Electromagnetoelastic actuator for large telescopes. Aeron Aero Open Access J. 2018;2(5):270–272.
40. Afonin SM. Condition absolute stability of control system with electro elastic actuator for nano bioengineering and microsurgery. Sur Case Studies Open Access J. 2019;3(3):307–309.
41. Afonin SM. Piezo actuators for nanomedicine research. MOJ App Bio Biomech. 2019;3(2):56–57.
42. Afonin SM. Frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics. MOJ App Bio Biomech. 2019;3(6):137–140.
43. Afonin SM. Multilayer piezo engine for nanomedicine research. MOJ App Bio Biomech. 2020;4(2):30–31.
44. Afonin SM. Structural scheme of electromagnetoelastic actuator for nano biomechanics. MOJ App Bio Biomech. 2021;5(2):36–39.
45. Afonin SM. Multilayer engine for microsurgery and nano biomedicine. Sur Case Studies Open Access J. 2020;4(4): 423–425.
46. Afonin SM. A structural-parametric model of a multilayer electroelastic actuator for mechatronics and nanotechnology. Chapter 7 in Advances in Nanotechnology. Bartul Z, Trenor J, editors. New York: Nova Science; 2019. p. 169–186.
47. Afonin SM. Electroelastic digital-to-analog converter actuator nano and micro displacement for nanotechnology. Chapter 6 in Advances in Nanotechnology. Bartul Z, Trenor J, editors. New York: Nova Science; 2020. p. 205–218.
48. Afonin SM. Characteristics of an electroelastic actuator nano- and micro displacement for nanotechnology. Chapter 8 in Advances in Nanotechnology. Bartul Z, Trenor J, editors. New York: Nova Science; 2021. p. 251–266.
49. Afonin SM. An absolute stability of nanomechatronics system with electroelastic actuator. Chapter 9 in Advances in Nanotechnology. In: Bartul Z, Trenor J, editors. New York: Nova Science; 2022. p. 183–198.
50. Afonin SM. Rigidity of a multilayer piezoelectric actuator for the nano and micro range. Rus Eng Res. 2021;41(4): 285–288.
51. Encyclopedia of Nanoscience and Nanotechnology. Nalwa HS, editor. Los Angeles: American Scientific Publishers; 2004.
52. Springer Handbook of Nanotechnology. Bhushan B, editor. New York: Springer; 2004. 1222 p.