Condition absolute stability of system with nano piezoactuator for astrophysics research

doi:10.15406/aaoaj.2023.07.00176

eISSN: 2576-4500

Aeronautics and Aerospace Open Access Journal

Short Communication Volume 7 Issue 3

Condition absolute stability of system with nano piezoactuator for astrophysics research

Afonin SM

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

National Research University of Electronic Technology, Russia

Correspondence: Afonin SM, National Research University of Electronic Technology MIET, Moscow, Russia

Received: June 19, 2023 | Published: July 5, 2023

Citation: Afonin SM. Condition absolute stability of system with nano piezoactuator for astrophysics research. Aeron Aero Open Access J. 2023;7(3):99-102. DOI: 10.15406/aaoaj.2023.07.00176

Download PDF

Abstract

For the nano piezoactuator with hysteresis in control system its set of equilibrium positions is the segment of line. By applying Yakubovich criterion for system with the nano piezoactuator the condition absolute stability of system is evaluated.

Keywords: condition absolute stability, control system, nano piezoactuator, hysteresis, set equilibrium positions

Introduction

The nano piezoactuator is used in astrophysics, astronomy, nanotechnology, nanomechanics, adaptive optics for alignment, compensation deformation, image stabilization, autofocus.^1–15 The nano piezoactuator is the piezomechanical device that transforms electrical signals into mechanical nano movement and force and is applied to actuate mechanisms, systems, or management based on the piezoeffect. The nano piezoactuator works on the basis of the inverse piezoeffect due to its nano deformation at the electric field strength is applied.^16–34 On the characteristic of the nano piezoactuator deformation from the electric field strength, the initial curve is observed, on which the vertices of the main hysteresis loops lie. The main hysteresis loops have a symmetric change in the electric field strength relative to zero, and partial loops have an asymmetric change in the strength relative to zero.^{2–4,35–59}

For calculation absolute stability of system with the nano piezoactuator is applied Yakubovich criterion.^3–35 Many equilibrium positions are found in system with nano piezoactuator for astrophysics.

Condition absolute stability of system

Yakubovich's criterion of absolute stability is development for Popov's criterion of absolute stability. Measurements of the deformations for the nano longitudinal piezoactuator were carried out by the electronic measuring system Model 214 of Calibre plant. The experimental static hysteresis characteristic of the deformation of the nano longitudinal piezoactuator made of ceramic PZT is shown on Figure 1 with the main hysteresis loop and with the partial hysteresis loop.

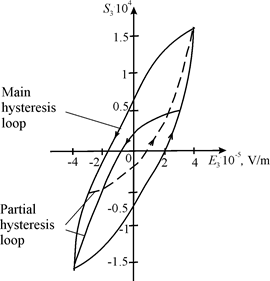
Figure 1 Hysteresis characteristic of nano longitudinal piezoactuator.

For written the hysteresis of the nano piezoactuator the Preisach model is used for its hysteresis deformation. The hysteresis function of the relative deformation the nano piezoactuator on Figure 1 is determined^3,35–52

$S_{i} = F {[{E_{m} |}_{0}^{t}, t, S_{i} (0), sign {\dot{E}}_{m}]}_{}^{}$

here $S_{i}$ - the hysteresis deformation, t - time, $S_{i} (0)$ - the initial condition, $E_{m}$ - the strength of electric field and $sign {\dot{E}}_{m}$ - the sign for velocity of change strength.

In control system the set of equilibrium positions is the set of points M of intersection of the line L with the hysteresis characteristic on Figure 2 in the form of the selected line segment. The equation of the line L is evaluated

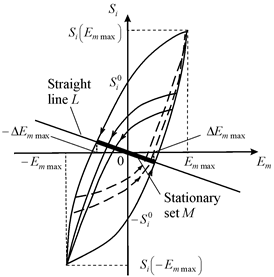
Figure 2 Hysteresis characteristic of nano piezoactuator.

$E_{m} + k S_{i} = 0$

here $k$ - the transfer coefficient for the linear part of system.

The expression for the symmetric main hysteresis loop of the nano piezoactuator on Figure 2 is determined

$S_{i} = d_{m i} E_{m} - γ_{m i} E_{m max} {(1 - \frac{E_{m}^{2}}{E_{m max}^{2}})}^{n_{m i}} sign {\dot{E}}_{m}$

here $d_{m i}$ - the piezomodule, $γ_{m i} = S_{i}^{0} / E_{m max}$ - the coefficient of hysteresis, $S_{i}^{0}$ - the relative deformation at $E_{m} = 0$ , $n_{m i}$ - the coefficient and for PZT $n_{m i}$ = 1.

The width of the resting zone at $Δ E_{m max}$ is determined

$Δ E_{m max} + k S_{i}^{+} (Δ E_{m max}) = 0$

here $Δ$ - the relative value of electric field strength; $S_{i}^{+} (Δ E_{m max})$ - the value of the relative deformation on the ascending branch for ${\dot{E}}_{m} > 0$ , $S_{i}^{-} (- Δ E_{m max})$ - the value of the relative deformation on the descending branch for ${\dot{E}}_{m} < 0$ on Figure 2.

For the symmetric main hysteresis loop the equation is evaluated

$S_{i}^{+} (Δ E_{m max}) = d_{m i} Δ E_{m max} - γ_{m i} E_{m max} (1 - \frac{{(Δ E_{m max})}^{2}}{E_{m max}^{2}})$

After transformation the expression determined

$S_{i}^{+} (Δ E_{m max}) = d_{m i} Δ E_{m max} - γ_{m i} E_{m max} (1 - Δ^{2})$

From the straight line equation the expression is calculated

$Δ E_{m max} + k E_{m max} {[d_{m i} Δ - γ_{m i} (1 - Δ^{2})]}_{}^{} = 0$

Therefore, the equation is determined

$Δ + k {[d_{m i} Δ - γ_{m i} (1 - Δ^{2})]}_{}^{} = 0$

The quadratic equation is calculated

$Δ^{2} + \frac{(1 + k d_{m i})}{k γ_{m i}} Δ - 1 = 0$

The relative width of the rest zone $2 Δ$ of system with nano piezoactuator is obtained

$2 Δ = - \frac{(1 + k d_{m i})}{k γ_{m i}} + \sqrt{\frac{{(1 + k d_{m i})}^{2}}{k^{2} γ_{m i}^{2}} + 4}$

The minimum value $ν_{1 m i}$ and maximum value $ν_{2 m i}$ of the tangent the angle of inclination to the hysteresis of the nano piezoactuator are obtained in the form

$ν_{1 m i}, ν_{2 m i} \in [0, ν_{m i}]$

$ν_{m i} = max [d S_{i} / d E_{m}]$

The values $ν_{1 m i}$ and $ν_{2 m i}$ are determined for the hysteresis characteristic at the maximum strength in the nano piezoactuator.

The ratio of the piezomodules of the nano piezoactuator with transverse, longitudinal, shear piezoelectric effects is proportional the ratio of its tangents of the angle of inclination to the hysteresis

$d_{3 1} : d_{3 3} : d_{1 5} = ν_{3 1} : ν_{3 3} : ν_{1 5}$

From the Yakubovich criterion^35,52 the absolute stability of system with nano piezoactuator for astrophysics research is obtained. The condition absolute stability of system with nano piezoactuator on Figure 3 at $ν_{1 m i} = 0$ and $ν_{2 m i} = ν_{m i}$ is evaluated

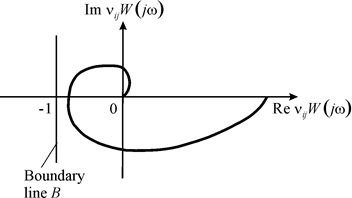
Figure 3 Condition absolute stability of system with nano piezoactuator.

$Re ν_{m i} W (j ω) \geq - 1$

here ω - the frequency, j - the imaginary unit. On Figure 3 shows the amplitude-phase frequency characteristic for the frequency transfer function $W (j ω)$ with boundary vertical line B, passing through -1 on the real axis.

For the nano transverse or longitudinal piezoactuator from PZT the experimental maximum tangent at transverse piezoeffect $ν_{3 1}$ = 0.6 nm/V or at longitudinal piezoeffect $ν_{3 3}$ = 1 nm/V are obtained.

For the condition absolute stable Lyapunov control system the Yakubovich absolute stability criterion have the visual and simple representation of the results for the system stability.

Conclusion

By using Yakubovich criterion for system with the nano piezoactuator the condition absolute stability of system is evaluated for astrophysics research. For the nano piezoactuator with hysteresis in control system for astrophysics research the set of equilibrium positions is the segment of line.