In the work is calculated of the piezoactuator for astrophysics. The structural scheme of the piezoactuator is determined for astrophysics. The matrix equation is constructed for the piezoactuator. The mechanical characteristic is determined. The parameters of the piezoactuator are obtained in nano control systems for astrophysics.

Keywords: Piezoactuator, Structural scheme, Astrophysics

The piezoactuator is used for astrophysics.^1-43 In nanotechnology and precision machining the piezoactuator is widely used.^17-19,58 The piezoactuator is applied for the nano alignment in adaptive optics and interferometers.^4-59

The method mathematical physics is using for calculation the structural scheme of piezoactuator in nano control systems for astrophysics.

Structural scheme of piezoactuator

The structural scheme of the piezoactuator for astrophysics is calculated by the method mathematical physics by using the equations of the inverse and direct piezoeffects and the decision of the second order ordinary differential equation for the piezoactuator. From the structural model and scheme we have the matrix equation and the mechanical characteristic the nano piezoactuator, and its parameters in adaptive optics for astrophysics.

Let us construct of structural models of piezoactuators. The expression of the inverse piezoeffect.^1-15

$S_i=d_{mi}{E}_m+s_{ij}^E{T}_j$

here $S_i$ , $d_{mi}$ , $E_m$ , $s_{ij}^E$ , $T_j$ , are the relative displacement, piezomodule, strength electric field, elastic compliance, strength mechanical field.

The expression of the longitudinal inverse piezoeffect has the form.^1-15

$S_3=d_{33}{E}_3+s_{33}^E{T}_3$

The second order ordinary differential equation of the piezoactuator is used.^4-54

$\frac{d^2\Xi \left(x,s\right)}{d{x}^2}-{\gamma }^2\Xi \left(x,s\right)=0$

here $\Xi \left(x,s\right)$ , s, x, γ are the Laplace transform of the displacement, the parameter, the coordinate, the coefficient of propagation. For the longitudinal piezoactuator we have at $x=0$  the deformation $\Xi \left(0,s\right)={\Xi }_1\left(s\right)$  and at $x=\delta$   $\Xi \left(\delta ,s\right)={\Xi }_2\left(s\right)$ . The decision is calculated.

$\Xi \left(x,s\right)=\left\{{\Xi }_1\left(s\right)\text{sh}\left[\left(\delta -x\right)\gamma \right]+{\Xi }_2\left(s\right)\text{sh}\left(x\gamma \right)\right\}/\text{sh}\left(\delta \gamma \right)$

From the expression of the longitudinal inverse piezoeffect and and two boundary conditions we have the set of equations.^4-32

$T_3\left(0,s\right)=\frac{1}{s_{33}^E}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=0}-\frac{d_{33}}{s_{33}^E}{E}_3\left(s\right)$

$T_3\left(\delta ,s\right)=\frac{1}{s_{33}^E}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=\delta }-\frac{d_{33}}{s_{33}^E}{E}_3\left(s\right)$

After using the decision of the differential equation of the we have the structural model of the longitudinal piezoactuator.

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_1\left(s\right)+{\left({\chi }_{33}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{33}{E}_3\left(s\right)-\left[\gamma /\text{sh}\left(\delta \gamma \right)\right]\\ \times \left[\text{ch}\left(\delta \gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_2\left(s\right)+{\left({\chi }_{33}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{33}{E}_3\left(s\right)-\left[\gamma /\text{sh}\left(\delta \gamma \right)\right]\\ \times \left[\text{ch}\left(\delta \gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\chi }_{33}^E=s_{33}^E/S_0$

here ${\Xi }_1\left(s\right)$ , ${\Xi }_2\left(s\right)$  are the Laplace transforms of the displacements, $S_0$  is the area.

The expression of the transverse inverse inverse piezoeffect has the form^1-15

$S_1=d_{31}{E}_3+s_{11}^E{T}_1$

The decision of the differential equation is written.

$\Xi \left(x,s\right)=\left\{{\Xi }_1\left(s\right)\text{sh}\left[\left(h-x\right)\gamma \right]+{\Xi }_2\left(s\right)\text{sh}\left(x\gamma \right)\right\}/\text{sh}\left(h\gamma \right)$

From the expression of the transverse inverse piezoeffect and two boundary conditions we have the set of equations.

$T_1\left(0,s\right)=\frac{1}{s_{11}^E}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=0}-\frac{d_{31}}{s_{11}^E}{E}_3\left(s\right)$

$T_1\left(h,s\right)=\frac{1}{s_{11}^E}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=h}-\frac{d_{31}}{s_{11}^E}{E}_3\left(s\right)$

By using the decision of the differential equation of the we have the structural model of the transverse piezoactuator.

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_1\left(s\right)+{\left({\chi }_{11}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{31}{E}_3\left(s\right)-\left[\gamma /\text{sh}\left(h\gamma \right)\right]\\ \times \left[\text{ch}\left(h\gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_2\left(s\right)+{\left({\chi }_{11}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{31}{E}_3\left(s\right)-\left[\gamma /\text{sh}\left(h\gamma \right)\right]\\ \times \left[\text{ch}\left(h\gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\chi }_{11}^E=s_{11}^E/S_0$

The expression of the shift inverse inverse piezoeffect has the form.^1-15

$S_5=d_{15}{E}_1+s_{55}^E{T}_5$

The decision of the differential equation has the form.

$\Xi \left(x,s\right)=\left\{{\Xi }_1\left(s\right)\text{sh}\left[\left(b-x\right)\gamma \right]+{\Xi }_2\left(s\right)\text{sh}\left(x\gamma \right)\right\}/\text{sh}\left(b\gamma \right)$

From the expression of the shift inverse piezoeffect and two boundary conditions we have the set of equations.

$T_5\left(0,s\right)=\frac{1}{s_{55}^E}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=0}-\frac{d_{15}}{s_{55}^E}{E}_1\left(s\right)$

$T_5\left(b,s\right)=\frac{1}{s_{55}^E}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=b}-\frac{d_{15}}{s_{55}^E}{E}_1\left(s\right)$

By using the decision of the differential equation we have the structural model of the shift piezoactuator.

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_1\left(s\right)+{\left({\chi }_{55}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{15}{E}_1\left(s\right)-\left[\gamma /\text{sh}\left(b\gamma \right)\right]\\ \times \left[\text{ch}\left(b\gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_2\left(s\right)+{\left({\chi }_{55}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{15}{E}_1\left(s\right)-\left[\gamma /\text{sh}\left(b\gamma \right)\right]\\ \times \left[\text{ch}\left(b\gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\chi }_{55}^E=s_{55}^E/S_0$

At $l=\{\delta ,h,b$  the decision in general of the differential equation of the piezoactuator has the form.

$\Xi \left(x,s\right)=\left\{{\Xi }_1\left(s\right)\text{sh}\left[\left(l-x\right)\gamma \right]+{\Xi }_2\left(s\right)\text{sh}\left(x\gamma \right)\right\}/\text{sh}\left(l\gamma \right)$

From the expression of the inverse piezoeffect and two boundary conditions we have the set of equations.

$T_j\left(0,s\right)=\frac{1}{s_{ij}^{\Psi }}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=0}-\frac{{\nu }_{mi}}{s_{ij}^{\Psi }}{\Psi }_m\left(s\right)$

$T_j\left(l,s\right)=\frac{1}{s_{ij}^{\Psi }}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=l}-\frac{{\nu }_{mi}}{s_{ij}^{\Psi }}{\Psi }_m\left(s\right)$

By using the decision in general of the second order ordinary differential equation the structural model in general of the nano piezoactuator is calculated on Figure 1.

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_1\left(s\right)+{\left({\chi }_{ij}^{\Psi }\right)}^{-1}\\ \times \left[\begin{array}{l}{\nu }_{mi}{\Psi }_m\left(s\right)-\left[\gamma /\text{sh}\left(l\gamma \right)\right]\\ \times \left[\text{ch}\left(l\gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_2\left(s\right)+{\left({\chi }_{ij}^{\Psi }\right)}^{-1}\\ \times \left[\begin{array}{l}{\nu }_{mi}{\Psi }_m\left(s\right)-\left[\gamma /\text{sh}\left(l\gamma \right)\right]\\ \times \left[\text{ch}\left(l\gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\chi }_{ij}^{\Psi }=s_{ij}^{\Psi }/S_0$

here

$v_{mi}=\{\begin{array}{c}{d}_{33},d_{31},d_{15}\\ g_{33},g_{31},g_{15}\end{array}$

${\Psi }_m==\{\begin{array}{c}{E}_3,E_1\\ D_3,D_1\end{array}$

$s_{ij}^{\Psi }==\{\begin{array}{c}{s}_{33}^E,s_{11}^E,s_{55}^E\\ s_{33}^D,s_{11}^D,s_{55}^D\end{array}$

$\gamma =\{{\gamma }^E,{\gamma }^D$

$c^{\Psi }=\{c^E,c^D$

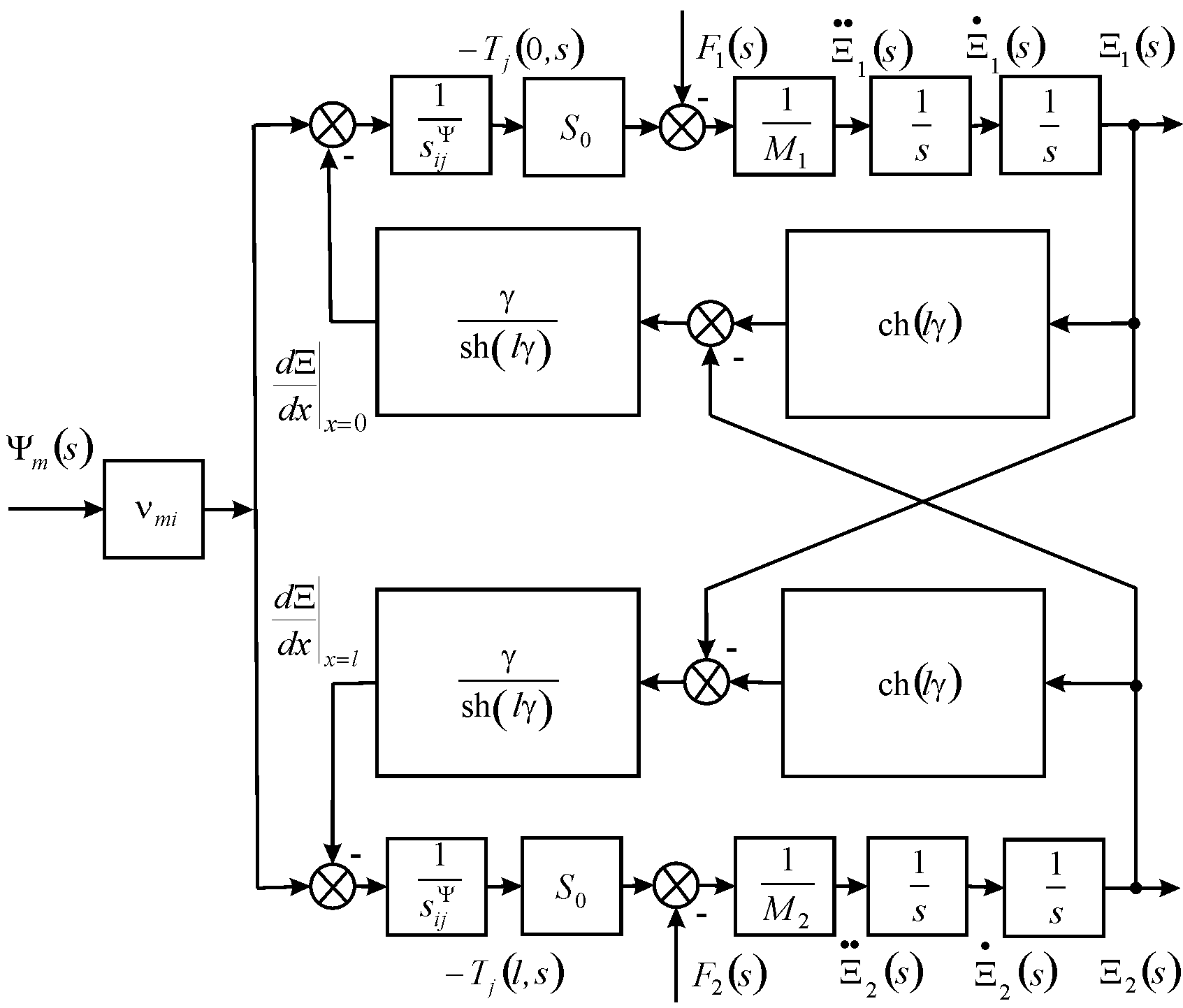
Figure 1 Structural scheme in general of nano piezoactuator.

The matrix for the deformations of the piezoactuator from the structural model and scheme on Figure 1 is calculated.

$\left(\begin{array}{c}{\Xi }_1\left(s\right)\\ {\Xi }_2\left(s\right)\end{array}\right)=\left(\begin{array}{c}\begin{array}{ccc}{W}_{11}\left(s\right)& W_{12}\left(s\right)& W_{13}\left(s\right)\end{array}\\ \begin{array}{ccc}{W}_{21}\left(s\right)& W_{22}\left(s\right)& W_{23}\left(s\right)\end{array}\end{array}\right)\left(\begin{array}{c}{\Psi }_m\left(s\right)\\ F_1\left(s\right)\\ F_2\left(s\right)\end{array}\right)$

$W_{11}\left(s\right)={\Xi }_1\left(s\right)/{\Psi }_m\left(s\right)={{\nu }_{mi}{}_{}^{}\left[M_2{\chi }_{ij}^{\Psi }{s}^2+\gamma \text{th}\left(l\gamma /2\right)\right]/A}_{ij}$

$\begin{array}{l}{A}_{ij}=M_1{M}_2{\left({\chi }_{ij}^{\Psi }\right)}^2{s}^4+\left\{\left(M_1+M_2\right){\chi }_{ij}^{\Psi }/{\left[c^{\Psi }\text{th}\left(l\gamma \right)\right]}^{}\right\}{s}^3+\\ +\left[\left(M_1+M_2\right){\chi }_{ij}^{\Psi }\alpha /\text{th}\left(l\gamma \right)+1/{\left(c^{\Psi }\right)}^2\right]s^2+2\alpha s/c^{\Psi }+{\alpha }^2\end{array}$

$W_{21}\left(s\right)={\Xi }_2\left(s\right)/{\Psi }_m\left(s\right)={{\nu }_{mi}{}_{}^{}{\left[M_1{\chi }_{ij}^{\Psi }{s}^2+\gamma \text{th}\left(l\gamma /2\right)\right]}^{}/A}_{ij}$

$W_{12}\left(s\right)={\Xi }_1\left(s\right)/F_1\left(s\right)=-{{\chi }_{ij}^{\Psi }{}_{}^{}\left[M_2{\chi }_{ij}^{\Psi }{s}^2+\gamma /\text{th}\left(l\gamma \right)\right]/A}_{ij}$

$\begin{array}{l}{W}_{13}\left(s\right)={\Xi }_1\left(s\right)/F_2\left(s\right)=\\ =W_{22}\left(s\right)={\Xi }_2\left(s\right)/F_1\left(s\right)={\left[{\chi }_{ij}^{\Psi }\gamma /\text{sh}\left(l\gamma \right)\right]/A}_{ij}\end{array}$

$W_{23}\left(s\right)={\Xi }_2\left(s\right)/F_2\left(s\right)=-{{\chi }_{ij}^{\Psi }{}_{}^{}\left[M_1{\chi }_{ij}^{\Psi }{s}^2+\gamma /\text{th}\left(l\gamma \right)\right]/A}_{ij}$

The longitudinal deformations are obtained.

${\xi }_1=d_{33}U{M}_2/\left(M_1+M_2\right)$

${\xi }_2=d_{33}U{M}_1/\left(M_1+M_2\right)$

For $d_{33}$  = 4×10^-10 m/V, U = 50 V, $M_1$  = 1 kg, $M_2$  = 4 kg we have ${\xi }_1$  = 16 nm, ${\xi }_2$  = 4 nm and ${\xi }_1+{\xi }_2$  = 20 nm with error 10%.

Let us evaluate the influence of the anti electromotive force on the deformation of the piezoactuator. The expression of the direct piezoeffect^1-15 is used

$D_m=d_{mi}{T}_i+{\epsilon }_{mk}^E{E}_k$

where $D_m$ , ${\epsilon }_{mk}^E$  are the electric induction and the permittivity,

The direct coefficient of the piezoactuator is written for calculation the voltage negative feedback from anti electromotive force.

$k_d=\frac{d_{mi}{S}_0}{\delta s_{ij}^E}$

The expression of the voltage negative feedback from anti electromotive force on Figure 2 is used.

$U_d\left(s\right)=\frac{d_{mi}{S}_{0}R}{\delta s_{ij}^E}{\stackrel{•}{\Xi }}_{{}_n}\left(s\right)=k_{d}R{\stackrel{•}{\Xi }}_{{}_n}\left(s\right)$ ,  $n=1,2$

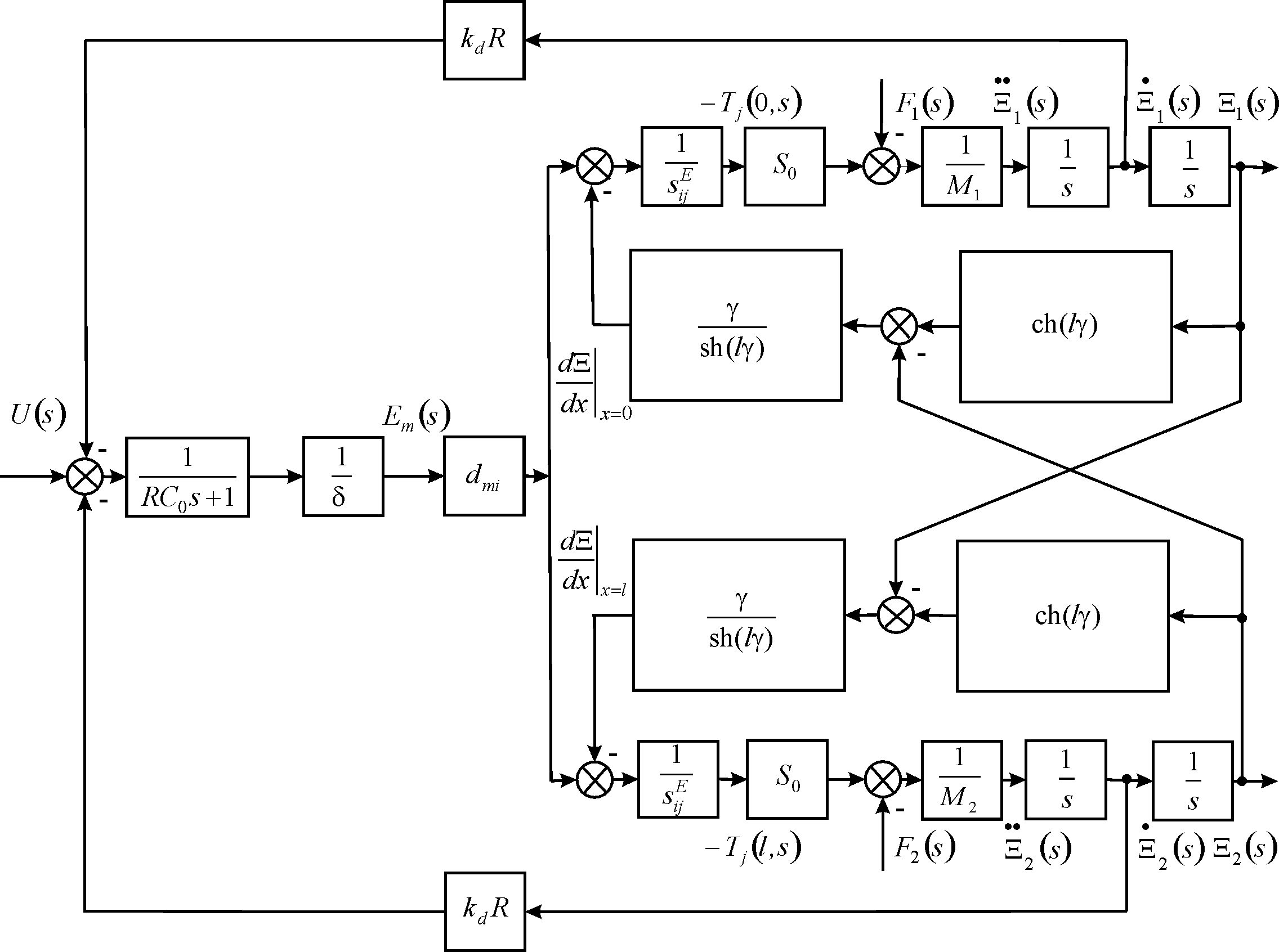
Figure 2 Structural scheme of piezoactuator with negative feedback from anti electromotive force.

The maximum the strength mechanical field and the force in the static working regime have the form at voltage control.

$T_{j\text{max}}=E_m{d}_{mi}/s_{ij}^E$

$F_{\text{max}}=E_m{d}_{mi}{S}_0/s_{ij}^E$

The maximum force in the static working regime has the form at current control.

$F_{\text{max}}=\frac{U}{\delta }{d}_{mi}\frac{S_0}{s_{ij}^E}+\frac{F_{\text{max}}}{S_0}{d}_{mi}{S}_c\frac{1}{{\epsilon }_{mk}^T{S}_c/\delta }\frac{1}{\delta }{d}_{mi}\frac{S_0}{s_{ij}^E}$

$\frac{F_{\text{max}}}{S_0}\left(1-\frac{d_{mi}^2}{{\epsilon }_{mk}^T{s}_{ij}^E}\right)s_{ij}^E=E_m{d}_{mi}$

$T_{j\text{max}}\left(1-k_{mi}^2\right)s_{ij}^E=E_m{d}_{mi}$

$k_{mi}=d_{mi}/\sqrt{s_{ij}^E{\epsilon }_{mk}^T}$

here $k_{mi}$  is the coefficient of electromechanical coupling.

The expressions for the strength mechanical field and the maximum force in the static working regime we have at current control.

$T_{j\text{max}}=E_m{d}_{mi}/s_{ij}^D$

$F_{\text{max}}=E_m{d}_{mi}{S}_0/s_{ij}^D$

$s_{ij}^D=\left(1-k_{mi}^2\right)s_{ij}^E$

The mechanical characteristic of the piezoactuator is determined in the static working regime.

${S_i\left(T_j\right)|}_{\Psi =\text{const}}={{\nu }_{mi}{\Psi }_m|}_{\Psi =\text{const}}+s_{ij}^{\Psi }{T}_j$

The adjustment characteristic of the piezoactuator is calculated in the static working regime.

${S_i\left({\Psi }_m\right)|}_{T=\text{const}}={\nu }_{mi}{\Psi }_m+{s_{ij}^{\Psi }{T}_j|}_{T=\text{const}}$

The mechanical characteristic of the piezoactuator has the form.

$\Delta l=\Delta l_{\text{max}}\left(1-F/F_{\text{max}}\right)$

$\Delta l_{\text{max}}={\nu }_{mi}{\Psi }_{m}l$

$F_{\text{max}}=T_{j\text{ max}}{S}_0={\nu }_{mi}{\Psi }_m{S}_0/s_{ij}^{\Psi }$

The expression of the mechanical characteristic for the transverse piezoactuator is determined

$\Delta h=\Delta h_{\text{max}}\left(1-F/F_{\text{max}}\right)$

$\Delta h_{\text{max}}=d_{31}{E}_{3}h$

$F_{\text{max}}=d_{31}{E}_3{S}_0/s_{11}^E$

At $d_{31}$  = 2∙10^-10 m/V, $E_3$  = 0.25∙10⁵ V/m, h = 2.5∙10^-2 m, $S_0$  = 1.5∙10^-5 m², $s_{11}^E$  = 15∙10^-12 m²/N we have the parameters of the transverse piezoactuator $\Delta h_{\text{max}}$  = 125 nm, $F_{\text{max}}$  = 5 N with error 10%

The deformation of the piezoactuator is obtained at voltage control and elastic load.

$\frac{\Delta l}{l}=d_{mi}{E}_m-\frac{s_{ij}^E}{S_0}F$ , $F=C_e\Delta l$

The adjustment characteristic has the form.

$\Delta l=\frac{d_{mi}l{E}_m}{1+C_e/C_{ij}^E}$

The coefficients of the piezoactuator in general are calculated for the structural scheme of the piezoactuator with negative feedback from anti electromotive force.

$k_d=k_r=\frac{d_{mi}{S}_0}{\delta s_{ij}}$

$s_{ij}=k_s{s}_{ij}^E$

$\left(1-k_{mi}^2\right)\le k_s\le 1$

At one fixed face and elastic-inertial load of the piezoactuator Figure 2 is transformed to Figure 3.

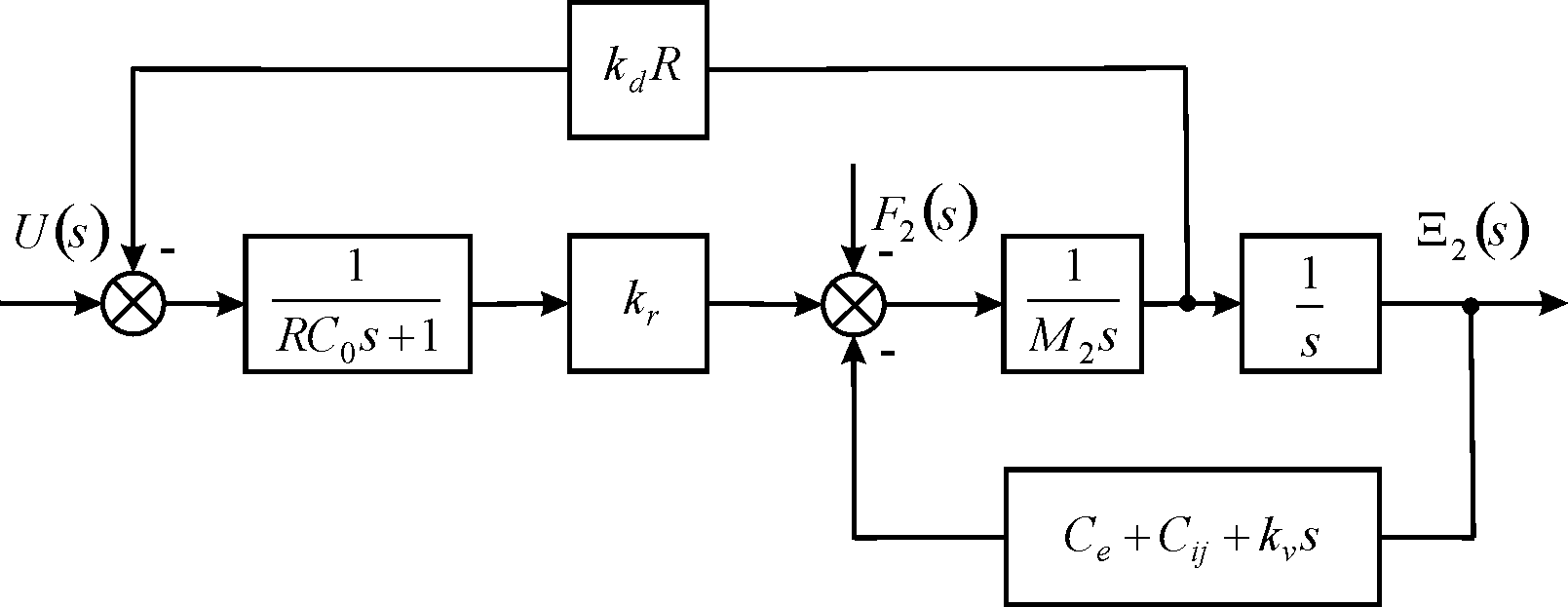
Figure 3 Structural scheme of piezoactuator with negative feedback from anti electromotive force.

At $R=0$  we have the expressions for the transverse piezoactuator at voltage control.

$W\left(s\right)=\frac{\Xi \left(s\right)}{U\left(s\right)}=\frac{k_{31}^U}{T_t^2{s}^2+2T_t{\xi }_{t}s+1}$

$k_{31}^U=d_{31}\left(h/\delta \right)/\left(1+C_e/C_{11}^E\right)$

$T_t=\sqrt{M/\left(C_e+C_{11}^E\right)}$ ,  ${\omega }_t=1/T_t$

At M = 4 kg, $C_e$  = 0.1×10⁷ N/m, $C_{11}^E$  = 1.5×10⁷ N/m the parameters of the transverse piezoactuator are calculated $T_t$  = 0.5×10^-3 s, ${\omega }_t$  = 2×10³ s^-1 with error 10%.

The transverse deformation at voltage control has the form.

$\Delta h=\frac{d_{31}\left(h/\delta \right)U}{1+C_e/C_{11}^E}=k_{31}^{U}U$

At $d_{31}$  = 2∙10^-10 m/V, $h/\delta$  = 22, $C_e/C_{11}^E$  = 0 we have the parameter of the transverse piezoactuator $k_{31}^U$  = 4 nm/V with error 10%.

The structural schemes of the piezoactuator for astrophysics are obtained by the method mathematical physics with using the equations of the inverse and direct piezoeffects and the decision of the second order ordinary differential equation of the piezoactuator. The matrix equation and the mechanical characteristic the nano piezoactuator are determined. The parameters of piezoactuator in adaptive optics for astrophysics are obtained.

The nano piezoactuator is calculated for nano control systems in adaptive optics for astrophysics. The structural schemes of the nano piezoactuator with electrical and mechanical parameters are calculated for astrophysics. In various working regimes the deformation of the nano piezoactuator is determined. The structural schemes of the piezoactuator are obtained. The matrix of the deformations of the piezoactuator is obtained. The parameters of the piezoactuator are determined for astrophysics.

None.

None.

1. Uchino K. Piezoelectric actuator and ultrasonic motors. Elect Mat Sci Technol. 1977;1:350.
2. Afonin SM. Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Doklady Math. 2006;74(3):943–948.
3. Liu Y, Zhang S, Yan P, et al. Finite element modeling and test of piezo disk with local ring electrodes for micro displacement. Micromachines. 2022;13(6):951.
4. Afonin SM. Generalized parametric structural model of a compound elecromagnetoelastic transduser. Doklady Physics. 2005;50(2):77–82.
5. Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transducer. Doklady Physics. 2008;53(3):137–143.
6. Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady Math. 2006;73(2):307–313.
7. Cady WG. Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. McGraw–Hill Book Company, New York, London. 1946;806.
8. Mason W. Physical Acoustics: Principles and Methods. Methods and Devices. Academic Press, New York. 1964;1:515.
9. Yang Y, Tang L. Equivalent circuit modeling of piezoelectric energy harvesters. J Intelligent Mat Sys Struc. 2019;20(18):2223–2235.
10. Zwillinger D. Handbook of differential equations. Academic Press, Boston. 1989;673.
11. Afonin SM. A generalized structural–parametric model of an elecromagnetoelastic converter for nano– and micrometric movement control systems: III. Transformation parametric structural circuits of an elecromagnetoelastic converter for nano– and micrometric movement control systems. J Comput Sys Sci Int. 2006;45(6):1006–1013.
12. Afonin SM. Generalized structural–parametric model of an electromagnetoelastic converter for control systems of nano– and micrometric movements: IV. Investigation and calculation of characteristics of step–piezodrive of nano–and micrometric movements. J Comput Sys Sci Int. 2006;45(6):1006–1013.
13. Afonin SM. Decision wave equation and block diagram of electromagnetoelastic actuator nano– and microdisplacement for communications systems. Int J Info Comm Sci. 2016;1(2):22–29.
14. Afonin SM. Structural–parametric model and transfer functions of electroelastic actuator for nano– and microdisplacement. Chapter 9 in Piezoelectrics and nanomaterials: fundamentals, developments and applications. Ed. Parinov IA. Nova Science, New York. 2015;225–242.
15. Afonin SM. A structural–parametric model of electroelastic actuator for nano– and microdisplacement of mechatronic system. Chapter 8 in Advances in Nanotechnology. Bartul Z, Trenor J, Nova Science, New York, 2017;19:259–284.
16. Shevtsov SN, Soloviev AN, Parinov IA, et al. Piezoelectric actuators and generators for energy harvesting. Res Develop. 2018;182.
17. Adaptive Optics – Core Morrow, 2023, Harbin, China.
18. Precision Machining – Core Morrow, 2023. Harbin, China.
19. Baraniuk R, Drossel WG. Simplification of the model of piezoelectric actuator control based on preliminary measurements. Actuators. 2020;9(3):90.
20. Afonin SM. Electromagnetoelastic nano– and microactuators for mechatronic systems. Russian Eng Res. 2018;38(12):938–944.
21. Afonin SM. Nano– and micro–scale piezomotors. Russian Eng Res. 2021;32(7–8):519–522.
22. Afonin SM. Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers. Mechanics of Solids. 2007;42(1):43–49.
23. Afonin SM. Stability of strain control systems of nano–and microdisplacement piezotransducers. Mechanics of Solids. 2014;49(2):196–207.
24. Afonin SM. Structural–parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. Int J Phys. 2017;5(1):9–15.
25. Afonin SM. Structural–parametric model multilayer electromagnetoelastic actuator for nanomechatronics. Int J Phys. 2019;7(2):50–57.
26. Afonin SM. Calculation deformation of an engine for nano biomedical research. Int J Biomed Res. 2021;1(5):1–4.
27. Afonin SM. Precision engine for nanobiomedical research. Biomed Res Clin Rev. 2021;3(4):1–5.
28. Afonin SM. Solution wave equation and parametric structural schematic diagrams of electromagnetoelastic actuators nano– and microdisplacement. Int J Math Analysis Appl. 2016;3(4):31–38.
29. Afonin SM. Structural–parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 2018;7(1):6.
30. Afonin SM. Structural–parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 2019;8(3):52.
31. Afonin SM. Structural–parametric models and transfer functions of electromagnetoelastic actuators nano– and microdisplacement for mechatronic systems. Int J Theor Appl Math. 2016;2(2):52–59.
32. Afonin SM. Design static and dynamic characteristics of a piezoelectric nanomicrotransducers. Mechanics of Solids. 2010;45(1):123–132.
33. Afonin SM. Electromagnetoelastic Actuator for Nanomechanics. Global J Res Eng: A Mech Mech Eng. 2018;18(2):19–23.
34. Afonin SM. Multilayer electromagnetoelastic actuator for robotics systems of nanotechnology. Proceedings of the 2018 IEEE Conference EIConRus. 2018;1698–1701.
35. Afonin SM. A block diagram of electromagnetoelastic actuator nanodisplacement for communications systems. Transac Net Commun. 2018;6(3):1–9.
36. Afonin SM. Decision matrix equation and block diagram of multilayer electromagnetoelastic actuator micro and nanodisplacement for communications systems. Transac Net Commun. 2019;7(3):11–21.
37. Afonin SM. Condition absolute stability control system of electromagnetoelastic actuator for communication equipment. Transac Net Commun. 2020;8(1):8–15.
38. Afonin SM. A Block diagram of electromagnetoelastic actuator for control systems in nanoscience and nanotechnology. Transac Machine Learn Artificial Intelligence. 2020;8(4):23–33.
39. Afonin SM. Optimal control of a multilayer electroelastic engine with a longitudinal piezoeffect for nanomechatronics systems. Appl Sys Innovat. 2020;3(4):53.
40. Afonin SM. Coded сontrol of a sectional electroelastic engine for nanomechatronics systems. Appl Sys Innovat. 2020;4(3):47.
41. Afonin SM. Structural–parametric model actuator of adaptive optics for composite telescope and astrophysics equipment. Phys Astron Int J. 2020;4(1):18–21.
42. Afonin SM. An actuator nano and micro displacements for composite telescope in astronomy and physics research. Phys Astron Int J. 2020;4(4):165–167.
43. Afonin SM. Calculation of the deformation of an electromagnetoelastic actuator for composite telescope and astrophysics equipment. Phys Astron Int J. 2021;5(2):55–58.
44. Afonin SM. Structural scheme actuator for nano research. COJ Rev Res. 2020;2(5):1–3.
45. Afonin SM. Structural–parametric model electroelastic actuator nano– and microdisplacement of mechatronics systems for nanotechnology and ecology research. MOJ Ecol Environ Sci. 2018;3(5):306‒309.
46. Afonin SM. Electromagnetoelastic actuator for large telescopes. Aeron Aero Open Access J. 2018;2(5):270–272.
47. Afonin SM. Condition absolute stability of control system with electro elastic actuator for nano bioengineering and microsurgery. Surg Case Stud Open Access J. 2019;3(3):307–309.
48. Afonin SM. Piezo actuators for nanomedicine research. MOJ Appl Bio Biomech. 2019;3(2):56–57.
49. Afonin SM. Frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics. MOJ Appl Bio Biomech. 2019;3(6):137–140.
50. Afonin SM. A structural–parametric model of a multilayer electroelastic actuator for mechatronics and nanotechnology. Chapter 7 in Advances in Nanotechnology. Eds. Bartul Z, Trenor J, Nova Science, New York. 2019;22:169–186.
51. Afonin SM. Electroelastic digital–to–analog converter actuator nano and microdisplacement for nanotechnology. Chapter 6 in Advances in Nanotechnology. Eds. Bartul Z, Trenor J, Nova Science, New York. 2020;24:205–218.
52. Afonin SM. Characteristics of an electroelastic actuator nano– and microdisplacement for nanotechnology. Chapter 8 in Advances in Nanotechnology. Eds. Bartul Z, Trenor J, Nova Science, New York. 2021;25:251–266.
53. Afonin SM. Rigidity of a multilayer piezoelectric actuator for the nano and micro range. Russ Eng Res. 2021;41(4):285–288.
54. Afonin SM. Structural scheme of electroelastic actuator for nanomechatronics, Chapter 40 in Advanced Materials. Proceedings of the International Conference on “Physics and Mechanics of New Materials and Their Applications”, PHENMA 2019. Eds: Parinov IA, Chang SH, Long BT. 2019;487–502.
55. Afonin SM. Absolute stability of control system for deformation of electromagnetoelastic actuator under random impacts in nanoresearch. Chapter 3 in Physics and Mechanics of New Materials and Their Applications. 2021;519–531.
56. Afonin SM. Electroelastic actuator of nanomechatronics systems for nanoscience. Chapter 2 in Recent Progress in Chemical Science Research. Volume 6. Ed. Min HS, B P International, India, UK. London. 2023;15–27.
57. Afonin SM. Harmonious linearization of hysteresis characteristic of an electroelastic actuator for nanomechatronics systems. Chapter 34 in Physics and Mechanics of New Materials and Their Applications. 2023;20:419–428.
58. Bhushan B. Springer Handbook of Nanotechnology. New York: Springer. 2004;1222.
59. Nalwa HS. Encyclopedia of Nanoscience and Nanotechnology. Los Angeles: Am Sci Publish. 2004.