Electromagnetoelastic actuator for large telescopes

doi:10.15406/aaoaj.2018.02.00060

eISSN: 2576-4500

Aeronautics and Aerospace Open Access Journal

Short Communication Volume 2 Issue 5

Electromagnetoelastic actuator for large telescopes

Afonin SM

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

National Research University of Electronic Technology (MIET), Russia

Correspondence: Afonin SM, National Research University of Electronic Technology (MIET), Moscow, Russia

Received: August 17, 2018 | Published: September 18, 2018

Citation: Afonin SM. Electromagnetoelastic actuator for large telescopes. Aeron Aero Open Access J. 2018;2(5):270-272. DOI: 10.15406/aaoaj.2018.02.00060

Download PDF

Abstract

The structural diagram and the transfer functions, the characteristics of the electromagnetoelastic actuator for the large telescopes and the cosmic telescopes are obtained. The generalized structural diagram, the matrix transfer functions of the electromagnetoelastic actuator are described the characteristics of the actuator with regard to its physical parameters and external load.

Keywords: electromagnetoelastic actuator, nano-and microdisplacement, electromagnetoelasticity, structural diagram, piezoactuator, transfer function

Introduction

The electromagnetoelastic actuator for the nano- and microdisplacement on the piezoelectric, piezomagnetic, electrostriction, magnetostriction effects is used in the electromechanics systems for the large telescopes and for the cosmic telescopes.¹⁻⁸ The mathematical model, the structural diagram and transfer functions of the electromagnetoelastic actuator are calculated for designing the control system for the large telescopes and the adaptive optics.⁹⁻¹⁸ The structural diagram and transfer functions the electromagnetoelastic actuator based on the electromagnetoelasticity make it possible to describe the dynamic and static properties of the electromagnetoelastic actuator for the large telescopes, the cosmic telescopes and the adaptive optics with regard to its physical parameters and external load.¹⁹⁻²²

Structural diagram

The structural diagram of the electromagnetoelastic actuator for the large telescopes, the cosmic telescopes and the adaptive optics is changed from Cady and Mason electrical equivalent circuits. The method of mathematical physics with Laplace transform is applied for the solution the wave equation and for the determination the structural diagram of the electromagnetoelastic actuator for the nano- and microdisplacement.¹⁻¹⁸

The generalized equation of the electromagnetoelasticity^8,11,14has the following form

$S_{i} = ν_{m i} Ψ_{m} (t) + s_{i j}^{Ψ} T_{j} (x, t)$ $S_{i} = ν_{m i} Ψ_{m} (t) + s_{i j}^{Ψ} T_{j} (x, t)$ (1)

where $S_{i} = \partial ξ (x, t) / \partial x$ $S_{i} = \partial ξ (x, t) / \partial x$ is the relative displacement along axis i of the cross section of the piezoactuator or the piezoplate, $Ψ_{m} = {E_{m}, D_{m}, H_{m}$ $Ψ_{m} = {E_{m}, D_{m}, H_{m}$ is the control parameter, $E_{m}$ $E_{m}$ is the electric field strength for the voltage control along axis m, $D_{m}$ $D_{m}$ is the electric induction for the current control along axis m, $H_{m}$ $H_{m}$ for magnetic field strength control along axis m, $T_{j}$ $T_{j}$ is the mechanical stress along axis j, $ν_{m i}$ $ν_{m i}$ is the electromagnetoelastic module, for example, the piezoelectric module, $s_{i j}^{Ψ}$ $s_{i j}^{Ψ}$ is the elastic compliance for the control parameter $Ψ = const$ $Ψ = const$ , and the indexes i=1, 2, … , 6; j=1, 2, … , 6; m=1, 2, 3. The main size of the electromagnetoelastic actuator is determined us the working length $l = {δ, h, b$ $l = {δ, h, b$ in form the thickness, the height and the width for the longitudinal, transverse and shift piezoeffect.

For the construction the structural diagrams of the electromagnetoelastic actuator is used the wave equation^8,10,14for the wave propagation in a long line with damping but without distortions. With using Laplace transform is obtained the linear ordinary second-order differential equation with p parameter. The original problem for the partial differential equation of hyperbolic type using the Laplace transform is reduced to the simpler problem^8,14for the linear ordinary differential equation

$\frac{d^{2} Ξ (x, p)}{d x^{2}} - γ^{2} Ξ (x, p) = 0$ $\frac{d^{2} Ξ (x, p)}{d x^{2}} - γ^{2} Ξ (x, p) = 0$ (2)

where $Ξ (x, p)$ $Ξ (x, p)$ is the Laplace transform of the displacement of section of the actuator, $γ = p / c^{Ψ} + α$ $γ = p / c^{Ψ} + α$ is the propagation coefficient, $c^{Ψ}$ $c^{Ψ}$ is the sound speed for the control parameter $Ψ = const$ $Ψ = const$ , $α$ $α$ is the damping coefficient, C and B are constants.

The mathematical model and the generalized structural diagram of the electromagnetoelastic actuator for the nano- and microdisplacement^7,14on Figure 1 are determined, using method of the mathematical physics for the solution of the wave equation, the boundary conditions and the equation of the electromagnetoelasticity, in the following form

$\begin{matrix} Ξ_{1} (p) = {[1 / (M_{1} p^{2})]} \times \times {- F_{1} (p) + {(1 / χ_{i j}^{Ψ})} [ν_{m i} Ψ_{m} (p) - {[γ / sh (l γ)]} [ch (l γ) Ξ_{1} (p) - Ξ_{2} (p)]]} \end{matrix}$ $\begin{array}{l} Ξ_{1} (p) = {[1 / (M_{1} p^{2})]}^{} \times \\ \times {- F_{1} (p) + {(1 / χ_{i j}^{Ψ})}_{}^{} [ν_{m i} Ψ_{m} (p) - {[γ / sh (l γ)]}_{} [ch (l γ) Ξ_{1} (p) - Ξ_{2} (p)]]} \end{array}$ (3)

$\begin{matrix} Ξ_{2} (p) = {[1 / (M_{2} p^{2})]} \times \times {- F_{2} (p) + {(1 / χ_{i j}^{Ψ})} [ν_{m i} Ψ_{m} (p) - {[γ / sh (l γ)]} [ch (l γ) Ξ_{2} (p) - Ξ_{1} (p)]]} \end{matrix}$ $\begin{array}{l} Ξ_{2} (p) = {[1 / (M_{2} p^{2})]}^{} \times \\ \times {- F_{2} (p) + {(1 / χ_{i j}^{Ψ})}_{}^{} [ν_{m i} Ψ_{m} (p) - {[γ / sh (l γ)]}_{} [ch (l γ) Ξ_{2} (p) - Ξ_{1} (p)]]} \end{array}$

where $v_{m i} = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} d_{33}, d_{31}, d_{15} g_{33}, g_{31}, g_{15} d_{33}, d_{31}, d_{15} \end{matrix}$ $v_{m i} = {\begin{matrix} d_{33}, d_{31}, d_{15} \\ g_{33}, g_{31}, g_{15} \\ d_{33}, d_{31}, d_{15} \end{matrix}$ , $Ψ_{m} = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} E_{3}, E_{1} D_{3}, D_{1} H_{3}, H_{1} \end{matrix}$ $Ψ_{m} = {\begin{matrix} E_{3}, E_{1} \\ D_{3}, D_{1} \\ H_{3}, H_{1} \end{matrix}$ , $s_{i j}^{Ψ} = ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \begin{matrix} s_{33}^{E}, s_{11}^{E}, s_{55}^{E} s_{33}^{D}, s_{11}^{D}, s_{55}^{D} s_{33}^{H}, s_{11}^{H}, s_{55}^{H} \end{matrix}$ $s_{i j}^{Ψ} = {\begin{matrix} s_{33}^{E}, s_{11}^{E}, s_{55}^{E} \\ s_{33}^{D}, s_{11}^{D}, s_{55}^{D} \\ s_{33}^{H}, s_{11}^{H}, s_{55}^{H} \end{matrix}$ ,

$c^{Ψ} = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} c^{E} c^{D} c^{H} \end{matrix}$ $c^{Ψ} = {\begin{matrix} c^{E} \\ c^{D} \\ c^{H} \end{matrix}$ , $γ = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} γ^{E} γ^{D} γ^{H} \end{matrix}$ $γ = {\begin{matrix} γ^{E} \\ γ^{D} \\ γ^{H} \end{matrix}$ , $l = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} δ h b \end{matrix}$ $l = {\begin{matrix} δ \\ h \\ b \end{matrix}$ , $χ_{i j}^{Ψ} = s_{i j}^{Ψ} / S_{0}$ $χ_{i j}^{Ψ} = s_{i j}^{Ψ} / S_{0}$ ,

$ν_{m i}$ $ν_{m i}$ is the electromagnetoelastic module, $Ψ_{m} = {E_{m}, D_{m}, H_{m}$ $Ψ_{m} = {E_{m}, D_{m}, H_{m}$ is the control parameter, $E_{m}$ $E_{m}$ is the electric field strength for the voltage control along axis m, $D_{m}$ $D_{m}$ is the electric induction for the current control along axis m, $H_{m}$ $H_{m}$ for magnetic field strength control along axis m, $s_{i j}^{Ψ}$ $s_{i j}^{Ψ}$ is the elastic compliance, $d_{m i}$ $d_{m i}$ is the piezomodule at the voltage-controlled piezoactuator or the magnetostrictive coefficient for the magnetostrictive actuator, $g_{m i}$ $g_{m i}$ is the piezomodule at the current-controlled piezoactuator, $S_{0}$ $S_{0}$ is the cross section area, $M_{1}$ $M_{1}$ , $M_{2}$ $M_{2}$ are the mass of the load, $Ξ_{1} (p)$ $Ξ_{1} (p)$ , $Ξ_{2} (p)$ $Ξ_{2} (p)$ and $F_{1} (p)$ $F_{1} (p)$ , $F_{2} (p)$ $F_{2} (p)$ are the Laplace transforms of the appropriate displacements and the forces on the faces 1, 2. The structural diagrams of the magnetostrictive actuator, the voltage-controlled or current-controlled piezoactuator are determined from the mathematical model of the actuator.

Matrix transfer function

The matrix transfer function of the electromagnetoelastic actuator^8,14,18for the large telescopes, the cosmic telescopes and the adaptive optics is deduced from its mathematical model (3) in the following form

$(Ξ (p)) = (W (p)) (P (p))$ $(Ξ (p)) = (W (p)) (P (p))$ (4)

$(Ξ (p)) = (\begin{matrix} Ξ_{1} (p) Ξ_{2} (p) \end{matrix})$ $(Ξ (p)) = (\begin{matrix} Ξ_{1} (p) \\ Ξ_{2} (p) \end{matrix})$ , $(W (p)) = (\begin{matrix} \begin{matrix} W_{11} (p) & W_{12} (p) & W_{13} (p) \end{matrix} \begin{matrix} W_{21} (p) & W_{22} (p) & W_{23} (p) \end{matrix} \end{matrix})$ $(W (p)) = (\begin{matrix} \begin{matrix} W_{11} (p) & W_{12} (p) & W_{13} (p) \end{matrix} \\ \begin{matrix} W_{21} (p) & W_{22} (p) & W_{23} (p) \end{matrix} \end{matrix})$

$(P (p)) = (\begin{matrix} Ψ_{m} (p) \\ F_{1} (p) \\ F_{2} (p) \end{matrix})$

where $(Ξ (p))$ is the column-matrix of the Laplace transforms of the displacements for the faces of the electromagnetoelastic actuator, $(W (p))$ is the matrix transfer function, $(P (p))$ the column-matrix of the Laplace transforms of the control parameter and the forces.

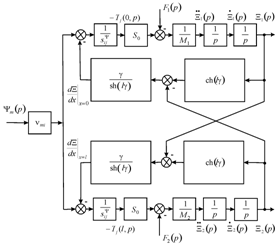
Figure 1 Generalized structural diagram of electromagnetoelastic actuator for the nano- and microdisplacement..

Conclusion

The mathematical model, the structural diagram and transfer functions of the electromagnetoelastic actuator for the large telescopes, the cosmic telescopes and the adaptive optics are obtained. The generalized structural diagram, the transfer functions of the electromagnetoelastic actuator for the nano- and microdisplacement are described the characteristics of the electromagnetoelastic actuator with regard to its physical parameters, external load.