Nanopiezoactuator for astrophysics equipment

doi:10.15406/paij.2023.07.00302

eISSN: 2576-4543

Physics & Astronomy International Journal

Mini Review Volume 7 Issue 2

Nanopiezoactuator for astrophysics equipment

Afonin SM

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

National Research University of Electronic Technology, Russia

Correspondence: Afonin Sergey Mikhailovich, National Research University of Electronic Technology, MIET, 124498, Moscow, Russia

Received: May 15, 2023 | Published: June 16, 2023

Citation: Afonin SM. Nanopiezoactuator for astrophysics equipment. Phys Astron Int J. 2023;7(2):153-155. DOI: 10.15406/paij.2023.07.00302

Download PDF

Abstract

For astrophysics equipment and composite telescope the parameters and the characteristics of the nanopiezoactuator are obtained. The functions of the nanopiezoactuator are determined. The mechanical characteristic of the nanopiezoactuator is received.

Keywords: Nanopiezoactuator, Deformation, Characteristic, Astrophysics equipment

Introduction

The nanopiezoactuator is used for astrophysics equipment and composite telescope.^1-9 The transformation of the electric to mechanical energy is clearly for nanopiezoactuator.^3-28 The nanopiezoactuator is coming for adaptive optics, interferometry, nanotechnology.^14-43

Characteristics

For electroelastic actuator the equations of the nanopiezoactuator^4-56are received.

$(D) = (d) (T) + (ε^{T}) (E)$

$(S) = (s^{E}) (T) + {(d)}^{t} (E)$

here $(T), (E), (D), (S), (d), (ε^{T}), (s^{E})$ , t are matrixes of mechanical field intensity, electric field strength, electric induction, relative deformation, electroelastic coefficient, dielectric constant, elastic compliance, and transposed index.

Relative deformation $S_{i}$ of the nanopiezoactuator^1-49is determined.

$S_{i} = d_{m i} E_{m} + s_{i j}^{E} T_{j}$

where $d_{m i}$ is the piezocoefficient.

Differential equation of the nanopiezoactuator^3-56is received.

$\begin{array}{l} \frac{d^{2} Ξ (x, s)}{d x^{2}} - γ^{2} Ξ (x, s) = 0 \\ γ = s / c^{E} + α \end{array}$

where $Ξ (x, s), s, x, γ, α, c^{E}$ are the Laplace transform of the deformation, the operator, the coordinate, the coefficients of propagation and attenuation, the speed at $E = const$ .

At $x = 0$ and $Ξ_{1} (s) = Ξ (0, s) = 0$ the decision is obtained.

$Ξ (x, s) = Ξ_{2} (s) sh (x γ) / sh (h γ)$

At elastic-inertial load at $x = h$ and $Ξ_{2} (s) = Ξ (h, s)$ the displacement of the nanopiezoactuator is calculated.

$\frac{d Ξ_{2} (s)}{d x} = d_{31} E_{3} (s) - \frac{s_{11}^{E} M s^{2} Ξ_{2} (s)}{S_{0}} - \frac{s_{11}^{E} C_{e} Ξ_{2} (s)}{S_{0}}$

hence equation of the nanopiezoactuator has the form.

$\frac{Ξ_{2} (s) γ}{th (h γ)} + \frac{Ξ_{2} (s) s_{11}^{E} M s^{2}}{S_{0}} + \frac{Ξ_{2} (s) s_{11}^{E} C_{l}}{S_{0}} = d_{31} E_{3} (s)$

The function of the nanopiezoactuator by E is written in the form.

$W_{E} (s) = \frac{Ξ_{2} (s)}{E_{3} (s)} = \frac{d_{31} h}{M s^{2} / C_{11}^{E} + h γ cth (h γ) + C_{l} / C_{11}^{E}}$

where $Ξ_{2} (s), Ξ_{3} (s), C_{l}, C {}_{11}^{E}$ are the transforms of displacement and electric field intensity, the stiffness of load and nanopiezoactuator. The function of the nanopiezoactuator by U is received in the form.

$W_{U} (s) = \frac{Ξ_{2} (s)}{U (s)} = \frac{d_{31} h / δ}{M s^{2} / C_{11}^{E} + h γ cth (h γ) + C_{l} / C_{11}^{E}}$

For the nanopiezoactuator its reverse and direct coefficients are calculated.

$k_{r} = k_{d} = \frac{d_{m i} S_{0}}{δ s_{i j}}$

For elastic-inertial load at mass of load with the load mass much greater than the mass of actuator $M_{2} > > m$ the scheme of the nanopiezoactuator with one fixed face on Figure 1 is calculated.

The expression by U of the nanopiezoactuator for Figure 1 is calculated.

Figure 1 Scheme of nanopiezoactuator.

$\begin{array}{l} W (s) = Ξ_{2} (s) / U (s) = k_{r} / N (s) \\ N (s) = a_{0} s^{3} + a_{1} s^{2} + a_{2} s + a_{3} \\ a_{0} = R C_{0} M_{2}, a_{1} = M_{2} + R C_{0} k_{v} \\ a_{2} = k_{v} + R C_{0} C {}_{i j}+ R C_{0} C {}_{e}+ R k_{r} k_{d}, a_{3} = C {}_{e}+ C {}_{i j} \end{array}$

here $k_{v}$ - the coefficient of damping.

For the transverse nanopiezoactuator for $R = 0$ the expression by U is determined.

$\begin{array}{l} W (s) = \frac{Ξ_{2} (s)}{U (s)} = \frac{k_{31}^{U}}{T_{t}^{2} s^{2} + 2 T_{t} ξ_{t} s + 1} \\ k_{31}^{U} = d_{31} (h / δ) / (1 + C_{l} / C_{11}^{E}) \\ T_{t} = \sqrt{M / (C_{l} + C_{11}^{E})}, ω_{t} = 1 / T_{t} \end{array}$

At M = 1 kg, $C_{l}$ = 0.2×10⁷ N/m, $C_{11}^{E}$ = 2×10⁷ N/m the parameters of the transverse nanopiezoactuator are evaluated $T_{t}$ = 0.21×10^-3 s, $ω_{t}$ = 4.7×10³ s^-1 at error 10%.

Mechanical characteristic of the nanopiezoactuator is determined.

$\begin{array}{l} Δ l = Δ l_{max} (1 - F / F_{max}) \\ Δ l_{max} = d_{m i} l E_{m} \\ F_{max} = d_{m i} S_{0} E_{m} / s_{i j}^{E} \end{array}$

where the maximums $Δ l_{max}$ and $F_{max}$ of the displacement and the force of the nanopiezoactuator are determined.

The relative longitudinal deformation^8-18is determined.

$S_{3} = d_{33} E_{3} + s_{33}^{E} T_{3}$

where $d_{33}$ is the longitudinal piezocoefficient.

The mechanical characteristic of the longitudinal nanopiezoactuator has the form.

$\begin{array}{l} Δ δ = Δ δ_{max} (1 - F / F_{max}) \\ Δ δ_{max} = d_{33} δ E_{3} = d_{33} U \\ F_{max} = d_{33} S_{0} E_{3} / s_{33}^{E} \end{array}$

At $E_{3}$ = 0.6∙10⁵ V/m, $S_{0}$ = 1.5∙10^-4 m², $δ$ = 2.5∙10^-3 m, $d_{33}$ = 4∙10^-10 m/V, $s_{33}^{E}$ = 15∙10^-12 m²/N for the longitudinal nanopiezoactuator from PZT its parameters received $Δ δ_{max}$ = 60 nm, $F_{max}$ = 240 N on Figure 2 with error 10%.

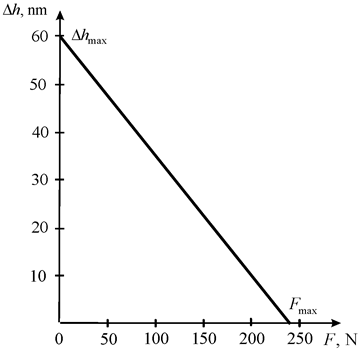
Figure 2 Mechanical characteristic.

The maximums of the displacement $Δ h_{max}$ and force $F_{max}$ for the transverse nanopiezoactuator are received in the form.

$\begin{array}{l} Δ h_{max} = d_{31} h E_{3} = d_{31} (h / δ) U \\ F_{max} = d_{31} S_{0} E_{3} / s_{11}^{E} \end{array}$

where $d_{31}$ is the transverse piezocoefficient.

The static transverse displacement at elastic load is determined.

$Δ h = \frac{d_{31} (h / δ) U}{1 + C_{l} / C_{11}^{E}} = k_{31}^{U} U$

At $d_{31}$ = 2∙10^-10 m/V, $h / δ$ = 21, $C_{l} / C_{11}^{E}$ = 0.1 the parameter $k_{31}^{U}$ = 3.8 nm/V is evaluated at error 10%.

Conclusion

The deformation of the nanopiezoactuator is determined for astrophysics. The characteristics of the nanopiezoactuator are evaluated for composite telescope. The characteristics for the nanopiezoactuator are calculated.