The DAC electro elastic engine is used for nanomedicine and nanotechnology. The mechanical and regulation characteristics of the DAC electro elastic engine are found. In work we are consider the characteristics of the DAC transverse, longitudinal and shift piezo engines. The characteristics of the DAC electro elastic engine are determined by using method of mathematical physics.

Keywords: DAC electro elastic engine, DAC piezo engine, characteristics, nanomedicine

The digital-to-analog converter (DAC) electro elastic engine on piezoelectric or electrostriction effect is used for nanomedicine and nanotechnology,¹⁻¹⁰ adaptive optics, interferometers, nanomanipulators, nanopumps, microsurgery, scanning microscopy and nanophysics.⁸⁻²⁹

The problem of use the coded control and the DAC electro elastic engine is promising for nanomedicine. The DAC electro elastic engine can be applied to increase the range of displacement from nano- to microdisplacement in control systems.¹⁻¹⁰

The DAC electro elastic engine consists of N sections with n electro elastic layers. The electro elastic layers in the DAC electro elastic engine are connected electrically in parallel and mechanically in series for the section. In this work, the mechanical and regulation characteristics of the DAC electro elastic engine are determined by using method of mathematical physics.

DAC electro elastic engine

The number of the layers in the section of the DAC electro elastic engine is equal to the degree of 2. For the DAC transverse piezo engine for nanomedicine on Figure 1 its equation of the reverse piezo effect¹⁻¹² has the form.

$S_{\text{1}}=d_{\text{31}}{E}_{\text{3}}+s_{\text{11}}^E{T}_{\text{1}}$

here S₁, E₃, T₁, d₃₁, $s_{\text{11}}^E$  − the relative deformation on axis 1, the electric field stress on axis 3, the mechanical stress on axis 1, the transverse piezo module and the elastic compliance at $E=\text{const}\text{.}$

We have the displacement $\Delta l_k$  of the section k with the length $l_k$  of the DAC transverse piezo engine at $F=\text{0}$  in the form

$\Delta l_k={\text{2}}^{k-\text{1}}\frac{d_{\text{31}}{l}_{\text{1}}U}{\delta }={\text{2}}^{k-\text{1}}\Delta l_{\text{1}}=\frac{d_{\text{31}}{l}_{k}U}{\delta }$

here $\text{1}\le k\le N$ , $\delta$  − is the thickness of the DAC electro elastic engine.

Therefore, the displacement of the DAC transverse piezo engine on Figure 1 at $F=\text{0}$  is found in the form

$\Delta l=\frac{d_{\text{31}}{l}_{\text{1}}U}{\delta }\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)=\Delta l_{\text{1}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)$

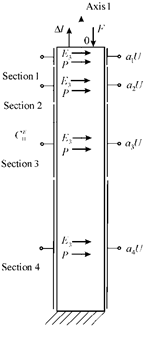
Figure 1 DAC transverse piezo engine.

here l, $a_k$  − the length of the DAC transverse piezo engine and the binary code of the section.

The displacement of the DAC transverse piezo engine has the form

$\Delta l=\frac{d_{\text{31}}{l}_{\text{1}}U}{\delta }\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)-\frac{s_{\text{11}}^{E}lF}{S_{\text{0}}}$

Therefore, the displacement is written in the form

$\Delta l=\frac{d_{\text{31}}{l}_{\text{1}}U}{\delta }\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)-\frac{F}{C{}_{\text{11}}{}^E}$

here $C{}_{\text{11}}{}^E=S_{\text{0}}/\left(s_{\text{11}}^{E}l\right)$  − the rigidity of the DAC transverse piezo engine. In this equation we have the maximum displacement and maximum force of the DAC transverse piezo engine in the form

$\Delta l_{\max }=\frac{d_{\text{31}i}{l}_{\text{1}}U}{\delta }\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)=\Delta l_{\text{1}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)$  at $F=\text{0}$

$F_{\max }=\frac{d_{\text{31}}{l}_{\text{1}}U}{\delta }\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)C{}_{\text{11}}{}^E$  at $\Delta l=\text{0}$

In general for the digital-to-analog converter (DAC) electro elastic engine its equation of the reverse piezo effect¹⁻¹⁹ has the form:

$S_i=d_{mi}{E}_m+s_{ij}^E{T}_j$

here $S_i$ , $E_m$ , $T_j$ , $d_{mi}$  and $s_{ij}^E$  − the relative deformation on axis i, the electric field stress on axis m, the mechanical stress on axis j, the piezo module and the elastic compliance at $E=\text{const}$ .

Characteristics DAC electro elastic engine

In general the mechanical characteristic of the DAC electro elastic engine is written in the form

$\Delta l=\Delta l_{\max }\left(\text{1}-F/F_{\max }\right)$

here $\Delta l_{\max }$ and $F_{\max }$  are written in the form

$\Delta l_{\max }=\frac{d_{mi}{l}_{\text{1}}U}{\delta }\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)=\Delta l_{\text{1}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)$  at $F=\text{0}$

$F_{\max }=\frac{d_{mi}{l}_{\text{1}}U}{\delta }\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)C{}_{ij}{}^E$  at $\Delta l=\text{0}$

$C{}_{ij}{}^E=S_{\text{0}}/\left(s_{ij}^{E}l\right)$ , $\Delta l_{\text{1}}=d_{mi}{l}_{\text{1}}U/\delta$ , $l={\displaystyle \sum _{k=\text{1}}^N{l}_k=}\left({\text{2}}^N-\text{1}\right)l_{\text{1}}$

here $C{}_{ij}{}^E$ , $\Delta l_{\text{1}}$ , l − the rigidity of the DAC electro elastic engine, the displacement of first section, the length of the DAC electro elastic engine.

The static characteristics of the DAC electro elastic engine at elastic load has the form

$\Delta l=\frac{d_{mi}{l}_{\text{1}}U}{\delta }\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)-\frac{C_e\Delta l}{C{}_{ij}{}^E}$

In general the adjustment characteristic of the DAC electro elastic engine on Figure 2 is found in the form

$\Delta l=k_{a}U=\frac{\left(d_{mi}{l}_{\text{1}}/\delta \right)U}{\left(\text{1}+C_e/C{}_{ij}{}^E\right)}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)=\Delta l_{\text{1}}с$ ,

$k_a=\frac{\left(d_{mi}{l}_{\text{1}}/\delta \right)}{\left(\text{1}+C_e/C{}_{ij}{}^E\right)}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)$ ,

$\Delta l_{\text{1}}=\frac{\left(d_{mi}{l}_{\text{1}}/\delta \right)U}{\text{1}+C_e/C{}_{ij}{}^E}$

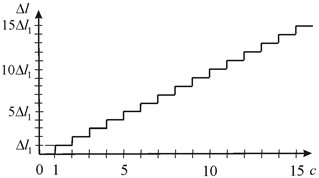
Figure 2 Adjustment characteristic of DAC electro elastic engine.

here $с={\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}$  − the decimal code.

Therefore, for the DAC piezo engine from PZT ceramic at $d_{\text{31}}$  = 0.2 nm/V, $d_{\text{33}}$  = 0.4 nm/V and $d_{\text{15}}$  = 0.5 nm/V, $l_{\text{1}}/\delta$  = 1, $C_e$  = 0, and U =20 V we have on Figure 2, therefore, the parameters for the DAC transverse, longitudinal and shift piezo engines $\Delta l_{\text{1}}$  = 4 nm, $\Delta l_{\text{1}}$  = 8 nm and $\Delta l_{\text{1}}$  = 10 nm with error 10%.

Let us consider the mechanical characteristic of the DAC longitudinal piezo engine.

Its maximum parameters of the mechanical characteristic of the DAC longitudinal piezo engine on Figure 3 are determined in the form

$\Delta l_{\max }=d_{\text{33}}U\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)=\Delta l_{\text{1}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)$
$F_{\max }=d_{\text{33}}U\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)C{}_{\text{33}}{}^E$

here $C{}_{\text{33}}{}^E=S_{\text{0}}/\left(s_{\text{33}}^{E}l\right)$  is the rigidity of the rigidity of the DAC longitudinal piezo engine.

For the DAC longitudinal piezo engine from PZT ceramic at $d_{\text{33}}$  = 0.4 nm/V, $l_{\text{1}}/\delta$  = 1, $C{}_{\text{33}}{}^E$  = 4×10⁸ N/m, and U = 60 V for 1) $a_{\text{1}}$  = 1, $a_{\text{2}}$  = 0, $a_{\text{3}}$  = 0, $a_{\text{4}}$  = 0; 2) $a_{\text{1}}$  = 1, $a_{\text{2}}$  = 1,$a_{\text{3}}$ = 0, $a_{\text{4}}$ = 0; 3) $a_{\text{1}}$ = 1, $a_{\text{2}}$ = 1, $a_{\text{3}}$ =1, $a_{\text{4}}$ = 0; 4) $a_{\text{1}}$ = 1, $a_{\text{2}}$= 1, $a_{\text{3}}$=1, $a_{\text{4}}$= 1 the parameters of the DAC longitudinal piezo engine on Figure 3 are determined in the form 1) $\Delta l_{\max }$  = 24 nm, $F_{\max }$  = 9.6 N; 2) $\Delta l_{\max }$  = 72 nm, $F_{\max }$  = 28.8 N; 3) $\Delta l_{\max }$  = 168 nm, $F_{\max }$  = 67.2 N; 4) $\Delta l_{\max }$  = 360 nm, $F_{\max }$  = 144 N with error 10%.

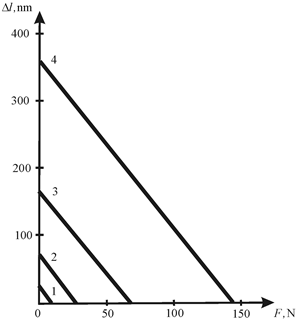
Figure 3 Mechanical characteristic of DAC longitudinal piezo engine.

Thus, the mechanical and regulation characteristics of the DAC electro elastic engine are found.

Through the use of mathematical physics we have obtained the mechanical and regulation characteristics of the DAC electro elastic engine for nanomedicine. The problem of use the coded control and the DAC electro elastic engine are promising for nanomedicine and nanotechnology. The generalized mechanical and adjustment characteristics of DAC electro elastic engine are determined using the equations of the reverse piezo effect and the mechanical load. Additionally, we have obtained the mechanical and adjustment characteristics of the DAC transverse, longitudinal and shift piezo engines.

The DAC electro elastic engine is used for nanomedicine in Nano pumps, Nano manipulators, scanning microscopy, and adaptive optics. The characteristics of the DAC electro elastic engine are obtained by using method of mathematical physics. The parameters and the characteristics of the DAC transverse, longitudinal and shift piezo engines are determined.

In general the mechanical and regulation characteristics of the DAC electro elastic engine are found for nanomedicine and nanotechnology.

None.

None.

The author declares that there is no conflict of interest.

1. Uchino K. Piezoelectric actuator and ultrasonic motors. Boston, MA: Kluwer Academic Publisher. 1997;350.
2. Schultz J, Ueda J, Asada H. Cellular Actuators. Butterworth–Heinemann Publisher, Oxford. 2017;382.
3. Afonin SM. Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Doklady Math. 2006;74(3):943–948.
4. Bhushan B. Springer handbook of nanotechnology. New York: Springer. 2004;1222.
5. Shevtsov SN, Soloviev AN, Parinov IA, et al. Piezoelectric actuators and generators for energy harvesting. Res Develop. 2018;2018:182.
6. Afonin SM. Generalized parametric structural model of a compound elecromagnetoelastic transduser. Doklady Physics. 2005;50(2): 77–82.
7. Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transducer. Doklady Physics. 2008;53(3):137–143.
8. Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady Math. 2006;73(2): 307–313.
9. Afonin SM. Optimal control of a multilayer electroelastic engine with a longitudinal piezoeffect for nanomechatronics systems. Appl Sys Innovat. 2020;3(4):1–7.
10. Afonin SM. Coded сontrol of a sectional electroelastic engine for nanomechatronics systems. Appl Sys Innovat. 2021;4(3):1–11.
11. Cady WG. Piezoelectricity: an introduction to the theory and applications of electromechancial phenomena in crystals. McGraw–Hill Book Company, New York, London. 1946;806.
12. Mason W. Physical acoustics: principles and methods. Vol. 1. Part A. methods and devices. Academic Press, New York, 1964;515.
13. Liu Y, Zeng A, Zhang S, et al. An experimental investigation on polarization process of a PZT–52 tube actuator with interdigitated electrodes. Micromachines. 2022;13(10):1760.
14.  Jang SM, Yang SC. Highly piezoelectric BaTiO3 nanorod bundle arrays using epitaxially grown TiO2 nanomaterials. Nanotechnology. 2018;29(23):235602.
15. Afonin SM. Structural–parametric model and transfer functions of electroelastic actuator for nano and microdisplacement. Chapter 9 in piezoelectrics and nanomaterials: fundamentals, developments and applications. Ed. Parinov IA. Nova Science, New York. 2015;225–242.
16. Afonin SM. Structural–parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. Int J Phys. 2017;5(1):9–15.
17. Afonin SM. Structural–parametric model multilayer electromagnetoelastic actuator for nanomechatronics. Int J Phys. 2019;7(2):50–57.
18. Afonin SM. Structural–parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 2018;7(1):1–9.
19. Afonin SM. Structural–parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 2019;8(3):1–14.
20. Afonin SM. Condition absolute stability control system of electromagnetoelastic actuator for communication equipment. Transac Network Commun. 2020;8(1):8–15.
21. Afonin SM. Rigidity of a multilayer piezoelectric actuator for the nano and micro range. Russia Eng Res. 2021;41(4): 285–288.
22. Afonin SM. Structural scheme of an electromagnetoelastic actuator for nanotechnology research. Chapter 45. Phys Mech New Mat Appl. 2024;486–501.
23. Afonin SM. Piezoengine for nanomedicine and applied bionics. MOJ Appl Bio Biomech. 2022;6(1):30–33.
24. Afonin SM. Characteristics of an electroelastic actuator nano– and microdisplacement for nanotechnology. Chapter 8 in Advances in Nanotechnology. Eds. Bartul Z, Trenor J, Nova Science, New York. 2021;25:251–266.
25. Afonin SM. Absolute stability of system with nano piezoengine for biomechanics. MOJ Appl Bio Biomech. 2023;7(1):211–213.
26. Afonin SM. Electroelastic actuator of nanomechatronics systems for nanoscience. Chap 2 in recent progress in chemical science research. Ed. Min HS, B P International, India, UK. London, 2023;6:15–27.
27.  Afonin SM. Harmonious linearization of hysteresis characteristic of an electroelastic actuator for nanomechatronics systems. Chap 34 in Physics and mechanics of new materials and their applications. 2023;419–428.
28. Afonin SM. Structural parametric model and diagram of electromagnetoelastic actuator for nanodisplacement in chemistry and biochemistry research. Chap 7 in Curr Topic Chem Biochem. 2023;9:77–95.
29. Nalwa HS. Encyclopedia of nanoscience and nanotechnology. Los Angeles: American Scientific Publishers. 2004;10.