The structural scheme of an electromagnetoelastic actuator for nano biomechanics is found. The structural scheme of an electromagnetoelastic actuator has difference in the visibility of energy conversion from Cady and Mason electrical equivalent circuits of a piezo vibrator. The electromagnetoelasticity equation and the differential equation of the actuator are solved to construct the structural scheme of the actuator. The structural scheme of the piezo actuator is obtained by using the reverse and direct piezoelectric effects. The transfer functions of an electromagnetoelastic actuator are written.

Keywords: structural scheme, electromagnetoelastic actuator, Characteristic, Piezo actuator, Nano biomechanics, Deformation, Transfer function

Electromagnetoelastic actuator in the form of piezo actuator or magnetostriction actuator is used in nanomanipulators, laser systems, nanopumps, scanning microscopy for nano biomechanics. The piezo actuator is widely applied for nano biomechanics in medical equipment for precise instrument, in optical-mechanical devices and adaptive optics systems.^1-14

The electromagnetoelasticity equation and the differential equation of the actuator are solved to found the structural scheme of the actuator. The structural scheme of an electromagnetoelastic actuator for nano biomechanics has difference in the visibility of energy conversion from Cady and Mason electrical equivalent circuits of a piezo vibrator. The structural scheme of electromagnet elastic actuator is obtained by applying of electromagnetoelasticity, mathematical physics and transform of Laplace.^4-11

The structural scheme of an electromagnetoelastic actuator for nano biomechanics is changed from Cady and Mason electrical equivalent circuits.^5-8 The equation of electromagnetoelasticity^3-15 has the form

$S_i=d_{mi}{\Psi }_m+s_{ij}^{\Psi }{T}_j$

where $S_i$ , $d_{mi}$ , ${\Psi }_m$ , $s_{ij}^{\Psi }$  and $T_j$  are the relative deformation, the module, the control parameter or the intensity of field, the elastic compliance, and the mechanical intensity, respectively; $i=1,2,\mathrm{...},6$ ; $m=1,2,3$ ; and $j=1,2,\mathrm{...},6$  are indexes.

The differential equation of the actuator has the form^4-38

$d^2\Xi \left(x,p\right)/d{x}^2-{\gamma }^2\Xi \left(x,p\right)=0$

$\gamma =p/c^{\Psi }+\alpha$

Where $\Xi \left(x,p\right)$  is the transform of Laplace for displacement; $p$ , $\gamma$ , $c^{\Psi }$ , $\alpha$  are the operator of transform, the coefficient of wave propagation, the speed of sound, the coefficient of attenuation.

The system of the equations the transform of Laplace for the forces on the faces actuator is found^10-42

$M_1{p}^2{\Xi }_1\left(p\right)+F_1\left(p\right)=S_0{T}_j\left(0,p\right)$

$-M_2{p}^2{\Xi }_2\left(p\right)-F_2\left(p\right)=S_0{T}_j\left(l,p\right)$

where $M_1$ , $M_2$ , ${\Xi }_1\left(p\right)$ , ${\Xi }_2\left(p\right)$ , $F_1\left(p\right)$ , $F_2\left(p\right)$ , $S_0$ are the masses on two end faces, the transforms of Laplace for displacements  and the forces on two end faces,  the area of actuator.

The system of the equations the transform of Laplace for stresses acting on the faces actuator has the form

$T_j\left(0,p\right)=\frac{1}{s_{ij}^{\Psi }}{\frac{d\Xi \left(x,p\right)}{dx}|}_{x=0}-\frac{d_{mi}}{s_{ij}^{\Psi }}{\Psi }_m\left(p\right)$

$T_j\left(0,p\right)=\frac{1}{s_{ij}^{\Psi }}{\frac{d\Xi \left(x,p\right)}{dx}|}_{x=0}-\frac{d_{mi}}{s_{ij}^{\Psi }}{\Psi }_m\left(p\right)$

The system of equations for the structural scheme of an electromagnetoelastic actuator for nano biomechanics on Figure 1 has the form

${\Xi }_1\left(p\right)={\left(M_1{p}^2\right)}^{-1}\times \left\{\begin{array}{l}-F_1\left(p\right)+\left(1/{\chi }_{ij}^{\Psi }\right)\\ \times \left[\begin{array}{l}{d}_{mi}{\Psi }_m\left(p\right)+\left[\gamma /\text{sh}\left(l\gamma \right)\right]\\ \times \left[{\Xi }_2\left(p\right)-\text{ch}\left(l\gamma \right){\Xi }_1\left(p\right)\right]\end{array}\right]\end{array}\right\}$

${\Xi }_2\left(p\right)={\left(M_2{p}^2\right)}^{-1}\times \left\{\begin{array}{l}-F_2\left(p\right)+\left(1/{\chi }_{ij}^{\Psi }\right)\times \\ \times \left[\begin{array}{l}{d}_{mi}{\Psi }_m\left(p\right)+\left[\gamma /\text{sh}\left(l\gamma \right)\right]\\ \times \left[{\Xi }_1\left(p\right)-\text{ch}\left(l\gamma \right){\Xi }_2\left(p\right)\right]\end{array}\right]\end{array}\right\}$

Figure 1 Structural scheme of electromagnetoelastic actuator for nano biomechanics.

where ${\chi }_{ij}^{\Psi }=s_{ij}^{\Psi }/S_0$ , $d_{mi}=\{\begin{array}{c}{d}_{33},d_{31},d_{15}\\ d_{33},d_{31},d_{15}\end{array}$ , ${\Psi }_m=\{\begin{array}{c}{E}_3,E_1\\ H_3,H_1\end{array}$ , $s_{ij}^{\Psi }=\{\begin{array}{c}{s}_{33}^E,s_{11}^E,s_{55}^E\\ s_{33}^H,s_{11}^H,s_{55}^H\end{array}$ , $\gamma =\{\begin{array}{c}{\gamma }^E\\ {\gamma }^H\end{array}$ , $E$ , $H$  are the intensity of electric field  and the intensity of magnetic field.

Figure 1: Structural scheme of electromagnetoelastic actuator for nano biomechanics.

Therefore, the matrix equation of an electromagnetoelastic actuator has the form

$\left(\begin{array}{c}{\Xi }_1\left(p\right)\\ {\Xi }_2\left(p\right)\end{array}\right)=\left(\begin{array}{c}\begin{array}{ccc}{W}_{11}\left(p\right)& W_{12}\left(p\right)& W_{13}\left(p\right)\end{array}\\ \begin{array}{ccc}{W}_{21}\left(p\right)& W_{22}\left(p\right)& W_{23}\left(p\right)\end{array}\end{array}\right)\left(\begin{array}{c}{\Psi }_m\left(p\right)\\ F_1\left(p\right)\\ F_2\left(p\right)\end{array}\right)$

The equation of the direct piezoelectric effect for the piezo actuator [10-14] has the form

$D_m=d_{mi}{T}_i+{\epsilon }_{mk}^E{E}_k$

Where $D_m$ , ${\epsilon }_{mk}^E$  are the electric induction and the permittivity; $k=1,2,3$ , The coefficient of the direct piezoelectric effect $k_d$  for the Piezo actuator for $E=\text{const}$  has the form

$k_d=\frac{I_{{\dot{\Xi }}_n}\left(p\right)}{{\stackrel{•}{\Xi }}_{{}_n}\left(p\right)}=\frac{d_{mi}{S}_0}{\delta s_{ij}^E}$ , $n=1,2$

where $I_{{\dot{\Xi }}_n}\left(p\right)$ , ${\stackrel{•}{\Xi }}_{{}_n}\left(p\right)$  are transforms of Laplace for the current and the velocity; $n$  is the number of the face actuator.

The transform of Laplace for the voltage of the negative feedback has the form

$U_{{\dot{\Xi }}_n}\left(p\right)=\frac{d_{mi}{S}_{0}R}{\delta s_{ij}^E}{\stackrel{•}{\Xi }}_{{}_n}\left(p\right)$ , $n=1,2$

After conversion with negative feedbacks Figure 1 structural scheme of the piezo actuator has form Figure 2.

Figure 2 Structural scheme of piezo actuator for nano biomechanics.

The coefficient of the reverse piezoelectric effect $k_r$  has the form

$k_r=k_d=\frac{d_{mi}{S}_0}{\delta s_{ij}^E}$

Figure 2: Structural scheme of piezo actuator for nano biomechanics.

The structural scheme of the piezo actuator with one fixed end face at the lumped parameters is obtained on Figure 3.

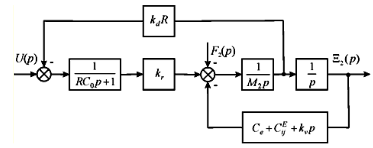
Figure 3 Structural scheme of piezo actuator with one fixed end face at elastic-inertial load.

The transfer function of the piezo actuator with one fixed end face at the lumped parameters on Figure 3 at $R=0$  has the form

$W\left(p\right)=\frac{{\Xi }_2\left(p\right)}{U\left(p\right)}=\frac{k_r}{M_2{p}^2+k_{v}p+C_{ij}^E+C{}_e}$

where $U\left(p\right)$ is a transformation of the voltage for the Piezoactuator.

Therefore, the transfer function of the piezo actuator with one fixed end face has the form

$W\left(p\right)=\frac{{\Xi }_2\left(p\right)}{U\left(p\right)}=\frac{d_{mi}\left(l/\delta \right)}{{\left(1+C_e/C_{ij}^E\right)}_{}^{}\left(T_t^2{p}^2+2T_t{\xi }_{t}p+1\right)}$

$T_t=\sqrt{M_2/\left(C_{ij}^E+C{}_e\right)}$ , ${\xi }_t=k_v/\left(2\left(C_{ij}^E+C{}_e\right)\sqrt{M_2\left(C_{ij}^E+C{}_e\right)}\right)$

$C_{ij}^E=S_0/\left(s_{ij}^{E}l\text{}\right)=1/\left({\chi }_{ij}^{E}l\right)$

where $T_t$ , ${\xi }_t$ , $C_{ij}^E$  are the time constant, the coefficient of attenuation and the stiffness of the piezo actuator at $E=\text{const}$ .

The transfer function of the piezo actuator with one fixed end face at the transverse piezoelectric effect has the form

$W\left(p\right)=\frac{{\Xi }_2\left(p\right)}{U\left(p\right)}=\frac{d_{31}h/\delta }{{\left(1+C_e/C_{11}^E\right)}_{}^{}\left(T_t^2{p}^2+2T_t{\xi }_{t}p+1\right)}$

$T_t=\sqrt{M_2/\left(C{}_e+C_{11}^E\right)}$ , ${\xi }_t=\alpha h^2{C}_{11}^E/\left(3c^E\sqrt{M\left(C_e+C_{11}^E\right)}\right)$

$C_{11}^E=S_0/\left(s_{11}^{E}h\text{}\right)=1/\left({\chi }_{11}^{E}h\right)$

where $h$ , $\delta$  are the height and the thickness of the piezo actuator.

The transient characteristic of the piezo actuator with one fixed end face at the transverse piezoelectric effect and its step input voltage has the form

${\xi }_2\left(t\right)=\frac{d_{31}\left(h/\delta \right)U}{\left(1+C_e/C_{11}^E\right)}\left(1-\frac{e^{-\frac{{\xi }_{t}t}{T_t}}}{\sqrt{1-{\xi }_t^2}}\text{sin}\left({\omega }_{t}t+{\varphi }_t\right)\right)$

${\omega }_t=\frac{\sqrt{1-{\xi }_t^2}}{T_t}$ , ${\varphi }_t=\text{arctg}\left(\frac{\sqrt{1-{\xi }_t^2}}{{\xi }_t}\right)$

At $d_{31}$  = 2∙10^-10 m/V, $h/\delta$  =16, $M_2$  = 1 kg, $C_{11}^E$  = 2.8∙10⁷ N/m, $C_e$  = 0.4∙10⁷ N/m, $U$  = 25 V parameters are obtained $T_t$  = 0.18∙10^-3 s, $\Delta h$  = 70 nm.

From the equation of electromagnetoelasticity the mechanical characteristic [10-38] of an electromagnetoelastic actuator for nano biomechanics $S_i{\left(T_j\right)}_{}^{}$  has the form

${S_i|}_{\Psi =\text{const}}={d_{mi}{\Psi }_m|}_{\Psi =\text{const}}+s_{ij}^{\Psi }{T}_j$

And the regulation characteristic [12-26] of an electromagnet elastic actuator $S_i\left({\Psi }_m\right)$  has the form

${S_i|}_{T=\text{const}}=d_{mi}{\Psi }_m+{s_{ij}^{\Psi }{T}_j|}_{T=\text{const}}$

The mechanical characteristic of an electromagnetoelastic actuator with one fixed end face for nano biomechanics has the form

$\Delta l=\Delta l_{\text{max}}\left(1-F/F_{\text{max}}\right)$

$\Delta l_{\text{max}}=d_{mi}{\Psi }_{m}l$

$F_{\text{max}}=T_{j\text{ max}}{S}_0=d_{mi}{\Psi }_m{S}_0/s_{ij}^{\Psi }$

where $\Delta l_{\text{max}}$ is the maximum of the displacement and $F_{\text{max}}$ is the maximum of the force.

Therefore, for the mechanical characteristic of the piezo actuator with one fixed end face at the transverse piezoelectric effect its parameters have the form

$\Delta h_{\text{max}}=d_{31}{E}_{3}h$

$F_{\text{max}}=d_{31}{E}_3{S}_0/s_{11}^E$

Therefore, at $d_{31}$  = 2∙10^-10 m/V, $E_3$  = 0.5∙10⁵ V/m, $h$  = 2.5∙10^-2 m, $S_0$  = 1.5∙10^-5 m², $s_{11}^E$  = 15∙10^-12 m²/N the parameters are found $\Delta h_{\text{max}}$  = 250 nm and $F_{\text{max}}$  = 10 N. Theoretical and practical parameters are coincidences with an error of 10%.

The equation of the displacement of an electromagnetoelastic actuator with one fixed end face at elastic load has the form

$\frac{\Delta l}{l}=d_{mi}{\Psi }_m-\frac{s_{ij}^{\Psi }{C}_e}{S_0}\Delta l$

$F=C_e\Delta l$

The adjustment characteristic of an electromagnetoelastic actuator with one fixed end face at elastic load has the form

$\Delta l=\frac{d_{mi}l{\Psi }_m}{1+C_e/C_{ij}^{\Psi }}$

The adjustment characteristic of the piezo actuator with one fixed end face at the transverse piezoelectric effect has the form

$\Delta h=\frac{\left(d_{31}h/\delta \right)U}{1+C_e/C_{11}^E}=k_{31}^{U}U$

$k_{31}^U=\left(d_{31}h/\delta \right)/\left(1+C_e/C_{11}^E\right)$

where $k_{31}^U$  is the transfer coefficient Therefore, at $d_{31}$  = 2∙10^-10 m/V, $h/\delta$  = 16, $C_{11}^E$  = 2.8∙10⁷ N/m, $C_e$  = 0.4∙10⁷ N/m, $U$  = 20 V parameters are found $k_{31}^U$  = 2.8 nm/V, $\Delta h$  = 56 nm.

The structural scheme of an electromagnetoelastic actuator for nano biomechanics is found. The structural scheme of an electromagnetoelastic actuator has difference in the visibility of energy conversion from the circuits of a piezo vibrator. The structural scheme of an electromagnetoelastic actuator nano biomechanics is changed from Cady and Mason electrical equivalent circuits of a piezo vibrator.

The structural scheme of an electromagnetoelastic actuator is received from the electromagnetoelasticity equation and the differential equation of actuator. The structural scheme of a piezo actuator is obtained using the equations of the reverse and direct piezoelectric effects. The back electromotive force of a piezo actuator is written from the direct piezoelectric effect. The characteristics of an electromagnetoelastic actuator for nano biomechanics are obtained. The adjustment characteristic of a piezo actuator is found.

1. Schultz J, Ueda J, Asada H. Cellular Actuators. Butterworth-Heinemann Publisher.Oxford.2017; 382 p.
2. Afonin SM. Absolute stability conditions for a system controlling the deformation of an electro magneto elastic transducer. Doklady Mathematics. 2006; 74(3): 943‒948.
3. Uchino K.Piezoelectric actuator and ultrasonic motors. Boston, MA: Kluwer Academic Publisher. 1997; 350 p.
4. Afonin SM. Generalized parametric structural model of a compound electro magneto elastic transducer. Doklady Physics. 2005;50(2): 77‒82.
5. Afonin SM.Structural parametric model of a piezoelectric nano displacement transducer. Doklady Physics.2008;53(3):137‒143.
6. Afonin SM.Solution of the wave equation for the control of an electro magneto elastic transducer. Doklady Mathematics. 2006;73(2): 307‒313.
7. Cady, W.G. Piezoelectricity: An introduction to the theory and applications of electromechanical phenomena in crystals. McGraw-Hill Book Company, New York, London,1946; 806 p.
8. Physical Acoustics: Principles and Methods. Vol.1, Part A. Methods and Devices. Ed.: Mason W. Academic Press, New York. 1964; 515 p.
9. Zwillinger D. Handbook of Differential Equations. Academic Press, Boston. 1989; 673 p.
10. Afonin SM. A generalized structural-parametric model of an electro magneto elastic converter for nano- and micrometric movement control systems: III. Transformation parametric structural circuits of an electro magneto elastic converter for nano- and micrometric movement control systems. Journal of Computer and Systems Sciences International. 2006;45(2):317‒325.
11. Afonin SM. Decision wave equation and block diagram of electro magneto elastic actuator nano- and microdisplacement for communications systems. International Journal of Information and Communication Sciences, 2016; 1(2):22‒29.
12. Afonin SM. Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. Ed. Parinov IA. Nova Science, New York, 2015; pp. 225‒242.
13. Afonin SM. A structural-parametric model of electroelastic actuator for nano- and microdisplacement of mechatronic system. Chapter 8 in Advances in Nanotechnology. Volume 19. Eds. Bartul Z, TrenorJ, Nova Science, New York,2017; pp. 259‒284.
14. Afonin SM. Electro magneto elastic nano- and microactuators for mechatronic systems. Russian Engineering Research. 2018;38(12):938‒944.
15. Afonin SM. Nano- and micro-scale piezomotors. Engin. Res. 2012;32(7-8):519‒522.
16. Afonin SM. Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers, Mechanics of Solids2007;42(1):43‒49.
17. Afonin SM. Stability of strain control systems of nano-and microdisplacement Piezo transducers. Mechanics of Solids. 2014;49(2):196‒207.
18. Afonin SM. Structural-parametric model electro magneto elastic actuator nano displacement for mechatronics. International Journal of Physics. 2017;5(1): 9‒15.
19. Afonin SM. Structural-parametric model multilayer electro magneto elastic actuator for nano mechatronics. International Journal of Physics. 2019;7(2):50‒57.
20. Afonin SM. Structural-parametric model of Piezo actuat or nano- and microdisplacement for nanoscience. AASCIT Journal of Nano science. 2017;3(3):12‒18.
21. Afonin SM. Solution wave equation and parametric structural schematic diagrams of electro magneto elastic actuators nano- and microdisplacement. International Journal of Mathematical Analysis and Applications. 2016; 3(4):31‒38.
22. Afonin SM. Structural-parametric model of electro magneto elastic actuator for nanomechanics. 2018; 7(1):1‒9.
23. Afonin SM. Structural-parametric model and diagram of a multilayer electro magneto elastic actuator for nanomechanics. Actuators. 2019; 8(3): 1‒14.
24. Afonin SM. Structural-parametric models and transfer functions of electro magneto elastic actuators nano- and microdisplacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics. 2016; 2(2):52‒59.
25. Afonin SM. Structural-parametric model of electro elastic actuator for nanotechnology and biotechnology. Journal of Pharmacy and Pharmaceutics. 2018; 5(1):8‒12.
26. Afonin SM. Design static and dynamic characteristics of piezoelectric nanomicrotransducers. Mechanics of Solids. 2010; 45(1):123‒132.
27. Afonin SM. Electro magneto elastic Actuator for Nanomechanics. Global Journal of Research in Engineering: A Mechanical and Mechanics Engineering. 2018;18(2):19‒23.
28. Afonin SM. Multilayer electro magneto elastic actuator for robotics systems of nanotechnology, Proceedings of the 2018 IEEE Conference EIConRus, 2018; pp. 1698‒1701.
29. Afonin SM. A block diagram of electro magneto elastic actuator nanodisplacement for communications systems. Transactions on Networks and Communications. 2018; 6(3):1‒9.
30. Afonin SM. Decision matrix equation and block diagram of multilayer electro magneto elastic actuator micro and nanodisplacement for communications systems, Transactions on Networks and Communications. 2019;7(3):11‒21.
31. Afonin SM. Condition absolute stability control system of electro magneto elastic actuator for communication equipment. Transactions on Networks and Communications. 2020; 8(1):8‒15.
32. Afonin SM. A Block diagram of electro magneto elastic actuator for control systems in nanoscience and nanotechnology, Transactions on Machine Learning and Artificial Intelligence. 2020; 8(4):23‒33.
33. Afonin SM. Optimal control of a multilayer electroelastic engine with a longitudinal piezo effect for nanomechatronics systems. Applied System Innovation.2020; 3(4):1‒7.
34. Afonin SM. Structural scheme actuator for nano research. COJ Rev& Res. 2020; 2(5):1‒3.
35. Afonin SM. Structural–parametric model electro elastic actuator nano- and microdisplacement of mechatronics systems for nanotechnology and ecology research. MOJ Ecology and Environmental Sciences. 2018; 3(5):306‒309.
36. Afonin SM. Electro magneto elastic actuator for large telescopes. Aeron Aero Open Access J. 2018; 2(5):270‒272.
37. Afonin SM. Condition absolute stability of control system with electro elastic actuator for nano bioengineering and microsurgery. Surgery & Case Studies Open Access Journal. 2019; 3(3): 307–309.
38. Afonin SM. Piezo actuators for nanomedicine research. MOJ App Bio Biomech. 2019; 3(2):56‒57.
39. Afonin SM. Frequency criterion absolute stability of electro magneto elastic system for nano and micro displacement in biomechanics. MOJ App Bio Biomech. 2019;3(6):137‒140.
40. Afonin SM. Multilayer Piezo engine for nanomedicine research. MOJ App Bio Biomech. 2020;4(2):30‒31.
41. Afonin SM. Multilayer engine for microsurgery and nano biomedicine. Surgery & Case Studies Open Access Journal.2020;4(4):423‒425.
42. Nalwa HS. Encyclopedia of Nanoscience and Nanotechnology. Los Angeles: American Scientific Publishers. 2004; 10 Volumes.