In this work we received the frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics. The aim of this work is to determine the frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics We used the frequency methods for Lyapunov stable control system to calculate the frequency criterion absolute stability of the control system with electromagnetoelastic actuator. In result we determined stationary set of the control system of the hysteresis deformation of the electromagnetoelastic actuator in form the segment of the straight line.

In this work the frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics is calculated. The control systems with electromagnetoelastic actuator on piezoelectric, electrostrictive and magnetostrictive effects solves problems of the precise matching in biomechanics, the compensation of the temperature and gravitational deformations of the equipment, the wave front correction in the adaptive laser system.¹⁻¹⁴ The piezoactuator for nano and micro displacement in biomechanics is used in the scanning tunneling microscope, the scanning force microscope, the atomic force microscope, in the gene manipulator.¹⁵⁻³¹ The problems of using criteria absolute stability of the control system with electromagnetoelastic actuator for nano and micro displacement in biomechanics are discussed. The stationary set of the control system of the deformation of the electromagnetoelastic actuator is received.

Characteristic deformation electromagnetoelastic actuator

In biomechanics the electromagnetoelastic actuator on piezoelectric, electrostrictive or magnetostrictive effects is used in the control systems for the micro and nano surgical repairs, the scanning tunneling microscopes, the micro and nano robotics, the micro and nano manipulators, the injectors.¹⁻⁶ The aim of this work is to receive the frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics, The measurements of the end face movement of the piezoactuator were made using Model 214 electronic measuring system of Caliber plant. The experimental static strain characteristic of the piezoactuator from PZT is shown in Figure 1. with the main hysteresis loops with the symmetrical voltage change and with special cycles with the asymmetric voltage change on the plates of the piezoactuator. We use the transfer function of the linear part of the systemand the hysteresis function of the relative deformationof the electromagnetoelastic actuator.¹⁶

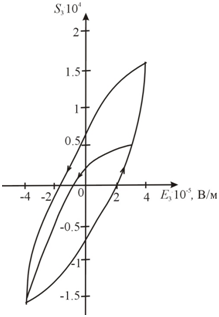
Figure 1 Hysteresis type characteristic deformation of piezoactuator from PZT for longitudinal piezoeffect with main and particular hysteresis loops.

where S_j is the relative displacement of the cross section of the actuator along j axis, Ψ_i is the control parameter of the actuator along i axis. The hysteresis function S_j at each time instant t depends on the behavior of the function Ψ_i = E_i or Ψ_i = H_i, where E_i and H_i are the electric field strength and the magnetic field strength on the interval [0,t], the value of t, the initial value S_j(0), and the sign of the rate Ψ′_i of the field strength variation.

We have hysteresis type characteristic of the deformation of the electromagnetoelastic actuator for nano biomedicine on Figure 1. The set S_j(0)is the vertical segment$\left[S_j^0,-S_j^0\right]$ bounded by the points of intersection of the ordinate axis with the hysteresis loop at the maximum admissible field strength in the actuator.

In static regime we receive the stationary set N for the deformation of the piezoactuator in control system on Figure 2 for the stable linear part of the control system. We have the equation for the straight line L

where $W_{ij}\left(0\right)$ is the static value of the transfer function of the linear part of the control system.

Figure 2 Hysteresis type characteristic deformation of piezoactuator in control system.

$E_i+{\text{W}}_{ij}\left(0\right)S_j=0$

We have the stationary set N of the system in the form the marked segment of straight line L in Figure 2. Each point of intersection of the hysteresis nonlinearity with the partial loops and the straight line L corresponds to one equilibrium position. Let us consider butterfly type characteristic of the deformation of the electromagnetoelastic actuator for nano and micro displacement in biomechanics. For the actuator with the electrostrictive effect the deformation characteristic on butterfly wings is observed for unipolar change of the electric field strength on Figure 3. We obtain the particular cycle on one wing of butterfly in the form of the hysteresis loop. For butterfly type characteristic deformation of actuator in the control system the coordinate origin is moved to new zero with top dash on Figure 3.

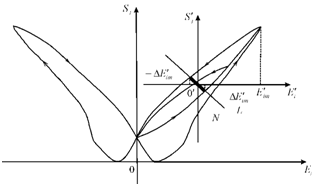
Figure 3 Butterfly type characteristic deformation of actuator with electrostrictive effect in control system.

We have for hysteresis loop on butterfly type characteristic the stationary set N of the control system marked segment of straight line L in Figure 3. For the magnetostrictive actuator the deformation characteristic has the butterfly type. We obtain the continuous function $S_j\left(E_i\right)$ of the hysteresis loop of the piezoactuator with the quantities of the derivative

${\nu }_{1ij}, {\nu }_{2ij}\in \left[0,{\nu }_{ij} \right],{\nu }_{ij}=\text{max}\left[\frac{\text{d}{S}_j}{\text{d}{E}_i}\right]$

where the quantities of the derivativeandare calculated using the hysteresis characteristic on Figure 1 for the maximum admissible electric field strength in the piezoactuator. The quantities  and  are the minimum and the maximum values of the tangent of the inclination angle of the tangent line to the hysteresis nonlinearity of the piezoactuator. We receive

${\nu }_{33}:{\nu }_{31}:{\nu }_{15}=d_{33}:d_{31}:d_{15}$

where the ratios of the tangents of the inclination angle of the tangent line to the hysteresis nonlinearity of the piezoactuator are proportional to the ratios of the piezomodules.

Frequency criteria absolute stability electromagnetoelastic system

The frequency methods for Lyapunov stable control system are used to determine the condition of the absolute stability of control system² with electromagnetoelastic actuator in biomechanics. We received the sufficient absolute stability condition of the electromagnetoelastic control system with the hysteresis nonlinearity of using the Yakubovich absolute stability criterion with the condition on the derivative. This criterion is the development of the Popov absolute stability criterion.² For the Lyapunov stable control system and the Yalubovich absolute stability criterion for the system with hysteresis provides the simplest and pictorial representation of results of the investigation of the stability of electromagnetoelastic system for nano and micro displacement in biomechanics.

We have the expression for the sufficient absolute stability condition of the system with the hysteresis nonlinearity of the electromagnetoelastic actuator using the Yakubovich absolute stability criterion with the condition on the derivative. The Yalubovich criterion is the development of the Popov absolute stability criterion.² For the Lyapunov stabile control system the Yalubovich absolute stability frequency criterion for the system with the single hysteresis provides the simplest and pictorial representation for the stability control system. The frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics at${\nu }_{1ij}=0$ and ${\nu }_{2ij}={\nu }_{ij}$ have the form

$\text{Re} {\nu }_{ij}{W}_{ij}\left(j\text{ω}\right)\ge -1$

where is the amplitude-phase characteristic of the open-loop system and in brackets j is the imaginary unity and  is the frequency.The amplitude-phase characteristic of the open-loop system ${\nu }_{ij}{W}_{ij}\left(j\text{ω}\right)$ on Figure 4 should be situated to the right of the straight line

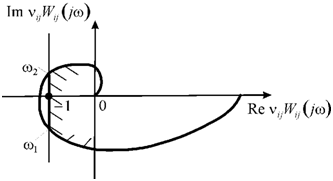
Figure 4 Absolute stability criterion of electromagnetoelastic system for nano and micro displacement, shaded corrected amplitude-phase characteristic.

$\text{Re} {\nu }_{ij}{W}_{ij}\left(j\text{ω}\right)=-1$

for all values of $\omega \ge 0$

Let us consider the frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics on the plane of the logarithmic amplitude frequency characteristic and the phase frequency characteristic

$L\left(\text{ω}\right)=Q\left[\text{φ}\left(\text{ω}\right)\right],L\left(\text{ω}\right)=20\text{lg}\left| {\nu }_{ij}{W}_{ij}\left(j\text{ω}\right)\right|$

We have the corrected logarithmic amplitude frequency characteristic below the boundary curve for electromagnetoelastic system of nano and micro displacement on Figure 5 in the form

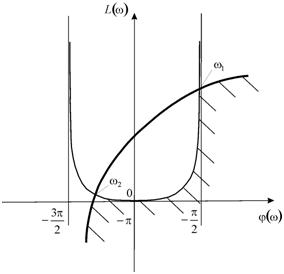
Figure 5 Absolute stability criterion of electromagnetoelastic system for nano and micro displacement, shaded corrected logarithmic amplitude frequency characteristic from phase.

$L\left(\text{ω}\right)=20\text{lg}\left| 1/\text{cosφ}\right|$

We obtained for the piezoactuator from PZT the value of the maximum tangent of the inclination angle of the tangent line to hysteresis nonlinearity about 1 nm/V for longitudinal piezoeffect and about 0.6nm/V for transverse piezoeffect. We used the frequency methods for Lyapunov stable control system to calculate the condition the absolute stability of the electromagnetoelastic system for nano and micro displacement in biomechanics.

We received the frequency criterion absolute stability of the electromagnetoelastic system for nano and micro displacement in biomechanics. We obtained the stationary set of the electromagnetoelastic system for nano and micro displacement in biomechanics. The stationary set of the electromagnetoelastic system is the segment of straight line for hysteresis or butterfly characteristic deformation of the actuator. We determined condition of the absolute stability on the derivative for the electromagnetoelastic system of nano and micro displacement in biomechanics.

The author declares that there is no conflict of interest.

1. Schultz J, Ueda J, Asada H. Cellular actuators. Oxford: Butterworth-Heinemann Publisher. 2017. p. 382.
2. Yakubovich VA. Popov's method and its subsequent development. European Journal of Control. 2002;8(3):200‒208.
3. Zhou S, Yao Z. Design and optimization of a modal-independent linear ultrasonic motor. IEEE Transaction on Ultrasonics, Ferroelectrics, and Frequency Control. 2014;61(3):535‒546.
4. Przybylski J. Static and dynamic analysis of a flextensional transducer with an axial piezoelectric actuation. Engineering Structures. 2015;84:140‒151.
5. Ueda J, Secord T, Asada HH. Large effective-strain piezoelectric actuators using nested cellular architecture with exponential strain amplification mechanisms. IEEE/ASME Transactions on Mechatronics. 2010;15(5):770‒782.
6. Karpelson M, Wei GY, Wood RJ. Driving high voltage piezoelectric actuators in microrobotic applications. Sensors and Actuators A: Physical. 2012;176:78‒89.
7. Afonin SM. Block diagrams of a multilayer piezoelectric motor for nano- and microdisplacements based on the transverse piezoeffect. Journal of Computer and Systems Sciences International. 2015;54(3):424‒439.
8. Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transduser. Doklady Physics. 2008;53(3):137‒143.
9. Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady Mathematics. 2006;73(2):307‒313.
10. Cady WG. Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. New York, London: McGraw-Hill Book Company. 1946. p. 806.
11. Mason W. Physical acoustics: Principles and methods. Vol.1. Part A. Methods and devices. New York: Academic Press; 1964. p. 515.
12. Zwillinger D. Handbook of differential equations. Boston: Academic Press; 1989. p. 673.
13. Afonin SM. Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and nanomaterials: Fundamentals, developments and applications. Journal of Applied Mechanical Engineering. 2015. p. 225‒242.
14. Afonin SM. A structural-parametric model of electroelastic actuator for nano- and microdisplacement of mechatronic system. Chapter 8 in Advances in nanotechnology. New York: Nova Science; 2017. p. 259‒284.
15. Afonin SM. Nano- and micro-scale piezomotors. Russian Engineering Research. 2012;32(7-8):519‒522.
16. Afonin SM. Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers. Mechanics of Solids. 2007;42(1):43‒49.
17. Afonin SM. Structural-parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. International Journal of Physics. 2017;5(1):9‒15.
18. Afonin SM. Structural-parametric model of piezoactuator nano- and microdisplacement for nanoscience. AASCIT Journal of Nanoscience. 2017;3(3):12‒18.
19. Afonin SM. Solution wave equation and parametric structural schematic diagrams of electromagnetoelastic actuators nano- and microdisplacement. International Journal of Mathematical Analysis and Applications. 2016;2016;3(4):31‒38.
20. Afonin SM. Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 2018;7(1):1‒9.
21. Afonin SM. Structural-parametric models and transfer functions of electromagnetoelastic actuators nano- and microdisplacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics. 2016;2(2):52‒59.
22. Afonin SM. Parametric block diagrams of a multi-layer piezoelectric transducer of nano- and microdisplacements under transverse piezoelectric effect. Mechanics of Solids. 2017;52(1):81‒94.
23. Afonin SM. Structural-parametric model of electro elastic actuator for nanotechnology and biotechnology. Journal of Pharmacy and Pharmaceutics. 2018;5(1):8‒12.
24. Afonin SM. A structural-parametric model of a multilayer electroelastic actuator for mechatronics and nanotechnology. Chapter 7 in Advances in nanotechnology. Bartul Z, Trenor J, editors, New York: Nova Science; 2019. p. 169‒186.
25. Afonin SM. Structural-parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 2019;8(3):1‒14.
26. Afonin SM. Electromagnetoelastic actuator for nanomechanics. Global Journal of Research in Engineering: A Mechanical and Mechanics Engineering. 2018;18(2):19‒23.
27. Afonin SM. Structural-parametric model multilayer electromagnetoelastic actuator nanodisplacement for nanomechatronics. International Journal of Physics. 2019;7(2):50‒57.
28. Afonin SM. Actuator for nano biomedical research. Biomedical Journal of Scientific and Technical Research. 2019;19(3):14300‒14302.
29. Afonin SM. Structural–parametric model electroelastic actuator nano–and microdisplacement of mechatronics systems for nanotechnology and ecology research. MOJ Ecology and Environmental Sciences.2018;3(5):306‒309.
30. Afonin SM. Electromagnetoelastic actuator for large telescopes. Aeronautics and Aerospace Open Access Journal. 2018;2(5):270‒272.
31. Bhushan B. Springer Handbook of Nanotechnology. Berlin, New York: Springer; 2004. p. 1222.