Characterization, drying and sorption isotherm of Tunisian tomato- experimental and mathematical investigation

doi:10.15406/mojfpt.2016.02.00044

MOJ

eISSN: 2381-182X

Food Processing & Technology

Research Article Volume 2 Issue 4

Characterization, drying and sorption isotherm of Tunisian tomato- experimental and mathematical investigation

Bilel Hadrich,¹

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Imen Kharrat,¹ Nebil Kchaou²

¹Biological Engineering Department, National School of Engineers of Sfax, University of Sfax, Tunisia
²MFAGPE Laboratory, National School of Engineers of Sfax, University of Sfax, Tunisia

Correspondence: Bilel Hadrich, Biological Engineering Department, National School of Engineers of Sfax, University of Sfax, BP 1173, 3038, Sfax, Tunisia

Received: April 29, 2016 | Published: June 20, 2016

Citation: Hadrich B, Kharrat I, Kchaou N. Characterization, drying and sorption isotherm of Tunisian tomato- experimental and mathematical investigation. MOJ Food Process Technol. 2016;2(4):136-143. DOI: 10.15406/mojfpt.2016.02.00044

Download PDF

Abstract

The composition of the Tunisian Tomato (TT) reflects a very important nutritional value. In fact, the TT is rich in fiber (42g/100g d.m.), protein (16.994g/100g d.m.) and also potassium (245mg/100g d.m.) which is an essential micronutrient for humans thanks to its role in reducing the risk of hypertension. This renders the TT one of the major sources of this important mineral nutrient. An experimental determination of TT’s sorption isotherm is carried out at 45 and 55°C using the method of saturated salt solutions. The sorption curves are then approximated by twelve empirical models. The Peleg model yields the best fitting for both temperatures and for des/adsorption phenomenon. Drying of TT slices is carried out at the same two temperatures: 45 and 55°C and two air velocities: 0.5 and 1.6m/s. The convective drying characteristics of TT slices are established in a pilot dryer to assess the effect of drying air conditions on drying kinetics. Also, twelve different drying models are tested and compared according to their standard error and correlation coefficients to fit TT drying curves. The Logarithmic model shows the best fitting for all drying curves on all tested conditions.

Keywords: tomato, drying kinetics, sorption isotherms, empirical models

Introduction

Drying activity of tomato is prominently at the branch of the tomato processing. Tunisia is a big producer of tomato with 1100 000 tons in 2013, it is ranked 18th globally and 6th at MIAPT countries (Mediterranean International Association of the Processing Tomato).¹ Dried tomato consumption is very low in Tunisia because it has been abandoned in favor of the canned though it is in the eating habits of Tunisians. Dried tomato production is mainly oriented towards export. Indeed, a remarkable evolution of tomato production shows an increasing request for the export of the dried tomatoes. However this activity must be better supervised and structured at the levels of drying techniques, the hygiene, the storage conditions and the quality, in order to continue the positive evolution and to conquer new markets. The optimization of the drying operation must meet two essential requirements which are restricted consumption of energy and preservation of the biological quality of the dried product.^2-4 We study in this work the sorption isotherms and the drying kinetics of tomato in order to contribute to the understanding of tomatoes drying.

Materials and methods

All analyzes were performed in triplicate and results are expressed as mean ± standard deviation.

Moisture content and water activity

The dry weight was determined by drying the sample at a temperature of 105°C until obtaining constant weight.⁵ The moisture content (kg/kg dry matter) is calculated by the following formula:

$X = \frac{m - m_{s}}{m_{s}}$

with m: mass of the wet sample (kg) before drying, ms: mass of dry sample (kg) after drying.

The dry matter content (g/100 g fresh weight) was determined by following formula:

$dry matter content = \frac{m_{s}}{m} \times 100$

The determination of water activity was established by NOVASINA apparatus (AW Sprint TH-500) at 25°C. Protein Total nitrogen was determined by the Kjeldahl method. Protein was calculated using the general factor (6.25).⁶ Ash and mineral compositions Ash was determined by the incineration of the sample in a muffle furnace at 550°C for 3 h.⁵ The residue was dissolved in HNO³ and the mineral constituents (Ca, Mg, Na, K, Zn, Cu and Fe) were analyzed, using an atomic absorption spectrophotometer (Analytikjena AAS Zeenit 700).⁵

Lycopene

The determination of the lycopene content was performed according to the method developed by.⁷

Ascorbic acid

The extraction of vitamin C (ascorbic acid) was performed with 20 ml of metaphosphoric acid (HPO³)ⁿ (10%) from 20 g of crushed tomatoes. After centrifugation (5000 rpm, 15 min), the obtained pellet was washed again with 20 ml of the metaphosphoric acid solution, the supernatant was recovered and adjusted with distilled water to 50 ml.⁸ The dosage of vitamin C was performed according to the titration method by 2,6-dichloro-phenol-indophenol (D.C.P.I.P).⁹

Fat content

Fat content was determined by the Soxhlet method, using petroleum ether as a solvent at 40 °C.⁵

Dietary fiber

Total, soluble and insoluble dietary fiber content was determined according to the enzymatic–gravimetric method.¹⁰

Sorption isotherms

The adsorption and desorption isotherms of tomato were determined at 45 and 55°C by using the static gravimetric method. Ten saturated salt solutions were prepared by dissolving an appropriate quantity of salt in distilled water.² Each salt solution was prepared in a glass jar of 1 liter with an insulating lid. Every glass jar was a quarter filled with a saturated salt solution. The jars were placed in an oven of a fixed temperature for 24h to be stabilized. Each jar provided a fixed relative humidity (RH) corresponding to a fixed water activity (a^w) for each temperature and salt concentration (Table 1). The mass transfer between the product and the surrounding ambience in the jar was assured by moisture vapor diffusion. Equilibrium was considered to be reached when the change in samples weight did not exceed 0.0001 g.

Experimental drying

The study of the convective drying kinetics of tomato was carried out using the pilot dryer presented in Figure 1. The used experimental apparatus is a closed loop. The air flow running in the test section is horizontal to the product surface. First, the tomatoes were washed with distilled water and then carefully cut into four quarters. After the setting rate of air flow, the controller starts to heat up to the setting temperature. The air flows into the dryer with the fan; it passes the electrical resistors where it is heated. Once the experimental conditions are stabilized, the sample to dry is placed on the support plate of a balance in the horizontal test section (Figure 1) to establish the drying operation. The drying kinetics were determined from the measurements of the weight variation of the samples over time. These measurements are made using a precision electronic balance digital display. The balance is linked to a computer, and equipped with a data output for the acquisition of the mass over time. The obtained raw results were treated using a Matlab program carried out in this work to eliminate any disturbance caused by air ventilation. This program is founded using the polynomial sliding protocol for 5 by 5 points. The Matlab program calculates also the drying rate. Then the reduced moisture content evolution $X_{r} = (X - X_{e q}) / (X_{0} - X_{e q})$ was presented versus time and the drying rate as a function of moisture content variation; with $X_{e q}$ : equilibrium moisture content calculated by desorption modelling; $X_{0}$ : initial moisture content. Experiments were investigated on two levels of air temperature (45 and 55°C) and two levels of air velocity (0.5 and 1.6 m/s).

Sorption isotherms and drying curves fitting

The fitting of sorption isotherms and drying curves allows describing the experimental curves with empirical and semi-empirical models and identifying many useful parameters. Twelve models were tested for fitting of sorption isotherms (Table 2) and twelve models for drying curves fitting (Table 3). Those are the most used models for fitting data of sorption isotherms and drying curves.

Model parameters are determined by minimizing the difference between the experimental and calculated data. The mathematical treatment boils down to the use of non-linear regression by the software Curve Expert 1.4. The ability of these equations to analyze experimental data is verified by two statistical terms: standard error (SE) and correlation coefficient (r). Indeed, the greatest values of r and the smallest values of SE are the criteria that justify the choice of the most suitable model for the description of experimental data.

Results and discussion

Chemical composition

Table 4 summarizes the chemical composition of fresh tomatoes. The water activity refers to the availability of water in organic products. A value close to unity (0.860) is associated with the formation of a liquid water film on the surface of the pores whose dimensions are greater than or of the order of micrometer. The water retained by capillary forces explains the non-storability to the state.^33,34 We note also that the tomato is rich in water: about 95% of the fresh matter which explains that the food is not very rich in calories (18-20 kcal/100 g).³⁵ Analysis of fresh tomatoes (Table 4) shows also that these are rich in soluble fiber and insoluble fiber. Indeed, total fibers have about the contents of (42 g/100g d.m.). Fresh tomato is low in fat and cholesterol-free, and has average protein content about 17 g/100g d.m. This has been well noted by.³⁵ A grade of ascorbic acid content (1.616 g/100 g d.m.) shows the richness of the tomatoes in vitamin C.

Table 5 shows the mineral composition of fresh tomatoes. The tomato contains many minerals like most fruits and vegetables; it brings about a lot of potassium (245 mg/100 g d.m.) which is an essential micronutrient for humans and it can reduce the risk of hypertension which made her a significant source of this important mineral.³⁵ The obtained chemical and mineral compositions of fresh tomatoes are in the same order of obtained values by an anterior work for tomatoes by-product.³⁶

Figure 1 Dryer System.

Salt	NaOH	LiCl	MgCl₂	K₂CO₃	NaBr	SrCl₂	NaNO₃	NaCl	KCl	BaCl₂
45°C	0.0622	0.1112	0.3112	0.4157	0.5195	0.61	0.6999	0.7493	0.8174	0.89
55°C	0.053	0.1097	0.2993	0.4008	0.5015	0.5465	0.6815	0.7477	0.8070	0.8776

Table 1 Water activities of used saturated salt solutions at 45 and 55°C²

Model	Equation
GAB¹¹	$X_{e q} = \frac{X_{m} \cdot A \cdot B \cdot a_{w}}{(1 - B \cdot a_{w}) \cdot (1 - B \cdot a_{w} + A \cdot B \cdot a_{w})}$
BET¹²	$X_{e q} = \frac{X_{m} \cdot A \cdot a_{w}}{(1 - a_{w}) \cdot (1 + (A - 1) \cdot a_{w})}$
Modified BET¹³	$X_{e q} = \frac{A}{1 - B \cdot a_{w}}$
Halsey¹⁴	$X_{e q} = {(- \frac{A}{\ln (a_{w})})}^{1 / B}$
Oswin¹⁵	$X_{e q} = A \cdot {(\frac{a_{w}}{1 - a_{w}})}^{B}$
White and Eiring¹⁶	$X_{e q} = \frac{1}{A + B \cdot a_{w}}$
Adam & Shove¹⁷	$X_{e q} = A + B \cdot a_{w} + C \cdot a_{w}^{2} + D \cdot a_{w}^{3}$
Iglesias & Chirife¹⁸	$X_{e q} = A + B \cdot (\frac{a_{w}}{1 - a_{w}})$
Caurie¹⁶	$X_{e q} = \exp (A + B \cdot a_{w})$
Smith¹⁹	$X_{e q} = A - B \cdot \ln (1 - a_{w})$
Chung & Pfost²⁰	$X_{e q} = - \frac{1}{A} \cdot \ln (- \frac{T \cdot \ln (a_{w})}{B})$
Peleg²¹	$X_{e q} = - \frac{1}{A} \cdot \ln (- \frac{T \cdot \ln (a_{w})}{B})$

Table 2 Tested models for sorption isotherms fitting

Model	Equation
Newton²²	$X_{r} = \exp (- a \cdot t)$
Henderson & Pabis²³	$X_{r} = a \cdot \exp (- b \cdot t)$
Modified Henderson & Pabis²⁴	$X_{r} = a \cdot \exp (- b \cdot t) + c \cdot \exp (- d \cdot t) + e \cdot \exp (- f \cdot t)$
Logarithmic²⁵	$X_{r} = a \cdot \exp (- b \cdot t) + c$
Two terms²⁶	$X_{r} = a \cdot \exp (- b \cdot t) + c \cdot \exp (- d \cdot t)$
Two terms-exponential²⁷	$X_{r} = a \cdot \exp (- b \cdot t) + (1 - a) \cdot \exp (- b \cdot a \cdot t)$
Diffusional approach²⁵	$X_{r} = a \cdot \exp (- b \cdot t) + (1 - a) \cdot \exp (- b \cdot c \cdot t)$
Verma et al²⁸	$X_{r} = a \cdot \exp (- b \cdot t) + (1 - a) \cdot \exp (- c \cdot t)$
Page²⁹	$X_{r} = \exp (- a \cdot t^{b})$
Modified Page³⁰	$X_{r} = \exp ({(- a \cdot t)}^{b})$
Midilli-Kucuk³¹	$X_{r} = a \cdot \exp (- b \cdot t^{c}) + d \cdot t$
Wang and singh³²	$X_{r} = 1 + a \cdot t + b \cdot t^{2}$

Table 3 Tested models for drying curves fitting

Compound	Content
a_w	0.860 ± 0.003
Moisture content (%)	94.336 ± 0.010
Protein	16.994 ± 1.166
Lycopene	0.086 ± 0.005
Ascorbic acid	1.575 ± 0.059
Fat	1.123 ± 1.156
Insoluble fiber	31.22 ± 0.003
Soluble fiber	10.12 ± 0.003
Ash	8.691 ± 0.744

Table 4 Chemical composition of fresh tomatoes (g/100g d.m.)

Mineral	Content
Sodium	5.18 10^-2 ± 0.007
Potassium	245 ± 0.006
Magnesium	5.07 10^-2 ± 0.004
Calcium	9.037± 0.455
Iron	2.85 10^-2 ± 0.004
Zinc	3.98 10^-3 ± 0.002
Manganese	7.51 10^-3 ± 0.004

Table 5 Mineral composition of fresh tomatoes (mg/100 g d.m.)

Sorption isotherms and modelling results

Figure 2 shows the variation of equilibrium moisture content (X^eq) of tomato slices depending on a^w for the adsorption and desorption isotherms for 45°C. As seen, the sorption isotherms in tomatoes have a sigmoid shape of type II according to the BET classification,¹² as for most food. This type of isotherm is characterized by an asymptotic behavior in the field of high a^w in which water behaves like pure water. By wearing the adsorption isotherms and desorption of water from tomatoes on the same graph (Figure 2), we find that the adsorption curve does not overlap with the desorption one. This not even minimal coincidence is called hysteresis phenomenon. Most often, the isotherm of adsorption is lower than that of the dehydration. Same behaviors are observed for 55°C and all values of equilibrium moisture content for adsorption and desorption for the same a^w value, are lower than obtained for 45°C because of temperature effect (results not shown). The same form of desorption isotherm was obtained previously by³⁷ for other temperatures.

Table 6 shows a comparison between models used for modelling the adsorption and desorption isotherms for 45°C and 55°C. All models show a very important quality (r > 0.89 and SE < 0.13). Peleg model has the highest correlation coefficient (0.997 < r < 1) and the lowest standard error (0.006 < ES < 0.119) in the case of both adsorption and desorption isotherms for 45 and 55°C. Table 7 shows identified parameters of Peleg model for desorption and adsorption isotherms. Figure 2 shows also fitting results using Peleg model versus experimental one. In this work Peleg model is chosen for modelling the sorption isotherm for tomato at 45 and 55°C.

Drying curves and kinetics

The initial moisture content (X⁰) of tomatoes varies from 16.655 to 17.349 kg/kg d.b. and was decreased to a final moisture content ranging from 0.625 to 0.048 kg/kg d.b. The curves of the reduced moisture content as a function of time (Xr = f(t)) and the drying rate versus moisture content at the tested temperatures and air velocities are shown in Figure 3. The shape of the drying kinetics of tomato is similar for all tested temperatures and velocities. The moisture content of the product decreases rapidly in the first drying time, then more and more slowly in long time. Indeed, at the start of drying, the moving mechanism of water through the walls capillarity pores of the solid to the surface is obtained in an accelerated manner reflecting a rapid decrease in the water activity of the product. At the end of the drying process, product temperature increase at the center and the decrease of its moisture content lead to a new state of equilibrium in the product; a balance wherein the enthalpy difference between air temperature and product is reduced and solid water activity is equal to the relative humidity of the air. In this equilibrium, the water migrates therefore more hardly in the product and the internal transfer of matter becomes a limiting phenomenon. Other phenomenon are added and make the transfer difficult in the material such as the solute concentration, the growing phenomenon of crusting and the product surface hardening, reflecting a possible resistance of the cell walls.³ According to Figure 3, the comparison of the curves shows that the increasing of air temperature from 45 to 55°C reduced the drying time. This fact is due to the increase of the osmotic pressure of the water in the product. Temperature has a greater effect on the tomato moisture content than the velocity of drying. The temperature has a higher influence at 55°C. We can therefore conclude that there is a negative correlation between temperature and drying time. These results are in agreement with others obtained for other temperatures^37,38 and other food products such as carrot, apple, beet pulp etc…^39,40 The comparison of kinetics obtained at the same temperature and three velocities shows that the drying is faster for the higher velocity.⁴¹ However, for a constant drying temperature 55°C, increasing the drying rate from 0.5 to 1.6m/s is a waste of energy since the increase of drying velocity has no effect on the moisture content as a function of time. Drying kinetics of tomato did not show a constant rate period. Therefore, the drying of tomato took place during the falling rate period.

The evolution of the reduced water content (X^r) versus time (t) for different temperatures and different velocities were fitted by several models proposed in the literature. Only models of Newton, Henderson and Pabis, Modified Henderson and Pabis, Logarithmic, Two terms and Wang show a best fitting for all curves. The relative standard error (SE) for all models is between 0.006 and 0.061 and the relative correlation coefficient r shows values ranging from 0.977 to 1 (Table 8). The better model shown best fitting for all conditions is Logarithmic model. It is characterized by the minimum SE (0.006 ≤ SE ≤ 0.017) and maximum r (0.998 ≤ r ≤ 1). Logarithmic model is then selected to describe the drying curves of tomato for temperature ranging from 45 to 55°C and velocity from 0.5 to 1.6 m/s. Figure 3 shows also the fitting quality of logarithmic model at two temperatures and two velocities. Table 9 shows the optimum logarithmic parameters for all conditions.

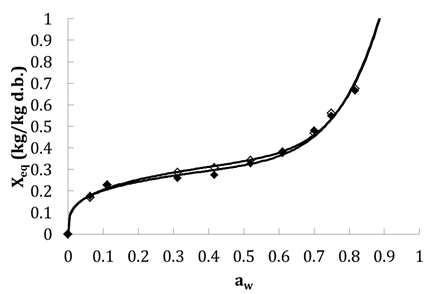
Figure 2 Fitted with Pelge model (-) and exprimental adsorption (solid motif) and desorption (empty motif) isotherms at 45°C.

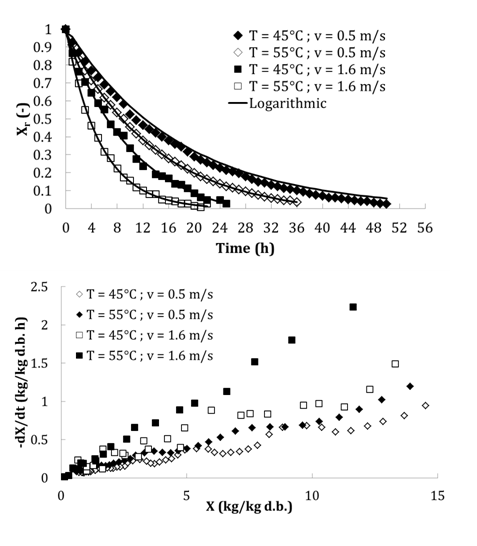
Figure 3 Drying kinetics at 45-55°C and 0.5-1.6 m/s. (a): Experimental reduced moisture content as function of drying time (points) and Logarithmic model (-); (b): drying rate as function of moisture content during drying.

Model	Type of sorption	45°C		55°C
Model	Type of sorption	r	SE	r	SE
GAB	Desorption	0.9948	0.0316	0.9994	0.00808
GAB	Adsorption	0.89676	0.13948	0.99598	0.01617
BET	Desorption	0.95823	0.08354	0.99742	0.01578
BET	Adsorption	0.96283	0.08027	0.99433	0.01809
Modified BET	Desorption	0.9766	0.06287	0.98991	0.03117
Modified BET	Adsorption	0.9803	0.0587	0.98056	0.0334
Halsey	Desorption	0.9901	0.04102	0.99958	0.00631
Halsey	Adsorption	0.99024	0.041	0.99445	0.0179
Oswin	Desorption	0.97843	0.0604	0.99735	0.01602
Oswin	Adsorption	0.97837	0.06145	0.99638	0.01446
White and Eiring	Desorption	0.9766	0.06287	0.98991	0.03117
White and Eiring	Adsorption	0.9803	0.0587	0.98056	0.0334
Adam and Shove	Desorption	0.99522	0.03236	0.99355	0.02828
Adam and Shove	Adsorption	0.99205	0.0424	0.99903	0.00851
Iglesias and Chirife	Desorption	0.96884	0.07241	0.99763	0.01512
Iglesias and Chirife	Adsorption	0.97423	0.06703	0.9849	0.02947
Caurie	Desorption	0.95413	0.08752	0.9875	0.03451
Caurie	Adsorption	0.957	0.08622	0.9973	0.01249
Smith	Desorption	0.96716	0.07391	0.96575	0.05681
Smith	Adsorption	0.9663	0.0765	0.98687	0.02749
Chung and Pfost	Desorption	0.9388	0.10625	0.89875	0.10182
Chung and Pfost	Adsorption	0.92574	0.11914	0.90141	0.07867
Peleg	Desorption	0.99785	0.02162	0.99936	0.00886
Peleg	Adsorption	0.99666	0.0275	0.99949	0.00621

Table 6 Statistical parameters of all tested models for sorption isotherms at 45 and 55°C

Temperature	Type of sorption	A	B	C	D
45°C	Desorption	0.408	0.296	1.578	7.91
45°C	Adsorption	0.373	0.266	1.566	7.328
55°C	Desorption	0.1067	0.3502	0.7183	4.288
55°C	Adsorption	0.2117	0.6691	1.377	7.739

Table 7 Optimum Peleg model parameters for desorption and adsorption isotherms

	T = 45°C v = 0.5 m/s		T = 55°C v = 0.5 m/s		T = 45°C v = 1.6 m/s		T = 55°C v = 1.6 m/s
Model	r	SE	r	SE	r	SE	r	SE
Newton	0.999	0.010	0.999	0.011	0.997	0.023	1.000	0.009
Henderson and Pabis	0.999	0.011	0.999	0.011	0.997	0.023	1.000	0.009
Modified Henderson and Pabis	0.999	0.011	0.999	0.011	0.997	0.026	1.000	0.010
Logarithmic	1.000	0.007	1.000	0.006	0.998	0.017	1.000	0.009
Two terms	0.999	0.011	0.999	0.011	0.997	0.025	1.000	0.009
Wang	0.991	0.037	0.993	0.033	0.993	0.034	0.977	0.061

Table 8 Statistical parameters of all tested models for drying curves

	T = 45°C ; v = 0.5 m/s	T = 55°C ; v = 0.5 m/s	T = 45°C ; v = 1.6 m/s	T = 55°C ; v = 1.6 m/s
a	1.014	1.019	1.046	0.999
b	0.057	0.074	0.095	0.188
c	-0.030	-0.037	-0.072	-0.003

Table 9 Optimum Logarithmic model parameters for all tested conditions

Conclusion

Desorption and adsorption isotherms of tomato were established using gravimetric method. The results show a sigmoid shape of type II according to the BET classification. Peleg model shows the best fit for sorption isotherms of tomato at 45 and 55°C. The optimum parameters of Peleg model are determined. Drying kinetics of tomato showed the absence of a constant rate period. Therefore, the drying of tomato took place during the falling rate period. The drying temperature has a greater effect on the tomato moisture content than the velocity. Logarithmic model shows the best fit for the drying curves obtained at different conditions (T = 45 and 55°C; v = 0.5 and 1.6 m/s). The optimum parameters of Logarithmic model are also presented.