Abstract
The analysis of planning the experiment of treated melon slices during the drying will help in decision of such matters as: creation of large powered equipments and effective methods of drying, automation of control and regulation of drying process.
Keywords: melon, osmotic drying, pulp thickness, concentration Mode
Introduction
The drying process of melons treated with sugar syrup studied using methods of optimal planning of full factorial experiment,1,2 which is described by the following equation:
The plan of the experiment (Table 1) is based on the basis of three factors in their natural dimensions (X1- concentration syrup within 70% and 50% -plus -minus x2 - product thickness 30mm and 10mm, plus or minus, x3 - drying method IR and convective convective plus minus.) in terms of dimensionless variables (x1, x2, x3).
The implementation of the plan prepared by the data presented in curves drying kinetics, melons, depending on the concentration (Figure 1), the thickness of the layer (Figure 2), the processing method. According to the results of experiments obtained by drying curves for different melon thermal effects (IR convection, convective).
№ |
Х1 |
Х2 |
Х3 |
Wн.срс |
Wкр.срс |
t1 (min) |
Nср |
t2 (min) |
Кср. |
1 |
+ |
+ |
+ |
62.4 |
47 |
75 |
0.3 |
285 |
0.075 |
2 |
+ |
+ |
- |
69.4 |
58 |
60 |
0.19 |
420 |
0.075 |
3 |
+ |
- |
+ |
59.5 |
50 |
30 |
0.32 |
300 |
0.118 |
4 |
+ |
- |
- |
59.5 |
52 |
45 |
0.17 |
435 |
0.084 |
5 |
- |
+ |
+ |
72.26 |
62 |
30 |
0.34 |
330 |
0.128 |
6 |
- |
+ |
- |
72.26 |
58 |
75 |
0.19 |
405 |
0.094 |
7 |
- |
- |
+ |
68.8 |
54 |
30 |
0.49 |
300 |
0.147 |
8 |
- |
- |
- |
68.8 |
58 |
45 |
0.24 |
435 |
0.108 |
Table 1 The plan of full factorial experiment in syrup
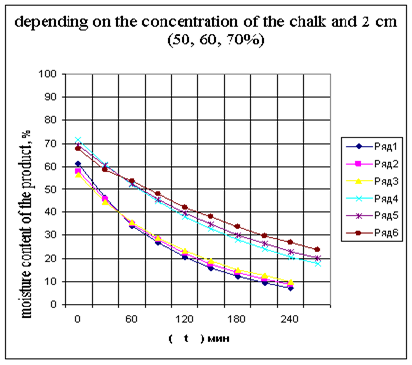
Figure 1 Where 1,2,3 ranks chopped pulp, 4,5,6 rows 2 cm thickness.
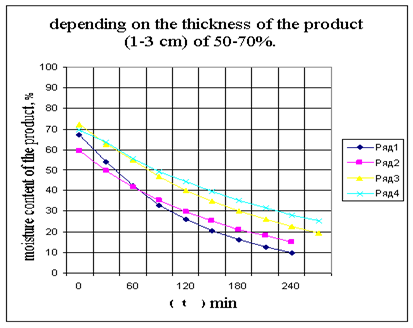
Figure 2 The number of the pulp treated with 1.3 to 50% syrup, 2.4 pulp is treated in a series of 70% syrup.
Drying curves consist of a constant speed period and falling rate drying period. Changing moisture in the first period is given by:
Here
For the second drying period we have:
Results and discussion
Changes in humidity melon pulp in a sugar syrup is determined by the formula:
Regression equations ratio drying melons during constant speed in the form
Straighten the curves obtained in the semi-logarithmic anamorphosis to determine the coefficient falling drying rate:
К= 0.283-0.0584Х1-0.0476Х2+0.0435Х3+0.0166Х1Х2-0.0116Х1Х3-0.0214Х2Х3+0.0008Х1Х2Х3
Conclusion
As a result, the planning of the experiment processed melon slices on drying obtained regression equation in times of permanent and falling rates of drying that allows us to choose the most appropriate methods for solving these problems.
Acknowledgements
Conflict of interest
The author declares no conflict of interest.
References
- Grachev Yu. Mathematical methods of planning experimented. Food Industry Handbook. 3rd ed. Moscow, Russia; 1979.
- Johnson N, Lyon F. Statistics and Planning of experiments in engineering and science. Mir. Moscow; 1981.

© . This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.



