MOJ
eISSN: 2381-182X


Action, the product of Energy times Time, a very interesting physical quantity has found application in fields of Physics such as Quantomechanics, the Planck constant having dimensions of Action. Well known is also the Principle of the Least Action followed by several phenomena in Physics and Chemistry. However, in other fields action has not found the attention, such an important concept deserves. In this paper, the concept of thermal action is coined in a suitable way so that applications are enabled in the field of Thermal Treatment of Foods. The obtained isodrastic curves following the analysis, describe the death kinetics of pathogenic bacteria with a potential application also in the field of the survival of probiotic bacteria in functional food products.
Keywords: action, death kinetics, thermal action, isodrastic curves
Food preservation techniques that are applied in food technology aim generally to reduce or prevent the growth of microorganisms in food.1-4 Pathogenic and spoilage bacteria, yeasts and molds can be destroyed or inactivated by the application of different preservation methods thermal or non-thermal.5-7 Thermal methods involve the heat treatment of foods applying different time/temperature combinations for different foods depending also on the targeted organisms. Some microorganisms are more heat resistant than others therefore require higher heat treatments to be inactivated. Non-thermal preservation techniques that can be applied include High Pressure Processing.8 Nowadays the food industry is constantly seeking ways to improve production efficiency and efficacy. Most of the companies in Europe and the USA follow accredited safety management systems monitoring and recording constantly time and temperatures. From heat treatment to freezing and cold storage, time and temperature are of critical importance not only to the safety of the final product but also to the quality. Consequently, it is clear that time and temperature and therefore Energy are of major importance to the food industry. In this report we propose the adaptation of a new term “Action” towards a more theoretical and fundamental approach in a field where the empiricism dominates until now. Action in science allows the use of analogies therefore having a broader applicability in a lot of nearby fields.
Action in Physics
Energy and Time play a significant role in Food Technology in general, particularly in Food Preservation, being the two main factors affecting the process (and/or unit operation), directly and indirectly, and the quality of the food product of the process indirectly. To name but a few, typical examples are the Death kinetics of the microorganisms,9,10 the relationship between freezing temperature and shelf life11 etc. The product Energy times Time, called Action, S, is one of the most important physical quantities and has initially been defined12 in the branch of Mechanics related with the motion of bodies, that is Dynamics. Action is defined as an integral of kinetic energy, KE, minus dynamic energy, DE, over time, from t1 to t2, as shown in equation (1).
Where, S is the action; KE is the Kinetic energy; DE is the Dynamic energy; dt is the time interval (t1-t2). Given a motion between two points, the path followed, tends to the minimization of S, leading to the famous Principle of Least Action , formulated as early as in 1756.13 Later on, the Planck constant, h, marking the appearance of a new evolutionary branch of Physics, namely Quantum mechanics, has been shown to have dimensions of action, whereas the dimensions of the reduced Planck constant, h bar are of angular momentum,14 as shown in equation (2).
………………………………….equation (2)
Where h is the Planck constant; h is the reduced Planck constant. Although Maupertois13 has meant a pretty general applicability of its Principle, the applications of that interesting and useful quantity, with a few exceptions in Chemistry15 and in Neuroscience,16 have never been extended to other practical fields, such as for example Food preservation which is the topic of the present paper. The classical approach followed in death kinetics is a totally empirical based in an array of concepts such as D, Z, F, L etc. This approach has been criticized by Paul Gibbs and one of us,10 proposing the water activity as a more fundamental property to describe the said above kinetics. Furthermore in the present paper a second step has been taken towards fundamental modeling that is the introduction of the concept of thermal action. Future work can combine the two important fundamental concepts, given that water activity is closely connected to the chemical potential which is also closely connected to Energy. Thus the water activity becomes the link between the classical empirical approach and the Action approach. The objective of the present paper is to explore the potential of application of the important physical quantity of Action, adapted for use in Food Microbiology and Food Preservation in general.
Definition of thermal action
The rationale for the definition of the quantity Thermal Action, is based on the fact that Time, t, and temperature, Θ are main factors influencing many phenomena in Food Technology and Preservation, upon thermal treatment. Temperature is dimensionally the concentration of heat that is of the thermal energy, under constant pressure, according to the dimensional analysis equation (3)
……………………………… equation (3)
Where Q: being the heat; ρ: the product of the density; Θ: Temperature; Cp: is the specific heat capacity
Since ρ. Cp remains a constant during many processes, temperature instead of heat could be used in the definition of Thermal Action. There is an overwhelming evidence that the effect of the temperature on the result of the thermal treatment is linear, whereas the effect of time is not linear but a logarithmic one (the logarithm with the base of ten is traditionally used). Therefore we coin the concept of Thermal Action SΘ as shown in equation (4).
……………………………………..equation (4)
In a plot of t versus Θ the obtained curves are, thus, isodrastic curves (from Δράσις, pronounced drasis, and the Greek word for Action). Furthermore in a plot of logt versus Θ the obtained isodrastic curves become parallel straight lines. Examples are given right below in the results and discussion section.
Application in death kinetics
Death kinetics is important to the Food scientist/technologist in a two-fold purpose. There are pathogenic or spoilage microorganisms, the population of which should be kept in a minimum, and on the other hand there are beneficial microorganisms the population of which should be protected. The study of their kinetic inactivation is useful in both cases. Clostridium botulinum is a pathogenic organism belonging to the first category mentioned above. In Figure 1 the isodrastic curves are shown based on raw data taken from literature.9 Each point in one of the curves is a pair of temperature and time values which were applied in the thermal treatment of the studied microorganism and yields the same degree of inactivation m. For example, m=12 shows the exponential degree of reduction of the microorganism’s population. If we start with an initial population of the microorganism in concern of 1012, only one individual microorganism will be left active. If instead of time, the decadic logarithm of time is in the Y-axis, the family of the isodrastic curves become parallel straight lines. Also, this result is shown in Figure 2, where the isodrastic lines concern degrees of inactivation m equal to 12, 9 and 6 respectively.

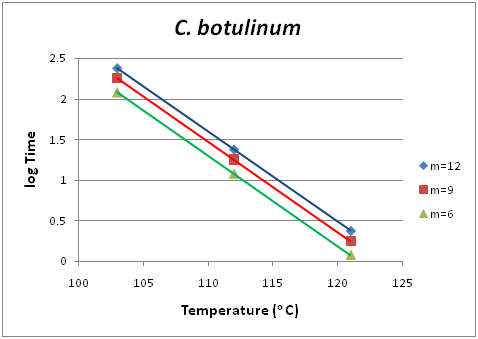
Analogous diagrams are shown for two more species of microorganisms, namely Bacillus stearothermophilus for low acidity foods of pH >4.5, Figure 3 and Figure 4 and Bacillus coagulans for acidic foods of pH <4.5, Figure 5 and Figure 6. The isodrastic curves are thus the loci of the points which are pairs of temperature and time values for which equivalent results are obtained in the reduction of the pathogenic microorganism. The chosen microorganisms of concern in this study are three bacteria that can cause serious effects on foods. Clostridium botulinum is a pathogenic microorganism that can cause foodborne botulism. Botulinum toxin can cause a severe flaccid paralytic disease in both humans and animals and therefore its absence from food must be verified. As a spore-forming bacterium it can survive conventional pasteurization heat treatments. To inactivate the spores pressurized heating is used to achieve temperatures above 100oC.17 Bacillus coagulansis a lactic acid-forming bacterial species that can cause coagulation in evaporated milk.18 Finally, Bacillus stearothermophilusis a thermophile and is widely distributed in soil, hot springs, ocean sediment, and is a cause of spoilage in food products.19 Apart from the application in death kinetics of pathogenic and spoilage microorganisms thermal action can also be applied when investigating the survival of probiotic bacteria in functional food products. Probiotic yogurts are products widely consumed nowadays in developed countries since people are getting more health conscious. The monitoring and survival of probiotics in yogurts has been well investigated over the past years. Several reports have been published showing that the initial population at start does not remain the same following storage at low temperatures.20,21 Using action we potentially aim at modeling the survival and death of the probiotic bacteria in an attempt to be in position to predict not only the conventional shelf life of the product, but most importantly its functional shelf life. The functional shelf life would be the period of time during which the numbers of the probiotic in concern will be sufficient enough to have an impact on the health of the consumer.
The methodology developed in this paper is an effort towards a more theoretical and fundamental approach in a field where the empiricism dominates until now. A first criticism of the empirical approach in Food microbiology, in Death kinetics in particular was the paper of Gibbs & Gekas2 considering water activity to be the physical property that has a direct implication for microbiological safety of food. Secondly, the developed herewith approach is a useful tool to the practical Food scientist and/or engineer who does not need to deal with the array of the empirical concepts D, Z, F, L, C and so on. However the empirical those parameters have been taken implicitely into account on constructing the Time vs Temperature diagrams of this paper. Thirdly, the general concept of the physical quantity of Action in Science, it allows the use of analogies and a broader applicability in a lot of nearby fields. Next to the death kinetics of pathogenic microorganisms thought field of application of the developed approach is the field of useful microorganisms such as the lactobacilli in probiotic foods. To continue, other methods of food preservation utilizing thermal energy, like freezing, or even other forms of energy such as high pressure, osmotic solutions, magnetic field, multiple obstacles could be considered.
None.
The author declares no conflict of interest.

© . This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.