The structural model of the nano piezoengine is determined for applied biomechanics and biosciences. The structural scheme of the nano piezoengine is obtained. For calculation nano systems the structural model and scheme of the nano piezoengine are used, which reflect the conversion of electrical energy into mechanical energy of the control object. The matrix equation is constructed for the nano piezoengine in applied biomechanics and biosciences.

Keywords: nano piezoengine, structural model, applied biomechanics and biosciences

The nano piezoengine based on the inverse piezoeffect is used for applied biomechanics and biosciences, nanomedicine, nanobiology, microsurgery. The nano piezoengine is provided for applied biomechanics and biosciences in scanning probe microscopy, interferometers and adaptive optics, actively dampen vibrations, deform mirrors and the work with the genes.^1–6

For calculation nano systems the structural model and scheme of the nano piezoengine are used, which reflect the conversion of electrical energy into mechanical energy of the control object.^6–19

Structural model

For calculation the nano piezoengine on Figure 1 is determined the inverse piezoeffect.^1–49

$S_i= d_{ mi} E_m+s_{ ij}^{ E} T_j$

here $d_{ mi},s_{ ij}^{ E},E_m,T_j,S_i$  are piezomodule, elastic compliance, strength electric field, strength mechanical field, relative deformation.

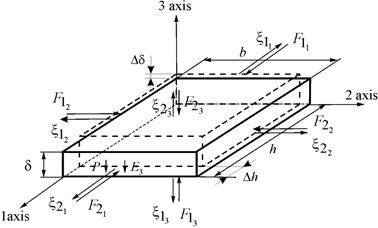
Figure 1 Nano piezoengine.

For the nano piezoengine the differential equation is evaluated^4–56

$\frac{d^2 \Xi \left(x,s\right)}{d{x}^2} - {\gamma }^2 \Xi \left(x,s\right)=0$

here $\Xi \left(x,s\right),x,s,\gamma$  are the transform of deformation, the coordinate, the parameter of transform, the factor of propagation.

For the longitudinal piezoengine at $x=0$  the deformation $\Xi \left(0,s\right)={\Xi }_1\left(s\right)$ , at $x=\delta ,\Xi \left(\delta ,s\right)={\Xi }_2\left(s\right)$  are calculated.

Its solution is written^4–36

$\Xi \left(x,s\right)=\left\{ {\Xi }_1 \left(s\right) \text{sh} \left[ \left(\delta -x\right) \gamma \right]+{\Xi }_2\left(s\right)\text{sh}\left(x\gamma \right)\right\}/\text{sh}\left(\delta \gamma \right)$

For the nano longitudinal piezoengine in Figure 1 its relative displacement on 3 axes^1–29 has the form

$S_3= d_{33} E_3+s{ }_{33 }^{ E} T_3$

The system for the nano longitudinal piezoengine is obtained^11–31 for $x=0,x=\delta$

$T_3\left(0,s\right)=\frac{1}{s{ }_{33}^{ E}} {\frac{d \Xi \left(x,s\right)}{dx} |}_{x=0}-\frac{d_{ 33}}{s{ }_{33}^{ E}}{E}_3\left(s\right)$

$T_3 \left(\delta ,s\right) = \frac{1}{s{ }_{33 }^{ E}} {\frac{d \Xi \left(x,s\right)}{dx} |}_{x=\delta }- \frac{d_{33}}{s{ }_{33 }^{ E}} E_3 \left(s\right)$

The structural model is evaluated for applied biomechanics and biosciences

$\begin{array}{l}{\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{\begin{array}{l} -F_1\left(s\right)+{\left( {\chi }_{33}^E \right)}^{ -1}\\ \times \left[\begin{array}{l} d_{33} E_3 \left(s\right)-\left[\gamma / \text{sh} \left( \delta \gamma \right) \right] \\ \times \left[\text{ch}\left( \delta \gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right] \end{array}\right\}\\ {\Xi }_2 \left(s\right) = {\left(M_2{s}^2\right)}^{-1} \left\{\begin{array}{l} - F_2 \left(s\right) + \left(\chi { }_{33}^{ E} \right){ }^{-1}\\ \times \left[\begin{array}{l} d_{33} E_3 \left(s\right) - \left[ \gamma / \text{sh} \left( \delta \gamma \right) \right]\\ \times \left[ \text{ch} \left( \delta \gamma \right) {\Xi }_2 \left( s \right) - {\Xi }_1 \left(s\right) \right] \end{array}\right] \end{array}\right\}\\ \chi { }_{33}^{ E} = s{ }_{33}^{ E} / S_0\end{array}$

here ${\Xi }_1\left(s\right),{\Xi }_2\left(s\right)$  - the transformations of displacements, $S_0$  - the area.

For the nano transverse piezoengine the expression of the transverse inverse piezoeffect^1–29

$S_1= d_{31} E_3+ s{ }_{11}^E T_1$

The system for the nano transverse piezoengine is determined for $x=0$  and $x=h$

$\begin{array}{l}{T}_1 \left(0,s\right)= \frac{1}{s{ }_{11}^E} {\frac{d \Xi \left(x,s\right)}{dx} |}_{x=0}- \frac{d_{ 31}}{s_{11}^{ E}} E_3 \left(s\right)\\ T_1 \left(h,s\right) = \frac{1}{s_{11}^E}{ \frac{d \Xi \left(x,s\right)}{dx} |}_{x=h}- \frac{d_{31}}{s_{11}^E} E_3 \left(s\right)\end{array}$

The structural model of the nano transverse piezoengine is calculated

$\begin{array}{l}{\Xi }_1 \left(s\right) = {\left( M_1{s}^2 \right)}^{-1} \left\{\begin{array}{l} - F_1 \left(s\right)+ {\left( \chi { }_{11}^{ E} \right)}^{-1}\\ \times \left[\begin{array}{l} d_{31} E_3\left(s\right) - \left[\gamma / \text{sh} \left( h\gamma \right) \right]\\ \times \left[\text{ch}\left(h\gamma \right) {\Xi }_1\left(s\right)- {\Xi }_2\left( s \right)\right]\end{array}\right] \end{array}\right\}\\ {\Xi }_{ 2} \left(s\right) = {\left( M_2 s^2 \right)}^{-1}\left\{\begin{array}{l} - F_2 \left(s\right) + \left( \chi { }_{11}^{ E} \right){ }^{-1}\\ \times \left[\begin{array}{l} d_{31} E_3\left(s\right)- \left[ \gamma / \text{sh} \left( h\gamma \right) \right]\\ \times \left[\text{ch}\left( h\gamma \right) {\Xi }_{ 2} \left( s \right)-\Xi { }_1 \left( s \right) \right] \end{array}\right] \end{array}\right\}\\ \chi { }_{11}^E = s{ }_{11 }^E/ S_0\end{array}$

For the nano shift piezoengine the expression of the shift inverse piezo effect^1–29

$S_5=d_{15} E_1+s{ }_{55}^{ E} T_5$

The system for the shift piezoengine is written at $x=0$  and $x=b$

$\begin{array}{l}{T}_5 \left(0, s\right)= \frac{1}{s{ }_{55}^{ E}} {\frac{d \Xi \left(x,s\right)}{dx} |}_{ x=0}- \frac{d_{ 15}}{s{ }_{55}^{ E}} E_1 \left(s\right)\\ T_5 \left(b,s\right)=\frac{1}{s{ }_{55}^{ E}}{\frac{d \Xi \left( x,s \right)}{ dx} |}_{ x=b} - \frac{d_{ 15}}{s{ }_{55}^E} E_1 \left(s\right)\end{array}$

The structural model is calculated

$\begin{array}{l}{\Xi }_1\left( s \right)= {\left( M_1 s^2 \right)}^{-1} \left\{\begin{array}{l} - F_{1 }\left( s \right)+ \left( \chi { }_{55}^{ E} \right){ }^{-1}\\ \times \left[\begin{array}{l}d{ }_{15} E{ }_1\left( s \right)- \left[ \gamma / \text{sh} \left( b \gamma \right) \right] \\ \times \left[\text{ch}\left(b\gamma \right){\Xi }_1\left( s \right)- \Xi { }_{2 }\left( s \right) \right]\end{array}\right] \end{array}\right\}\\ \Xi { }_{2 }\left( s \right)= \left( M_2{s}^2 \right){ }^{-1} \left\{\begin{array}{l} -F_2 \left( s \right)+ \left( \chi { }_{55}^E \right){ }^{-1}\\ \times \left[\begin{array}{l} d{ }_{15} E{ }_1 \left( s \right)- \left[ \gamma / \text{sh} \left( b\gamma \right) \right]\\ \times \left[\text{ch}\left( b\gamma \right){\Xi }_2\left(s\right)- \Xi { }_1 \left( s \right) \right] \end{array}\right] \end{array}\right\}\\ \chi { }_{55}^{ E} = s{ }_{55}^{ E} / S_{ 0}\end{array}$

At $x=0$  and $x=l$  for $l=\{\delta ,h,b$  the system in general is obtained

$\begin{array}{l}{T}_j\left(0,s\right)= \frac{1}{s_{ ij }^{\Psi }} {\frac{d \Xi \left(x,s\right)}{dx} |}_{x=0}- \frac{{\nu }_{ mi}}{s_{ ij }^{\Psi }} {\Psi }_m \left(s\right)\\ T_j\left(l,s\right)= \frac{1}{s_{ ij }^{\Psi }} {\frac{d \Xi \left(x,s\right)}{ dx } |}_{x=l}- \frac{{\nu }_{ mi}}{s_{ ij }^{\Psi }} {\Psi }_{m }\left(s\right)\end{array}$

The structural model and scheme of the nano piezoengine on Figure 2 are evaluated

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_{ 1 } \left(s\right)+\left(\chi { }_{ ij }^{ \Psi } \right){ }^{-1}\\ \times \left[\begin{array}{l}{\nu }_{ mi } {\Psi }_{ m }\left(s\right)-\left[ \gamma / \text{sh} \left(l\gamma \right) \right]\\ \times \left[\text{ch}\left(l\gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right] \end{array}\right\}$

${\Xi }_{ 2}\left(s\right)={\left(M_2 s^2\right)}^{-1}\left\{\begin{array}{l} -F_{ 2}\left(s\right)+\left(\chi { }_{ ij }^{\Psi } \right){ }^{-1}\\ \times \left[\begin{array}{l}{\nu }_{mi}{\Psi }_m\left(s\right)-\left[ \gamma / \text{sh} \left( l\gamma \right) \right]\\ \times \left[ \text{ch} \left(l\gamma \right){\Xi }_{ 2 }\left(s\right)-{\Xi }_{ 1 }\left(s\right)\right]\end{array}\right]\end{array}\right\}$

$\chi { }_{ij}^{\Psi } = s{ }_{ij}^{\Psi } / S_0$

$v{ }_{mi} = \{\begin{array}{c} d_{ 33 }, d_{ 31} , d_{ 15} \\ g_{ 33} , g_{ 31 }, g_{ 15 }\end{array}$

$\Psi { }_{m }= \{\begin{array}{c} E_{ 3 }, E_{ 3 }, E_{ 1 }\\ D_{ 3 }, D_{ 3}, D_{ 1} \end{array}$

$s{ }_{ ij }^{\Psi } = \{\begin{array}{c} s_{ 33 }^{ E }, s{ }_{ 11 }^{ E }, s{ }_{ 55 }^{ E }\\ s_{ 33 }^{ D },s{ }_{ 11 }^{ D }, s{ }_{ 55 }^{ D }\end{array}$

$\gamma =\{{\gamma }^E,{\gamma }^D$

$c^{ \Psi }=\{c^{ E},c{ }^D$

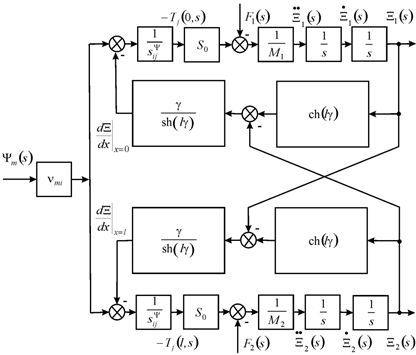
Figure 2 In general scheme of nano piezoengine.

The displacements matrix is calculated

$\left(\begin{array}{c}{\Xi }_1\left(s\right)\\ {\Xi }_2\left(s\right)\end{array}\right)=\left(\begin{array}{c}\begin{array}{ccc}{W}_{ 11 }\left(s\right)& W_{ 12 }\left(s\right)& W_{ 13 }\left(s\right)\end{array}\\ \begin{array}{ccc}{W}_{ 21 }\left(s\right)& W_{ 22 }\left(s\right)& W_{ 23 }\left(s\right)\end{array}\end{array}\right)\left(\begin{array}{c}{\Psi }_m\left(s\right)\\ F_1\left(s\right)\\ F_2\left(s\right)\end{array}\right)$

$W_{11}\left(s\right)={\Xi }_1\left(s\right)/{\Psi }_m\left(s\right)={{\nu }_{ mi} \left[M_2\chi { }_{ ij }^{\Psi } s^2+\gamma \text{th} \left(l\gamma /2\right)\right]/A}_{ ij }$

$A_{ ij }=M_1{M}_2{\left(\chi { }_{ ij }^{\Psi } \right)}^2{s}^4+\left\{\left(M_1+M_2\right){\chi }_{ ij }^{\Psi }/\left[c^{\Psi } \text{th} \left(l\gamma \right)\right]\right\} s^3+\left[\left(M_1+M_2\right)\chi { }_{ ij }^{\Psi } \alpha / \text{th} \left(l\gamma \right)+1/{\left(c^{\Psi }\right)}^2\right]s^2+2\alpha s/c^{\Psi }+{\alpha }^2$

$W_{ 21 }\left(s\right)={\Xi }_2\left(s\right)/{\Psi }_m\left(s\right)={{\nu }_{ mi }\left[M_1\chi { }_{ ij }^{\Psi }{s}^2+\gamma \text{th} \left(l\gamma /2\right)\right]/A}_{ ij }$

$W_{ 12 }\left(s\right)={\Xi }_1\left(s\right)/F_{ 1}\left(s\right)=-{\chi { }_{ ij }^{\Psi } \left[M_{ 2} \chi { }_{ ij }^{\Psi } s^2+\gamma / \text{th} \left(l\gamma \right)\right]/ A}_{ ij }$

$W_{ 13 }\left(s\right)={\Xi }_1\left(s\right)/F_{ 2}\left(s\right)=W_{ 22 }\left(s\right)={\Xi }_2\left(s\right)/F_{ 1}\left(s\right)=\left[\chi { }_{ ij }^{ \Psi }\gamma / \text{sh} \left(l\gamma \right)\right]/ A{ }_{ ij }$

$W_{ 23 }\left(s\right)={\Xi }_2\left(s\right)/F_{ 2 }\left(s\right)=-{\chi { }_{ ij }^{\Psi }\left[M_{1 } \chi { }_{ ij }^{\Psi } s^2+\gamma / \text{th} \left(l\gamma \right)\right]/ A}_{ ij }$

The static longitudinal displacements are evaluated

$\begin{array}{l}{\xi }_1=d_{ 33 } U M_{2 } / \left(M_1+M_2\right)\\ {\xi }_2=d_{ 33 } U M_{ 1 } / \left(M_1+M_2\right)\end{array}$

For $d_{ 33 }$  = $4\cdot {10}^{-10}m/V$ , $U$  = 25 V, $M_1$  = 1 kg, $M_2$  = 4 kg the static displacements ${\xi }_1$  = 8 nm, $${\xi }_2$$  = 2 nm and ${\xi }_1+{\xi }_2$  = 10 nm are evaluated at error 10%.

The equation of the direct piezo effect is used^1–29

$\begin{array}{l}D{ }_m= d_{mi} T_i + \epsilon { }_{mk }^{ E}{E}_{ k}\\ k_{ d}= \frac{d_{ mi }{S}_0}{\delta s{ }_{ij}^E}\end{array}$

here $\epsilon { }_{mk}^{ E},D_m,k_d$  - the permittivity, the electric induction and the direct coefficient. The transform the voltage of feedback for the nano piezoengine on Figure 3 is calculated

$U_d\left(s\right)=\frac{d{ }_{mi }{S}_0 R}{\delta s{ }_{ij}^E} {\stackrel{•}{\Xi }}_{{}_n} \left(s\right)= k_d R {\stackrel{•}{\Xi }}_{{}_n} \left(s\right),n=1,2$

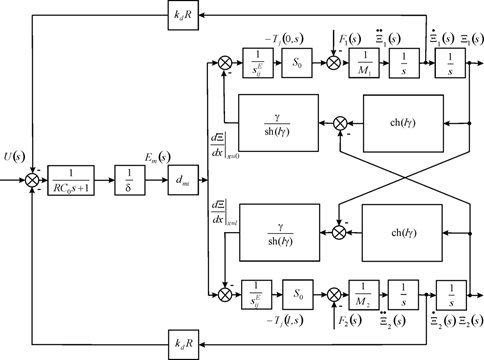
Figure 3 Scheme of nano piezoengine with back electromotive force.

For the nano piezoengine its static deformation is obtained.

For voltage control

$\begin{array}{l}{T}_{j\text{max}}= E_m d_{mi }/ s{ }_{ij}^E\\ F_{\text{max}}= E_{m } d_{ mi} S_{ 0 }/ s{ }_{ij}^E\end{array}$

For current control

$\begin{array}{l}{F}_{\text{max}}=\frac{U}{\delta } d{ }_{mi} \frac{S_{ 0}}{s{ }_{ij}^E}+ \frac{F{ }_{\text{max}}}{S_0} d_{ mi }S{ }_c \frac{1}{\epsilon { }_{mk}^{ T} S_{ c}/ \delta } \frac{1}{\delta } d_{ mi} \frac{S_{ 0}}{s{ }_{ij}^E}\\ \frac{F_{\text{max}}}{S_0} \left( 1- \frac{d{ }_{mi}^{ 2}}{\epsilon { }_{mk}^{ T} s{ }_{ij}^E} \right)s{ }_{ij}^E=E{ }_m d_{ mi }\\ T_{j\text{max} }\left( 1-k{ }_{mi}^{ 2} \right) s{ }_{ij}^E=E_{ m} d{ }_{mi}\\ k_{ mi} =d_{ mi }/\sqrt{ s{ }_{ij }^E \epsilon { }_{mk }^{ T}}\end{array}$

here $S_c,C_0,k_{ mi }$  - the sectional area of capacitor, the capacitance, and the coefficient of electromechanical coupling.

For current control of the nano piezoengine

$\begin{array}{l}{T}_{j \text{max}}=E{ }_m d_{ mi }/ s{ }_{ij}^D\\ F_{\text{max}}=E{ }_m d{ }_{mi} S_{ 0} / s{ }_{ij}^D\\ s{ }_{ ij }^{ D} = \left(1- k{ }_{ mi }^{ 2 }\right) s_{ ij }^{ E }\end{array}$

The mechanical characteristic of the nano piezoengine is obtained

$\begin{array}{l}\Delta l=\Delta l_{\text{max}}\left(1-F/F_{\text{max}}\right)\\ \Delta l_{ \text{max}}= \nu { }_{mi} {\Psi }_{ m }l\\ F_{\text{max}}=T_{j\text{ max}}{S}_0= \nu { }_{mi }\Psi { }_m S_{0 }/ s{ }_{ij }^{\Psi }\end{array}$

The expression of the mechanical characteristic of the nano transverse piezoengine is calculated

$\begin{array}{l}\Delta h=\Delta h_{\text{max}}\left(1-F/F_{\text{max}}\right)\\ \Delta h_{\text{max}}=d_{ 31 } E_{3}h\\ F_{ \text{max}}=d{ }_{3 1} E{ }_{3 }{S}_{ 0 }/ s{ }_{1 1}^{ E}\end{array}$

At $d_{ 3 1}$  = $2\cdot {10}^{-10}m/V$ , $E_3$  = 0.5∙10⁵ V/m, h = 2.5∙10^-2 m, $S_0$  = 1.5∙10^-5 m², $s{ }_{1 1}^E$  = 15∙10^-12 m²/N the parameters $\Delta h_{\text{max}}$  = 250 nm, $F_{\text{max}}$  = 10 N are obtained on Figure 4 at error 10%.

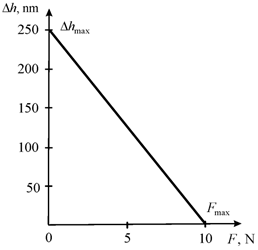
Figure 4 Mechanical characteristic of nano transverse piezoengine.

The deformation piezoengine at elastic load is obtained

$\begin{array}{l}\frac{\Delta l}{l} = \nu { }_{mi } {\Psi }_m- \frac{s{ }_{ij}^{\Psi } C_e}{S_0} \Delta l\\ F=C_e \Delta l\end{array}$

The control characteristic of the nano piezoengine is determined

$\begin{array}{l}\Delta l= \frac{{\nu }_{ mi } l {\Psi }_m}{1+ C{ }_{e }/ C_{ ij}^{ \Psi }}\\ s{ }_{ij } = k_{s }{s}_{ ij }^{ E},\left( 1- k{ }_{mi}^{ 2} \right)\le k_s\le 1\end{array}$

here $k_s$  the coefficients change of elastic compliance.

For the nano piezoengine its reverse and direct coefficients are calculated

$k_r=k_d= \frac{d_{ mi} S_0}{\delta s_{ ij }}$

By using the equation of load the scheme of the nano piezoengine with one fixed face on Figure 5 is calculated.

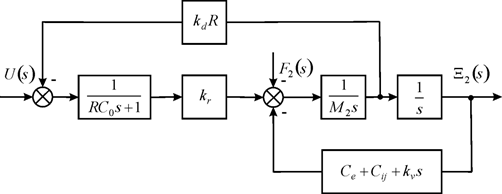
Figure 5 Scheme of nano piezoengine with one fixed face.

The expression on voltage for Figure 4 is calculated

$\begin{array}{l}W\left(s\right)={\Xi }_2\left(s\right)/U\left(s\right)=k_r/N\left(s\right)\\ N\left(s\right)=a_0 s^3+a_1 s^2+a_2 s+a_3\\ a_0=R C_0 M_2,a_1 =M_2+ R C_{0 } k_v\\ a_2=k_v+R C_0 C{}_{ij } + R C_{0 }C{}_e+ R k_{r }{k}_d,a_{ 3}= C{}_e + C{}_{ij }\end{array}$

here $k_v$  - the coefficient of damping.

For the nano transverse piezoengine for $R=0$  the expression on voltage is determined

$\begin{array}{l}W \left(s\right)= \frac{\Xi \left(s\right)}{U \left(s\right)}=\frac{k{ }_{31 }^{ U}}{T_t^2 s^2+2T_t {\xi }_t s+1}\\ k{ }_{31}^{ U} =d_{ 31 } \left(h/\delta \right)/\left( 1+C{ }_l/C{ }_{11}^{ E}\right)\\ T_t= \sqrt{M /\left( C{ }_l + C{ }_{1 1 }^{ E}\right)},{\omega }_t=1/ T_t\end{array}$

For $M$  = 2 kg, $C_l$  = $0.2\cdot {10}^{7}N/m$ , $C{ }_{11}^{ E}$  =$1.6\cdot {10}^{7}N/m$  the parameters $T_t$  = 0.33×10^-3 s, ${\omega }_t$  =$3 \cdot 10{ }^3 s{ }^{-1}$ are evaluated on Figure 6 at error 10%.

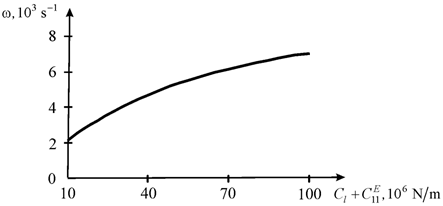
Figure 6 Bandwidth of nano transverse piezoengine.

The static displacement

$\Delta h=\frac{d_{ 31 }\left(h/\delta \right)U}{1+C_l /C{ }_{11}^{ E}}=k{ }_{31}^{ U} U$

For $d_{ 31}$  = $2\cdot {10}^{-10}m/V$ , $h/\delta$  = 24, $C_l /C{ }_{11}^{ E}$  = 0.1 the parameter $k{ }_{31}^{ U}$  = 4.4 nm/V is evaluated at error 10%.

For calculation nano systems the structural model and scheme of the nano piezoengine are used, which reflect the conversion of electrical energy into mechanical energy. The structural model and schemes of the nano piezoengine are obtained for applied biomechanics and biosciences. The matrix of the deformations of the nano piezoengine is constructed. The parameters of the nano piezoengine are determined for applied biomechanics and biosciences.

None.

None.

The authors declare that they have no conflict of interest.

1. Schultz J, Ueda J, Asada H. Cellular Actuators. Butterworth-Heinemann Publisher, Oxford. 2017:382p.
2. Afonin SM. Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Doklady Mathematics. 2006;74(3):943–948.
3. Uchino K. Piezoelectric actuator and ultrasonic motors. Boston, MA: Kluwer Academic Publisher. 1997:350p.
4. Afonin SM. Generalized parametric structural model of a compound elecromagnetoelastic transduser. Doklady Physics. 2005;50(2):77–82.
5. Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transducer. Doklady Physics. 2008;53(3):137–143.
6. Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady Mathematics. 2006;73(2):307–313.
7. Cady WG. Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. McGraw-Hill Book Company, New York, London. 1946:806p.
8. Mason W. Physical Acoustics: Principles and Methods. Vol. 1. Part A. Methods and Devices. Academic Press, New York. 1964:515p.
9. Yang Y, Tang L. Equivalent circuit modeling of piezoelectric energy harvesters. Journal of Intelligent Material Systems and Structures. 2009;20(18):2223–2235.
10. Zwillinger D. Handbook of Differential Equations. Academic Press, Boston. 1989:673p.
11. Afonin SM. A generalized structural-parametric model of an elecromagnetoelastic converter for nano- and micrometric movement control systems: III. Transformation parametric structural circuits of an elecromagnetoelastic converter for nano- and micrometric movement control systems. Journal of Computer and Systems Sciences International. 2006;45(2):317–325.
12. Afonin SM. Generalized structural-parametric model of an electromagnetoelastic converter for control systems of nano-and micrometric movements: IV. Investigation and calculation of characteristics of step-piezodrive of nano-and micrometric movements. Journal of Computer and Systems Sciences International. 2006;45(6):1006–1013.
13. Afonin SM. Decision wave equation and block diagram of electromagnetoelastic actuator nano- and microdisplacement for communications systems. International Journal of Information and Communication Sciences. 2016;1(2):22–29.
14. Afonin SM. Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. Ed. Parinov IA. Nova Science, New York. 2015:225–242.
15. Afonin SM. A structural-parametric model of electroelastic actuator for nano- and microdisplacement of mechatronic system. Chapter 8 in Advances in Nanotechnology. Volume 19. Eds. Bartul Z, Trenor J, Nova Science, New York. 2017:259–284.
16. Afonin SM. Electromagnetoelastic nano- and microactuators for mechatronic systems. Russian Engineering Research. 2018;38(12):938–944.
17. Afonin SM. Nano- and micro-scale piezomotors. Russian Engineering Research. 2012;32(7–8):519–522.
18. Afonin SM. Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers. Mechanics of Solids. 2007;42(1):43–49.
19. Afonin SM. Stability of strain control systems of nano-and microdisplacement piezotransducers. Mechanics of Solids. 2014;49(2):196–207.
20. Afonin SM. Structural-parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. International Journal of Physics. 2017;5(1):9–15.
21. Afonin SM. Structural-parametric model multilayer electromagnetoelastic actuator for nanomechatronics. International Journal of Physics. 2019;7(2):50–57.
22. Afonin SM. Calculation deformation of an engine for nano biomedical research. International Journal of Biomed Research. 2021;1(5):1–4.
23. Afonin SM. Precision engine for nanobiomedical research. Biomedical Research and Clinical Reviews. 2021;3(4):1–5.
24. Afonin SM. Solution wave equation and parametric structural schematic diagrams of electromagnetoelastic actuators nano- and microdisplacement. International Journal of Mathematical Analysis and Applications. 2016;3(4):31–38.
25. Afonin SM. Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 2018;7(1):1–9.
26. Afonin SM. Structural-parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 2019;8(3):1–14.
27. Afonin SM. Structural-parametric models and transfer functions of electromagnetoelastic actuators nano- and microdisplacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics. 2016;2(2):52–59.
28. Afonin SM. Design static and dynamic characteristics of a piezoelectric nanomicrotransducers. Mechanics of Solids. 2010;45(1):123–132.
29. Afonin SM. Electromagnetoelastic Actuator for Nanomechanics. Global Journal of Research in Engineering: A Mechanical and Mechanics Engineering. 2018;18(2):19–23.
30. Afonin SM. Multilayer electromagnetoelastic actuator for robotics systems of nanotechnology. Proceedings of the 2018 IEEE Conference EIConRus. 2018:1698–1701.
31. Afonin SM. A block diagram of electromagnetoelastic actuator nanodisplacement for communications systems. Transactions on Networks and Communications. 2018;6(3):1–9.
32. Afonin SM. Decision matrix equation and block diagram of multilayer electromagnetoelastic actuator micro and nanodisplacement for communications systems. Transactions on Networks and Communications. 2019;7(3):11–21.
33. Afonin SM. Condition absolute stability control system of electromagnetoelastic actuator for communication equipment. Transactions on Networks and Communications. 2020;8(1):8–15.
34. Afonin SM. A Block diagram of electromagnetoelastic actuator for control systems in nanoscience and nanotechnology. Transactions on Machine Learning and Artificial Intelligence. 2020;8(4):23–33.
35. Afonin SM. Optimal control of a multilayer electroelastic engine with a longitudinal piezoeffect for nanomechatronics systems. applied system innovation. 2020;3(4):1–7.
36. Afonin SM. Coded сontrol of a sectional electroelastic engine for nanomechatronics systems. applied system innovation. 2021;4(3):1–11.
37. Afonin SM. (2020) Structural scheme actuator for nano research. COJ Reviews and Research. 2020;2(5):1–3.
38.  Afonin SM. Structural–parametric model electroelastic actuator nano- and microdisplacement of mechatronics systems for nanotechnology and ecology research. MOJ Ecology and Environmental Sciences. 2018;3(5):306‒309.
39. Afonin SM. Electromagnetoelastic actuator for large telescopes. Aeronautics and Aerospace Open Access Journal. 2018;2(5):270–272.
40.  Afonin SM. Condition absolute stability of control system with electro elastic actuator for nano bioengineering and microsurgery. Surgery & Case Studies Open Access Journal. 2019;3(3):307–309.
41. Afonin SM. Piezo actuators for nanomedicine research. MOJ App Bio Biomech. 2019;3(2):56–57.
42. Afonin SM. Frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics. MOJ App Bio Biomech. 2019;3(6):137–140.
43. Afonin SM. Multilayer piezo engine for nanomedicine research. MOJ App Bio Biomech. 2020;4(2):30–31.
44. Afonin SM. Piezoengine for nanomedicine and applied bionics. MOJ App Bio Biomech. 2022;6(1):30–33.
45. Afonin SM. Multilayer engine for microsurgery and nano biomedicine. Surg Case Stud Open Access J. 2020;4(4):423–425.
46. Afonin SM. A structural-parametric model of a multilayer electroelastic actuator for mechatronics and nanotechnology. Chapter 7 in Advances in Nanotechnology. Volume 22. Eds. Bartul Z, Trenor J, Nova Science, New York. 2019:169–186.
47. Afonin SM. Electroelastic digital-to-analog converter actuator nano and microdisplacement for nanotechnology. Chapter 6 in Advances in Nanotechnology. Volume 24. Eds. Bartul Z, Trenor J, Nova Science, New York. 2020:205–218.
48. Afonin SM. Characteristics of an electroelastic actuator nano- and microdisplacement for nanotechnology. Chapter 8 in Advances in Nanotechnology. Volume 25. Eds. Bartul Z, Trenor J, Nova Science, New York. 2021:251–266.
49. Afonin SM. An absolute stability of nanomechatronics system with electroelastic actuator. Chapter 9 in Advances in Nanotechnology. Volume 27. Eds. Bartul Z, Trenor J, Nova Science, New York. 2022:183–198.
50. Afonin SM. Rigidity of a multilayer piezoelectric actuator for the nano and micro range. Russian Eng Res. 2021;41(4):285–288.
51. Afonin SM. Piezo engine for nano biomedical science. Open Access J Biomed Sci. 2022;4(5):2057–2059.
52. Afonin SM. An engine for nanochemistry. J Chem Appl. 2022;1(1):1–4.
53. Afonin SM. Electroelastic actuator of nanomechatronics systems for nanoscience. Chapter 2 in Recent Progress in Chemical Science Research. Volume 6. Ed. Min HS, B P International, India, UK. London 2023:15–27.
54. Afonin SM. Harmonious linearization of hysteresis characteristic of an electroelastic actuator for nanomechatronics systems. Chapter 34 in Physics and Mechanics of New Materials and Their Applications. Proceedings of the International Conference PHENMA 2021-2022, Springer Proceedings in Materials series. Volume 20. Eds. Parinov IA, Chang SH, Soloviev AN. Springer, Cham. 2023:419–428.
55. Shevtsov SN, Soloviev AN, Parinov IA, et al. Piezoelectric Actuators and Generators for Energy Harvesting. Research and Development. Springer, Switzerland, Cham. 2018:182 p.
56. Bhushan B. Springer Handbook of Nanotechnology. New York: Springer. 2004:1222.