Drying kinetics modeling and effective moisture diffusivity (D_eff) of osmotically dehydrated yellow sweet pepper (Capsicum annum L.) during microwave assisted convective drying at power levels of 70, 140, 210 and 280W, air temperature of 35, 45 and 60°C and constant air velocity of 1.5m/s were investigated. Among the 11 proposed models, Page model gave a better fit for all drying conditions used. D_eff decreased from 1.21x10^-7 to 8.91x10-8m²/s with decrease of drying temperature from 60 to 35°C which is 102 to103times reported earlier. The frequency factor (D₀) values decreased from 9.7564×10^-5 to 0.8806×10^-5m²/s while the activation energy of diffusion (E_a) decreased from 21.8741 to 10.7167KJ/mole with the increase in microwave power from 0.35 to 1.4W/g. So, pretreatment can be used as criteria for faster drying thereby maintaining final product quality. These mathematical models have much more practical utility as far as process design of food industry is concerned.

Keywords: m_icrowave drying, drying kinetics, moisture diffusivity, activation energy

Fruits and vegetables play a significant role in human nutrition as they provide many essential vitamins and minerals.¹ However, they are usually in shortage during off-seasons because of high perishability. A very common method of preservation for these agricultural corps is to dry them in order to reduce storage volume, minimizing packaging, storage, transportation costs and makes possible storage of the product under ambient temperatures and thereby extend their shelf life.^2‒4 Conventional drying involves exposure of food and agricultural products to high temperature and for long times, which can result in serious damage to flavor, color, rehydration capacity and nutrients of the treated material as well as low energy efficiency.^5‒8 However, in recentyears, microwave drying has gained popularity as an alternative drying method to overcome above problems for a wide variety of food products.^9‒11 It has several advantages over conventional hot air drying, such as higher drying rate, minimal heating at locations with less water, thus reducing overheating of atmosphere.¹² In microwave heating, as the temperature inside the material approaches the boiling point of water, pressure development becomes significant. This increase in vapour pressure facilitates the transfer of water to the outside¹³ and generates higher drying rates than conventional drying, where heat is transferred from the surface to the inside of the solids.^10,14‒16

M_icrowave drying system is widely used in combination with air drying system during drying via microwave energy.¹⁷ These combined drying systems not only increase the drying rate of the product, but also increase the quality of the dry product.¹⁸ Numerous studies were carried out with microwave-air combined dryers and many agricultural products have been dried successfully. Crops such as carrots,¹⁹ apple and mushroom^17,20 could be dried successfully using combined drying technique.

Peppers are an important source of nutrients in the human diet, and an excellent source of vitamin A and C as well as neutral and acidic phenolic compounds, which are important antioxidants for a variety of plant defense responses. However, heating causes losses of sensorial (texture, taste, flavor and color) and nutritional quality attributes, such as reduction of ascorbic acid content.²¹ Thus, to minimize the above losses, a study was conducted for the effect of the microwave-assisted drying on the characteristics of yellow sweet pepper. The overall goal of modeling a drying process is to understand and predict the influence of extrinsic factors such as temperature, contact time and pressure (vacuum) and intrinsic factors such as the nature of the food material, size and shape, on the mass transfer phenomena of moisture loss, color degradation, losses of bio-chemical parameters etc which influence the characteristics of the final product and hence its quality. Therefore, objectives of the present study are to compare the developed mathematical models for predicting the kinetics of drying, to investigate the drying rates and also the moisture diffusivity of yellow sweet pepper during combined microwave-convective drying as a function of the microwave power and air temperature.

Practical applications

The research findings of the study would give an innovative facet for food preservation and drying of yellow sweet pepper for enhancing the commercial potential of these commodities and open new avenues for food Industry. Modelling to application of microwave drying to food products which is part of a continuous from fresh foods to value added products manufacturing line helps to, calculate the residual moisture content of products as well as determination of diffusion rate and activation energy which saved the drying time on the basis of continuously generated data from univariate sensors. Next to monitoring, the application of continuous processes demands also real-time adjustment of critical input variables to ensure that the process stays within the design Space. M_echanistic models are very useful for this purpose as, once validated, several tools can be applied to gain further process knowledge, for example uncertainty and sensitivity analysis in large scale. Further, this article will help the researchers and academicians working in drying of agricultural commodities in general and yellow sweet pepper in particular.

Material

Fresh yellow sweet pepper samples were procured from the Center of Protected Cultivation Technology, Indian Agricultural Research Institute, New Delhi. The samples were washed and stored at 7±0.5°C in the cold storage until analysis. Before the drying experiments, the samples were taken out of the cold storage and sliced with a knife. At least 10 measurements of length, breadth and thickness were made at different points of the sliced pepper with a vernier caliper (M_itutoyo, Japan) having an accuracy of 0.02mm; only slices that fell within a 5% range of the average dimensions (length, breadth and thickness) were used. The average value of length (60±1.5mm) breadth (6±0.5mm) and thickness (4±0.41mm) were calculated. Initial moisture content was measured by taking 30g samples, dried in an oven at 70°C for 24h which was calculated as 89.01±0.45% (w.b.).²²

Pretreatment (osmotic dehydration)

The samples were osmotically dehydrated as a pretreatment using parameters, such as salt, sucrose, RPM, solution to sample ratio (SSR) and time, inside the incubator shaker by using Central Composite Rotatable Design (CCRD) given elsewhere.²³ These were optimized based on the objective requirements of weight loss, moisture loss and solid gain, and optimized dehydrated samples containing 71.29±0.65% (w.b.) moisture were taken for microwave drying.

Drying equipment and drying method

Drying experiments were performed in a laboratory scale microwave-convective dryer consists of four subsystems: air supply unit, heating unit, drying unit, and control unit, available in the Division of Post Harvest Technology, Indian Agricultural Research Institute, New Delhi. The blower (model: 0.24HP, 50Hz, continuous single phase) blows the air to the heating section to maintain the temperature up to desire level, regulated by thermostat from where it passes to the microwave oven. A thermostat (Multispan, MDC2901) was mounted over the blower to detect the change in the air temperature, which can be varied by manually using the regulator unit. The microwave oven (WP700L17.3 MW Oven, LG make, 17L Capacity) with technical features of ~230V, 50Hz, and 700W with a frequency of 2450MHz has the dimensions of 295, 458 and 370mm and consisted of a turn table of 270mm diameter at the base of the oven and it also operates in pulsed mode. The microwave oven has the capability of operating at ten different microwave output powers between 70 and 700W measured using the IMPI-2L test.²⁴ The adjustment of microwave power level and processing time was done with the aid of an analogue control facility located on the microwave oven. The dryer was run without the sample placed in, for about 30min to set the desired drying conditions before each drying experiment. Air velocity was measured with an hot wire anemometer (Model No: AM-4204; Make: LT Lutron, Taipei, Taiwan) having a least count of 0.1m/s. Preliminary experiments of microwave-hot air drying of yellow sweet pepper resulted in charring of the product towards the end of drying at power level higher than 280W. The combined microwave-hot air drying experiments were thus conducted with continuous microwave power of 280Wand step down intervals of 70W, in conjunction with hot air at 30, 45 and 60°C temperatures at constant air velocity of 1.5m/s.

Two hundred (200) grams of osmotically-dehydrated yellow sweet pepper was arranged in a single layer on the rotating glass plate and placed in the centre of the oven and the drying process was started for different combinations of microwave power and air temperature. Then, the samples were removed from the oven periodically and moisture loss was measured by weighing on the digital balance (Panacea GX 4000, Germany) with 0.01g precision. Three replications of each experiment were performed according to preset conditions and the data given are an average of these results. The reproducibility of the experiments was within the range of ±5%. Drying process continued until the moisture content of samples fell down to about 6% (w.b.). All weighing processes were completed in <10s during the drying process.

Theoretical consideration

Mathematical modeling of the drying curves: To determine the most suitable drying model, the drying cures were fitted to experimental data using eleven different thin layer drying models (Table 1). The moisture ratio and drying rate of yellow sweet pepper were calculated using the following equations:

$MR=\frac{M-M_e}{M_i-M_e}$  (1)

Where, MR is the moisture ratio, M is the moisture content at a specific time (kg/kg d.b.), M_i is the initial moisture content (kg/kg d.b.), and M_e is the equilibrium moisture content (kg/kg d.b.). The equilibrium moisture content was assumed to be zero for microwave drying as stated by Doymaz.²⁵ The MR, however, was simplified to M/M_i.

Drying rate = $\frac{M_{t+dt}-M_t}{dt}$ (2)

Where, M_t and M_t+dt are the moisture content (kg/kg d.b.) at drying time t and t+dt (min), respectively.

Effective moisture diffusivity

Generally, drying of foods takes place in two periods, a constant rate and falling rate period. After a short heating period, a constant rate period followed by a falling rate period which is a dominating period during drying process. The mechanism of moisture movement within a hygroscopic solid during the falling-rate period could be represented by effective moisture diffusion phenomenon (liquid diffusion, vapour diffusion, vaporization-condensation, hydrodynamic flow and other possible mass transfer mechanisms) is used and represents an overall mass transport property of water in the material. During drying, it can be assumed that diffusivity, explained with Fick’s diffusion equation, is the only physical mechanism to transfer the water to surface.²⁶ Effective moisture diffusivity, which is affected by composition, moisture content, temperature and porosity of the material, is used due to the limited information on the mechanism of moisture movement during drying and complexity of the process.²⁷ The effective moisture diffusivity D_eff, at any given moisture content can be determined using ‘methods of slopes’ technique.²⁸ Several researchers have utilized this technique for estimating the moisture diffusivity of food materials.^29‒31 So, Fick’s second law equation for non steady-state diffusion, assuming that the samples used can be approximated to cylinders, the diffusion is expressed by Crank.³²

$\frac{\partial M}{\partial t}=\frac{1}{r}\left\{\frac{\partial }{\partial r}\left(D_{eff}r\frac{\partial M}{\partial r}\right)+\frac{\partial }{\partial Z}\left(D_{eff}r\frac{\partial M}{\partial Z}\right)\right\}$  (3)

For the solution of Fick’s diffusion equation, the yellow sweet pepper slices were assumed as an infinite slab because of the thickness of the sample (4±0.4mm) was much less than its diameter. The effective moisture diffusivity for infinite slab was therefore calculated by the following solution.³²

$\frac{M-M_e}{M_0-M_e}=\frac{8}{{\pi }^2}{\displaystyle \sum _{}^{}{}_{n=0}^{\infty }}\frac{1}{{\left(2\text{n}+1\right)}^2}\text{x}\exp \left(-\frac{{\left(2\text{n}+1\right)}^2{\text{π}}^2{\text{D}}_{\text{eff}}}{4{\text{L}}^2}\text{t}\right)$  (4)

Where, D_eff is the effective diffusivity (m²/s); L₀ is the half thickness of slab (m). For long drying times; n=1, then Eq. (4) can be reduced to the following form:

$MR=\frac{8}{{\pi }^2}\exp \left(\frac{-{\pi }^2{D}_{eff}}{4L^2}t\right)$  (5)

Diffusivities are typically determined by plotting experimental drying data in terms of ln MR versus drying time t in Eq. (5), because the plot gives a straight line with a slope as follows:

$\ln MR=In\frac{8}{{\pi }^2}-\frac{{\pi }^2{D}_{eff}}{4L^2}t$   (6)

Slope = $\frac{{\pi }^2{D}_{eff}}{4L^2}$ (7)

Calculation of activation energy

The temperature dependence of the effective diffusivity may be described by an Arrhenius-type relationship^33‒35 as follows:

$D_{eff}=D_0\exp \left(\frac{E_a}{RT}\right)$  (8)

$\ln D_{eff}=\ln D_0-\frac{Ea}{RT}$  (9)

Plotting ln D_eff vs 1/T gives the slope of E_a/R to calculate the activation energy. Where, D₀ is the pre-exponential/Frequency factor of the Arrhenius equation (m²/s), E_a is the activation energy (J/mol), R is the universal gas constant (J/mol K), and T is the absolute temperature (K). From the slope of the straight line of ln D_eff versus reciprocal of T, described by the Arrhenius equation, the activation energy, E_a, could be calculated. The model described by equations (4) and (9) can be expressed in the simplified form:

 MR = f (T,t,L,D₀,E_a)

Where, t and T are variables and L, D₀ and E are the model parameters.

Statistical test

The non-linear regression procedure was used to obtain the drying parameters of the above equations using the MATLAB 7.1 (R2008a) software package. The coefficient of determination (R²) root mean square error (RSME) and residual sum of square (RSS) were used as primary criteria to select the best fit of the tested mathematical model to the experimental data. The higher the value of R² and lower the value of RSS and RSME, the better the model was taken to fit. By definition:

RSS=$\frac{{\displaystyle \sum _{}^{}{}_{i=1}^N\left(C_{exp,i}-C_{pre,i}\right)}}{N-P}$(10)

RMSE =$\sqrt{\frac{{{\displaystyle \sum }}_i^N{\left(C_{exp,i}-C_{pre,i}\right)}^2}{N}}a$ (11)

Where, C_exp,i is the i^th experimental value, C_pre,i is the i^th predicted value, N is the total number of observations, p is the number of constants in a particular model.

Drying kinetics

The moisture ratio versus drying time curves for microwave-convective drying of the osmotically dehydrated yellow sweet pepper samples (moisture content: 71.29±0.65%, w.b.) at different microwave output power levels (70, 140, 210 and 280W) and temperatures (30, 45 and 60°C) are shown in Figure 1. When the microwave power increased, the time needed to achieve a certain moisture ratio decreased being highest (122min) for 0.35W/g at 30°C and lowest (30min) for 1.4 W/g at 60 °C, which indicated that high power level saved 76% of the drying time for yellow sweet pepper to approximately 6% (w.b.) moisture content. Thus, it is obvious that the moisture ratio decreased more rapidly when the microwave power is increased. It was due to high electric field for high power, so that the rate of orientation of water molecules inside the heterogeneous food matrix were more causing more friction to be changed into heat for the evaporation of water molecules. Hence, the drying times were inversely proportional to applied microwave power levels applied. Similar observations were reported by Soysal³⁶ for parsley, Wang and Xi³⁷ for carrot slices, Giri and Prasad³⁸ for mushroom and Karaaslan and Tuncer³⁹ for spinach. However, Student’s t-test revealed that, keeping the power level constant, the moisture ratio had non- significant effect (p<0.05) with increase in air temperature from 30 to 60°C.

The relations between drying rate with drying time are shown in Figure 2. It was observed that with the increase in drying time the drying rate increased up to certain level with the increase in microwave power and air temperature and then gradually decreased. It was due to the fact that, after certain period, a small amount of water was present which required more time to drive out from the samples causing less drying rate. The maximum drying rate was 0.096 and 0.088 (g. water g. solid^-1.min^-1) for the samples. The initial moisture content of yellow sweet pepper was relatively constant (2.48g. water g. solid^-1), but the difference in the drying time requirements were mainly due to difference in the drying rate. The higher the power level, the greater the increase in drying rates. Nevertheless, a limit for power application was established on the basis of retaining the color stability of the product, otherwise browning may be detected due to sugar caramelisation by excessive local heating. Drying rate showed a fast increase at the beginning of the process due to microwave heating and a subsequent decrease, showing two differentiated periods: the first, where drying rate decreases slowly to reach a plateau with a practically constant value, and the second with a gradually decreasing drying rate from a given critical moisture content (Figure 3). So, drying rate curves showed a sigmoid shape, where the influence of microwave power can be observed practically in the entire range of sample moisture content. Nevertheless, at a higher power level, the initial rates are more greatly enhanced. The constant rate periods were more prominent at lower power level, being maximum at 0.7W/g and 30°C which gradually decreased with the increase in the power levels, being almost absent in 1.4W/g. It was because of thin layer of arrangement of samples and too rapid heating by high power, providing instant drying. The constant rate period ranged from 0.011 to 0.096g. Water g.solid^-1.min^-1 for the microwave output powers between 0.35 to 1.4W/g. After a short heating period, the time requirements during constant rate period varied with microwave output powers. The constant rate period was changed nearly from 1.84 to about 0.46g water g dry base^-1, nearly from 1.84 to about 0.56, nearly from 2.22 to about 0.28, nearly from 2.48 to about 0.21g water g dry base^-1 for the microwave output powers between 0.35 to 1.4W/g. A constant rate period was followed by a falling rate period in which moisture content decreased to 0.063g water g dry base^-1 for all drying conditions. These results were in agreement with the study of parsley leaves by Soysal³⁶ and spinach by Dadali et al.,²⁶ dried in a domestic microwave oven who reported that after a short heating period, a long constant rate period and a falling rate period was observed.

Modeling the thin layer drying data

The moisture content data obtained at different microwave powers and air temperatures were converted to the moisture ratio and then the curve-fitting procedure was performed for eleven well-known semi-empirical models in Table 1, among which Page model (Eq. 12) gave better fit for all drying data under all conditions tested with a higher R², less root mean square error (RMSE) and residual sum of square (RSS), shown in Table 2. The equation for Page model is,

$MR\left(k,n\right)=\frac{M-M_e}{M_o-M_e}=\exp \left(-k{t}^n\right)$  (12)

Where, k and n are empirical constant, t is the temperature.

Where, k and n are empirical constant, t is the temperature.

A good agreement was found between experimental and fitted values for yellow sweet pepper under all conditions. The parameters k and n of semi-empirical Page’s equation (Eq. 12) were estimated using nonlinear regression technique (Table 3) and the fitness is illustrated in Figure 1. From Table 3, the k value increases as the microwave output power increases during the drying process. Its values ranged from 0.016 to 0.102min^-1 and the model gave a better fit for all the experimental data points with R² greater than 0.98. As high R² and low RMSE and RSS values (<0.006) predicted for the sample, it is best suited for Page model. The best R² is 0.9992 for 1.4W/g microwave power at 30°C among all drying conditions. Based on the multiple regression analysis, the temperature dependence of the coefficients (k and n) was fitted to second order polynomial equation shown in Table 4.

Moisture diffusivity and activation energy

The results have shown that internal mass transfer resistance controls the drying time due to the presence of a falling rate drying period. Therefore, the values of effective diffusivity at different drying temperatures could be obtained by using Eq. 8. The average values of effective diffusivities in the drying process varied in the range of 1.21×10-7-8.91×10-8m²/s. As it is expected, the values of D_eff increased with the increase of drying temperature. Its values reached a maximum and then decreased as drying progresses. Diffusivity was not identifiable for moisture content values below 2.07kg/kg db for all conditions of microwave power and air temperature, is due to the hypotheses which impose equilibrium moisture content at the boundary on one hand and consider the migration of humidity depends on the parameters of drying air at the beginning of the process on the other hand.⁴⁰ However, the effective moisture diffusivities were 10² to 10³times more than the previous investigations for food materials which lie in range of 10^-11 to 10^-9m²/s.³³ The reason may be due to the effect of pretreatment (osmotic dehydration) where the texture and chemical constituents of the food were altered.⁴¹ during rotation inside the incubator-shaker which created different channeling paths for the water molecules to migrate outward resulting greater diffusivity by subsequent microwave drying. Hence, the pretreatment helped in enhancing the diffusion coefficient by which the drying time got reduced by faster removal the moisture and thereby the final product quality could be maintained. Effect of temperature on effective diffusivity is generally described using Arrhenius-type relationship (Eq. 8) to obtain better agreement of the predicted curve with experimental data. The frequency factor (D₀) and activation energy are shown in Table 5. The frequency factor (D₀) values decreased from 9.7564×10^-5 to 0.8806×10^-5m²/s while the activation energy decreased from 21.8741 to 10.7167KJ/mole with the increase in microwave power from 0.35 to 1.4W/g. The activation energy barrier must be overcome to activate moisture diffusion, and although it would be beneficial to use high temperatures so as to increase the drying rates by increasing moisture diffusion,⁴² it is advisable to dry yellow sweet pepper at optimum temperatures to maintain quality. The values of ln D_eff with inverse of temperatures are plotted (Figure 4), the slope of which gives the activation energy (Table 5). This activation energy is in reasonable agreement with the data presented by several other authors, for example 20.00KJ/mol for potato,⁴³ 27.61KJ/mol for corn,44 28.36KJ/mol for carrot.²⁵

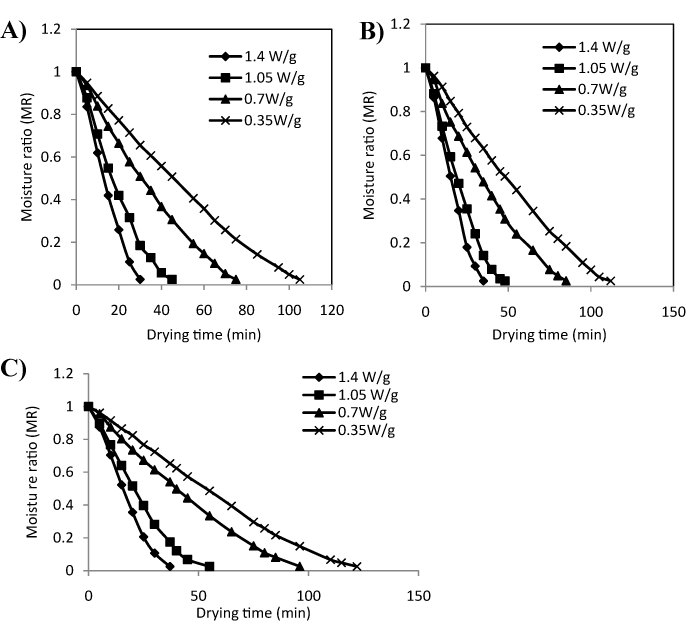
Figure 1 Effect of moisture ratio on drying time at different levels of power at air temperature of 60, 45 & 30 oC.

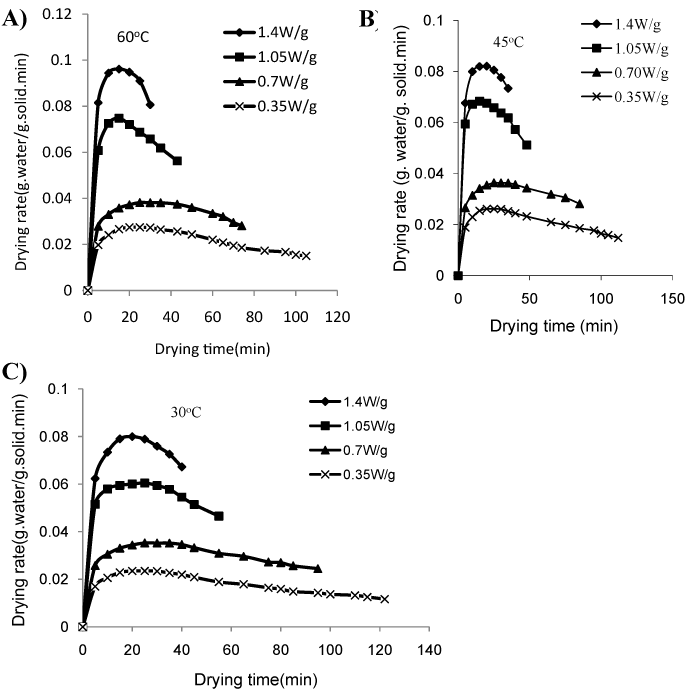
Figure 2 Effect of drying rate on drying time at different levels of power at air temperature of 60, 45 & 30 oC.

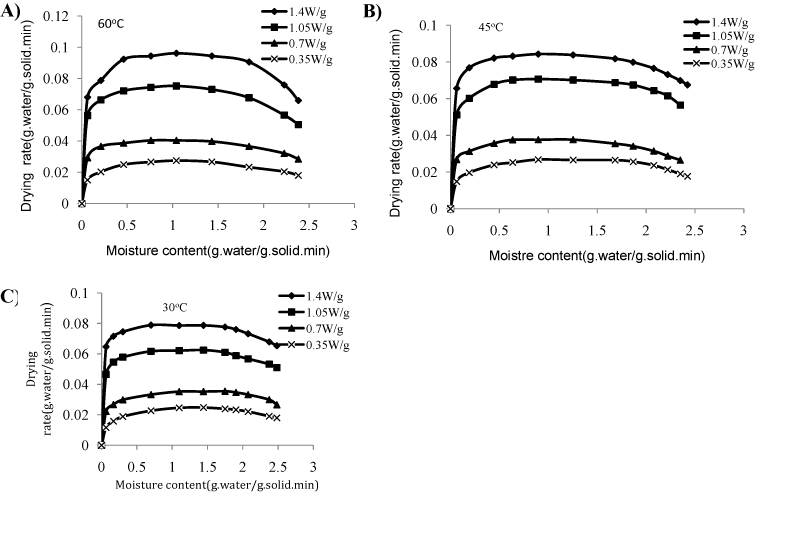
Figure 3 Effect of drying rate on moisture content at different levels of power at air temperature of 60, 45 & 30 oC.

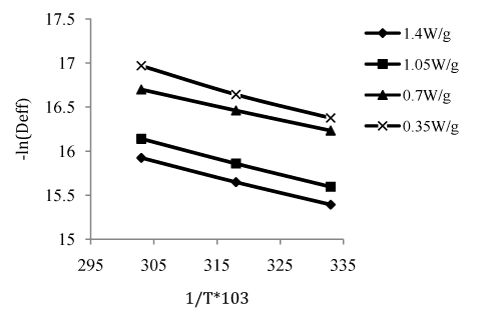
Figure 4 Arrhenius type relationship between effective moisture diffusivity and reciprocal of absolute temperature.

In order to explain the drying behaviour during microwave assisted convective drying of yellow sweet pepper, 11 different thin layer drying models were compared according to their R², RMSE and RSS. The relationships between the model parameters and the drying conditions for the computation of the moisture ratio in relation to drying time were determined and reported. According to the results of thin layer microwave drying of yellow sweet pepper, Page model could be used to predict the moisture content of the product at any time of drying process with high ability between drying air temperatures of 30 and 60°C at constant air velocity of 1.5m/s. The drying rate increased remarkably with the power output and temperature of the microwave-convective dryer where drying takes place in the falling rate period. The coefficients of this model and the apparent diffusion coefficient are the most important parameters in the moisture transfer, and they were found to be dependent on the temperature of the drying air. D_eff decreased from 1.21x10^-7 to 8.91x10^-8m²/s with decrease of drying temperature from 60 to 35°C which is 10² to10³ times more than the previous investigations for food materials (range of 10-11 to 10-9m²/s) can be better explained by the effect of pretreatment (osmotic dehydration) where the texture and chemical constituents of the food were altered during rotation inside the incubator-shaker which created different channeling paths for the water molecules to migrate outward resulting greater diffusivity by subsequent microwave drying. Hence, the pretreatment helped in enhancing the diffusion coefficient by which the drying time got reduced by faster removal the moisture and thereby the final product quality could be maintained. These mathematical models can be used for online quality prediction at any time having much more practical significance and can be recommended to food industry for process design. Therefore the above research findings would be very useful for drying of yellow sweet peppers which have special nutraceutical and pharmaceutical potential. However, quality of end product using this drying system needs to be studied

None.

Author declares that there is no conflict of interest.

1. Craig W, Beck L. Phytochemicals: health protective effects. Can J Diet Pract Res. 1999;60(2):78‒84.
2. Baysal T, Icier F, Ersus S, et al. Effects of microwave and infrared drying on the quality of carrot and garlic. Eur Food Res Technol. 2003;218:68‒73.
3. Kordylas JM. Processing and preservation of tropical and subtropical foods. London: Macmillan Education Ltd; 1991.
4. Nicoleti JF, Telis-Romero J, Telis VRN. Air-drying of fresh and osmotically pre-treated pineapple slices: fixed air temperature versus fixed temperature drying kinetics. Drying Technol. 2001;19(9):2175‒2191.
5. Drouzas AE, Tsami E, Saravacos GD. Microwave/vacuum drying of model fruit gels. J Food Eng. 1999;39(2):117‒122.
6. Lin TM, Durance TD, Scaman CH. Characterization of vacuum microwave, air and freeze dried carrot slices. Food Res Int. 1998;31(2):111‒117.
7. Vadivambal R, Jayas DS. Changes in quality of microwave-treated agricultural products-a review. Biosystems Eng. 2007;98(1):1‒16.
8. Yongsawatdigul J, Gunasekaran S. Microwave vacuum drying of cranberries, part I. energy use and efficiency. J Food Process Pres. 1996;20(2):121‒143.
9. Bouraoui M, Richard P, Durance T. Microwave and convective drying of potato slices. J Food Process Eng. 1994;17(3):353‒363.
10. Feng H, Tang J. Microwave finish drying of diced apples in a spouted bed. J Food Sci. 1998;63(4):679‒683.
11. Tulasidas TN, Raghavan GSV, Mujumdar AS. Microwave drying of grapes in a single mode cavity at 2450 MHz: drying kinetics. Drying Technol. 1995;13(8&9):1949‒1972.
12. Sharma GP, Prasad S. Effective moisture diffusivity of garlic cloves undergoing microwave-convective drying. J Food Eng. 2004;65(4):609‒617.
13. Goksu EI, Sumnu G, Esin A. Effect of microwave on fluidized bed drying of macaroni beads. J Food Eng. 2005;66(4):463‒468.
14. Bal LM, Kar A, Satya S, et al. Drying kinetics and effective moisture diffusivity of bamboo shoot slices undergoing microwave drying. Int J Food Sci Technol. 2010;45(11):2321‒2328.
15. Maskan M. Drying, shrinkage and rehydration characteristics of kiwifruits during hot air and microwave drying. J Food Eng. 2001;48(2):177‒182.
16. Oliveira MEC, Franca AS. Microwave heating of foodstuffs. J Food Eng. 2002;53(4):347‒359.
17. Andres A, Bilbao C, Fito P. Drying kinetics of apple cylinders under combined hot air-microwave dehydration. J Food Eng. 2004;63(1):71‒78.
18. Torringa EM, van Dijk EJ, Bartels PV. Microwave puffing of vegetables: modelling and measurements. In Proceedings of the 31st microwave power symposium. Manassas: International Microwave Power Institute; 1996. p. 16‒19.
19. Prabhanjan DG, Ramaswamy HS, Raghavan GSV. Microwave assisted convective air drying of thin layer carrots. J Food Eng. 1995;25(2):283‒293.
20. Torringa E, Esveld E, Scheewe I, et al. Osmotic dehydration as a pre-treatment before combined microwave-hot-air drying of mushrooms. J Food Eng. 2001;49(2‒3):185‒191.
21. Howard LR, Smith RT, Wagner AB, et al. Provitamin A and ascorbic acid content of fresh pepper cultivars (Capsicum annuum) and processed Jalapenos. J Food Sci. 1994;59(2):362‒365.
22. Swain S, Samuel DVK, Bal LM, et al. Modeling the microwave assisted drying process of osmotically pretreated red sweet pepper (Capsicum annum L.). Food Sci Biotech. 2012;21(4):969‒978.
23. Swain S, Samuel DVK, Bal LM, et al. Thermal kinetics of colour degradation of yellow sweet pepper (Capsicum annum L.) undergoing microwave assisted convective drying. Int J Food Prop. 2013.
24. Buffler CR. Microwave Cooking and Processing: Engineering Fundamentals for the Food Scientist. New York: Van Nostrand Reinhold; 1993. p. 157‒159.
25. Doymaz I. Convective air drying characteristics of thin layer carrots. J Food Eng. 2004;61(3):359‒364.
26. Dadali G, Demirhan E, Ozbek B. Microwave heat treatment of spinach: drying kinetics and effective moisture diffusivity. Drying Technol. 2007;25(10):1703‒1712.
27. Abe T, Afzal TM. Thin-layer infrared radiation drying of rough rice. J Agr Eng Res. 1997;67(4):289‒297.
28. Perry RH, Green DW, Maloney JO. Perry’s Chemical Engineers’ Handbook. 6th ed. New York: McGraw-Hill; 1984. p. 13‒20.
29. Karathanos VT, Villalobos G, Saravacos GD. Comparison of two methods of effective moisture diffusivity from drying data. J Food Sci. 1990;55(1):218‒231.
30. Sharma GP, Verma RC, Pankaj P. Mathematical modeling of infrared radiation thin layer drying of onion slices. J Food Eng. 2005;71(3):282‒286.
31. Zogzas NP, Maroulis ZB, Marinos-Kouris D. Moisture diffusivity data compilation in foodstuffs. Drying Technol. 1996;14(10):2225‒2253.
32. Crank J. Mathematic of Diffusion. 2nd ed. London: Oxford University Press; 1975. p. 267‒268.
33. Madamba PS, Driscoll RH, Buckle KA. The thin layer drying characteristics of garlic slices. J Food Eng. 1996;29(1):75‒97.
34. Ozdemir M, Devres YO. The thin layer drying characteristics of hazelnuts during roasting. J Food Eng. 1999;42(4):225‒233.
35. Sanjuan N, Lozano M, Garcia PP, et al. Dehydration kinetics of red bell pepper (Capsicum annuum L var Jaranda). J Sci Food Agric. 2003;83(7):697‒701.
36. Soysal Y. Microwave drying characteristics of parsley. Biosystems Eng. 2004;89(2):167‒173.
37. Wang J, Xi YS. Drying characteristic and drying quality of carrot using a two-stage microwave process. J Food Eng. 2005;68(4):505‒511.
38. Giri SK, Prasad S. Drying kinetics and rehydration characteristics of microwave-vacuum and convective hot-air dried mushrooms. J Food Eng. 2007;78(2):512‒521.
39. Karaaslan SN, Tuncer IK. Development of a drying model for combined microwave-fan-assisted convection drying of spinach. Biosystems Eng. 2008;100(1):44‒52.
40. Azzouz S, Guizani A, Jomaa W, et al. Moisture diffusivity and drying kinetic equation of convective drying of grape. J Food Eng. 2002;55(4):323‒330.
41. Roca E, Broyart B, Guillard V, et al. Predicting moisture transfer and shelf-life of multi domain food products. J Food Eng. 2008;86(1):74‒83.
42. Carbonell JV, Pinaga F, Yusa V, et al. The dehydration of paprika with ambient heated air and the kinetics of colour degradation during storage. J Food Eng. 1986;5(3):179‒193.
43. Bon J, Simal S, Rossello C, et al. Drying characteristics of hemispherical solids. J Food Eng. 1997;34(2):109‒122.
44. Tolaba MP, Suarez C. Simulation of the thin-layer drying of corn by means of the diffusional model. Lebensm Wiss Technol. 1988;21(2):83‒86.
45. Ayensu A. Dehydration of food crops using solar dryer with convective heat flow. Solar Energy. 1997;59(4‒6):121‒126.
46. Agrawal YC, Singh RP. Thin-layer drying studies on short grain rice. ASAE paper No. 77-3531, St. Joseph, MI; 1977.
47. White GM, Ross IJ, Ponelert R. Fully exposed drying of popcorn. Trans ASAE. 1981;24(2):466‒468.
48. Akpinar EK, Bicer Y, Cetinkaya F. Modeling of thin layer drying of parsley leaves in a convective dryer and under open sun. J Food Eng. 2006;75(3):308‒315.
49. Yaldiz O, Ertekin C, Uzun HI. Mathematical modelling of thin layer solar drying of sultana grapes. Energy. 2001;26(5):457‒465.
50. Wang CY, Singh RP. A single layer drying equation for rough rice. ASAE Paper No. 78-3001. St. Joseph, MI: ASAE; 1978.
51. Togrul IT, Pehlivan D. Modeling of drying kinetics of single apricot. J Food Eng. 2003;58(1):23‒32.
52. Verma LR, Bucklin RA, Endan JB, et al. Effects of drying air parameters on rice drying models. Trans ASAE. 1985;28(1):296‒301.
53. Sharaf-Elden YI, Blaisdell JL, Hamdy MY. A model for ear corn drying. Trans ASAE. 1980;23(5):1261‒1265.
54. Sacilik K, Elicin AK. The thin layer drying characteristics of organic apple slices. J Food Eng. 2006;73(3):281‒289.