The recent publications about inertial torques acting on spinning objects describe their physics by mathematical models. The several inertial torques are generated by the rotating mass which produces centrifugal, Coriolis forces, and the change in the angular momentum. The values of the inertial torques depend on the geometries of the spinning objects. The volumetric geometries of the objects request complex analytical processing of the expressions for the inertial torques. The analysis of the known publication related to the spinning sphere shows the expressions of inertial torques derived from errors in the mathematical processing of integral equations. The wrong limits of the integral equations that give incorrect values for the inertial torques of the spinning sphere present these errors. This manuscript presents the corrected mathematical model for the inertial torques generated by the rotating mass of the spinning solid and hollow sphere.

Keywords: inertial torques, gyroscope theory, spinning sphere

The textbooks and research publications describe the various designs of spinning machine parts and mechanisms in engineering. They circumscribe how rotating objects exhibit gyroscopic effects, which can be calculated using inertial forces and torques to determine the actual dynamic properties for mathematical models of their movements.^1,2 The rotating parts and components come in different shapes, such as discs, rings, cylinders, spheres, circular cones, paraboloids, propellers, etc. The texts also mention that inertial torques for simple designs can be calculated using known methods and equations, while more complex forms require new mathematical models.^3,4 The publications explain how to apply standard methods to compute inertial torques for various spinning objects encountered in engineering. They also suggest using a universal method for calculating inertial torques for unique designs.^5,6 The texts mention that researchers face challenges in applying these methods to derive inertial torques and mathematical models for the motions of different rotating objects. The textbooks of classical mechanics attract the attention of readers on gyroscope problems.^7,8 Gyroscopic effects remain as a problem for researchers who published numerous works and tried to find analytical and confirm practically.^9,10 The new generation tries to give answers to unsolved properties of spinning objects whose rotating masses produce the system of inertial torques that manifest gyroscopic effects.^11,12

In the field of engineering, all spinning objects exhibit gyroscopic effects resulting from their inertial torques. Numerous designs of gyroscopic devices produce inertial torques generated by their rotating masses, which should be calculated by the defined expressions.¹³ Rotating masses of objects with unique geometry are base for the analytical expressions of their inertial torque.¹⁴ The known publications related to the gyroscopic effects are confined by the use of the gyroscopic torque of the change in the angular momentum which does not solve all aspects of gyroscopic devices.¹⁵ The gyroscopic effects are more diverse and their unsolved problems of inertial torques solve numerical models. The modern tendency of intensification of processes in engineering requests accurate commuting and designs of the mechanisms and devices. This direction is important for the gyroscopic devices in which spinning components generate considerable inertial torques. The publications related to the theory of gyroscopic effects comprise a limited number of analytical approaches that do not satisfy engineering requirements.¹⁶ The new and original design of gyroscopic devices remains an unsolved problem and presents a challenge for researchers and practitioners because of the absence of mathematical models for the inertial torques.¹⁷ A known publication that comprises the inertial torques acting on a spinning sphere is presented by analytical errors in mathematical processing that yield incorrect solutions.¹⁸ The theory of gyroscopic effects for rotating objects opens a new direction in the dynamics of machines.¹⁹ The specificity of inertial torques generated by the rotating mass of spinning objects is presented by dependency on their geometries. The volumetric designs of the spinning components complicate the mathematical models of inertial torques generated by rotating bodies.²⁰ The correct mathematical modelling for the inertial torques generated by rotating masses of solid and hollow spheres is presented in this manuscript.

Centrifugal torques acting on a spinning sphere

The rotating center mass and mass elements generate several inertial forces acting on the spinning sphere. The inertial torques are acting simultaneously on the spinning sphere with a uniform circular motion.^1–5 This section considers the action of the inertial torques on the solid and hollow spheres where mass elements are distributed on the spherical surfaces. The rotation of mass elements generates the centrifugal forces acting strictly perpendicular to the axis $oz$ and $ox$ of the spinning sphere. The analytical approach for the modeling of the action of the centrifugal forces of the spinning sphere is the same as for the spinning disc represented in Chapter 3 of the gyroscope theory.¹⁹ The rotating mass elements of the sphere are located on the spherical surface of the 2/3 radius for the solid sphere and the middle radius for the hollow sphere. The analysis of the acting inertial forces generated by the mass element of the sphere is considered on the arbitrary planes that parallel to the plane of the maximal diameter of the sphere (Figure 1). The arbitrary circle plane of the sphere is the same as the plane $xoy$ of the thin disc represented in.¹⁹ The plane of the mass elements generates the change in the vector components $f_{ct.z}$ , whose directions are parallel to the spinning sphere axle $oz$ . The integrated product of components for the vector change in the centrifugal forces $f_{ct.z}$ and their variable radius of location relative to axis $ox$ and $oy$ generate the resistance torque $T_{ct,x}$ and precession torque $T_{ct,x}$ . acting about axes $ox$ and $oy$ , respectively, whose expressions are identical.¹⁹

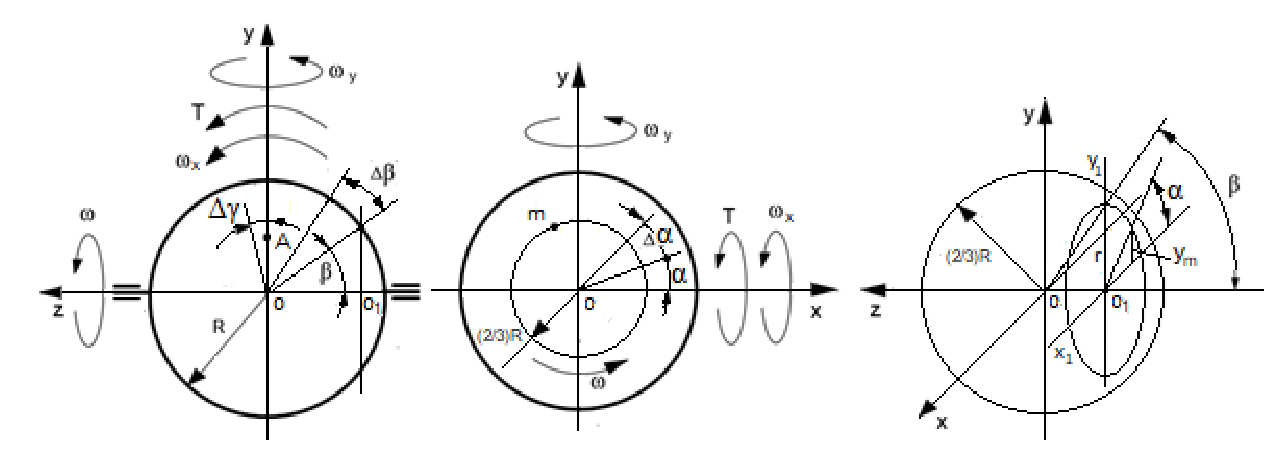
Figure 1 Schematic of the spinning sphere, its motions, and acting external torque.

The mass element m is disposed on the radius $R_i$ of the sphere, where $i$ indicates the solid $ss$ and hollow $hs$ spheres $(R_{ss}=\left(2/3\right)R$ for the solid sphere and $R_{hs}=R$ for the hollow sphere). The sphere rotates in a uniform circular motion with a constant angular velocity ω in the counter-clockwise direction and generates the plane of the centrifugal forces $f_{ct}$ acting perpendicular to axis $oz$ . The centrifugal forces $f_{ct}$ represent the distributed load where the sphere’s mass elements are located. The inclination of the spinning sphere on the minor angle Δγ generates the change in the vector’s components $f_{ct.z}$ , whose directions are parallel to the sphere axle $oz$ . The integrated product of the vector change in the centrifugal forces $f_{ct.z}$ and their variable radius r about axis $ox$ generates the resistance torque $T_{ct}$ acting opposite to the external torque T.

The resistance torque $\Delta T_{ct}$ of the centrifugal force $f_{ct.z}$ is expressed by the following:

$\Delta T_{ct.}=f_{ct.z}{y}_m$                      (1)

where y_m = R_isinβsinα is the normal component of r to axis $o_1{x}_{1,}$ other components are as specified above.

The component of the centrifugal force $f_{ct.z}$ for arbitrarily chosen plane is represented by the following equation:

$f_{ct.z}=f_{ct}sin\Delta \gamma =mr{\omega }^{2}sin\Delta \gamma$ (2)

where $f_{ct}=mr{\omega }^2$ is the centrifugal force of the mass element m;, $m=\frac{M}{4\pi R_i^2}\Delta \delta R_i^2=\frac{M}{4\pi }\Delta \delta$ , M is the mass of the sphere; $4\pi$ is the spherical angle; $\Delta \delta$ is the spherical angle of the mass element; the radius r of the mass element rotation at the plane $o_1{x}_1{y}_1$ is $r=(2/3)R_i\sin \beta$ , where

$R_{ss}=(2/3)R$ is the radius of the solid sphere;$R_{hs}=R$ is the radius of the hollow sphere; ω is the constant angular velocity of the sphere; α is the angle of the mass element’s location on the plane that parallel to plane $xoy;\beta$ is the angle of the mass element’s location on the plane $yoz;\Delta \gamma$ is the angle of turn for the sphere’s plane around axis $ox(sin\Delta \gamma =\Delta \gamma$ for the small values of the angle)

Substituting the defined parameters into Eq. (1) yields the following:

-for the solid sphere

$f_{ct.s}=-\frac{M}{4\pi }{\omega }^2\Delta \delta \Delta \gamma \frac{2}{3}R\sin \beta \sin \alpha =-\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha$ (3)

-for the hollow sphere

$f_{ct.z}=-\frac{M}{4\pi }{\omega }^2\Delta \delta \Delta \gamma \times R\sin \beta \sin \alpha =-\frac{MR{\omega }^2}{4\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha$ (4)

where all components are as specified above.

The change in the vectors of the centrifugal forces $f_{cf}$ on the angle $\Delta \gamma$ presents the vectors $f_{ct.z}$ which act around axis $ox$ in Figure 2.

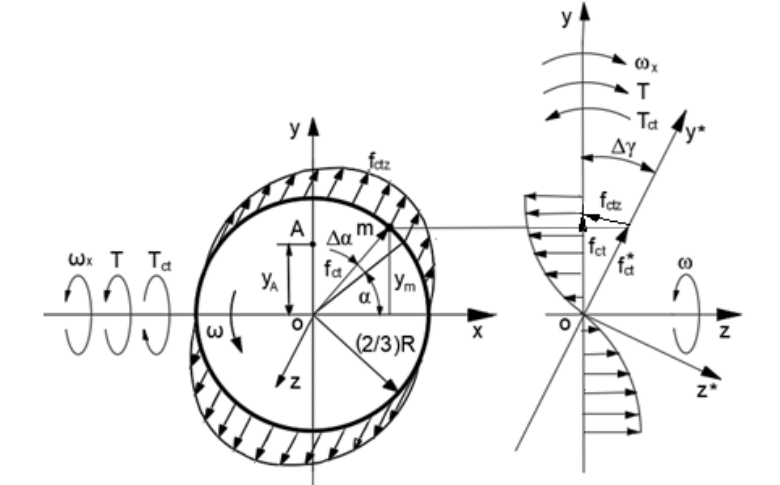
Figure 2 Schematic of acting centrifugal forces and torques on the cross-section of the sphere about the axis ox.

The resultant torque is the product of the integrated centrifugal forces $f_{ctz}$ and the centroid $y_A$ (point A, Figure 2). The centroid is defined by the following expression:^7,8

-for the solid sphere

$\begin{array}{l}{y}_A=\frac{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}{f}_{ct.z}{y}_{m}d\alpha d\beta }{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}{f}_{ct.z}d\alpha d\beta }=\frac{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha \times \frac{2}{3}R\sin \beta \sin \alpha d\alpha d\beta }{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha d\beta d\alpha }=\\ \frac{\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma \frac{2}{3}R\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}\sin \beta \sin \alpha \sin \beta \sin \alpha dd\beta }{\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma \frac{2}{3}R\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}\sin \beta \sin \alpha d\beta d\alpha }=\frac{\frac{2}{3}R\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}{\sin }^2\beta {\sin }^2\alpha d\beta d\alpha }{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}\sin \beta \sin \alpha d\beta d\alpha }\end{array}$ (5)

-for the hollow sphere

$\begin{array}{l}{y}_A=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi 2}{\int }}{f}_{ct.z}{y}_{m}d\alpha d\beta }}}{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi /2}{\int }}{f}_{ct.z}d\alpha d\beta }}}=\frac{{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi /2}{\int }}\frac{MR{\omega }^2}{4\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha \times R\sin \beta \sin \alpha d\beta d\alpha }}}{{\displaystyle \underset{\alpha =}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi /2}{\int }}\frac{MR{\omega }^2}{4\pi }\Delta \delta \Delta \gamma \sin \beta \sin \alpha d\beta d\alpha }}}=\\ \frac{\frac{MR{\omega }^2}{4\pi }\Delta \delta \Delta \gamma \times R{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi /2}{\int }}\sin \beta \sin \alpha \sin \beta \sin \alpha d\beta d\alpha }}}{\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma {\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi /2}{\int }}\sin \beta \sin \alpha d\beta d\alpha }}}=\frac{R{\displaystyle \underset{\alpha =0}{\overset{\pi }{\int }}{\displaystyle \underset{\beta =0}{\overset{\pi /2}{\int }}{\sin }^2\beta {\sin }^2\alpha d\beta d\alpha }}}{{\displaystyle \underset{\beta =0}{\overset{\pi /2}{\int }}\sin \beta d\beta }{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin \alpha d\alpha }}\end{array}$ (6)

where the components $\frac{MR{\omega }^2}{6\pi }\Delta \delta \Delta \gamma$ , $\frac{MR{\omega }^2}{4\pi }\Delta \delta \Delta \gamma$ are accepted at this stage of computing as a constant for Eqs. (5) and (6), respectively.

 Substituting defined parameters $v_m$ into Eqs. (3) and (4), where $\sin \alpha =\underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha$ $\sin \beta =\underset{0}{\overset{\pi }{\int }}\cos \beta d\beta$ , $\sin \beta =\underset{0}{\overset{\pi }{\int }}\cos \beta d\beta$ , ${\sin }^2\alpha =\frac{1}{2}\left(1-\cos 2\alpha \right)$ , ${\sin }^2\beta =\frac{1}{2}\left(1-\cos 2\beta \right)$ and represented by the integral forms: and expressed by the integral forms with the limit for the hemisphere, the following equations emerge: 

-for the solid sphere   

$\underset{0}{\overset{T_{ct}}{\int }}d{T}_{ct}=-\frac{MR{\omega }^2}{6\pi }\underset{0}{\overset{\pi }{\int }}d\delta \underset{0}{\overset{y}{\int }}d\gamma \underset{0}{\overset{\pi /2}{\int }}\cos \beta d\beta \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha \times \frac{\frac{2}{3}R\times \frac{1}{2}\underset{0}{\overset{\pi /2}{\int }}\left(1-\cos 2\beta \right)d\beta \times \frac{1}{2}\underset{0}{\overset{\pi }{\int }}\left(1-\cos 2\alpha \right)d\alpha }{\underset{\beta =0}{\overset{\pi /2}{\int }}\sin \beta d\beta \underset{0}{\overset{\pi }{\int }}\sin \alpha d\alpha }$ (7)

-for the hollow sphere

$\underset{0}{\overset{T_{ct}}{\int }}d{T}_{ct}=-\frac{MR{\omega }^2}{4\pi }\underset{0}{\overset{\pi }{\int }}d\delta \underset{0}{\overset{y}{\int }}d\gamma \underset{0}{\overset{\pi /2}{\int }}\cos \beta d\beta \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha \times \frac{\frac{1}{2}R\underset{0}{\overset{\pi /2}{\int }}\left(1-\cos 2\beta \right)d\beta \times \frac{1}{2}\underset{0}{\overset{\pi }{\int }}\left(1-\cos 2\alpha \right)d\alpha }{\underset{\beta =0}{\overset{\pi /2}{\int }}\sin \beta d\beta \underset{\beta =0}{\overset{\pi }{\int }}\sin \alpha d\alpha }$ (8)

Solving of integral Eqs. (7) and (8) yield the following:

-for the solid sphere

$\begin{array}{l}{T}_{ct}|{}_0^{T_{ct}}=-\frac{MR{\omega }^2}{6\pi }\times \left(\delta |{}_0^{\pi }\right)\times \left(\gamma |{}_0^{\gamma }\right)\times \sin \beta |{}_0^{\pi /2}\times \\ 2\sin \alpha |{}_0^{\pi /2}\times \frac{\frac{1}{6}R\left(\beta -\frac{1}{2}\sin 2\beta \right)|{}_0^{\pi /2}\times \left(\alpha -\frac{1}{2}\sin 2\alpha \right)|{}_0^{\pi }}{\left(-\cos \beta \right)|{}_0^{\pi /2}\times \left(-\cos \alpha \right)|{}_0^{\pi }}\end{array}$

that gave rise to the following

$T_{ct}=-\frac{MR{\omega }^2}{6\pi }\times \left(\pi -0\right)\times \left(\gamma -0\right)\times \left(1-0\right)\times 2\left(1-0\right)\times \frac{\frac{1}{6}\left[R\left(\frac{\pi }{2}-0\right)-0\right]\times \left[\left(\pi -0\right)-0\right]}{\left[1-\left(0-1\right)\right]\times \left[-\left(-1-1\right)\right]}=-\frac{M{R}^2{\pi }^2{\omega }^2}{72}\gamma$ (9)

-for the hollow sphere                                                                                   

$T_{ct}|{}_0^{T_{ct}}=-\frac{MR{\omega }^2}{4\pi }\times \left(\delta |{}_0^{\pi }\right)\times \left(\gamma |{}_0^{\gamma }\right)\times \sin \beta |{}_0^{\pi /2}\times 2\sin \alpha |{}_0^{\pi /2}\times \frac{R\times \frac{1}{2}\left(\beta -\frac{1}{2}\sin 2\beta \right)|{}_0^{\pi /2}\times \left(\alpha -\frac{1}{2}\sin 2\alpha \right)|{}_0^{\pi }}{\left(-\cos \beta \right)|{}_0^{\pi /2}\times \left(-\cos \alpha \right)|{}_0^{\pi }}$

that gave rise to the following

$T_{ct}=-\frac{MR{\omega }^2}{4\pi }\times \left(\pi -0\right)\times \left(\gamma -0\right)\times \left(1-0\right)\times 2\left(1-0\right)\times \frac{\frac{R}{4}\left[\left(\frac{\pi }{2}-0\right)-0\right]\times \left[\left(\pi -0\right)-0\right]}{\left[1-\left(0-1\right)\right]\times \left[-\left(-1-1\right)\right]}=-\frac{M{R}^2{\pi }^2{\omega }^2}{32}\gamma$ (10)

where the change of the limits is taken for a quarter of the sphere.

The angle γ is variable and depends on the angular velocity ${\omega }_x$ of the sphere about axis ox.

The rate of change in the torque $T_{ct}$ per time is expressed by the differential equation

-for the solid sphere                                                                                      

$\frac{d{T}_{ct}}{dt}=-\frac{M{R}^2{\pi }^2{\omega }^2}{72}\frac{d\gamma }{dt}$ (11)

-for the hollow sphere

$\frac{d{T}_{ct}}{dt}=-\frac{M{R}^2{\pi }^2{\omega }^2}{32}\frac{d\gamma }{dt}$ (12)

where $t=\alpha /\omega$ is the time taken relative to the angular velocity of the spinning sphere and other parameters are as specified above.

The differential of time and the angle is: $dt=\frac{d\alpha }{\omega }$ , the expression $\frac{d\gamma }{dt}={\omega }_x$ is the angular velocity of the sphere’s precession around axis ox. Substituting the defined components into Eqs. (11) and (12), separation of variables, presentation by the integral forms with defined limits, and solutions yield the following:

-for the solid sphere

$\frac{\omega d{T}_{ct}}{d\alpha }=-\frac{M{R}^2{\pi }^2{\omega }^2}{32}{\omega }_x$ , $d{T}_{ct}=-\frac{M{R}^2{\pi }^2\omega {\omega }_x}{72}d\alpha$ , ${\displaystyle \underset{0}{\overset{T_{ct}}{\int }}d{T}_{ct}}=-{\displaystyle \underset{0}{\overset{T_{ct}}{\int }}\frac{M{R}^2{\pi }^2\omega {\omega }_x}{72}}d\alpha$

$T_{ct}=-\frac{1}{72}M{R}^2{\pi }^2\omega {\omega }_x$ (13)

-for the hollow sphere

$\frac{\omega d{T}_{ct}}{d\alpha }=-\frac{M{R}^2{\pi }^2{\omega }^2}{32}{\omega }_x$ , $d{T}_{ct}=-\frac{M{R}^2{\pi }^2\omega {\omega }_x}{32}d\alpha$ , ${\displaystyle \underset{0}{\overset{T_{ct}}{\int }}d{T}_{ct}}=-{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{M{R}^2{\pi }^2\omega {\omega }_x}{32}}d\alpha$

$T_{ct}=-\frac{1}{32}M{R}^2{\pi }^2\omega {\omega }_x$  (14)

The torque acts on the upper and lower and left and right sides of the sphere then the total resistance torque $T_{ct}$ of Eq. (13) and (14) is increased four times

-for the solid sphere 

$T_{ct}=\pm \frac{2\times 2}{72}M{R}^2{\pi }^2\omega {\omega }_x=\pm \frac{5}{36}{\pi }^{2}J\omega {\omega }_x$ (15)

-for the hollow sphere

$T_{ct}=\pm \frac{2\times 2}{32}M{R}^2{\pi }^2\omega {\omega }_x=\pm \frac{3}{16}{\pi }^{2}J\omega {\omega }_x$ (16)        

where $J=2M{R}^2/5$ and $J=2M{R}^2/3$ is the sphere mass moment of inertia for solid and hollow spheres respectively, other parameters are as specified above. The sign (±) is (+) for the precession torque whose direction is counter-clockwise about axis oy and (-) for the resistance torque whose direction is clockwise about the axis ox.

The expression for the precession torque generated by the centrifugal forces of the mass element is the same as for the resistance torque of the sphere considered above. The precession torque of the centrifugal forces acts around the axis oy as illustrated in Figure 2.

Coriolis torque and the change in the angular momentum acting on a spinning sphere

The modeling of the action of Coriolis forces generated by the mass elements of the spinning sphere is almost the same as for the centrifugal forces.¹⁹ Coriolis forces are generated by the rotating mass elements located on parallel planes of the sphere. The resistance torque $\Delta T_{cr}$ of Coriolis force of the mass elements $f_{cr}$ of the spinning sphere is expressed by the following:

$\Delta T_{cr}=-f_{cr}{y}_m=-m{a}_z{y}_m$        (17)

where $y_m=R_{i}sin\alpha sin\beta$ is the distance to the mass element’s location along with axes oz and ox; other components are represented in Eq. (2).

The expression for $a_z$ is represented by the following:   

${\alpha }_z=-\frac{d{V}_z}{dt}=\frac{d(V\cos \alpha \sin \Delta \gamma )}{dt}=-V\cos \alpha \frac{d\gamma }{dt}=-R_i\sin \beta \cos \alpha \omega {\omega }_x$ (18)       

where $a_z=d{V}_z/dt$ is Coriolis acceleration of the mass element along with axis oz; $V_z=Vcos\alpha sin\Delta \gamma =R_i\omega cos\alpha cos\beta sin\Delta \gamma$ is the change in the tangential velocity V of the mass element; $sin\Delta \gamma =\Delta \gamma$ for the small-angle; other components are as specified above.

Substituting defined parameters into the expression of Coriolis force $f_{cr}$ (Eq. (17)) brings the following equations:

-for the solid sphere

$f_{cr}=-\frac{M\Delta \delta }{4\pi }\frac{2}{3}R\omega {\omega }_x\sin \beta \cos \alpha =\frac{MR\Delta \delta }{6\pi }\omega {\omega }_x\sin \beta \cos \alpha$ (19)

-for the hollow sphere

$f_{cr}=-\frac{M\Delta \delta }{4\pi }R\omega {\omega }_x\sin \beta \cos \alpha =\frac{MR\Delta \delta }{4\pi }\omega {\omega }_x\sin \beta \cos \alpha$ (20)

Substituting defined parameters into (Eq. 17) yields the following equations:

-for the solid sphere

$\Delta T_{cr}=\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }\sin \beta \cos \alpha \times y_m$ (21)

for the hollow sphere

$\Delta T_{cr}=\frac{MR\omega {\omega }_x\Delta \delta }{4\pi }\sin \beta \cos \alpha \times y_m$ (22)

The change in the tangential velocity V of the mass elements of the cross-section of the sphere rotating about the axis ox presents the Coriolis acceleration $a_z$  (Figure 3).

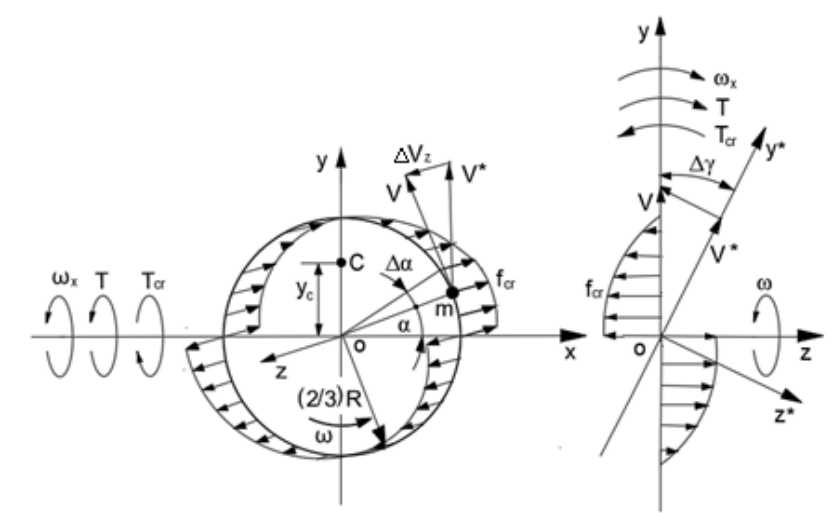
Figure 3 Schematic of the acting Coriolis forces, torques, and motions of the spinning sphere.

The location of the resultant force is the centroid of the area under the Coriolis force curve calculated by Eq. (5) for the centroid A. The centroid point C is defined for the resultant Coriolis force acting around the axis ox.

-for the solid sphere

$\begin{array}{l}{y}_c=\frac{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}{f}_{cr}{y}_{m}d\alpha d\beta }{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}{f}_{cr}d\alpha d\beta }=\frac{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}\frac{MR\omega {\omega }_x\Delta {\delta }^2}{6\pi }\sin \beta \cos \alpha \times \frac{2}{3}R\sin \alpha \sin \beta d\alpha d\beta }{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }\sin \beta \cos \alpha d\alpha d\beta }=\\ \frac{\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }\underset{\alpha =0}{\overset{\pi }{\int }}\frac{2}{3}R\sin \beta \cos \alpha d\alpha \times \underset{0}{\overset{\pi /2}{\int }}\sin \beta \cos \beta d\beta }{\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }\underset{\alpha =0}{\overset{\pi /2}{\int }}\sin \beta d\beta \times \underset{0}{\overset{\pi /2}{\int }}\cos \alpha d\alpha }=\frac{\frac{2}{3}R\underset{0}{\overset{\pi /2}{\int }}{\sin }^2\beta d\times \underset{0}{\overset{\pi }{\int }}\sin \alpha \cos \alpha d\alpha }{\underset{\alpha =0}{\overset{\pi /2}{\int }}\sin \beta d\beta \times \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }\end{array}$  (23)

-for the hollow sphere

$\begin{array}{l}{y}_c=\frac{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}{f}_{cr}{y}_{m}d\alpha d\beta }{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}{f}_{cr}d\alpha d\beta }=\frac{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}\frac{MR\omega {\omega }_x\Delta {\delta }^2}{4\pi }\sin \beta \cos \alpha \times R\sin \alpha \sin \beta d\alpha d\beta }{\underset{\alpha =0}{\overset{\pi }{\int }}\underset{\beta =0}{\overset{\pi /2}{\int }}\frac{MR\omega {\omega }_x\Delta \delta }{4\pi }\sin \beta \cos \alpha d\alpha d\beta }=\\ \frac{\frac{MR\omega {\omega }_x\Delta \delta }{4\pi }\underset{\alpha =0}{\overset{\pi }{\int }}R\sin \alpha \cos \alpha d\alpha \times \underset{0}{\overset{\pi /2}{\int }}{\sin }^2\beta d\beta }{\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }\underset{\alpha =0}{\overset{\pi /2}{\int }}\sin \beta d\beta \times \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }=\frac{R\underset{0}{\overset{\pi }{\int }}\sin \alpha d\sin \alpha \times \underset{0}{\overset{\pi /2}{\int }}{\sin }^2\beta d\beta }{\underset{0}{\overset{\pi /2}{\int }}\sin \beta d\beta \times \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }\end{array}$ (24)

where the components $\frac{MR\omega {\omega }_x\Delta \delta }{6\pi }$ and $\frac{MR\omega {\omega }_x\Delta \delta }{4\pi }$ is accepted as constant and the expression

The expressions of y_C (Eqs. (23) and (24)) are substituted into Eqs. (21) and (22) respectively where

$\cos \alpha =\underset{0}{\overset{\pi }{\int }}-\sin \alpha d\alpha$ , $\sin \beta =\underset{0}{\overset{\pi }{\int }}\cos \beta d\beta$ , ${\sin }^2\beta =\frac{1}{2}(1-\cos 2\beta )$ , and represented by the integral forms:

-for the solid sphere:                                                                                     

$\underset{0}{\overset{T_{cr}}{\int }}d{T}_{cr}=\frac{MR\omega {\omega }_x}{6\pi }\underset{0}{\overset{\pi }{\int }}d\delta \times \underset{0}{\overset{\pi /2}{\int }}\cos \beta d\beta \underset{0}{\overset{\pi }{\int }}-\sin \alpha d\alpha \times \frac{\frac{2}{3}R\underset{0}{\overset{\pi }{\int }}\sin \alpha d\sin \alpha \times \underset{0}{\overset{\pi /2}{\int }}{\sin }^2\beta d\beta }{\underset{0}{\overset{\pi /2}{\int }}{\sin }^2\beta d\beta \times \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }$ (25)

-for the hollow sphere:

$\underset{0}{\overset{T_{cr}}{\int }}d{T}_{cr}=\frac{MR\omega {\omega }_x}{4\pi }\underset{0}{\overset{\pi }{\int }}d\delta \times \underset{0}{\overset{\pi /2}{\int }}\cos \beta d\beta \underset{0}{\overset{\pi }{\int }}-\sin \alpha d\alpha \times \frac{R\underset{0}{\overset{\pi }{\int }}\sin \alpha d\sin \alpha \times \underset{0}{\overset{\pi /2}{\int }}{\sin }^2\beta d\beta }{\underset{0}{\overset{\pi /2}{\int }}\sin \beta d\beta \times \underset{0}{\overset{\pi }{\int }}\cos \alpha d\alpha }$ (26)

where the limits of integration for the trigonometric expressions are taken for the hemisphere.

Solving of integrals Eq. (25) and (26) yields the following:

- for the solid sphere

$T_{cr}|{}_0^{T_{cr}}=\frac{MR\omega {\omega }_x}{6\pi }\times \left(\delta |{}_0^{\pi }\right)\sin \beta \left(\delta |{}_0^{\pi /2}\right)\times \left(2\cos \alpha |{}_0^{\pi /2}\right)\frac{\frac{2}{3}R\times 2\frac{{\sin }^2\alpha }{2}|{}_0^{\pi /2}\times \frac{1}{2}\left(\beta -\frac{\sin 2\beta }{2}\right)|{}_0^{\pi /2}}{-\cos \beta |{}_0^{\pi /2}\times \left(\sin \beta \right)|{}_0^{\pi }}$

that gave rise to the following

$T_{cr}=\frac{MR\omega {\omega }_x}{6\pi }\times (\pi -0)\times (1-0)\times (-)(-1-1)\times \frac{\frac{2}{3}R(1-0)\times \frac{1}{2}\left(\frac{\pi }{2}-0\right)}{-(0-1)\times 2(1-0)}=-\frac{M{R}^2\pi \omega {\omega }_x}{36}$ (27)

-for the hollow sphere

$T_{cr}|{}_0^{T_{cr}}=\frac{MR\omega {\omega }_x}{4\pi }\times \left(\delta |{}_0^{\pi }\right)\times \left(\sin \beta |{}_0^{\pi /2}\right)\times \left(\cos \alpha |{}_0^{\pi }\right)\times \frac{R\times 2\frac{{\sin }^2\alpha }{2}|{}_0^{\pi /2}\times \frac{1}{2}\left(\beta -\frac{\sin 2\beta }{2}\right)|{}_0^{\pi /2}}{\left(-\cos \beta \right)|{}_0^{\pi }\times 2\sin \alpha |{}_0^{\pi /2}}$

that gave rise to the following

$T_{cr}=\frac{MR\omega {\omega }_x}{4\pi }\times (\pi -0)\times (1-0)\times (-1-1)\times \frac{R(1-0)\times \frac{1}{2}\left(\frac{\pi }{2}-0\right)}{-(0-1)\times 2(1-0)}=-\frac{1}{16}M{R}^2\pi \omega {\omega }_x$ (28)

The change of the limits at Eqs. (27) and (28) are taken for the quarter hemisphere.

Coriolis forces act on the upper and lower and left and right sides of the quarter hemisphere, and then the total resistance torque $T_{cr}$ is obtained when the result of Eqs. (27) and (28) is increased four times:

- for the solid sphere

$T_{cr}=-2\times 2\times \frac{M{R}^2\pi \omega {\omega }_x}{36}=-\frac{5}{18}\pi J\omega {\omega }_x$ (29)

-for the hollow sphere

$T_{cr}=-2\times 2\times \frac{M{R}^2\pi \omega {\omega }_x}{16}=-\frac{3}{8}\pi J\omega {\omega }_x$ (30)

where $J=2M{R}^2/5$ and $J=2M{R}^2/3$ ^7,8 is the sphere mass moment of inertia for solid and hollow spheres, respectively, other parameters are as specified above, and the sign (-) means the action of the torque in the clockwise direction.

The inertial torque of the change in the angular momentum is well-known in publications and presented by the following expression:

$T_{am}=J\omega {\omega }_x$ (31)

The analysis of Eqs. (17) and (31) show the resistance torques generated by centrifugal and Coriolis forces of the spinning sphere’s mass elements showing their summary action is opposite to the external torque. The precession torques are the sum of torques generated by the centrifugal inertial torque and the change in the angular momentum. The total resistance $T_r$ and precession torque $T_p$ have represented a sum of these torques whose equations are as follows:

$T_r=\frac{5}{36}{\pi }^{3}J\omega {\omega }_x+\frac{5}{18}\pi J\omega {\omega }_x=\frac{5}{18}\pi \left(\frac{{\pi }^2}{2}+1\right)J\omega {\omega }_x$ (32)

$T_p=\frac{5}{36}{\pi }^{3}J\omega {\omega }_x+J\omega {\omega }_x=\left(\frac{5}{36}{\pi }^3+1\right)J\omega {\omega }_x$ (33)

-for the hollow sphere

$T_r=\frac{3}{16}{\pi }^{3}J\omega {\omega }_x+\frac{3}{8}\pi J\omega {\omega }_x=\frac{3}{8}\pi \left(\frac{{\pi }^2}{2}+1\right)J\omega {\omega }_x$ (34)

$T_p=\frac{3}{16}{\pi }^{3}J\omega {\omega }_x+J\omega {\omega }_x=\left(\frac{3}{16}{\pi }^3+1\right)J\omega {\omega }_x$ (35)

where all components are as specified above

Attributes of the inertial torques acting on the spinning sphere

The obtained expressions of the inertial torques generated by the rotating mass of the solid and hollow sphere give the ability to formulate the mathematical models for its motions and compute the gyroscopic effects. The centrifugal, common inertial, and Coriolis forces of the mass element, as well as the change in the angular momentum, generate the inertial torques. These torques contain the principal components that are the change in the angular momentum and coefficients which belong to the defined type of inertial forces. The several inertial torques generated by the one rotating mass present active physical components. The total initial precession torque acting about axis oy of the spinning sphere has represented a sum of the precession torques generated by the common inertial forces of the mass elements and the change in the angular momentum. The total initial resistance torque $T_r$ acting around axis ox has represented a sum of the resistance torques generated by the centrifugal and Coriolis forces of the sphere’s mass elements. The mathematical models for internal torques acting on the spinning sphere are represented in Table 1.

The parameters of Table 1 are J is the moment of inertia of the sphere; ω is the angular velocity of the sphere; is the angular velocity of the sphere about axis ox,.The equations used to calculate the gyroscopic effects in engineering are derived from the inertial torques acting on the spinning solid and hollow sphere.

New studies of the inertial torques have shown that their values depend on the form of the spinning objects, whose geometry can be original designs. The equality of inertial torques originating along each axis defines the dependency of the angular velocities of the spinning sphere around two axes. This principle is formulated by the equality of kinetic energies of the sphere rotation about two axes ([], Chapter 4, Section 4.1.2). The relationship between the angular velocities of a spinning sphere around the oy and ox axes is defined for both solid and hollow spheres..

-The solid sphere

$\begin{array}{l}-\frac{5}{36}{\pi }^{3}J\omega {\omega }_x-\frac{5}{18}\pi J\omega {\omega }_x-\frac{5}{36}{\pi }^{3}J\omega {\omega }_y-J\omega {\omega }_y=\\ \frac{5}{36}{\pi }^{3}J\omega {\omega }_x+J\omega {\omega }_x-\frac{5}{36}{\pi }^{3}J\omega {\omega }_y-\frac{5}{18}\pi J\omega {\omega }_y\end{array}$ (36)

Simplification of Eq. (36) yields the following ratio of the angular velocities of the spinning solid sphere:

${\omega }_y=\left(\frac{5{\pi }^3+5\pi +18}{18-5\pi }\right){\omega }_x$ (37)

For the hollow sphere

$\begin{array}{l}-\frac{3}{16}{\pi }^{3}J\omega {\omega }_x-\frac{3}{8}\pi J\omega {\omega }_x-\frac{3}{16}{\pi }^{3}J\omega {\omega }_y-J\omega {\omega }_y=\\ \frac{3}{16}{\pi }^{3}J\omega {\omega }_x+J\omega {\omega }_x-\frac{3}{16}{\pi }^{3}J\omega {\omega }_y-\frac{3}{8}\pi J\omega {\omega }_y\end{array}$ (38)

Simplification of Eq. (38) yields the following ratio of the angular velocities of the spinning hollow sphere:

${\omega }_y=\left(\frac{3{\pi }^3+3\pi +8}{8-3\pi }\right){\omega }_x$ (39)

The dependency of the spinning sphere's angular velocities is used to create mathematical models for its rotation around axes ox and oy

Working example

The sphere has a mass of 1.0 kg, a radius of 0.1 m, and spinning at 3000 rpm. An external torque acts on the sphere, which rotates with an angular velocity of 0.05 rpm. It is determined the value of the resistance and precession torques acting on the spinning sphere (Figure 1). Substituting the initial data into equations of Table 1 and transformation yields the following result (Table 2).

The method for deriving the mathematical models for the inertial torques has been demonstrated on the spinning sphere. This analytical approach opens new possibilities to solve engineering problems related to the gyroscopic effect and presents the physical principles behind the acting forces. The new mathematical models for the inertial torques generated by the spinning sphere bring new knowledge to the dynamic of rotating objects of engineering mechanics.

The existing publications containing mathematical models for the inertial torques generated by the rotating mass of a spinning sphere have been found to have errors in the analytical processing of the acting forces of integral equations. There were inaccuracies in the limits of the integral equations of torques generated by the rotating mass of the sphere. The corrected mathematical models for the inertial torques of the centrifugal and Coriolis forces of the spinning sphere have been derived. These corrected inertial torques and the ratio of the angular velocities of the sphere about its axes of rotation allow for the exact solution in computing gyroscopic effects. This result presents a correct mathematical model for the inertial torques generated by the spinning sphere in the dynamics of rotating objects. The expressions of inertial torques and the ratio of the angular velocities of the sphere about its axes of rotation allow for the planning of mathematical models for its motion in space. The analytical models for the kinetically interrelated inertial torques of the spinning sphere describe the physics of its gyroscopic effects, provide a high level of accuracy in computing and open new possibilities for solving gyroscopic problems of spherical objects.

Analytical solutions for gyroscopic effects of the spinning objects of complex geometries are a sophisticated process that is linked with complex mathematical modelling of the inertial torques. In such cases, omissions in solutions and following corrections are inevitable. This statement is confirmed by the new solutions to gyroscopic effects, publications, and criticism of mistakes. The error in the expression of the limits for the integrals of the inertial torques generated by the spinning object is not fundamental but can yield distorted results in the calculation. The corrected mathematical model for the inertial torques in the aggregate with others was tested by the working example of their mathematical models for the sphere and can be used for solutions to gyroscope problems in engineering. The presented mathematical method for deriving the inertial torques acting on the spinning sphere gives the ability to solve similar problems for gyroscopic devices with curvilinear revolving components. Numerous rotating objects in engineering do not have analytical methods for computing inertial torques acting on the objects and their motions which represents a challenge to researchers and engineers.

The Kyrgyz State Technical University after I. Razzakov supported the research work for a publication that was performed as part of the employment and without financial support. The authors did not use copyediting or translation services for the preparation of the manuscript.

The authors declare that the data supporting the findings of this study are available within the article.

R. Usubamatov wrote the methodology and compiled the manuscript text, A. Arzybaev wrote the working example, and designed drawings of figures.

The authors declare that they have no conflicts of interest.

The authors declare that this research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

1. Muller D. The bizarre behavior of rotating bodies, explained. Veritasium. 2020.
2. Liang WC, Lee SC. Vorticity, gyroscopic precession, and spin-curvature force. Physical Review D. 2013;87:044024.
3. Cordeiro FJB, The gyroscope. Createspace. NV, USA. 2015.
4. Greenhill G. Report on gyroscopic theory. Relink Books, Fallbrook, CA, USA. 2015.
5. Scarborough JB. The gyroscope theory and applications. Nabu Press, London. 2014.
6. Weinberg H. Gyro mechanical Performance: the most important parameter. Analog Devices. Technical Article MS-2158. 2011;1–5.
7. Aardema MD. Analytical dynamics. Theory and application. Academic/Plenum Publishers; New York. 2005.
8. Hibbeler RC, Yap KB. Mechanics for engineers-statics and dynamics. 13th edn. Prentice-Hall: Pearson Singapore. 2013.
9. Gregory DR. Classical Mechanics. Cambridge University Press: New York. 2006.
10. Taylor JR. Classical Mechanics. University Science Books: California; USA. 2005.
11. Goldstein H, Poole C, Safko J. Classical Mechanics. 3rd edn. Addison Wesley: San Fransisco. 2017.
12. MacKay NM. Theory of physics, classical mechanics & electromagnetism, independently published. 2020.
13. Jewett J, Serway RA. Physics for scientists and engineers, cengage learning. 10th edn. USA: Boston. 2018.
14. Knight RD. Physics for scientists and engineers: a strategic approach with modern physics, Pearson, 4th edn. UK: London. 2016.
15. Nanamori Y, Takahashi M. An integrated steering law considering biased loads and singularity for control moment gyroscopes. AIAA guidance, navigation, and control conference. 2015.
16. Crassidis JL, Markley FL. Three-axis attitude estimation using rate-integrating gyroscopes. Journal of Guidance, Control, and Dynamics. 2016;39:1513–1526.
17. Sands T, Kim JJ, Agrawal BN. Nonredundant single-gimbaled control moment gyroscopes. Journal of Guidance, Control, and Dynamics. 2012;35:578–587.
18. Usubamatov R, Arzybaev A. Inertial torques acting on a spinning sphere. Int Rob Auto J. 2021;7(3):94–101.
19. Usubamatov R. Theory of gyroscopic effects for rotating objects. International Journal of Innovative Research in Science, Engineering and Technology. 2020;1(1).
20. Polyanin AD, Manzhirov AV. Handbook of mathematics for engineers and scientists. Chapman & Hall/CRC: Taylor & Francis Group. 2007.