The milk along with xanthan at levels 0, 1.9, 3.9, 5.9, 7.9, 9.9 and 0.1 and 0.2% (No 1 (control) to 11 respectively) as egg replacement were used for preparation of mayonnaise. Creaming index, heat stability, physical stability and rheological properties of samples over a were investigated. Also flow behavior of samples were fitted to Power law, Herschel-Bulkley and Casson models. It was found that addition milk along with xanthan to mayonnaise protected from phase separation in comparison to control sample. All the samples had stability higher than 99% except samples 1, 4, 5 and 6. The highest stability was recorded for sample No 11 (99.98%) and the lowest for 5(74.95%) that compared with control sample had significant differences (p>0.05). All the samples except No 1 and 5 showed heat stability higher than 99 % and the highest stability recorded for No 11(99.72%) and the lowest for No 5(67.42 %) and in comparison with control were significantly different (p> 0.05). Apparent viscosity decreased with increase the egg replacement from 40% to 80%, as the highest and lowest viscosity observed in samples contain 100% and 80% replacement respectively. All samples showed shear-thinning behavior and the high coefficients of determination for Power law and Herschel-Bulkley models (0.99) revealed the adequacy of these rheological models to describe flow behavior of mayonnaise.

Keywords: mayonnaise, xanthan, milk, shear thining, power law

Mayonnaise is a typical oil in water emulsion prepared from vegetable oil, egg yolk, vinegar, sugar, salt, mustard and a variety of food additives.¹ Among its ingredients, egg is most critical in term of stability of the mayonnaise. Egg is considered a high profile ingredient because of its high nutritional value and multifunctional properties, including emulsification, coagulation, foaming, and flavor product.² Cholesterol is present in the egg yolk in quantities varying from 180 to 250 mg, depending on hen genotype.³ The desire to replace egg in food systems was brought about by a multitude of concerns from consumers, and processors desired to have low cholesterol and safe foods.⁴ So there have been done several studies on removing or decreasing egg in mayonnaise.⁵

The oil droplets in Mayonnaise usually stabilized by protein molecules that, either alone or together with other surface-active components (such as polysaccharides), form strong and cohesive interfacial films that may resist tensile or shearing stresses and protect the oil droplets from coalescence.⁶ Several studies have been reported on the role of proteins in the stabilization of emulsions.^7,8 Emulsifiers act generally by one or more mechanisms, including reduction of the interfacial tension between oil and water phases, or covering fat globules with a charged layer to create a physical barrier preventing flocculation.⁹ Stabilizers, mainly polysaccharides, usually stabilize emulsions by increasing the viscosity of the aqueous phase. Milk whey proteins (MWP) are known to alter their adsorption behaviour at fluid interfaces responding to both different aqueous environmental conditions¹⁰ and the presence of several food additives such as lipids and polysaccharides,¹¹ sugars,¹² electrolytes,¹³ polypeptides.¹⁴ Macromolecular interactions between milk whey protein and Xanthan both in solution and at the interface vicinity depended on the protein type and on the biopolymer relative concentration in aqueous subphase.¹⁵ The main interaction mechanism that would govern milk whey protein adsorption behaviour in MWP/XG mixed systems could be biopolymer interfacial segregation between the MWP and XG in the vicinity of the air–water interface.¹⁶ Polysaccharide-protein complexes are not only employed to stabilize simple oil-in-water emulsions but can be employed in more complex systems. The possible interactions between emulsion droplets and the other components of a food can be very complex. Several ingredients are generally present and give rise to final structures which are dependent on the overall composition, on the manner in which the ingredients are added and on the time/temperature variations to which they are submitted during manufacture. It is clear that the level of knowledge about such structures is still insufficient mainly because of the complexity of the interactions, reactions and products. The role of milk proteins in the unfrozen aqueous phase is recognized but is less well studied than their role at the fat interface. Proteins interact with water and polysaccharides and their hydration is responsible for a variety of functional properties, including rheological behaviour.^17,18

Rheological properties of foods have an important role on the perception of taste or flavor. Smoothness, graininess, and viscosity can all influence perception. Extensive rheological studies have been carried out on mayonnaise, more so than on other salad dressings, because it is a more stable emulsion and it exhibits more complex viscoelastic rheological behavior¹⁹ and also Some research was carried out on the rheological properties of emulsions stabilized with low-in-cholesterol egg products, but contradictory results were obtained.^20,21

In order to prepare low cholesterol mayonnaise, application of protein, such as whey protein isolate along with some thickeners has been reported. However, there is no published data on application of whole milk along with xanthan gum (XG) to replace egg yolk (EY) in mayonnaise formulation. Therefore, the present study was conducted to prepare mayonnaise by application a desirable combination of whole milk, XG, and lowering or removing (partially, totally) egg, with comparable properties those of the conventional mayonnaise, and investigating the rheological and physical properties of the product.

Mayonnaise Preparation

Two egg replacers (xanthan gum and pasteurized, homogenized low fat milk mixture) were used in this study. According to the previous work, substitution of egg with milk and xanthan mixtures carried out and best formulation selected and done in this study. Substitution of egg with milk and xanthan mixtures from level of 0- 100% and 0-0.2% was selected respectively.²² Reduced egg mayonnaise samples (11 samples) were prepared according to the following procedure and by using ingredients written in Table 1. To prepare different mayonnaises, first powder ingredients (salt, sugar, xanthan, mustard, carboxymethyl cellulose, sorbate, benzoate) were mixed, vegetable oil was added slowly and for 5 min mixed. Vinegar gently was poured and mixed and the rest of oil was added slowly into the aqueous phase.²² Then this pre emulsion was homogenized with the stirrer operating. To compare different properties, 1 control samples (one industrial sample) were also prepared with the formulations shown in Table 1. Each formulation was prepared one time and each experiment was performed in 2 replicates. After preparation, the samples kept in refrigerator (4-5 ºC) until the analysis⁴ (Table 1).

Physical properties of Mayonnaise samples

Creaming index: Immediately after preparation, 50 mL of each emulsion was poured into a cylindrical glass tube, sealed with a plastic cap and stored at 4 °C for 30 days. The emulsion index was measured by the change in height of the bottom serum phase (H) along storage time. The creaming index (CI) was determined according to Eq. (1).²²

$CL=\left(H/H_0\right)\times 100$

where H₀ represents the initial height of the emulsion.

Physical Stability: Physical Stability of Emulsion was determined in terms of amount of oil separated from an emulsion during centrifugation. 15 gr Samples of mayonnaise (F1) were centrifuged in 15-mL tubes at 5000 rpm for 30 min at room temperature to remove the top oil layer.²³ The weight of precipitated fraction (F2) was measured, and the emulsion stability of mayonnaise was expressed as:

$Physicalstability\%\left(F2/F1\right)\times 100$

Heat stability: For measurement heat stability, 15 gr of each sample transferred to test tubes and stored at 50 °C for 48 h. They were, then, centrifuged for 10 min at 3,000 rpm. Finally, heat stability was characterized according the below equation.²³ F2 equal to the weight of precipitated fraction and F1, initial weight of sample.

$Heatstability\%\left(F2/F1\right)\times 100$

Rheological properties: The Apparent viscosity of the Mayonnaise samples determined at room temperature at Shear rate (60 s⁻¹)²⁴ with the aid of a Brookfield RDVD-II, viscometer (Brookfield Engineering Laboratories, USA) using spindle No 7 at different rpms ( 5, 10, 15, 20, 30, 40, 50, 60, 70, 80, 90, 100, 105,120,140, 150, 160, 180, 200). For each sample two readings were taken and their means were reported. 500 ml sample was placed in a 600 mL low form Griffin beaker and a disc was inserted into the sample. To eliminate any time-dependent behavior, sample was subjected to pre-shearing until a constant torque was observed. Formal data collection of torque at various rotational speeds followed immediately.²⁵ Mitschka method²⁶ tested with spindle No 7. Values of $a_i$  (on the torque dial from units 0 -100) are converted to the (average) Shear stresses ${\tau }_i$  (in pa) on spindle used by

${\tau }_i=k_{at} a_I$

Pairs of ${\tau }_i$ - $N_i$  (rotational speed in rpm) valid for spindle are plotted in the log - log form. When this dependence is sufficiently close to a linear one, the fluid under test is of the power-law type. The slope of the log τ i - log N dependence in this case is equal to the flow index of the fluid or n.

Using values of $k_{ny}$  (n) for this flow index and spindle number, the corresponding values of the Shear rates $y_i$  (in s -1) are then calculated as

$y_i=k_{ny}\left(n\right)N_i$

The relevant pairs ${\tau }_i$ - $y_i$ are assumed to be the points of the viscosity function of the fluid sample tested. Conversion factor for the method described by Mitschka²⁶ were used in this study.To determine flow parameters, flow behavior of all samples were fitted to Power law (eq. 1), Herschel- Bulkley (eq. 2), Casson (eq. 3) models, respectively.²⁷

$\tau =k{k}_y{}^{(n)}$ (eq. 1)

Where τ (Pa) is shear stress, k (Pa.sⁿ) is consistency coefficient, γ (1/s) is shear rate and n (-) is flow behavior index.

$\tau ={\tau }_0+ k\gamma$  (eq. 2)

Where τ (Pa) is shear stress, ${\tau }_0$  (Pa) is yield stress, k (Pa.sn) is consistency coefficient, γ (1/s) is shear rate and n (-) is flow behavior index.

${\tau }^{0.5}= {\tau }_0{}^{0.5}+k{\gamma }^{0.5}$ (eq. 3)

Where τ (Pa) is shear stress, τ0 (Pa) is yield stress, k (Pa^0.5.S^0.5) is consistency coefficient and γ (1/s) is shear rate.

Statistical analysis: The results in this study were evaluated by the completely randomised design using the software SPSS 16. The significant differences (P< 0.05) between the treatments were evaluated by the Duncan multiple range test procedure. All experimental determinations were assayed in triplicate.

Physical properties

Creaming index: The compositional analysis of milk and Mayonnaise, pH and acidity of samples reported in previous study.²⁸ In this study, addition of milk along with xanthan (as egg replacement) to mayonnaise protected from phase separation of the emulsions compared with control sample during storage period of 30 days. This is due to the sharp increase in viscosity which prevented the fluid from moving there by decreased creaming rate.²⁹ But the creaming phenomenon was observed in sample contains 80% replacer after 30 d period storage due to large particle size and low viscosity.³⁰ Similar creaming behaviours of different concentrations of XG in mayonnaise were explained by Sun et al.³¹ Also Hennoc et al.³² reported that in emulsions contain 60% oil, the presence of xanthan for preventing the phase separation is essential.

Physical stability: Results of physical stability shown in Figure 1. During 90 d storage period, all the samples had stability higher than 99% except samples 1, 4, 5 and 6. The highest stability was recorded for sample No 11 (99.98%) and the lowest for 5 (74.95%) that compared with control sample had significant differences (p> 0.05). during 30, 60 and 90 d storage, stability of samples No 1, 4, 5 and 6 gradually decreased and in comparison to control sample had significant differences (p> 0.05), but samples No 2, 3, 7, 8 ,9, 10 and 11 during 90 days storage showed stability higher than 99% and had not significant difference each other (p< 0.05) but compared with control sample significantly different (p>0.05). It might be due to the increased viscosity and lower particle size of these samples in comparison to others that led to slow down the droplet movement.³³ The results of this study is agree with those reported by Abu Ghoush et al.³⁴ Nikzade et al.²² and Mun et al.²³

Heat stability: In this study, all the samples except samples No 1 and 5 showed heat stability higher than 99 % during 30 d storage period. The highest stability recorded for sample No 11 ( 99.72%) and the lowest for No 5 (67.42 %) and in comparison with control were significantly different (p> 0.05), but after 60 and 6 d storage, decrease the heat stability observed in samples No 1, 5, 4 and 6, that significantly different (p> 0.05) compared with control sample. Rest of sample during 90 d storage had heat stability higher than 99% and had not significant differences compared with each other (p< 0.05). Our results were agree with those reported by Thompson & Reniers³⁵ about application of whey protein as egg replacement in salad dressing. Results shown in Figure 2 & Table 2.

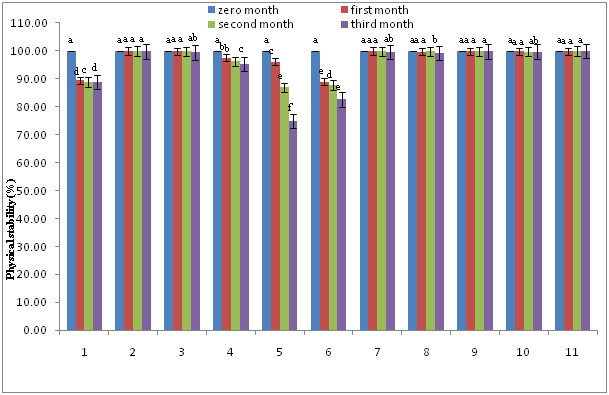
Figure 1 Changes in Physical stability, means in the same column indicated by similar letters were not significantly different (P>0.05). 1 = control sample.

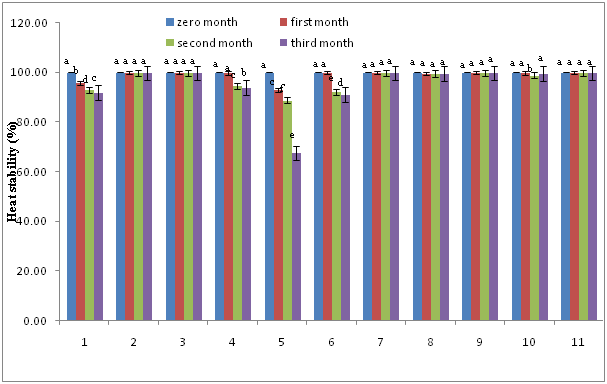
Figure 2 Changes in heat stability, means in the same column indicated by similar letters were not significantly different (P>0.05). 1 = control sample.

Rheological properties: After calculating the Shear rate, Shear stress and Apparent viscosity, established the related curves. The Apparent viscosity of mayonaise samples decreased with increase shear rate, indicating a non-Newtonian fluid and showed shear-thinning behavior that characterized by flow behavior index values of less than 1 (Table 3). In the other study, all investigated mayonnaise samples containing lupin protein and xanthan gum, showed a shear thinning behavior.³⁶

In this study, Apparent viscosity of mayonnaise samples decreased with increasing the egg replacement from 40% to 80%, as the highest and lowest viscosity observed in samples contain 100% and 80% replacement respectively (Figure 3). Increase the shear rate and replacers percentage caused to decrease the apparent viscosity, but apparent viscosity of samples contain 20%, 40% and 100% egg replacement in compared with control were higher, also with increase the xanthan, viscosity of all samples increased in comparison to control, but increase the replacers caused to decrease the viscosity of all samples except 100% replacement as the highest viscosity recorded for sample No (100% milk and 0.2 % xanthan gum). Flow rheogram of mayonnaise samples formulated by various amounts of milk, xanthan, and egg is presented in Figure 4. For all mayonnaise samples, relationship of shear stress and shear rate was nonlinear and they showed a shear thinning behavior (pseudo plastic fluids). In concentrated emulsions, the droplets are close enough together to interact with each other which may lead to the formation of a three-dimensional network of aggregated droplets and consequently to a higher viscosity. As the shear rate is increased, the hydrodynamic forces cause aggregates to become deformed and eventually disrupted which results in a reduction in the viscosity.^37,38

Due to the commercial importance of mayonnaise, the rheological characteristics of mayonnaise have been extensively studied. The flow properties (consistency index, K; flow behavior index, n; and yield stress, to) of mayonnaise have been studied by Paredes et al.³⁹ Yilmazer et al.⁴⁰ and Several rheological equations, such as the power law, the Casson model, and the Herschel-Bulkley model, have been used to describe the stress response to deformation in mayonnaise.³⁹ However, the reported flow parameters (K, n, and yield stress) are different from reference to reference due to differences in selected measuring ranges, corrections considered, and types of products.

In this study, the flow parameters obtained by fitting the data to Power law, Herschel-Bulkley and Casson models. High coefficients of determination for Power law and Herschel-Bulkley models (0.99) revealed the adequacy of these rheological models to describe flow behavior of mayonnaise samples. This is agree with those reported by Maruyama et al.⁴¹ Liu et al.⁴ Mun et al.²³ and Su et al.³¹ about mayonnaise.

Figure 3 Apparent viscosity versus Shear rate for different mayonnaise samples.

Figure 4 Shear stress versus Shear rate for different mayonnaise samples.

Power law parameters for samples: Consistency index, K, of samples with increase the replacing percentage up to 40% increased, but for upper contents except 100% replacing, decreased, as the highest Consistency index, K (100.82 pa.s) observed in sample contains 100% milk along with 0.2% xanthan, and the lowest (28.99 pa.s) recorded for sample contains 80% replacement along with 0.1% xanthan. These results were not similar with those reported by Rahmati et al.⁴² about soya milk as egg replacement in mayonnaise. Also the highest shear thickening property observed for control and 100% milk replacement along with 0.2% xanthan. Also for all samples, flow behavior index, n, recorded less than 1, and showed shear-thinning behavior.

Herschel-Bulkley parameters for samples: The lightest yield stress observed in samples contain 20% replacement (54.68 and 31.15 pa) and then 100% replacement (48.91 and 38.03 pa). Consistency index, K, of samples with increase the replacing percentage up to 40% increased, but for upper contents except 100% replacement, decreased, as the highest Consistency index, K (69.30 pa.s) observed in sample contains 100% milk along with 0.2% xanthan, and the lowest (12.63 pa.s) recorded for sample contains 80% replacement along with 0.1% xanthan. Results of this study were not similar with those reported by Rahmati et al.⁴² about soya milk as egg replacement in mayonnaise (increase the soya milk in mayonnaise caused decrease the K)

Casson parameters for samples: This model had low Coordination for characterize the rheological behavior of mayonnaise in comparison to two previous model. As a result, in spite of high R2 (0.95-0.98), Casson model was found to be an inappropriate rheological model. In the other study, all investigated mayonnaise samples containing lupin protein and xanthan gum, showed a shear thinning behavior.³⁶ The Power law model and Herschel-Bulkley were able to properly explain flow characteristics of mayonnaise samples. From this point of view, it can be concluded that milk with xanthan gum, not only maintained the structure of mayonnaise, but had a greater effect on the viscosity and flow parameters of mayonnaise samples compared to egg.

It was found that Flow behavior index values of different mayonnaise samples were determined less than 1, which indicates the samples are shear thining. Rheological characteristics of all samples were shear thinning and the apparent viscosity of them decreased with increasing shear rate. The flow parameters fitted to Power law, Herschel-Bulkley and Casson models showed that High coefficients of determination recieved for Power law and Herschel-Bulkley models (0.99), and revealed the adequacy of these rheological models to describe flow behavior of mayonnaise samples.

The authors wish to thank engineer Barat Ali Zarei Yam and eng Ehsan Akbari for critical helps and valuable suggestions.

The author declares no conflict of interest.

1. Juszczak L, Fortuna T, Kośla A. Sensory and rheological properties of polish commercial mayonnaise. Die Nahrung. 2003;47(4):232–235.
2. Narsimhan G, Wang Z. Guidelines for processing emulsion-based foods. In: Hasenhuettl GL, et al. editors. Food emulsifiers and their applications. New York, USA: Springer Sci Business Media; 2008. p. 349–389.
3. Stadelman WJ, Cotterill OJ. Egg science and technology. 3rd ed. Wesport: UK: AVI Publischer Company; 1995.
4. Liu H, Xu XM, Guo ShD. Rheological, texture and sensory properties of low fat mayonnaise with different fat mimetics. Journal of Food Science and Technology. 2007;40(6):946–954.
5. Takeda K, Matsumura Y, Shimizu M. Emulsifying and surface properties of wheat gluten under acidic conditions. J Food Sci. 2001;66(3):393–399.
6. Dickinson E, Stainsby G. Colloids in Foods. New York, USA: Applied Science; 1982.
7. Joly M. Surface and Colloid Science. New York, USA: Plenum Press; 1982. 472 p.
8. Srivastava SN, Haydon DA. Chemistry, Physics and AEElications of Surface Active Substances." In: Overbeek JThG editor. London, UK: Academic Press; 1967. 122 p.
9. Walstra P. Overview of emulsion and foam stability. In: Dickinson E editor. Food Emulsion and Foams. London, UK: The Royal Society of Chemistry; 1986. p. 242–257.
10. Davis JP, Foegeding EA, Hansen FK. Electrostatic effects on the yield stress of whey protein isolate foams. Colloids Surfaces B: Biointerfaces. 2004;34(1):13–23.
11. Rodriguez Patino JM, Rodriguez Nino MR, Carrera C. Physico-chemical properties of surfactant and protein films. Curr Opin Colloid Interface Sci. 2007;12(4-5):187–195.
12. Yang X, Berry TK, Foegeding EA. Foams prepared from whey protein isolate and egg white protein: 1. Physical, microstructural and interfacial properties. J Food Sci. 2009;74(5):E259–268.
13. Marinova KG, Basheva ES, Nenova B, et al. Physico-chemical factors controlling the foamability and foam stability of milk proteins: sodium caseinate and whey protein concentrates. Food Hydrocolloids. 2009;23(7):1864–1878.
14. Martinez MJ, Sánchez CC, Patino JM, et al. Interactions in the aqueous phase and adsorption at the air-water interface of caseinoglycomacropeptide (GMP) and beta-lactoglobulin mixed systems. Colloids Surf B Biointerfaces. 2009;68(1):39–47.
15.  Perez AA, Carrara CR, Carrera C, et al. Interfacial dynamic properties of whey protein concentrate/polysaccharide mixtures at neutral pH. Food Hydrocolloids. 2009;23(5):1253–1262.
16. Perez AA, Sanchez CC, Rodriguez Patino JM, et al. Milk whey proteins and xanthan gum interactions in solution and at the air-water interface: A rheokinetic study. Colloids and Surfaces B: Biointerfaces. 2010;81(1):50–57.
17. Goff HD. Formation and stabilization of structure in ice cream and related products. Current Opinion Colloid Interface Sci. 2002;7(5-6):432–437.
18. Goff HD. Ice cream. In: Fox PF, et al. Advanced Dairy Chemistry - 1. Proteins, 3rd ed. New York, USA: Kluwer Academic; 2002.
19. Rao MA. Rheological behavior of processed fluid and semisolid foods. In: MA Rao editor. Rheology of Fluid and Semisolid Foods. Gaithersburg, USA: Aspen Publishers; 1999. p. 219–254.
20. Paraskevopoulou A, Kiosseoglou V, Alevisopoulos S, et al. Influence of reduced-cholesterol yolk on the viscoelastic behaviour of concentrated O/W emulsions. Colloids Surf. 1999;12(3-6):107–111.
21. Guerrero A, Ball HR. Effect of spray-dried or reduced- cholesterol yolk and temperature on the linear viscoelastic properties of mayonnaise. J Texture Stud. 1994;25(4):363–381.
22. Nikzade V, Mazaheri Tehrani M, Saadatmand-Tarzjan M. Optimization of low-cholesterol-low–fat mayonnaise formulation: Effect of using soy milk and some stabilizer by a mixture design approach. Food Hydrocolloids. 2012;28(2):344–352.
23. Mun S, Kim YL, Kang CG, et al. Development of reduced-fat mayonnaise using 4[alpha] GTase-modified rice starch and xanthan gum. Int J Biol Macromol. 2009;44(5):400–407.
24. Mohammadzadeh H, Koocheki A, Kadkhodaee R, et al. Physical and flow properties of d-limonene-in-water emulsions stabilized with whey protein concentrate and wild sage seed gum. Food Research International. 2013;53(1):312-318.
25. Steffe FJ. Bioprocessing Pipelines: Rheology and Analyses. USA: Freeman Press; 2006. 159 p.
26. Mitschka p. Simple conversion of Brookfeild RVT readings into viscosity functions. Rheologica Acta. 1982;21(2):207–209.
27. Rezaei R, Khomeiri M, Kashaninejad M, et al. Effects of guar gum and arabic gum on the physicochemical, sensory and flow behavior characteristics of frozen yoghurt. International Journal of Dairy Technology. 2011;64(4):563–568.
28. Ghajari shamooshaki M, Sadeghi Mahoonak A, Maghsoodloo Y, et al. Effect of milk and Xanthan as egg replacement on the chemical and microbial safety properties of Mayonnaise. Scholarly Journal of Agricultural Science. 2015;5(8):256–261.
29. McClements DJ. Food emulsions: principles, practices, and techniques. USA: CRC press; 2004. 634 p.
30. Mangino ME. Protein interactions in emulsions: protein-lipid interactions. In: Hettiarachchy NS, t al. editors. Protein functionality in food systems. New York, USA: M Dekker; 1994. p. 147–180.
31. Sun C, Gunasekaran S, Richards MP. Effect of xanthan gum on physicochemical properties of whey protein isolate stabilized oil-in-water emulsions. Food Hydrocolloids. 2007;21(4):555–564.
32. Hennoc M, Rahalkar RR, Richmond P. Effect of xanthan gum upon the rheology and stability of oil in water emulsions. Journal of Food Science. 1984;49(5):1271–1274.
33. Sathivel S, Bechtel P, Babbitt J, et al. Functional, nutritional, and rheological properties of protein powders from Arrow tooth Flounder and their application in mayonnaise. Journal of Food Engineering and Physical Properties. 2005;70(2):57–63.
34. Abu Ghoush M, Samhouri M, Al-Holy M, et al. Formulation and fuzzy modeling of emulsion stability and viscosity of a gum-protein emulsifier in a model mayonnaise system. Journal of Food Engineering. 2008;84(2):348–357.
35. Thompson LU, Reniers DJ. Succinylated cheese whey protein concentrates in coffee whitener and salad dressing. Journal of Dairy Science. 1981;65(7):1135–1140.
36. Raymundoa A, Francob JM, Empisc J, et al. Optimization of the composition of cow-fat oil-in-water emulsions stabilized by white lupin protein. JAOCS. 2002;79(8).
37. McClements DJ. Food emulsions; principles, practice, and techniques. Boca Raton, FL: USA: CRC Press; 1999.
38. Su HP, Lien CP, Lee TA, et al. Development of low fat mayonnaise containing polysaccharide gum as functional ingredients. J Sci Food Agric. 2010;90(5):806–812.
39. Paredes MDC, Rao MA, Bourne MC. Rheological characterization of salad dressings, 1. Steady shear, thixotropy and effect of temperature. J Texture Studies. 1998;19(3):247–258.
40. Yilmazer G, Carrillo AL, Kokini JL. Effect of propylene glycol alginate and xanthan gum on stability of O/W emulsions. J Food Sci. 1991;56(2):513–517.
41. Maruyama K, Sakashita T, Hagura Y.et al. Relationship between rheology, particle size and texture of mayonnaise. Food Science and Technology Research. 2007;13(1):1–6.
42. Rahmati K, Mazaheri Tehrani M, et al. Soy milk as an emulsifier in mayonnaise: physico-chemical, stability and sensory evaluation. Journal of Food Science and Technology. 2012;51(11):3341–3347.