In the work the structural model and the structural scheme of a piezoengine are calculated for aeronautics and aerospace. The matrix equation of a piezoactuator is determined. The mechanical characteristic and the parameters of the PZT piezoactuator are obtained in control systems for aeronautics and aerospace. A piezoengine is used for nanoalignment and nanopositioning, compensation of temperature and gravitational deformations in aeronautics and aerospace, nanoresearh for tunel microscopy, adaptive optics, astronomy for compound telescope and satellite telescope. The linear change in the size of a piezoengine occurs by the electric field changes. A piezoengine is a piezomechanical device for converting electrical energy into mechanical energy and for actuating mechanisms, systems or its controlling by using inverse piezoeeffect. Piezoceramics include barium titanate or ferroelectric ceramics, based on lead zirconate titanate type PZT, are widely used for the production of piezoengines. The PZT piezoengine is characterized by high accuracy, small overall dimensions, simple design and control, reliability and cost effectiveness. The structural general model, the scheme and the functions a piezoengine are obtained for aeronautics and aerospace. Method of applied mathematical physics is applied for determinations the characteristics of a piezoengine with using the piezoelasticity equation and the differential equation. The static and dynamic characteristics of the PZT piezoengine are determined.

Keywords: piezoengine, structural model and scheme

A piezoengine is used for aeronautics and aerospace.^1–19 This piezoengine is applied in adaptive optics system for compound telescope and satellite telescope, astrophysics, deformable mirrors, interferometers, damping vibration, scanning microscopy.^14–59 The structural model and scheme of a piezoengine are constructed.

For the structural model a piezoengine is used method of mathematical physics with the solution the piezoelasticity equationfor reverse piezoeffect and differential equation at the voltage control.^8–41

$S_i=d_{mi}{E}_m+s_{ij}^E{T}_j$

and at current the control

$S_i=g_{mi}{D}_m+s_{ij}^D{T}_j$

here $S_i$ ,$E_m$ ,$d_{mi}$ ,$T_j$ ,$d_{mi}$ ,$g_{mi}$ ,$s_{ij}^E$  are the relative displacement, the electric field strength, the electric induction, the mechanical field strength, its modules, the elastic compliance, the indexes i, j, m. The ordinary differential equation a piezoengine ^8–41 has form

$\frac{d^2\Xi \left(x,s\right)}{d{x}^2}-{\gamma }^2\Xi \left(x,s\right)=0$

here $\Xi \left(x,s\right)$ ,$x$ ,s MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqkY=grVeeu0dXdh9vqqj=hEeeu0xXdbba9frFj0=OqFf ea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaape Gaam4Caaaa@3774@ ,$\gamma$  are the transform of the displacement, its coordinate  and parameter, the propagation coefficient and the general length $l=\{l,\delta ,b$ an engine. For the transverse engine for,$x=0$ $\Xi \left(0,s\right)={\Xi }_1\left(s\right)$ ;and $x=h$ ,$\Xi \left(h,s\right)={\Xi }_2\left(s\right)$ .

Its transverse solution is written

$\Xi \left(x,s\right)=\left\{{\Xi }_1\left(s\right)sh\left[\left(h-x\right)\gamma \right]+{\Xi }_2\left(s\right)sh\left(x\gamma \right)\right\}/sh\left(h\gamma \right)$

here ${\Xi }_1\left(s\right)$ , ${\Xi }_2\left(s\right)$ ;are the transforms its end displacements.

The system equations of the boundary conditions for the transverse piezoengine is determined

$T_1\left(0,s\right)=\frac{1}{s_{11}^E}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=0}-\frac{d_{31}}{s_{11}^E}{E}_3\left(s\right)$

$T_1\left(h,s\right)=\frac{1}{s_{11}^E}{\frac{\text{d}\Xi \left(x,s\right)}{\text{d}x}|}_{x=h}-\frac{d_{31}}{s_{11}^E}{E}_3\left(s\right)$

From the reverse piezoeffect of a piezoengine at the voltage control the Laplace transform of the force causes displacement is determined

$F\left(s\right)=\frac{d_{mi}{S}_0{E}_m\left(s\right)}{s_{ij}^E}$

here$S_0$ is cross sectional area.

The transform of the force causes displacement for the transverse piezoengine at the voltage control is written

$F\left(s\right)=\frac{d_{31}{S}_0{E}_3\left(s\right)}{s_{11}^E}$

Then the reverse coefficient at the voltage control with $U\left(s\right)=E_m\left(s\right)\delta$ is determined in the form

$k_r=\frac{F\left(s\right)}{U\left(s\right)}=\frac{d_{mi}{S}_0}{\delta s_{ij}^E}$

The transverse reverse coefficient at the voltage control is obtained

$k_r=\frac{F\left(s\right)}{U\left(s\right)}=\frac{d_{31}{S}_0}{\delta s_{11}^E}$

Its transverse model is determined

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_1\left(s\right)+{\left({\chi }_{11}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{31}{E}_3\left(s\right)-\left[\gamma /sh\left(h\gamma \right)\right]\\ \times \left[ch\left(h\gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_2\left(s\right)+{\left({\chi }_{11}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{31}{E}_3\left(s\right)-\left[\gamma /\text{sh}\left(h\gamma \right)\right]\\ \times \left[\text{ch}\left(h\gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\chi }_{11}^E=s_{11}^E/S_0$

For the longitudinal piezoengine its longitudinal solution of the differential equation is written

$\Xi \left(x,s\right)=\left\{{\Xi }_1\left(s\right)sh\left[\left(\delta -x\right)\gamma \right]+{\Xi }_2\left(s\right)sh\left(x\gamma \right)\right\}/sh\left(\delta \gamma \right)$

The system of the boundary conditions for the longitudinal piezoengine is obtained

$T_3\left(0,s\right)=\frac{1}{s_{33}^E}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=0}-\frac{d_{33}}{s_{33}^E}{E}_3\left(s\right)$

$T_3\left(\delta ,s\right)=\frac{1}{s_{33}^E}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=\delta }-\frac{d_{33}}{s_{33}^E}{E}_3\left(s\right)$

The transform of the force causes displacement for the longitudinal piezo engine at the voltage control is written

$F\left(s\right)=\frac{d_{33}{S}_0{E}_3\left(s\right)}{s_{33}^E}$

The longitudinal reverse coefficient at the voltage control is obtained

$k_r=\frac{F\left(s\right)}{U\left(s\right)}=\frac{d_{33}{S}_0}{\delta s_{33}^E}$

Its longitudinal structural model is determined

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_1\left(s\right)+{\left({\chi }_{33}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{33}{E}_3\left(s\right)-\left[\gamma /\text{sh}\left(\delta \gamma \right)\right]\\ \times \left[\text{ch}\left(\delta \gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_2\left(s\right)+{\left({\chi }_{33}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{33}{E}_3\left(s\right)-\left[\gamma /\text{sh}\left(\delta \gamma \right)\right]\\ \times \left[\text{ch}\left(\delta \gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\chi }_{33}^E=s_{33}^E/S_0$

From the differential equation of for the shift piezoengine its shift solution is written

$\Xi \left(x,s\right)=\left\{{\Xi }_1\left(s\right)sh\left[\left(b-x\right)\gamma \right]+{\Xi }_2\left(s\right)sh\left(x\gamma \right)\right\}/sh\left(b\gamma \right)$

The system of the boundary conditions for the shift piezoengine is obtained

$T_5\left(0,s\right)=\frac{1}{s_{55}^E}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=0}-\frac{d_{15}}{s_{55}^E}{E}_1\left(s\right)$

$T_5\left(b,s\right)=\frac{1}{s_{55}^E}{\frac{\text{d}\Xi \left(x,s\right)}{\text{d}x}|}_{x=b}-\frac{d_{15}}{s_{55}^E}{E}_1\left(s\right)$

The transform of the force causes displacement for the shift piezo engine at the voltage control is written

$F\left(s\right)=\frac{d_{15}{S}_0{E}_3\left(s\right)}{s_{55}^E}$

The shif reverse coefficient at the voltage control is obtained

$k_r=\frac{F\left(s\right)}{U\left(s\right)}=\frac{d_{15}{S}_0}{\delta s_{55}^E}$

Its structural shift model is determined

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_1\left(s\right)+{\left({\chi }_{55}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{15}{E}_1\left(s\right)-\left[\gamma /sh\left(b\gamma \right)\right]\\ \times \left[ch\left(b\gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_2\left(s\right)+{\left({\chi }_{55}^E\right)}^{-1}\\ \times \left[\begin{array}{l}{d}_{15}{E}_1\left(s\right)-\left[\gamma /\text{sh}\left(b\gamma \right)\right]\\ \times \left[\text{ch}\left(b\gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\chi }_{55}^E=s_{55}^E/S_0$

The equation of inverse piezo effect ^3–41 is written in the general form

$S_i={\nu }_{mi}{\Psi }_m+s_{ij}^{\Psi }{T}_j$

here ${\Psi }_m=E_m,D_m$ is control parameter at the voltage or current control.

At $x=0$ and $x=l$ for $l=\{\delta ,h,b$ the system of the boundary conditions for a piezoengine is obtained

$T_j\left(0,s\right)=\frac{1}{s_{ij}^{\Psi }}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=0}-\frac{{\nu }_{mi}}{s_{ij}^{\Psi }}{\Psi }_m\left(s\right)$

$T_j\left(l,s\right)=\frac{1}{s_{ij}^{\Psi }}{\frac{d\Xi \left(x,s\right)}{dx}|}_{x=l}-\frac{{\nu }_{mi}}{s_{ij}^{\Psi }}{\Psi }_m\left(s\right)$

The transform of the force causes displacement has the general form

$F\left(s\right)=\frac{{\nu }_{mi}{S}_0{\Psi }_m\left(s\right)}{s_{ij}^{\Psi }}$

The general structural model and scheme are obtained on Figure 1

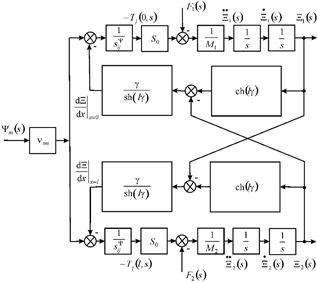
Figure 1 General scheme engine.

${\Xi }_1\left(s\right)={\left(M_1{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_1\left(s\right)+{\left({\chi }_{ij}^{\Psi }\right)}^{-1}\\ \times \left[\begin{array}{l}{\nu }_{mi}{\Psi }_m\left(s\right)-\left[\gamma /\text{sh}\left(l\gamma \right)\right]\\ \times \left[\text{ch}\left(l\gamma \right){\Xi }_1\left(s\right)-{\Xi }_2\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\Xi }_2\left(s\right)={\left(M_2{s}^2\right)}^{-1}\left\{\begin{array}{l}-F_2\left(s\right)+{\left({\chi }_{ij}^{\Psi }\right)}^{-1}\\ \times \left[\begin{array}{l}{\nu }_{mi}{\Psi }_m\left(s\right)-\left[\gamma /\text{sh}\left(l\gamma \right)\right]\\ \times \left[\text{ch}\left(l\gamma \right){\Xi }_2\left(s\right)-{\Xi }_1\left(s\right)\right]\end{array}\right]\end{array}\right\}$

${\chi }_{ij}^{\Psi }=s_{ij}^{\Psi }/S_0$

here

$v_{mi}=\{\begin{array}{c}{d}_{33},d_{31},d_{15}\\ g_{33},g_{31},g_{15}\end{array}$ ,

,${\Psi }_m=\{\begin{array}{c}{E}_3,E_3,E_1\\ D_3,D_3,D_1\end{array}$ ,$s_{ij}^{\Psi }=\{\begin{array}{c}{s}_{33}^E,s_{11}^E,s_{55}^E\\ s_{33}^D,s_{11}^D,s_{55}^D\end{array}$ ,$\gamma =\{{\gamma }^E,{\gamma }^D$ ,

$c^{\Psi }=\{c^E,c^D$

The general structural model and scheme of a piezoengine on Figure 1 are used to calculate systems in aeronautics and aerospace. The displacement matrix is written

$\left(\begin{array}{c}{\Xi }_1\left(s\right)\\ {\Xi }_2\left(s\right)\end{array}\right)=\left(W\left(s\right)\right)\left(\begin{array}{c}{\Psi }_m\left(s\right)\\ F_1\left(s\right)\\ F_2\left(s\right)\end{array}\right)$

$\left(W\left(s\right)\right)=\left(\begin{array}{c}\begin{array}{ccc}{W}_{11}\left(s\right)& W_{12}\left(s\right)& W_{13}\left(s\right)\end{array}\\ \begin{array}{ccc}{W}_{21}\left(s\right)& W_{22}\left(s\right)& W_{23}\left(s\right)\end{array}\end{array}\right)$

here its functions

$W_{11}\left(s\right)={\Xi }_1\left(s\right)/{\Psi }_m\left(s\right)={{\nu }_{mi}{}_{}^{}\left[M_2{\chi }_{ij}^{\Psi }{s}^2+\gamma th\left(l\gamma /2\right)\right]/A}_{ij}$

$\begin{array}{l}{A}_{ij}=M_1{M}_2{\left({\chi }_{ij}^{\Psi }\right)}^2{s}^4+\left\{\left(M_1+M_2\right){\chi }_{ij}^{\Psi }/{\left[c^{\Psi }\text{th}\left(l\gamma \right)\right]}^{}\right\}{s}^3+\\ +\left[\left(M_1+M_2\right){\chi }_{ij}^{\Psi }\alpha /th\left(l\gamma \right)+1/{\left(c^{\Psi }\right)}^2\right]s^2+2\alpha s/c^{\Psi }+{\alpha }^2\end{array}$

$W_{21}\left(s\right)={\Xi }_2\left(s\right)/{\Psi }_m\left(s\right)={{\nu }_{mi}{}_{}^{}{\left[M_1{\chi }_{ij}^{\Psi }{s}^2+\gamma \text{th}\left(l\gamma /2\right)\right]}^{}/A}_{ij}$

$W_{12}\left(s\right)={\Xi }_1\left(s\right)/F_1\left(s\right)=-{{\chi }_{ij}^{\Psi }{}_{}^{}\left[M_2{\chi }_{ij}^{\Psi }{s}^2+\gamma /\text{th}\left(l\gamma \right)\right]/A}_{ij}$

$\begin{array}{l}{W}_{13}\left(s\right)={\Xi }_1\left(s\right)/F_2\left(s\right)=\\ =W_{22}\left(s\right)={\Xi }_2\left(s\right)/F_1\left(s\right)={\left[{\chi }_{ij}^{\Psi }\gamma /sh\left(l\gamma \right)\right]/A}_{ij}\end{array}$

$W_{23}\left(s\right)={\Xi }_2\left(s\right)/F_2\left(s\right)=-{{\chi }_{ij}^{\Psi }{}_{}^{}\left[M_1{\chi }_{ij}^{\Psi }{s}^2+\gamma /th\left(l\gamma \right)\right]/A}_{ij}$

The settled longitudinal displacements at the voltage control are used

${\xi }_1=d_{33}U{M}_2/\left(M_1+M_2\right)$

${\xi }_2=d_{33}U{M}_1/(M_1+M_2)$

To the PZT piezoengine $d_{33}$ = 4×10^-10 m/V, $U$ = 50 V, $M_1$ = 0.5 kg, $M_2$ = 2 kg we have displacements ${\xi }_1+{\xi }_2$ = 20 nm, ${\xi }_1$ = 16 nm, ${\xi }_2$ = 4 nm with 10% error.

For the voltage control the equation of the direct piezo effect is written^8–41

$D_m=d_{mi}{T}_i+{\epsilon }_{mk}^E{E}_k$

here i, m, k are the indexes,${\epsilon }_{mk}^E$ is the permittivity. The direct coefficient $k_d$ ;for the engine at the voltage control is founded

$k_d=\frac{d_{mi}{S}_0}{\delta s_{ij}^E}$

At the voltage control the transform of the voltage for the feedback on Figure 2 is obtained

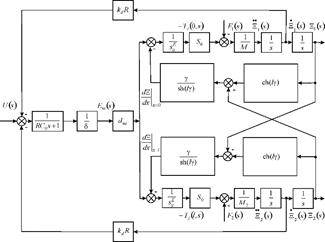
Figure 2 Scheme engine with two feedbacks.

$U_d\left(s\right)=\frac{d_{mi}{S}_{0}R}{\delta s_{ij}^E}{\stackrel{•}{\Xi }}_{{}_n}\left(s\right)=k_{d}R{\stackrel{•}{\Xi }}_{{}_n}\left(s\right)$ ,$n=1,2$

here the number $n$ of the ends engine.

Let us consider the elastic compliance of a piezoengine. At voltage control its maximum parameters are written

$T_{j\max }=E_m{d}_{mi}/s_{ij}^E$

$F_{\text{max}}=E_m{d}_{mi}{S}_0/s_{ij}^E$

At current control the maximum force is founded

$F_{\max }=\frac{U}{\delta }{d}_{mi}\frac{S_0}{s_{ij}^E}+\frac{F_{\max }}{S_0}{d}_{mi}{S}_c\frac{1}{{\epsilon }_{mk}^T{S}_c/\delta }\frac{1}{\delta }{d}_{mi}\frac{S_0}{s_{ij}^E}$

here $S_c$ , $C_0$ are the sectional area of the capacitor, its capacitance.

Then at current control the parameters are written

$T_{j\max }=\frac{E_m{d}_{mi}}{\left(1-k_{mi}^2\right)s_{ij}^E}$

$k_{mi}=d_{mi}/\sqrt{s_{ij}^E{\epsilon }_{mk}^T}$

here $k_{mi}$ is the coefficient of electromechanical coupling.

At current control of the parameters are founded

$T_{j\max }=E_m{d}_{mi}/s_{ij}^D,s_{ij}^D=(1-k_{mi}^2)s_{ij}^E$

The elastic compliance $s_{ij}$ is written $s_{ij}^E>s_{ij}>s_{ij}^D$ , here $s_{ij}^E/s_{ij}^D\le 1.2$ . Then$C_{ij}^E=S_0/\left(s_{ij}^{E}l\right)$ is the stiffness of the engine at voltage control, $C_{ij}^D=S_0/\left(s_{ij}^{D}l\right)$ is the stiffness at current control,$C_{ij}^E<C{}_{ij}<C_{ij}^D$ , $C_{ij}=S_0/\left(s_{ij}l\right)$ is a general stiffness of an engine.

The mechanical characteristic of a piezoengine ^8–41

${S_i\left(T_j\right)|}_{\Psi =const}={{\nu }_{mi}{\Psi }_m|}_{\Psi =const}+s_{ij}^{\Psi }{T}_j$

The adjustment characteristic

$S_i\left({\Psi }_m\right){\left|{}_{T=const}=v_{mi}{\Psi }_m+s_{ij}^{\Psi }{T}_j\right|}_{T=const}$

Then the mechanical characteristic is written

$\Delta l=\Delta l_{\max }\left(1-F/F_{\max }\right)$

$\Delta l_{\max }={\nu }_{mi}{\Psi }_{m}l$ ,$F_{\max }=T_{j\max }{S}_0={\nu }_{mi}{\Psi }_m{S}_0/s_{ij}^{\Psi }$

here $\Delta l_{\max }$ , $F_{\max }$ are the maximum of the displacement and the force. The transverse mechanical characteristic is founded

$\Delta h=\Delta h_{\max }\left(1-F/F_{\max }\right)$

$\Delta h_{\max }=d_{31}{E}_{3}h$ ,$F_{\max }=d_{31}{E}_3{S}_0/s_{11}^E$

To the PZT piezoengine $d_{31}$ = 2∙10^-10 m/V, $E_3$ = 0.25∙10⁵ V/m, $h$ = 2.5∙10^-2 m, $S_0$ = 1.5∙10^-5 m², $s_{11}^E$ = 15∙10^-12 m²/N the parameters are determined $\Delta h_{\max }$ = 125 nm and $F_{\text{max}}$ = 5 N with 10% error.

The relative displacement at elastic load

$\frac{\Delta l}{l}={\nu }_{mi}{\Psi }_m-\frac{s_{ij}^{\Psi }{C}_e}{S_0}\Delta l$ ,$F=C_e\Delta l$

The adjustment characteristic

$\Delta l=\frac{{\nu }_{mi}l{\Psi }_m}{1+C_e/C_{ij}^{\Psi }}$

The general elastic compliance

$s_{ij}=k_s{s}_{ij}^E$ ,$\left(1-k_{mi}^2\right)\le k_s\le 1$

The scheme on Figure 3 we have at the voltage control the piezoengine with first fixed end and elastic-inertial load.

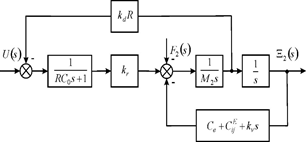
Figure 3 Scheme engine with one feedback.

The function at the voltage control with fixed first end and elastic-inertial load on second end for Figure 3 has the form

$W\left(s\right)={\Xi }_2\left(s\right)/U\left(s\right)=k_r/\left(a_3{p}^3+a_2{p}^2+a_{1}p+a_0\right)$

$a_3=R{C}_0{M}_2$ ,$a_2=M_2+R{C}_0{k}_v$

$a_1=k_v+R{C}_{0}C{}_{ij}+R{C}_{0}C{}_e+R{k}_r{k}_d$ ,$a_0=C{}_e+C{}_{ij}$

The function withis obtained

$W\left(s\right)=\frac{\Xi \left(s\right)}{U\left(s\right)}=\frac{k_{31}^U}{T_t^2{s}^2+2T_t{\xi }_{t}s+1}$

$k_{31}^U=d_{31}\left(h/\delta \right)/\left(1+C_e/C_{11}^E\right)$

$T_t=\sqrt{M_2/\left(C_e+C_{11}^E\right)}$ ,${\omega }_t=1/T_t$

To the PZT piezoengine $M_2$ = 4 kg, $C_e$ = 0.1×10⁷ N/m, $C_{11}^E$ = 1.5×10⁷ N/m the parameters are founded $T_t$ = 0.5×10^-3 s, ${\omega }_t$ = 2×10³ s^-1 with 10% error.

To $d_{31}$ = 2∙10^-10 m/V, $h/\delta$ = 22, $C_e/C_{11}^E$ = 0.1 the coefficient is determined $k_{31}^U$ = 4 nm/V with 10% error.

A piezoengine is used for aeronautics and aerospace in system of adaptive optics for compound telescope and satellite telescope, deformable mirrors, interferometers, damping vibration, astrophysics for displacements of mirrors and scanning microscopy. The structural model and scheme of a piezoengine are constructed by applied method mathematical physics. For a piezoengine its displacement matrix is obtained. The schemes with the feedbacks at the voltage control are determined.

The structural model and scheme of a piezoengine for aeronautics and aerospace are obtained taking into account equation of piezoeffects and decision wave equation. We have the general structural model and scheme of a piezoengine for the longitudinal, transverse and shift deformations. The structural scheme of the piezoactuator for longitudinal, transverse, shift piezoelectric effects at voltage control converts to the general structural scheme of the piezoactuator for aeronautics and aerospace with the replacement of the following parameters:

${\Psi }_m=E_3,E_3,E_1$ ,${\nu }_{mi}=d_{33},d_{31},d_{15}$ $s_{ij}^{\Psi }=s_{33}^E,s_{11}^E,s_{55}^E$ ,

,$l=\delta ,h,b$ .

It is possible to construct the general structural model and scheme, the transfer functions in matrix form of the piezoengine, using the solutions of the wave equation of the piezoactuator and taking into account the features of the deformations actuator along the coordinate axes. The general structural model and scheme of the piezoengine after algebraic transformations are produced the transfer functions of the piezoengine. The piezoengine with the transverse piezoeffect compared to the piezoengine for the longitudinal piezoeffect provides greater range its displacement and less force.

The general structural model model and the scheme of a piezoengine are obtained. The systems of equations are determined for the structural models of the piezoengines for aeronautics and aerospace. Using the obtained solutions of the wave equation and taking into account the features of the deformations along the coordinate axes, it is possible to construct the general structural model and scheme of a piezoengine for systems of adaptive optics and to describe its dynamic and static properties. The transfer functions in matrix form are described the deformations of the piezoengines during its operation as a part of systems of adaptive optics.

The general structural scheme and the transfer functions of a piezoengine for aeronautics and aerospace are obtained from the structural model of a piezoengine for the transverse, longitudinal, shift piezoelectric effects. The displacement matrix is founded. The parameters of the piezoengine at the voltage control are determined for aeronautics and aerospace. The static and dynamic characteristics of the PZT piezoengine are obtained.

None.

None.

The author declares that there are no conflicts of interest.

1. Uchino K. Piezoelectric actuator and ultrasonic motors. Kluwer academic publisher, Boston, MA. 350 p. 1997.
2. Afonin SM. Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Doklady Mathematics. 2006:74(3):943–948.
3. Liu Y, Zhang S, Yan P, et al. Finite element modeling and test of piezo disk with local ring electrodes for micro displacement. Micromachines. 2022;13(6):951.
4. Afonin SM. Generalized parametric structural model of a compound elecromagnetoelastic transduser. Doklady Physics. 2005;50(2):77–82.
5. Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transducer. Doklady Physics. 2008;53(3):137–143.
6. Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady Mathematics. 2006;73(2):307–313.
7. Cady WG. Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. New York: McGraw-Hill Book Company. 1946:806.
8. Mason W. Physical acoustics: Principles and methods. Vol.1. Part A. Methods and Devices. New York: Academic Press. 1964. p. 515.
9. Yang Y, Tang L. Equivalent circuit modeling of piezoelectric energy harvesters. Journal of Intelligent Material Systems and Structures. 2009;20(18):2223–2235.
10. Zwillinger D. Handbook of Differential Equations. Boston: Academic Press. 1989;673.
11. Afonin SM. A generalized structural-parametric model of an elecromagnetoelastic converter for nano- and micrometric movement control systems: III. Transformation parametric structural circuits of an elecromagnetoelastic converter for nano- and micrometric movement control systems. Journal of Computer and Systems Sciences International. 2006;45(2):317–325.
12. Afonin SM. Generalized structural-parametric model of an electromagnetoelastic converter for control systems of nano-and micrometric movements: IV. Investigation and calculation of characteristics of step-piezodrive of nano-and micrometric movements. Journal of Computer and Systems Sciences International. 2006;45(6):1006–1013.
13. Afonin SM. Decision wave equation and block diagram of electromagnetoelastic actuator nano- and microdisplacement for communications systems. International Journal of Information and Communication Sciences. 2016;1(2):22–29.
14. Afonin SM. Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. In: Ed. Parinov IA, editor. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. New York: Nova Science. 2015. pp. 225-242.
15. Afonin SM. A structural-parametric model of electroelastic actuator for nano- and microdisplacement of mechatronic system. In: Bartul Z, Trenor J, editors. Chapter 8 in Advances in Nanotechnology. New York: Nova Science. 2017;19:259–284.
16. Shevtsov SN, Soloviev AN, Parinov IA, et al. Piezoelectric actuators and generators for energy harvesting. Research and Development. Springer. 2018;182.
17. Adaptive optics - CoreMorrow. Harbin, China: CoreMorrow Ltd. 2024
18. Precision machining – CoreMorrow. Harbin, China: CoreMorrow Ltd. 2024.
19. Baraniuk R, Drossel WG. Simplification of the model of piezoelectric actuator control based on preliminary measurements. 2020;9(3):90.
20. Afonin SM. Electromagnetoelastic nano- and microactuators for mechatronic systems. Russian Engineering Research. 2018;38(12):938–944.
21. Afonin SM. Nano- and micro-scale piezomotors. Russian Engineering Research. 2012;32(7-8):519–522.
22. Afonin SM. Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers, Mechanics of Solids. 2007;42(1):43–49.
23. Afonin SM. Stability of strain control systems of nano-and microdisplacement piezotransducers. Mechanics of Solids. 2014;49(2):196–207.
24. Afonin SM. Structural-parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. International Journal of Physics. 2017;5(1):9–15.
25. Afonin SM. Structural-parametric model multilayer electromagnetoelastic actuator for nanomechatronics. International Journal of Physics. 2019;7(2):50–57.
26. Afonin SM. Calculation deformation of an engine for nano biomedical research. International Journal of Biomed Research. 2021;1(5):1–4.
27. Afonin SM. Precision engine for nanobiomedical research. Biomedical Research and Clinical Reviews. 2021;3(4):1–5.
28. Afonin SM. Solution wave equation and parametric structural schematic diagrams of electromagnetoelastic actuators nano- and microdisplacement. International Journal of Mathematical Analysis and Applications. 2016;3(4):31–38.
29. Afonin SM. Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 2018;7(1):6.
30. Afonin SM. Structural-parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 2019;8(3):52.
31. Afonin SM. Structural-parametric models and transfer functions of electromagnetoelastic actuators nano- and microdisplacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics. 2016;2(2):52–59.
32. Afonin SM. Design static and dynamic characteristics of a piezoelectric nanomicrotransducers. Mechanics of Solids. 2010;45(1):123–132.
33. Afonin SM. Electromagnetoelastic actuator for nanomechanics. Global Journal of Research in Engineering: A Mechanical and Mechanics Engineering. 2018;18(2):19–23.
34. Afonin SM. Multilayer electromagnetoelastic actuator for robotics systems of nanotechnology. Proceedings of the 2018 IEEE Conference EIConRus. 2018:1698–1701.
35. Afonin SM. A block diagram of electromagnetoelastic actuator nanodisplacement for communications systems. Transactions on Networks and Communicatio 2018;6(3):1–9.
36. Afonin SM. Decision matrix equation and block diagram of multilayer electromagnetoelastic actuator micro and nanodisplacement for communications systems. Transactions on Networks and Communications. 2019;7(3):11–21.
37. Afonin SM. Condition absolute stability control system of electromagnetoelastic actuator for communication equipment. Transactions on Networks and Communications. 2020;8(1):8–15.
38. Afonin SM. A Block diagram of electromagnetoelastic actuator for control systems in nanoscience and nanotechnology. Transactions on Machine Learning and Artificial Intelligence. 2020;8(4):23–33.
39. Afonin SM. Optimal control of a multilayer electroelastic engine with a longitudinal piezoeffect for nanomechatronics systems. Applied System Innovation. 2020;3(4):53.
40. Afonin SM. Coded сontrol of a sectional electroelastic engine for nanomechatronics systems. Applied System Innovation. 2021;4(3):47.
41. Afonin SM. Structural-parametric model actuator of adaptive optics for composite telescope and astrophysics equipment. Phy Astron Int J. 2020;4(1):18–21.
42. Afonin SM. An actuator nano and micro displacements for composite telescope in astronomy and physics research. Phy Astron Int J. 2020;4(4):165–167.
43. Afonin SM. Calculation of the deformation of an electromagnetoelastic actuator for composite telescope and astrophysics equipment. Phy Astron Int J. 2021;5(2):55–58.
44. Afonin SM. Structural scheme actuator for nano research. COJ Reviews and Research. 2020;2(5):1–3.
45. Afonin SM. Structural–parametric model electroelastic actuator nano- and microdisplacement of mechatronics systems for nanotechnology and ecology research. MOJ Eco Environ Sci. 2018;3(5):306–309.
46. Afonin SM. Electromagnetoelastic actuator for large telescopes. Aeron Aero Open Access J. 2018;2(5):270–272.
47. Afonin SM. Condition absolute stability of control system with electro elastic actuator for nano bioengineering and microsurgery. Surgery & Case Studies Open Access Journal. 2019;3(3):307–309.
48. Afonin SM. Piezo actuators for nanomedicine research. MOJ App Bio Biomech. 2019;3(2):56–57.
49. Afonin SM. Frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics. MOJ App Bio Biomech. 2019;3(6):137–140.
50. Afonin SM. A structural-parametric model of a multilayer electroelastic actuator for mechatronics and nanotechnology. In: Bartul Z., Trenor J, Editors. Chapter 7 in Advances in Nanotechnology. New York: Nova Science, 2019;22:169–186.
51. Afonin SM. Electroelastic digital-to-analog converter actuator nano and microdisplacement for nanotechnology. In: Bartul Z, Trenor J, editors. Chapter 6 in Advances in Nanotechnology. New York: Nova Science. 2020;24:205–218.
52. Afonin SM. Characteristics of an electroelastic actuator nano- and microdisplacement for nanotechnology. In: Bartul Z, Trenor J, editors. Chapter 8 in Advances in Nanotechnology. New York: Nova Science. 2021;25:251–266.
53. Afonin SM. Rigidity of a multilayer piezoelectric actuator for the nano and micro range. Russian Engineering Research. 2021;41(4):2852-88.
54. Afonin SM. Structural scheme of electroelastic actuator for nanomechatronics. In: Parinov I.A., Chang S.H. Long B.T , editors. Chapter 40 in Advanced Materials. Proceedings of the International Conference on “Physics and Mechanics of New Materials and Their Applications”, PHENMA 2019. Switzerland, Cham: Springer. 2020:487–502.
55. Afonin SM. Absolute stability of control system for deformation of electromagnetoelastic actuator under random impacts in nanoresearch. In: Parinov I.A., Chang S.H., Kim Y.H., Noda N.A, editors. Chapter 43 in Physics and Mechanics of New Materials and Their Applications. PHENMA 2020. Springer Proceedings in Materials. Switzerland:Springer,. 2021;10:519–531.
56. Afonin SM. Electroelastic actuator of nanomechatronics systems for nanoscience. Chapter 2 in Recent Progress in Chemical Science Research. 2023;6:15-27.
57. Afonin SM. Harmonious linearization of hysteresis characteristic of an electroelastic actuator for nanomechatronics systems. In: Parinov IA, Chang SH, Soloviev AN, editors. Chapter 34 in Physics and Mechanics of New Materials and Their Applications. Proceedings of the International Conference PHENMA 2021-2022. Springer Proceedings in Materials series. 2023;20:419–428.
58. Liu Y, Zhang S, Yan P, et al. Finite element modeling and test of piezo disk with local ring electrodes for micro displacement. Micromachines. 2022;13(6):951.
59. Nalwa HS. Encyclopedia of Nanoscience and Nanotechnology. American Scientific Publishers. 2019;30.