An actuator nano and micro displacements for composite telescope in astronomy and physics research

doi:10.15406/paij.2020.04.00216

eISSN: 2576-4543

Physics & Astronomy International Journal

Research Article Volume 4 Issue 4

An actuator nano and micro displacements for composite telescope in astronomy and physics research

Afonin SM

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

National Research University of Electronic Technology, MIET, Russia

Correspondence: Afonin SM, National Research University of Electronic Technology, MIET, Moscow, Russia

Received: August 12, 2020 | Published: August 31, 2020

Citation: Afonin SM. An actuator nano and micro displacements for composite telescope in astronomy and physics research. Phys Astron Int J.2020;4(4):165-167. DOI: 10.15406/paij.2020.04.00216

Download PDF

Abstract

We obtained the deformation, the structural diagram, the transfer functions and the characteristics of the actuator nano and micro displacements for composite telescope in astronomy and physics research. The mechanical and regulation characteristics of the actuator are received.

Keywords: actuator nano and micro displacements, piezo actuator, deformation, transfer function, regulation characteristic, mechanical characteristic, nano and micro displacements, composite telescope

Introduction

The electromagnetoelastic actuator nano and micro displacements at the piezoelectric, electrostriction, magnetostriction, piezomagnetic effects is used for the control system the adaptive optics of the composite telescope and the interferometer. The multilayer actuator is increased the range of the displacement from nm to tens microns.^6–31 The structural model and the structural diagram of the multilayer actuator are determined by using the equation of the electromagnetoelasticity, the differential equation and the boundary conditions of the actuator. The piezo actuator is applied in adaptive optics for composite telescope, laser systems, interferometry, scanning microscopy, nano manipulators for physics and astronomy research The electromagnetoelastic actuator is provided displacement from 1 nm to 20 μm, force 10-1000 N, response 1-10 ms.^11–31

Deformation and structural diagram of actuator

The structural diagram of the actuator for composite telescope is obtained in difference from Cady's and Mason's electrical equivalent circuits of the piezo transducer. Electromagnetoelasticity equation has the form of the equation of reverse effect for the deformation of the actuator

$S_{i} = ν_{m i} Ψ_{m} + s_{i j}^{Ψ} T_{j}$ $S_{i} = ν_{m i} Ψ_{m} + s_{i j}^{Ψ} T_{j}$ ,

where $S_{i}$ $S_{i}$ , $ν_{m i}$ $ν_{m i}$ , $Ψ_{m}$ $Ψ_{m}$ , $s_{i j}^{Ψ}$ $s_{i j}^{Ψ}$ , $T_{j}$ $T_{j}$ are the relative deformation; the module; the control parameter; the elastic compliance; the mechanical stress.¹⁰⁻²⁵ The second order linear ordinary differential equation for the actuator.^10−25,28 has the form

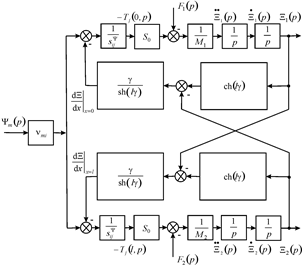
Figure 1 Structural diagram of actuator for composite telescopes in astronomy and physics research.

$\frac{d^{2} Ξ (x, p)}{d x^{2}} - γ^{2} Ξ (x, p) = 0$ $\frac{d^{2} Ξ (x, p)}{d x^{2}} - γ^{2} Ξ (x, p) = 0$ ,

where $Ξ (x, p)$ $Ξ (x, p)$ is transform of Laplace the displacement, $p$ $p$ , $γ$ $γ$ , $x$ $x$ are the parameter of transform, the propagation coefficient, the coordinate. For the structural diagram on Figure 1 and the structural model of the actuator for composite telescopes in astronomy and physics research the system of equations has the form

$Ξ_{1} (p) = (1 / (M_{1} p^{2})) \times ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ \begin{matrix} - F_{1} (p) + (1 / χ_{i j}^{Ψ}) \times [\begin{matrix} ν_{m i} Ψ_{m} (p) - [γ / sh (l γ)] \times [ch (l γ) Ξ_{1} (p) - Ξ_{2} (p)] \end{matrix}] \end{matrix} ⎫ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎭$ $Ξ_{1} (p) = (1 / (M_{1} p^{2})) \times {\begin{cases} - F_{1} (p) + (1 / χ_{i j}^{Ψ}) \\ \times [\begin{array}{l} ν_{m i} Ψ_{m} (p) - [γ / sh (l γ)] \\ \times [ch (l γ) Ξ_{1} (p) - Ξ_{2} (p)] \end{array}] \end{cases}}$ ;

$Ξ_{2} (p) = (1 / (M_{2} p^{2})) \times ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ \begin{matrix} - F_{2} (p) + (1 / χ_{i j}^{Ψ}) \times \times [\begin{matrix} ν_{m i} Ψ_{m} (p) - [γ / sh (l γ)] \times [ch (l γ) Ξ_{2} (p) - Ξ_{1} (p)] \end{matrix}] \end{matrix} ⎫ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎭$ $Ξ_{2} (p) = (1 / (M_{2} p^{2})) \times {\begin{cases} - F_{2} (p) + (1 / χ_{i j}^{Ψ}) \times \\ \times [\begin{array}{l} ν_{m i} Ψ_{m} (p) - [γ / sh (l γ)] \\ \times [ch (l γ) Ξ_{2} (p) - Ξ_{1} (p)] \end{array}] \end{cases}}$ ,

where $χ_{i j}^{Ψ} = s_{i j}^{Ψ} / S_{0}$ $χ_{i j}^{Ψ} = s_{i j}^{Ψ} / S_{0}$ , $ν_{m i} = {\begin{matrix} d_{33}, d_{31}, d_{15} d_{33}, d_{31}, d_{15} \end{matrix}$ $ν_{m i} = {\begin{matrix} d_{33}, d_{31}, d_{15} \\ d_{33}, d_{31}, d_{15} \end{matrix}$ , $Ψ_{m} = {\begin{matrix} E_{3}, E_{1} H_{3}, H_{1} \end{matrix}$ $Ψ_{m} = {\begin{matrix} E_{3}, E_{1} \\ H_{3}, H_{1} \end{matrix}$ , $s_{i j}^{Ψ} = {\begin{matrix} s_{33}^{E}, s_{11}^{E}, s_{55}^{E} s_{33}^{H}, s_{11}^{H}, s_{55}^{H} \end{matrix}$ $s_{i j}^{Ψ} = {\begin{matrix} s_{33}^{E}, s_{11}^{E}, s_{55}^{E} \\ s_{33}^{H}, s_{11}^{H}, s_{55}^{H} \end{matrix}$ , E, H are the strengths of the electric and magnetic fields.

Therefore, the system of the equations for the structural model of the actuator has the form

$Ξ_{1} (p) = (1 / (M_{1} p^{2})) \times ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \begin{matrix} - F_{1} (p) + C_{i j}^{Ψ} l \times [\begin{matrix} ν_{m i} Ψ_{m} (p) - [γ / sh (l γ)] \times [ch (l γ) Ξ_{1} (p) - Ξ_{2} (p)] \end{matrix}] \end{matrix} ⎫ ⎪ ⎪ ⎬ ⎪ ⎪ ⎭$ $Ξ_{1} (p) = (1 / (M_{1} p^{2})) \times {\begin{cases} - F_{1} (p) + C_{i j}^{Ψ} l \\ \times [\begin{array}{l} ν_{m i} Ψ_{m} (p) - [γ / sh (l γ)] \\ \times [ch (l γ) Ξ_{1} (p) - Ξ_{2} (p)] \end{array}] \end{cases}}$ ;

$Ξ_{2} (p) = (1 / (M_{2} p^{2})) \times ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \begin{matrix} - F_{2} (p) + C_{i j}^{Ψ} l \times [\begin{matrix} ν_{m i} Ψ_{m} (p) - [γ / sh (l γ)] \times [ch (l γ) Ξ_{2} (p) - Ξ_{1} (p)] \end{matrix}] \end{matrix} ⎫ ⎪ ⎪ ⎬ ⎪ ⎪ ⎭$ $Ξ_{2} (p) = (1 / (M_{2} p^{2})) \times {\begin{cases} - F_{2} (p) + C_{i j}^{Ψ} l \\ \times [\begin{array}{l} ν_{m i} Ψ_{m} (p) - [γ / sh (l γ)] \\ \times [ch (l γ) Ξ_{2} (p) - Ξ_{1} (p)] \end{array}] \end{cases}}$ ,

where $C_{i j}^{Ψ} = S_{0} / (s_{i j}^{Ψ} l) = 1 / (χ_{i j}^{Ψ} l)$ $C_{i j}^{Ψ} = S_{0} / (s_{i j}^{Ψ} l) = 1 / (χ_{i j}^{Ψ} l)$ is the stiffness of actuator.

The matrix equation of the actuator has form

$(\begin{matrix} Ξ_{1} (p) Ξ_{2} (p) \end{matrix}) = (\begin{matrix} \begin{matrix} W_{11} (p) & W_{12} (p) & W_{13} (p) \end{matrix} \begin{matrix} W_{21} (p) & W_{22} (p) & W_{23} (p) \end{matrix} \end{matrix}) ⎛ ⎜ ⎝ \begin{matrix} Ψ_{m} (p) F_{1} (p) F_{2} (p) \end{matrix} ⎞ ⎟ ⎠$ $(\begin{matrix} Ξ_{1} (p) \\ Ξ_{2} (p) \end{matrix}) = (\begin{matrix} \begin{matrix} W_{11} (p) & W_{12} (p) & W_{13} (p) \end{matrix} \\ \begin{matrix} W_{21} (p) & W_{22} (p) & W_{23} (p) \end{matrix} \end{matrix}) (\begin{matrix} Ψ_{m} (p) \\ F_{1} (p) \\ F_{2} (p) \end{matrix})$ .

From the electromagnetoelasticity equation at $F = C_{e} Δ l$ $F = C_{e} Δ l$ the regulation characteristic of the actuator has the form

$\frac{Δ l}{l} = d_{m i} Ψ_{m} - \frac{s_{i j}^{Ψ} C_{e}}{S_{0}} Δ l$ $\frac{Δ l}{l} = d_{m i} Ψ_{m} - \frac{s_{i j}^{Ψ} C_{e}}{S_{0}} Δ l$ ,

where $C_{e}$ $C_{e}$ , F are stiffness and force of the load. Therefore, the regulation characteristic of the actuator has the form

$Δ l = \frac{d_{m i} l Ψ_{m}}{1 + C_{e} / C_{i j}^{Ψ}} = k_{i j}^{Ψ} Ψ_{m}$ $Δ l = \frac{d_{m i} l Ψ_{m}}{1 + C_{e} / C_{i j}^{Ψ}} = k_{i j}^{Ψ} Ψ_{m}$ ,

$C_{i j}^{Ψ} = S_{0} / (s_{i j}^{Ψ} l)$ $C_{i j}^{Ψ} = S_{0} / (s_{i j}^{Ψ} l)$ , $k_{i j}^{Ψ} = d_{i j} l / (1 + C_{e} / C_{i j}^{Ψ})$ $k_{i j}^{Ψ} = d_{i j} l / (1 + C_{e} / C_{i j}^{Ψ})$ ,

where $C_{i j}^{Ψ}$ $C_{i j}^{Ψ}$ , $k_{i j}^{Ψ}$ $k_{i j}^{Ψ}$ are the stiffness and the transfer coefficient of the actuator. The transfer function with lumped parameter of the actuator^7,11–30 has the form

$W (p) = Ξ (p) / Ψ_{m} (p) = k_{i j}^{Ψ} / (T_{t}^{2} p^{2} + 2 T_{t} ξ_{t} p + 1)$ $W (p) = Ξ (p) / Ψ_{m} (p) = k_{i j}^{Ψ} / (T_{t}^{2} p^{2} + 2 T_{t} ξ_{t} p + 1)$ ,

$T_{t} = \sqrt{M / (C {}_{e}+ C_{i j}^{Ψ})}$ ,

where $Ξ (p)$ , $Ψ_{m} (p)$ are the transforms of the displacement and the control parameter, $T_{t}$ , $ξ_{t}$ are the time constant and the damping coefficient of the actuator, M is the load mass. The transfer function with lumped parameter of the transverse piezo actuator^7,11–30 has the form

$W (p) = Ξ (p) / U (p) = k_{31}^{U} / (T_{t}^{2} p^{2} + 2 T_{t} ξ_{t} p + 1)$ ,

$k_{31}^{U} = (d_{31} l / δ) / (1 + C_{e} / C_{11}^{E})$ , $T_{t} = \sqrt{M / (C {}_{e}+ C_{11}^{E})}$ ,

where $U (p)$ is the Laplace transform of the voltage and $k_{31}^{U}$ is the transfer coefficient. At $d_{31}$ =2×10^-10 m/V, $l / δ$ =12, M=1 kg, $C_{11}^{E}$ =3.4×10⁷ N/m, $C_{e}$ =0.2×10⁷ N/m the transfer coefficient $k_{31}^{U}$ =2.27 nm/V and the time constant $T_{t}$ =0.17×10^-3 s are obtained for the transverse piezo actuator from ceramic PZT.

From the electromagnetoelasticity equation at elastic load the regulation characteristic of the multilayer longitudinal piezo actuator is obtained in the following form

$Δ l = \frac{d_{33} n U}{1 + C_{e} / C_{33}^{E}} = k_{33}^{U} U$ ,

$k_{33}^{U} = d_{33} n / (1 + C_{e} / C_{33}^{E})$ , $l = n δ$ ,

where $k_{33}^{U}$ is the transfer coefficient.

For the multilayer longitudinal piezo actuator from ceramic PZT at $d_{33}$ =4∙10^-10 m/V, n = 6, $C_{33}^{E}$ =4∙10⁷ N/m, $C_{e}$ =0.2∙10⁷ N/m, U=100 V are received $k_{33}^{U}$ =2.29 nm/V and $Δ l$ =229 nm.

The mechanical characteristic of the actuator has form $S_{i} (T_{j})$ or $Δ l (F)$ and the regulation line of actuator has form $S_{i} (Ψ_{m})$ or $Δ l (U)$ . The mechanical characteristic is obtained in the following form

${S_{i} |}_{Ψ = const} = {d_{m i} Ψ_{m} |}_{Ψ = const} + s_{i j}^{Ψ} T_{j}$ .

The regulation characteristic of the actuator has the form

${S_{i} |}_{T = const} = d_{m i} E_{m} + {s_{i j}^{E} T_{j} |}_{T = const}$ .

The mechanical characteristic of the actuator has the form

$Δ l = Δ l_{max} (1 - F / F_{max})$ ,

$Δ l_{max} = d_{m i} Ψ_{m} l$ , $F_{max} = d_{m i} Ψ_{m} S_{0} / s_{i j}^{Ψ}$ ,

where $Δ l_{max}$ is the maximum displacement for $F = 0$ and $F_{max}$ is the maximum force for $Δ l = 0$ .

The maximum displacement and the maximum force of the transverse piezo actuator on Figure 2 have the form

$Δ h_{max} = d_{31} E_{3} h$ , $F_{max} = d_{31} E_{3} S_{0} / s_{11}^{E}$ .

At $d_{31}$ =2∙10^-10 m/V, $E_{3}$ = 2∙10⁵ V/m, h = 2.5∙10^-2 m, $S_{0}$ =1.5∙10^-5 m², $s_{11}^{E}$ =15∙10^-12 m²/N parameters of the transverse piezo actuator are found $Δ h_{max}$ =1000 nm and $F_{max}$ =40 N. The discrepancy between the experimental data for the piezo actuators and the calculation results is 10%.

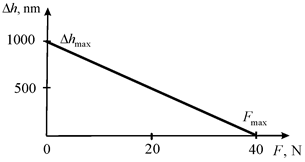
Figure 2 Mechanical characteristic of transverse piezo actuator for composite telescopes in astronomy and physics research.

Conclusion

The regulation characteristic, the transfer function and the structural diagram of the actuator nano and micro displacements are obtained for composite telescope in astronomy and physics research. The mechanical and regulation characteristics of the actuator nano and micro displacements are found for nano manipulators in physics and astronomy research. The mechanical characteristic of actuator and its maximum displacement and maximum force are obtained. For the elastic load the regulation characteristics of the electromagnetoelastic actuator and the multilayer piezo actuator are calculated.