The sufficient condition of absolute stability system with nano piezoengine by using the derivative of the hysteretic piezoengine deformation is determined for the randomly influences. The set of equilibrium positions of the piezoengine in the control system is stable relative to mathematical expectations, when the condition of absolute stability with the maximum piezo module is met. The statistical linearization method is using for the determination condition of absolute stability control system with the nano piezoengine.

Keywords: sufficient condition of absolute stability system, randomly influences, nano piezoengine, hysteresis, biomechanics

The movement nano piezoengine is achieved due to its deformation, when the electrical voltage is applied.^1–11 The nano piezoengine is used for biomechanics for scanning microscopy, nano manipulator, dosing device, nano pump.^12–27 In articles^1,3,18 the absolute stability of control system under deterministic influences is considered. The sets of equilibrium positions of the systems the piezoengines under deterministic influences are obtained in articles.^18,23 Structural models and transfer functions of the piezoengines are defined in.^5–22,24,25 In this work the absolute stability of system with the piezoengine under randomly influences is obtained for biomechanics.

The statistical linearization method is using for condition of absolute stability system with the nano piezoengine under the randomly influences for biomechanics.

The application of the criterion of absolute stability of system with the piezoengine²³ is determined for biomechanics. In this work, the Preisach hysteresis model is used.¹⁴ The hysteresis Preisach function of the relative deformation the piezoengine has the form.

$S_i=F{\left[{E_m|}_0^t,t,S_i\left(0\right),\text{sign}{\dot{E}}_m\right]}_{}^{}$

here $S_i$  - the deformation, t - time, $S_i\left(\text{0}\right)$  - the initial condition for the deformation, $E_m$  - the strength of electric field, $\text{sign}{\dot{E}}_m$  - the sign for velocity of change strength of electric field.

For the piezoengine the vertices of the basic hysteresis loops lie on the initial curve in the form $S_i=F_1\left(E_m\right)$ .²³ The initial curve^3,23 of the hysteresis deformation has the form $F_{\text{1}}\left(E_m\right)=d_{mi}^{\text{0}}{E}_m+c_{mi}{E}_m^{\text{3}}=d_{mi}^{\text{max}}{E}_m$  the maximum of the piezomodule $d_{mi}^{\max }$  has the form.

$d_{mi}^{\max }=d_{mi}^0+c_{mi}{E}_m^2$

where $d_{mi}^0$  - the initial piezomodule, $c_{mi}$  - the coefficient, $E_m$  - the strength of electric field.

From the Yakubovich criterion²³ the criterion absolute stability of control system for the nano piezoengine is obtained for biomechanics. The condition for the absolute stability of system with nano piezoengine at deterministic influences is estimated in the form.

$\mathrm{Re}{\nu }_{mi}W\left(j\omega \right)\ge -1$

here ω - the frequency, j - the imaginary unit, ${\nu }_{mi}$  - maximum of the tangent the angle of inclination to the hysteresis loop.

For the longitudinal piezoengine at deterministic influences the maximum tangent of the hysteresis deformation ${\nu }_{33}$  = 1 nm/V has the form for the longitudinal piezoeffect.

The equilibrium positions of the piezoengine in the system for controlling its deformation are stable relative to mathematical expectations, when the condition of absolute stability with the maximum piezomodule as the maximum derivative of the hysteresis characteristic is satisfied.

Let us consider the use of the statistical linearization method to calculate the stability of control system for the piezoengine with normal Gaussian distribution of random influences. For statistical linearization the derivative in general has the form.

$\frac{\partial m_{S_i}}{\partial m_{E_m}}=\frac{1}{2{\sigma }_{E_m}^2}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}}\left[S_i^{+}\left(E_m\right)+S_i^{-}\left(E_m\right)\right]\left(E_m-m_{E_m}\right)\frac{1}{{\sigma }_{E_m}\sqrt{2\pi }}{e}^{-\frac{{\left(E_m-m_{E_m}\right)}^2}{2{\sigma }_{E_m}^2}}d{E}_m$

where $S_i$  - the relative deformation, $F_1\left(E_m\right)=\left(S_i^{+}\left(E_m\right)+S_i^{-}\left(E_m\right)\right)/2$  - the initial curve, and indexes + and – are upper indexes for increase and decrease hysteresis deformation.

Then by using the equation of the initial curve, we have statistical linearization the derivative of the nonlinear relative deformation the nano piezoengine at normal Gaussian distribution of the random influences in the form.

$\frac{\partial m_{S_i}}{\partial m_{E_m}}=\frac{1}{{\sigma }_{E_m}^2}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{F}_1\left(E_m\right)\left(E_m-m_{E_m}\right)\frac{1}{{\sigma }_{E_m}\sqrt{2\pi }}{e}^{-\frac{{\left(E_m-m_{E_m}\right)}^2}{2{\sigma }_{E_m}^2}}}d{E}_m$

The derivative for the hysteresis characteristic at the mathematical expectation of the electric field strength equal to zero $m_{E_m}=0$  has form.

$\frac{\partial m_{S_i}}{\partial m_{E_m}}=\frac{1}{{\sigma }_{E_m}^2}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{d}_{mi}^{\max }{E}_m\left(E_m-m_{E_m}\right)\frac{1}{{\sigma }_{E_m}\sqrt{2\pi }}{e}^{-\frac{{\left(E_m-m_{E_m}\right)}^2}{2{\sigma }_{E_m}^2}}}d{E}_m=d_{mi}^{\max }$

Accordingly after statistical linearization the derivative of the hysteresis deformation piezoengine, the condition of absolute stability of control system with nano piezoengine under randomly influences is written as $\mathrm{Re}{d}_{mi}^{\max }W\left(j\omega \right)\ge -1$   for control system with the hysteresis characteristic at the randomly influences $g\left(t\right)=m_g\left(t\right)+g_0\left(t\right)$ , $\left|m_g\left(t\right)\right|\le R_g$ .

where $R_g$ - the upper bound, and the derivative of the hysteresis characteristic has the form.

$0<\frac{\partial m_{S_i}\left(m_{E_m},{\sigma }_{E_m}\right)}{\partial m_{E_m}}<d_{mi}^{\max }$

This expression for the derivative of the hysteretic deformation is used to the graphically illustration of the sufficient condition for the absolute stability of the control system with nano piezoengine under the randomly influences on Figure 1.

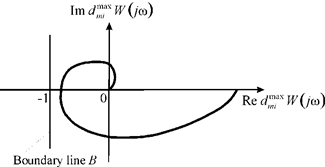
Figure 1 Sufficient condition of absolute stability system.

For the longitudinal piezoengine at the randomly influences the maximum of the piezomodule has the form $d_{33}^{\max }$  = 1.7 nm/V for the longitudinal piezoeffect.

The equilibrium positions of the piezoengine in the system for controlling its deformation are stable relative to mathematical expectations, when the condition of absolute stability with the maximum piezomodule as the maximum derivative of the hysteresis characteristic is satisfied.

The sufficient condition of absolute stability system on the derivative for the randomly influences is determined by using of the statistical linearization method. The equilibrium positions of the piezoengine in control system are stable relative to mathematical expectations. The condition for the absolute stability of the control system under random influences is obtained, taking into account the maximum piezo module of the piezoengine.

None.

None.

The authors declare that there are no conflicts of interest.

1. Yakubovich VA. Frequency conditions for absolute stability of control systems with hysteresis-like non-linearities. Dokl Akad Nauk SSSR. 1963;149(2):288–291.
2. Andrievsky BR, Barabanov AE, Bondarko VA, et al. Nonlinear systems. Frequency and matrix inequalities. Eds. Gelig AKh, Leonov GA, Fradkov AL. Fizmatlit. Moscow. 2008:608.
3. Afonin SM. Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Dokl Math. 2006;74(3):943–948.
4. Liao X, Yu P. Absolute stability of nonlinear control systems. Springer, Dordrecht. 2008:384.
5. Shevtsov SN, Soloviev AN, Parinov IA, et al. Piezoelectric actuators and generators for energy harvesting. Research and Development. Switzerland, Cham. 2018:182.
6. Afonin SM. Generalized parametric structural model of a compound elecromagnetoelastic transduser. Dokl Phys. 2005;50(2):77–82.
7. Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transducer. Dokl Phys. 2008;53(3):137–143.
8. Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Dokl Math. 2006;73(2):307–313.
9. Cady WG. Piezoelectricity: an introduction to the theory and applications of electromechancial phenomena in crystals. McGraw-Hill Book Company, New York, London. 1946:806.
10. Mason W, editor. Physical acoustics: principles and methods. Vol. 1. Part A. methods and devices. Academic press, New York. 1964:515.
11. Yang Y, Tang L. Equivalent circuit modeling of piezoelectric energy harvesters. J Intelligent Material Systems Structures. 2009;20(18):2223–2235.
12. Schultz J, Ueda J, Asada H. Cellular Actuators. Butterworth-Heinemann Publisher, Oxford. 2017:382.
13. Afonin SM. Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. Ed. Parinov IA. Nova Science, New York. 2015:225–242.
14. Preisach А. Über die magnetische nachwirkung. Zeitschrift für Physik. Berlin: Verlag von Julius Springer. 1935;94(5-6):277–302.
15. Afonin SM. Structural-parametric model multilayer electromagnetoelastic actuator for nanomechatronics. Int J Phys. 2019;7(2):50–57.
16. Afonin SM. Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 2018;7(1):1–9.
17. Afonin SM. Structural-parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 2019;8(3):1–14.
18. Afonin SM. Condition absolute stability control system of electromagnetoelastic actuator for communication equipment. Trans Networks Commun. 2020;8(1):8–15.
19. Afonin SM. Optimal control of a multilayer electroelastic engine with a longitudinal piezoeffect for nanomechatronics systems. Appl System Innovation. 2020;3(4):1–7.
20. Afonin SM. Coded сontrol of a sectional electroelastic engine for nanomechatronics systems. Appl System Innovation. 2021;4(3):1–11.
21. Afonin SM. Piezoengine for nanomedicine and applied bionics. MOJ App Bio Biomech. 2022;6(1):30–33.
22. Afonin SM. Characteristics of an electroelastic actuator nano- and microdisplacement for nanotechnology. Chapter 8 in Advances in Nanotechnology. Volume 25. Eds. Bartul Z, Trenor J, Nova Science, New York. 2021:251–266.
23. Afonin SM. Absolute stability of system with nano piezoengine for biomechanics. MOJ Appl Bio Biomech. 2023;7(1):211–213.
24. Afonin SM. Electroelastic actuator of nanomechatronics systems for nanoscience. Chapter 2 in Recent Progress in Chemical Science Research. Volume 6. Ed. Min HS, B P International, India, UK. London. 2023:15–27.
25.  Afonin SM. Harmonious linearization of hysteresis characteristic of an electroelastic actuator for nanomechatronics systems. Chapter 34 in Physics and Mechanics of New Materials and Their Applications. Proceedings of the International Conference PHENMA 2021-2022, Springer Proceedings in Materials series. Volume 20. Eds. Parinov IA, Chang SH, Soloviev AN. Springer, Cham. 2023:419–428.
26. Nalwa HS, editor. Encyclopedia of Nanoscience and Nanotechnology. Los Angeles: American Scientific Publishers. 10 Volumes. 2004.
27. Bhushan B, editor. Springer Handbook of Nanotechnology. New York: Springer. 2004:1222.