The multi-layer longitudinal piezo engine with parallel and coded control is used for nano biomedical research. The characteristics of the multi-layer longitudinal piezo engine with parallel and coded control are determined for nano biomedical research. The characteristics of the multi-layer longitudinal piezo engine are obtained by applied method of mathematical physics.

Keywords: Multi-layer longitudinal piezo engine, parallel and coded control, characteristics, biomedical research

The use of the multi-layer longitudinal piezo engine for nano- and micro displacements is promising in nano biomedical research for the compensation of gravitational and temperature deformations, precise alignment,¹⁻¹⁰ Nano pumps, microsurgery, scanning microscopy, adaptive optics, interferometers.⁸⁻³⁸

Increasing the range of displacement to tens of micrometers is achieved by using the multi-layer longitudinal piezo engine in the form the composite, stack or block piezo engine.¹⁻⁸

At present the use of the multi-layer longitudinal piezo engine with parallel and coded control is relevant, which requires determining the characteristics of this piezo engine. The application of the multi-layer longitudinal piezo engine at coded control makes it possible to effectively use electromechanical digital-to-analog conversion proportional to the control code for nano- and microdisplacements.¹¹⁻³⁴

In contrast to the simple piezo engine the multi-layer longitudinal piezo engine in static without load has the range of the movement increased in n times, where n – the number of the piezo layers. The characteristics of the multi-layer longitudinal piezo engine for parallel and coded control are calculated by applied method of mathematical physics.

Characteristics multi-layer longitudinal piezo engine at parallel control

Structurally the multi-layer longitudinal piezo engine, depending on the manufacturing technology, can be made in the form: the composite piezo engine made of individual elastically pressed piezo plates; packaged or block piezo engine made of piezo plates sintered using silver paste; the composite piezo engine made of the piezo packages with elastic reinforcement; the glued multi-layer piezo engine made of the piezo plates; the multi-layer piezo engine with the layers by using thick-film or thin-film.^1–18

The equation³⁻⁶ of the inverse longitudinal piezo effect has the form

$S_{\text{3}}=d_{\text{33}}{E}_{\text{3}}+s_{\text{33}}^E{T}_{\text{3}}$

here $S_{\text{3}},E_{\text{3}},T_{\text{3}},d_{\text{33}},s_{\text{33}}^E$ − the relative displacement, the electric field stress, the mechanical stress, the piezo module, the elastic compliance with $E=\text{const}$ , index 3 for 3 axis.

We have the equation of the mechanical characteristic at parallel control in the form $\Delta l=d_{\text{33}}nU-s_{\text{33}}^{E}Fl/S_{\text{0}}=d_{\text{33}}nU-F/C_{\text{33}}^E$ and after the transformation we have the equation of the mechanical characteristic

$\Delta l=\Delta l{}_{\text{3max}}\left(\text{1}-F/F_{\text{3max}}\right)$

$\Delta l{}_{\text{3max}}=d_{\text{33}}nU,F_{\text{3max}}=d_{\text{33}}U{S}_{\text{0}}/\left(s_{\text{33}}^E\delta \right)$

here $l=n\delta$  − the length, $C_{\text{33}}^E=S_{\text{0}}/\left(s_{\text{33}}^{E}l\right)$  − the rigidity of the of the multi-layer longitudinal piezo engine, $\Delta l$  − the displacement, $F$  − the force. Let us consider the mechanical characteristic on Figure 1 of the multi-layer longitudinal piezo engine at parallel control from ceramic PZT.

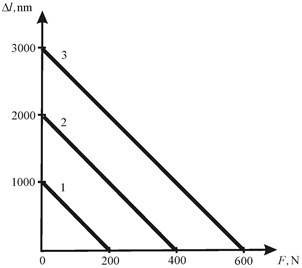
Figure 1 Mechanical characteristic of multi-layer longitudinal piezo engine at parallel control.

The measurements of the mechanical characteristic were made on the Universal testing machine UMM-5 Russia in the range of working loads under mechanical stresses in the multi layered longitudinal piezo engine up to 100 MPa. At $d_{\text{33}}$  = 0.4 nm/V, n = 50, $C_{\text{33}}^E$  = 2×10⁸ N/m for 1) U = 50 V; 2) U = 100 V; 3) U = 150 V the parameters of the multi-layer longitudinal piezo engine from ceramic PZT are determined on Figure 1 in the form 1) $\Delta l_{\text{3max}}$  = 1000 nm, $F_{\text{3max}}$  = 200 N; 2) $\Delta l_{\text{3max}}$  = 2000 nm, $F_{\text{3max}}$  = 400 N; 3) $\Delta l_{\text{3max}}$  = 3000 nm, $F_{\text{max}}$  = 600 N. The discrepancy between the experimental data and the calculation results is 10%.

The displacement of the multi-layer longitudinal piezo engine at parallel control and elastic load on Figure 2 has the form

$\Delta l=d_{\text{33}}nU-F/C_{\text{33}}^E$

$F=F_{\text{0}}+C_a\Delta l+C_e\Delta l,F_{\text{0}}={\sigma }_a{S}_{\text{0}}$

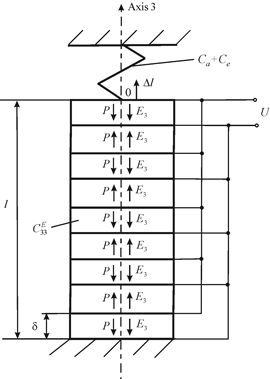
Figure 2 Multi-layer longitudinal piezo engines at parallel control and elastic load.

Here $F_{\text{0}}$  − the force of initial compression by the elastic element; ${\sigma }_a$  − the mechanical stress of the initial reinforcement in the piezo engine; $C_a$  − the rigidity of the reinforcing element; $C_e$  − the load rigidity.

Consequently, the equation for the adjustment characteristic of the multi-layer longitudinal piezo engine at parallel control and elastic load has the form

$\Delta l=\frac{d_{\text{33}}nU-{\sigma }_{a}l{s}_{\text{33}}^E}{\text{1}+\left(C_a+C_e\right)/C_{\text{33}}^E}=\frac{l\left(d_{\text{33}}{E}_{\text{3}}-{\sigma }_a{s}_{\text{33}}^E\right)}{\text{1}+\left(C_a+C_e\right)/C_{\text{33}}^E}$

For ${\sigma }_a=\text{0}$  and $C_a=\text{0}$  the equation the adjustment characteristic on Figure 3 of the multi-layer longitudinal piezo engine at parallel control and elastic load has the form

$\Delta l=\frac{d_{\text{33}}nU}{\text{1}+C_e/C_{\text{33}}^E}=\frac{\Delta l_{\text{3max}}}{\text{1}+C_e/C_{\text{33}}^E}$

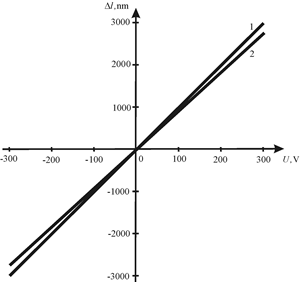
Figure 3 Adjustment characteristic at parallel control and elastic load.

The adjustment characteristics on Figure 3 are determined by using electronic measuring system of displacement Model 214 Russia for the multi-layer longitudinal piezo engine from PZT for parallel control and elastic load at $d_{\text{33}}$ = 0.4 nm/V, n = 25, $C_{\text{33}}^E$  = 4×10⁸ N/m, $C_a=\text{0}$  for 1) $C_e=\text{0}$ ; 2) $C_e$  = 0.4×10⁸ N/m with error 10%.

Characteristics multi-layer longitudinal piezo engine at coded control

The length of the multi-layer longitudinal piezo engine at coded control has the form

$l={\displaystyle \sum _{k=\text{1}}^N{l}_k=}\left({\text{2}}^N-\text{1}\right)\delta$

The maximum displacement of the multi-layer longitudinal piezo engine at coded control has the form

$\Delta l_{\max }=d_{\text{33}}\left({\text{2}}^N-\text{1}\right)U=d_{\text{33}}nU$

here $n={\text{2}}^N-\text{1}$  is the number of the piezo layers.

In static conditions at the force $F=\text{0}$ and the binary code $a_k=\text{0,}\text{1}$  we have displacement of the multi-layer longitudinal piezo engine at coded control in the form

$\Delta l={\displaystyle \sum _{k=\text{1}}^N{a}_k\Delta l_k}$

Therefore, its displacement has the form

$\Delta l={\displaystyle \sum _{k=\text{1}}^N{a}_k{d}_{\text{33}}{\text{2}}^{k-\text{1}}U=}{d}_{\text{33}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)U$

We have the mechanical characteristic at coded control¹¹⁻³⁴ in the form $\Delta l=d_{\text{33}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)U-s_{\text{33}}^{E}Fl/S_{\text{0}}=d_{\text{33}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)U-F/C_{\text{33}}^E$ after transformation, the normalized mechanical characteristic has the form

$\begin{array}{l}\Delta l/\Delta l{}_{\text{3max}}=\text{1}-F/F_{\text{3max}}\\ {\Delta }_{\text{3max}}=d_{\text{33}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)U,F_{\text{3max}}=d_{\text{33}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)U{S}_{\text{0}}/\left(s_{\text{33}}^{E}l\right)\end{array}$

here $C_{\text{33}}^E=S_{\text{0}}/\left(s_{\text{33}}^{E}l\right)$ .

Consequently, the equation for the adjustment characteristic of the multi-layer longitudinal piezo engine at coded control and elastic load on Figure 4 has the form

$\Delta l=\frac{d_{\text{33}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)U}{\text{1}+\left(C_a+C_e\right)/C_{\text{33}}^E}$

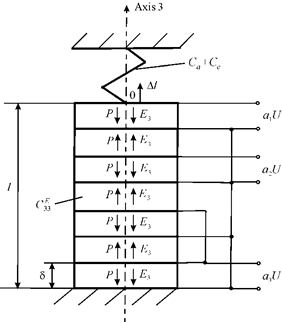
Figure 4 Multi-layer longitudinal piezo engines at coded control and elastic load.

Therefore, the displacement of the multi-layer longitudinal piezo engine elastic load has the form

$\Delta l=k_{c}U$

here $k_c$ is the coefficient

$k_c=\{\begin{array}{c}\frac{d_{\text{33}}n}{\text{1}+\left(C_a+C_e\right)/C_{\text{33}}^E}-\text{with parallel control, }\\ \frac{d_{\text{33}}\left({\displaystyle \sum _{k=\text{1}}^N{a}_k{\text{2}}^{k-\text{1}}}\right)}{\text{1}+\left(C_a+C_e\right)/C_{\text{33}}^E}-\text{with codedl control}.\end{array}$

The measurements of the parameters mechanical characteristic were made on the Universal testing machine UMM-5 Russia for the multi-layer longitudinal piezo engine from PZT for coded control at $d_{\text{33}}$ = 0.4 nm/V, n = 7, $C_{\text{33}}^E$  = 8×10⁸ N/m, and U = 200 V for 1) $a_{\text{1}}$  = 1, $a_{\text{2}}$  = 0, $a_{\text{3}}$  = 0; 2) $a_{\text{1}}$ = 1, $a_{\text{2}}$ = 1, $a_{\text{3}}$ = 0; 3) $a_{\text{1}}$ = 1, $a_{\text{2}}$ = 1, $a_{\text{3}}$ = 1. The maximum displacements and the maximum forces on Figure 5 are obtained 1) $\Delta l_{\text{max}}$  = 80 nm, $F_{\text{max}}$  = 64 N; 2) $\Delta l_{\text{max}}$  = 240 nm, $F_{\max }$ = 192 N; 3) $\Delta l_{\max }$  = 560 nm, $F_{\max }$  = 448 N with error 10%.

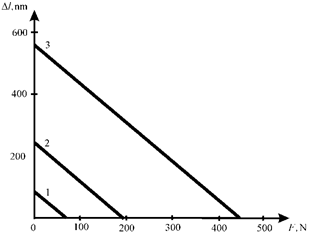
Figure 5 Mechanical characteristic at coded control.

Thus, the adjustment and mechanical characteristics of the multi-layer longitudinal piezo engine at parallel and coded control are found.

Through the use of mathematical physics we have obtained the adjustment and mechanical characteristics of the multi-layer longitudinal piezo engine at parallel and coded control for nano biomedical research. The generalized adjustment and mechanical characteristics of the multi-layer longitudinal piezo engine at parallel and coded control are determined by using the equations of the inverse longitudinal piezo effect and the mechanical force.

The multi-layer longitudinal piezo engine is used in nano biomedical research for the compensation of gravitational and temperature deformations, scanning microscopy, adaptive optics. The characteristics of the multi-layer longitudinal piezo engine at parallel and coded control are obtained by using method of mathematical physics. The parameters and the characteristics of this multi-layer longitudinal piezo engines are determined.

The adjustment and mechanical characteristics in general of the multi-layer longitudinal piezo engine at parallel and coded control are found for nano biomedical research. Future works are planned to investigate the characteristics of multi-layer piezo engines in various applications.

None.

None.

The author declares that there is no conflict of interest.

1. Uchino K. Piezoelectric actuator and ultrasonic motors. Boston, MA: Kluwer Academic Publisher. 1997:350.
2. Schultz J, Ueda J, Asada H. Cellular actuators. Butterworth-Heinemann Publisher, Oxford. 2017:382.
3. Afonin SM. Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Dokl Math. 2006;74(3):943–948.
4. Bhushan B, editor. Springer handbook of nanotechnology. New York: Springer. 2004:1222.
5. Shevtsov SN, Soloviev AN, Parinov IA, et al. Piezoelectric actuators and generators for energy harvesting. Research and Development. Springer, Switzerland, Cham. 2018:182.
6. Afonin SM. Generalized parametric structural model of a compound elecromagnetoelastic transduser. Dokl Phys. 2005;50(2):77–82.
7. Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transducer. Dokl Phys. 2008;53(3):137–143.
8. Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Dokl Math. 2006;73(2):307–313.
9. Afonin SM. Optimal control of a multilayer electroelastic engine with a longitudinal piezoeffect for nanomechatronics systems. Appl Syst Innov. 2020;3(4):1–7.
10. Afonin SM. Coded сontrol of a sectional electroelastic engine for nanomechatronics systems. Appl Syst Innov. 2021;4(3):1–11.
11. Cady WG. Piezoelectricity: an introduction to the theory and applications of electromechancial phenomena in crystals. McGraw-Hill Book Company, New York, London. 1946:806.
12. Mason W, editor. Physical acoustics: principles and methods. Vol. 1. Part A. Methods and devices. Academic Press, New York. 1964:515.
13. Liu Y, Zeng A, Zhang S, et al. An experimental investigation on polarization process of a PZT-52 tube actuator with interdigitated electrodes. Micromachines. 2022;13(10):1760.
14.  Jang Seon-Min, Yang Su Chul. Highly piezoelectric BaTiO3 nanorod bundle arrays using epitaxially grown TiO2 nanomaterials. Nanotechnology. 2018;29(23):235602.
15. Afonin SM. Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. Ed. Parinov IA. Nova Science, New York. 2015:225–242.
16. Afonin SM. Structural-parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. Int J Phy. 2017;5(1):9–15.
17. Afonin SM. Structural-parametric model multilayer electromagnetoelastic actuator for nanomechatronics. Int J Phy. 2019;7(2):50–57.
18. Afonin SM. Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 2018;7(1):1–9.
19. Afonin SM. Structural-parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 2019;8(3):1–14.
20. Afonin SM. Condition absolute stability control system of electromagnetoelastic actuator for communication equipment. Trans Netw Com. 2020;8(1):8–15.
21. Afonin SM. Rigidity of a multilayer piezoelectric actuator for the nano and micro range. Russ Engin Res. 2021;41(4):285–288.
22. Afonin SM. Structural scheme of an electromagnetoelastic actuator for nanotechnology research. Chapter 45 in Physics and Mechanics of New Materials and Their Applications. PHENMA 2023. Springer Proceedings in Materials. Vol.41. Editors Parinov IA, Chang SH, Putri EP. Springer, Cham. 2024:486–501.
23. Afonin SM. Piezoengine for nanomedicine and applied bionics. MOJ App Bio Biomech. 2022;6(1):30–33.
24. Afonin SM. System with nano piezoengine under randomly influences for biomechanics. MOJ App Bio Biomech. 2024;8(1):1–3.
25. Afonin SM. DAC electro elastic engine for nanomedicine. MOJ App Bio Biomech. 2024;8(1):38–40.
26. Afonin SM. Characteristics of an electroelastic actuator nano- and microdisplacement for nanotechnology. Chapter 8 in Advances in Nanotechnology. Volume 25. Eds. Bartul Z, Trenor J, Nova Science, New York. 2021:251–266.
27. Afonin SM. Absolute stability of system with nano piezoengine for biomechanics. MOJ App Bio Biomech. 2023;7(1):211–213.
28. Afonin SM. Structural model of nano piezoengine for applied biomechanics and biosciencess. MOJ App Bio Biomech. 2023;7(1):21–25.
29. Afonin SM. Multilayer piezo motor for nanomedicine research. MOJ App Bio Biomech. 2020;4(2):30–31.
30. Afonin SM. Characteristics electroelastic engine for nanobiomechanics. MOJ App Bio Biomech. 2020;4(3):51–53.
31. Afonin SM. Piezo actuators for nanomedicine research. MOJ App Bio Biomech. 2019;3(2):56–57.
32. Afonin SM. Structural scheme of piezoactuator for astrophysics. Phys Astron Int J. 2024;8(1):32‒36.
33. Afonin SM. Nanopiezoactuator for astrophysics equipment. Phys Astron Int J. 2023;7(2):153–155.
34. Afonin SM. Condition absolute stability of system with nano piezoactuator for astrophysics research. Aeron Aero Open Access J. 2023;7(3):99–102.
35. Afonin SM. Electroelastic actuator of nanomechatronics systems for nanoscience. Chapter 2 in Recent Progress in Chemical Science Research. Volume 6. Ed. Min HS, B P International, India, UK. London. 2023:15–27.
36.  Afonin SM. Harmonious linearization of hysteresis characteristic of an electroelastic actuator for nanomechatronics systems. Chapter 34 in Physics and Mechanics of New Materials and Their Applications. Proceedings of the International Conference PHENMA 2021-2022, Springer Proceedings in Materials series. Vol. 20. Eds. Parinov IA, Chang SH, Soloviev AN. Springer, Cham. 2023:419–428.
37. Afonin SM. Structural parametric model and diagram of electromagnetoelastic actuator for nanodisplacement in chemistry and biochemistry research. Chapter 7 in Current topics on chemistry and biochemistry. Vol 9. Ed. Baena O.J.R., B P International, India, UK. 2023:77–95.
38. Nalwa HS, editor. Encyclopedia of nanoscience and nanotechnology. Los Angeles: American scientific publishers. 2004:10.