This study analyzed the wrinkling generated in cotton fabrics after household washing and drying processes. An Automated Smoothness Analysis System (ASAS) was developed to increase the reliability of wrinkle quantification. Software developed in MATLAB processed the captured images into the equipment using Canny edge detection. Image processing proved effective, pointing out the need for a large number of visual examiners to achieve an average smoothness level similar to the calculated level by software. A design of experiments 2⁴ allowed the evaluation of the influence of different washing parameters on the wrinkling of fabrics after drying on a clothesline and in a condensation dryer. The relationship between moisture removal and smoothness level was also evaluated. The results showed that the washing load was the common factor that proved to be statistically significant for the wrinkling of the fabric after drying in a domestic dryer. Meanwhile, the number of rinses, type of centrifugation and washing load were influential parameters regarding the wrinkling of fabrics put to dry on a clothesline.

Therefore, this work provided an overview of the main parameters and levels that can excessively wrinkle the studied materials after washing and drying at home.

Keywords: measurement, image processing, wrinkling, washing parameters

Fabrics are flexible materials consisting of natural or synthetic fibers formed by various processes, including weaving, knitting, and crochet.¹ When the fabric is folded, it forms wrinkles through the action of forces imposed on the threads and fibers, as they resist the bending generated. Still, if the forces do not exceed the elasticity limit of the fibers, they can recover without permanent creasing.² During the wrinkling process, complex deformations such as bending, twisting and compression are caused to the fibers.³ The behavior of wrinkles depends on the type of fiber, the kind of yarn, the fabric's construction and the finish the textile material receives. Clothing and household items wrinkle due to their use or during washing and drying processes, and the deformation recovery is not spontaneous.⁴

Domestic washers comprise the most used means for washing clothes. In Germany, for example, more than 95% of residents use them,⁵ while in Brazil, more than 65% of the population has them.⁶ The choice of this machine is due to its practicality, time-saving, cultural and climatic issues.⁷ The washer can be classified according to the axis of rotation of the drum into the front-loading washer and top-loading washer.⁸ Various factors and parameters can affect the washing mode in these washers, including drum and agitator geometry, washing time, rotation speed, water level, water temperature, and quantity of chemicals.⁹

The drying of clothes is usually carried out in an open environment by the action of wind and sunlight. However, the improvement in living standards has made it possible for the domestic dryer to be widely used in several countries and regions of the world,¹⁰ making clothes dryers increasingly present in homes. Despite this, conventional dryers have the disadvantage of high electricity consumption.¹¹ Some parameters can evidence the performance of the domestic drying machine, such as moisture content and moisture extraction rat.¹⁰ In addition, the electric consumption of the dryer is affected by relative humidity, air mass flow, load moisture content and external temperature, factors that influence the drying performance.¹²

Cotton fabrics have different properties that make them essential in the clothing industry. However, these fabrics have the drawback of wrinkling during the domestic washing process, which is not interesting for the consumer.¹³ Different treatments have been used to produce fabrics without the presence of wrinkles. Among these treatments, chemical finishing provides greater quality, comfort, aesthetics and performance to materials.¹⁴ Different cross-linking agents and techniques have been adopted to improve the smoothness level of fabric and, consequently the angle of wrinkle recovery.^14–18

Recent studies have analyzed the wrinkling generated on fabrics by domestic washers and dryers. Higgins et al.¹⁹ observed that drying cotton fabric in a household dryer, with or without fabric softener, generally produces a higher level of smoothness than drying on a clothesline. Meanwhile, Gocek et al.²⁰ analyzed the wrinkling of pure linen fabrics after washing in a front-loading washer. They found that the highest smoothness level was obtained when there was a more significant amount of water, low mechanical rate, higher washing temperature and a higher spin speed. The drying of cotton fabric in a domestic ventilated dryer was also evaluated.²¹ A reduction in the smoothness of the cotton fabric was found regardless of the number of drying cycles, compared to the standard sample, without being washed. Finally, Liu et al.²² also evaluated the wrinkling of cotton fabric in a front-loading washer. The parameters load and centrifugation speed contributed negatively to the softness of the material. As these parameters were increased, the smoothness decreased. Lee, Yun, and Park²³ found that the smoothness level of fabrics varied according to the household dryer's rotation speed, and cotton fabrics showed less smoothness when compared to polyester fabrics.

American Association of Textile Chemists and Colorists²⁴ developed the method - AATCC 124 2009 - to measure the degree of softness in fabrics of different types of fibers. In this method, three trained observers independently assess each sample, and an average is then taken from these measurements. The proposed smoothness level ranges from one to five, with level five being smoother while level one represents a more wrinkled appearance. However, due to the subjectivity of the method, which can lead to different interpretations, some authors developed methods involving image processing techniques to quantify the wrinkling of different types of fabrics, ensuring greater accuracy and reliability to measurements.^25–27

An Automated Smoothness Analysis System (ASAS) was developed to quantify the wrinkling and support this study. This system has as differential from other studies about the conversion of the smoothness level calculated via software to the scale of the AATCC 124 method and the use of Canny edge detection and median filtering tools. In addition, this study made use of the wrinkle quantification tool developed to evaluate the main parameters of a front-loading washer that cause more significant wrinkling to cotton fabrics under different operating conditions. The wrinkling of these fabrics was analyzed also after drying in a condensation dryer and on a clothesline.

Wrinkling measurement system development

The proposed measurement system, called the Automated Smoothness Analysis System (ASAS), comprises a dark chamber (photography equipment) and its software. The photography equipment is supported by a parallelepiped-shaped structure formed by PVC pipes. The dimensions are 46 cm high, 64 cm deep and 64 cm wide. The felt of non-woven fabric covered all six faces of the parallelepiped to isolate exterior lighting. In the upper face, an aperture was inserted, which was used to manipulate the ample and the photographic camera (Figure 1). The images were captured by a Canon camera, PowerShot SX530 HS model. The photography parameter adopted were: Aperture (diaphragm) = f/4; shutter speed = 1/40 s; light sensitivity = ISO-100; resolution = 3456 x 4608 pixels (15,925,248 pixels).

Figure 1 (a) Dark chamber with equipment fixed on the upper face and the textile sample on the lower side; (b) Dark chamber fully enclosed with external illumination.

The fabrics were positioned in the lower part of the dark chamber, and a camera in the upper part captured the images. A fluorescent lamp was placed on each vertical edge, providing the proper light for capturing the image. Finally, image processing was performed to quantify the smoothness level of the samples.

Color conversion to grayscale

The primary colors RGB (red, green and blue), when combined, can reproduce a wide range of colors. However, they carry an excessive amount of information, making more computational effort to perform the image processing. Converting the RGB format to grayscale, where the image pixel intensity varies from black to white, in values from 0 to 255, respectively, causes greater computational efficiency.²⁸

Filtering process

The grayscale image is subjected to filtering processes to increase the image's visual quality by removing unwanted noises.²⁹ The median non-linear filter is usually applied to remove these noises, replacing the corrupted pixel value with the median value determined by the filter mask.³⁰ The grayscale image was filtered through the median filter with a 5x5 mask, which corresponds to the matrix size to be used in each filtered pixel. More oversized masks would result in a larger filtration. However, the choice was meticulously done so that the wrinkles themselves would not be overshadowed by the filter application.³¹ The 4x4 mask did not filter out all image noise and excessive detail, such as interlacing the warp and weft, where edge detection identified the fabric's detail as the inner edge. The 6x6 mask filtered the wrinkles themselves.

The filter acts on each matrix pixel representing the image captured in grayscale. A 5x5 mask determines that the 25 pixels of the neighborhood, including the one under analysis, are placed in ascending order. The median value of this subset is the new value that this pixel will adopt. This way, discrepant values representing noises in the image are eliminated.

Canny edge detection

With the noise eliminated and the image detail reduced, the image can have its internal edges detected through the gradients of each pixel in both directions by the first derivative of the Gaussian operator (Eq. 1).

$G^{\prime }\left(x\right)=\frac{-x}{\sqrt{2\pi {\sigma }^3}}{e}^{\frac{-x^2}{2{\sigma }^2}}$ (1)

Where x is the pixel position and σ is the first derivative of the Gaussian function.

The value defined for the σ was 12, according to visual tests where it was determined when an inner edge was no longer detected or, at the other end, when false edges were detected. Values less than 12 were responsible for false edge detection, whereas edges were neglected in detection above this value. In a single-color substrate, the existing color gradients correspond to the wrinkles. In this step, these gradients are identified as the inner edges of the image, corresponding to the fabric's wrinkles. They are characterized by a change in the gray level when there is a discontinuity in intensity or when the image gradient has a sudden variation.^32,33 In this way, the Canny edge detection operator transforms the grayscale image, previously filtered, into a black image with the inner edges in white, showing where the fabric wrinkles are arranged.

Euclidean distance

The new image, processed by this Canny edge detection, must be quantified as to the internal edges, related to wrinkles. Thus, the Euclidean distance (Eq. 121) between the image histogram and the histogram of a complete wrinkle-free image (control), which is referential, is calculated. In this processing stage, the histogram of the processed image was transformed into a matrix with two elements, the first represented by the proportion of black pixels (substrate) versus total and the second represented the proportion of white pixels (wrinkles detected by Canny).

$d(x_1,x_{2)}=\sqrt{{\displaystyle \sum }_{k=1}^{MN}{\left(x_1^k-x_2^k\right)}^2}$ (2)

Where d is the Euclidean distance,is the value referring to the pixel of the image 1 in position k;is the value referring to the pixel of image 2 in position k.

Smoothness level

This Euclidean distance is a dimensionless scalar and should be converted to the scale based on AATCC 124, ranging from 1 (very wrinkled) to 5 (without wrinkles). Several forced-binding tests were performed on the 100% cotton substrate until reaching the maximum Euclidean distance, corresponding to 1. The tests were performed using moisture and heat applied to the fabric to favor the wrinkling. The sample was compressed, crumpled and moistened for 2 minutes by a mass of 5 kg and allowed to dry so that the wrinkles would consolidate. The largest wrinkling reached was defined as the largest Euclidean distance to reach, which was converted to level 1 on the smoothness scale. The minimum Euclidean distance (zero) is equivalent to 5 (five) in the scale based on AATCC 124. This way, a linear regression was made with these two points to convert the distances into smoothness levels.

Automated smoothness analysis system vs AATCC method

The measurement system ASAS, involving all the physical equipment, such as the dark chamber, photographic equipment, and lighting, besides the software developed in MATLAB was compared to the visual methodology based on AATCC 124. This comparison aims to validate the ASAS method, showing that this system defines the fabric wrinkling on a scale from 1 to 5, as the AATCC determines, but with infinite values within this range, unlike the visual method, which stipulates only integer values. The smoothness levels of 12 random samples (100% cotton, 60 x 60 cm) were analyzed and defined by 38 evaluators. The standard substrates were wrinkled, measured and established via software at five levels: 1, 2, 3, 4 and 5, values corresponding to the AATCC 124 scale. All of them were identified with their smoothness levels to the evaluators.

Each evaluator checked the 12 samples one by one, comparing them to the five standards with known smoothness levels. All analyses were performed individually, without any external interference in determining the values.

Fabrics

The 100% cotton fabric, grammage = 135 g/m², was used in this work. In addition, the material had a canvas-like structure and were cut into 60 x 60 cm squares to simulate the size of a t-shirt. The washing load had 100% cotton fabric, canvas-like structure and 131 g/m² weight, cut into 50 x 50 cm squares to better use the acquired material.

Domestic washing process

Initially, the fabrics were washed at room temperature, 20 °C, in a front-loading washer (Electrolux, model LSI 09) with 50 mL of liquid detergent. After the washing process, the fabrics were dried in a closed room at a temperature of 21 ± 2 °C and relative humidity of 65 ± 3% and remained under these conditions for 24 hours. This procedure was performed to remove any tension in the fabrics due to the manufacturing process. After this initial washing, the materials were subjected to washing tests under different operating conditions. The washer specifications are described in Table 1, and the configurations available in the washing machine in Table 2. Cold (20° C) and hot (40° C) washing, 1 and 3 rinses and normal and turbo centrifugation were chosen to carry out the washing tests.

The water supply takes place in the front-loading washer and then the machine's mechanical agitation system, known as tipping, starts. In this system, the fabrics are directed up to a certain height in the basket and fall on each other, causing friction between the fabric and the basket and between the fabrics in the machine, providing the removal of dirt from the fabrics. In the subsequent step, the textile material is rinsed to remove the detergent used in the previous step to clean the textile article. Finally, there is the centrifugation step, which aims to deliver tissues with lower moisture content. The materials are subjected to high centrifugation speeds to extract the excess water present in the samples.

The total time of the washing, rinsing and centrifuging procedure varied according to each treatment. Washing times corresponded to 44 ± 2 minutes and 58 ± 2 minutes for temperatures of 20 and 40 °C, respectively. The rinse step required 22 ± 2 minutes when there was only one rinse. When there were three rinses, the process described was repeated, and the duration was 58 ± 2 minutes. With the increase in rinses, there is a decrease in the agitation time present in this step. The time allocated to centrifugation did not vary for the selected levels, lasting 18 ± 2 minutes. At the end of the washing procedure, the samples were dried in a domestic dryer and on a clothesline to measure the smoothness level.

Drying process

Drying was performed on a clothesline and in a domestic dryer (Electrolux, model LSI 09) to compare the wrinkling provided by the drying methods to cellulosic fiber fabrics. Drying on a clothesline took place in a closed room, with a temperature of 21 ± 2 °C and relative humidity of 65 ± 3%, and the fabrics remained under these conditions for 4 hours. The other method occurred in a condensation dryer, whose drying process occurs cyclically until the selected program ends. In the dryer, the electric heater allows the heating of the airflow. When it comes into contact with the textile material, it causes the moisture from the wet cloth evaporates into the airflow. The moist air enters a condenser, where the liquid water found in humid air will be condensed when it comes in countercurrent contact with chilled water. Finally, the air flows to the electric heater, and the cycle happens again.¹⁰ As the dryer had different drying programs, the "normal" program was selected to analyze the fabric wrinkling due to preliminary tests that indicated that it delivered the clothes dry in the shortest time. This program lasted 150 minutes and provided a maximum load temperature of 98 °C. In drying in a normal schedule, the degree of water extraction from the fabric was also quantified, according to Equation 3.

$x=\left(\frac{m_1-m_2}{m_1}\right)*100$ (3)

Where m₁ represents the mass of the fabric after the centrifugation process, in grams, and m₂ represents the mass of the fabric after the drying process, in grams.

Design of experiments

The factorial design of experiments of four factors at two levels (2⁴) was applied (Table 3). It was possible to obtain an adequate mathematical model that could predict the wrinkling behavior of cotton fabrics after the domestics washing and drying processes. Four independent variables were evaluated:

1. Washing water temperature (x₁)
2. Type of centrifugation (x₂)
3. Number of rinses (x₃)
4. Washing load (x₄).

These parameters were selected as indicated in the literature.^22,34,35 The project comprises two levels: low level, denoted -1, and high level, indicated +1. The selected levels were set according to the washer's adjustable range and following the manufacturer's suggestions. The response variables analyzed were the smoothness level of the cotton fabric (i) after the washing process in a front-loading washer and drying on a clothesline and (ii) after the washing process in a front-loading washer and drying in a condensing dryer, configuring two complete factorial designs. The experimental design resulted in 16 experiments in each design performed in triplicate, totalling 48 experiments based on each experimental design adopted.

Under the experimental conditions selected in this design of experiments, each experiment was repeated three times to analyze the error during the exploratory analysis. The design responses are determined by taking the average values of triplicate. The obtained response values were combined with a mathematical model to adjust the experimental results, which correlate with the process variables. The model used is provided in equation (Eq. 4). This model takes into account linear effects and their second and third-order interactions.

Y= b 0 + b 1 x 1 + b 2 x 2 + b 3 x 3 + b 4 x+ b 12 x 1 x 2 + b 13 x 1 x 3 + b 14 x 1 x 4 + b 23 x 2 x 3 + b 24 x 2 x 4 + b 34 x 3 x 4 + b 123 x 1 x 2 x 3 + b 124 x 1 x 2 x 4 + b 134 x 1 x 3 x 4 + b 234 x 2 x 3 x 4 +ϵ MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqkY=grVeeu0dXdh9vqqj=hEeeu0xXdbba9frFj0=OqFf ea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaaeaaaaaa aaa8qacaWGzbGaeyypa0JaaiiOaiaadkgapaWaaSbaaSqaa8qacaaI WaaapaqabaGcpeGaey4kaSIaamOya8aadaWgaaWcbaWdbiaaigdaa8 aabeaak8qacaWG4bWdamaaBaaaleaapeGaaGymaaWdaeqaaOWdbiab gUcaRiaadkgapaWaaSbaaSqaa8qacaaIYaaapaqabaGcpeGaamiEa8 aadaWgaaWcbaWdbiaaikdaa8aabeaak8qacqGHRaWkcaWGIbWdamaa BaaaleaapeGaaG4maaWdaeqaaOWdbiaadIhapaWaaSbaaSqaa8qaca aIZaaapaqabaGcpeGaey4kaSIaamOya8aadaWgaaWcbaWdbiaaisda a8aabeaak8qacaWG4bGaey4kaSIaamOya8aadaWgaaWcbaWdbiaaig dacaaIYaaapaqabaGcpeGaamiEa8aadaWgaaWcbaWdbiaaigdaa8aa beaak8qacaWG4bWdamaaBaaaleaapeGaaGOmaaWdaeqaaOWdbiabgU caRiaadkgapaWaaSbaaSqaa8qacaaIXaGaaG4maaWdaeqaaOWdbiaa dIhapaWaaSbaaSqaa8qacaaIXaaapaqabaGcpeGaamiEa8aadaWgaa WcbaWdbiaaiodaa8aabeaak8qacqGHRaWkcaWGIbWdamaaBaaaleaa peGaaGymaiaaisdaa8aabeaak8qacaWG4bWdamaaBaaaleaapeGaaG ymaaWdaeqaaOWdbiaadIhapaWaaSbaaSqaa8qacaaI0aaapaqabaGc peGaey4kaSIaamOya8aadaWgaaWcbaWdbiaaikdacaaIZaaapaqaba GcpeGaamiEa8aadaWgaaWcbaWdbiaaikdaa8aabeaak8qacaWG4bWd amaaBaaaleaapeGaaG4maaWdaeqaaOWdbiabgUcaRiaadkgapaWaaS baaSqaa8qacaaIYaGaaGinaaWdaeqaaOWdbiaadIhapaWaaSbaaSqa a8qacaaIYaaapaqabaGcpeGaamiEa8aadaWgaaWcbaWdbiaaisdaa8 aabeaaaOqaa8qacqGHRaWkcaWGIbWdamaaBaaaleaapeGaaG4maiaa isdaa8aabeaak8qacaWG4bWdamaaBaaaleaapeGaaG4maaWdaeqaaO WdbiaadIhapaWaaSbaaSqaa8qacaaI0aaapaqabaGcpeGaey4kaSIa amOya8aadaWgaaWcbaWdbiaaigdacaaIYaGaaG4maaWdaeqaaOWdbi aadIhapaWaaSbaaSqaa8qacaaIXaaapaqabaGcpeGaamiEa8aadaWg aaWcbaWdbiaaikdaa8aabeaak8qacaWG4bWdamaaBaaaleaapeGaaG 4maaWdaeqaaOWdbiabgUcaRiaadkgapaWaaSbaaSqaa8qacaaIXaGa aGOmaiaaisdaa8aabeaak8qacaWG4bWdamaaBaaaleaapeGaaGymaa WdaeqaaOWdbiaadIhapaWaaSbaaSqaa8qacaaIYaaapaqabaGcpeGa amiEa8aadaWgaaWcbaWdbiaaisdaa8aabeaak8qacqGHRaWkcaWGIb WdamaaBaaaleaapeGaaGymaiaaiodacaaI0aaapaqabaGcpeGaamiE a8aadaWgaaWcbaWdbiaaigdaa8aabeaak8qacaWG4bWdamaaBaaale aapeGaaG4maaWdaeqaaOWdbiaadIhapaWaaSbaaSqaa8qacaaI0aaa paqabaGcpeGaey4kaSIaamOya8aadaWgaaWcbaWdbiaaikdacaaIZa GaaGinaaWdaeqaaOWdbiaadIhapaWaaSbaaSqaa8qacaaIYaaapaqa baGcpeGaamiEa8aadaWgaaWcbaWdbiaaiodaa8aabeaak8qacaWG4b WdamaaBaaaleaapeGaaGinaaWdaeqaaOWdbiabgUcaRmrr1ngBPrwt HrhAXaqeguuDJXwAKbstHrhAG8KBLbacfiGae8x9dipaaaa@B839@ (4)

Where x (i =1, 2, 3 and 4) corresponds to the coded form of the independent variables, b₀ represents the mean of the results of the experimental design, b_i (i = 1, 2, 3 and 4) represents the main effect, b_ij ( i = 1, 2, 3, and 4, j = 2, 3 and 4) represents the second-order interactions and b_ijk (i = 1, 2, 3, and 4, j = 2, 3 and 4, k = 3 and 4) represents the third-order interactions and ε corresponds to the experimental error.

Analysis of variance (ANOVA) determined the agreement of the theoretical model obtained with the experimental data. For this, a confidence interval of 95% was used. The statistical software used was Statistica® 13.0 (version for Windows) (Statsoft). In addition, the adequacy of the model was tested using the regression coefficient (r²).

Wrinkling measurement system development

In a preliminary visual evaluation, it is possible to notice that the 100% cotton fabric (Figure 2a) shows a rather wrinkled surface. At the same time, it is still impossible to know what smoothness level it is. The grayscale transformation (Figure 2b) and the median filter (Figure 2c) were applied as processing steps before the Canny edge detection (Figure 2d), where the wrinkles are marked white and the background, which contains no color gradients to the point of having black borders. It's possible to observe the acuity with which the wrinkles were identified, as this process located color gradients on the pixels and delimited them as internal borders. The control image, which compares Euclidean distance, presents a black image processed by Canny edge detection, since theoretically, it comes from a substrate without wrinkles, with a smoothness level equal to 5.

Figure 2 (a) Captured image; (b) Grey scale; (c) Median filer; (d) Canny edge detection.

For this specific sample, the Euclidean distance was calculated in the software as 0.0244, and the value of the corresponding smoothness level of the AATCC 124 scale was 1.95, representing a very wrinkled fabric.

The maximum Euclidean distance between the black control image of wrinkles and a hypothetical image composed 100% by edges, that is, white in its entirety, is 2, or 1.41, which is the distance between the matrices [1, 0] and [0,1]. The two values of each matrix represent the proportion of black and white about the total of pixels. The maximum Euclidean distance attained with several tests of forcing wrinkling of the textile substrate was 0.032, which corresponds to 1 at the smoothness level in the scale of the AATCC (very wrinkled). As the smoothness level, 5 of the AATCC scale corresponds to a completely smooth material, and regression resulted in equation (Eq. 5) for converting the Euclidean distance into smoothness level.

$SL=-125d+5$ (5)

Where SL is the smoothness level and d is the Euclidean distance.

Automated smoothness analysis system vs AATCC 124 method

From 12 samples measured by 38 examiners: professors and students of the Engineering Department of the University, who are part of the academic community with domestic and professional experience in the textile area. Only one sample had unanimity (J) at the smoothness level. Of the others, two presented two different levels (K and L), six were classified into three distinct levels (A, B, D, E, F, and G) and three samples obtained four of five possible levels (C, H and I) (Table 4). This shows the lack of reliability in the methodology determined by the AATCC 124, which can be improved with the training of the examiners.

On the other hand, the software defined only one value for each sample, not necessarily an integer, related to processing the captured image that resulted in the Canny edge detection. People can evaluate only 5 possible values, while the software sets infinite numbers between 1 and 5. The correlation between the two methodologies is shown in Figure 3 (r = 0,9292). There is a correlation between the two methods, with some points not too far from the generated line, due to experimental errors in both cases. To achieve this correlation between the two methodologies, it was necessary a large number of evaluators so that the average of the smoothness levels determined by them presented consistency with the value calculated by the software.

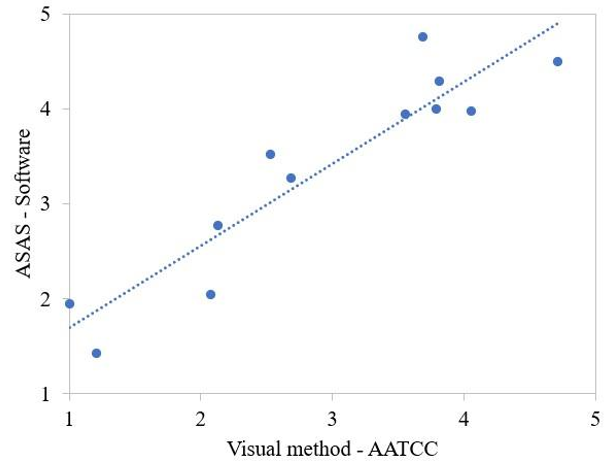
Figure 3 Correlation between the smoothness levels of the ASAS (by software) and the AATCC visual method.

It can be observed in the region between the levels 2 and 4, determined by the software, that there is a disagreement with the levels defined by the evaluators, with the points farthest from the total correlation line. This shows the importance of a digital image processing system for measuring the textile materials' smoothness levels. On the other hand, in the lower and upper limits (next to values 1 and 5), there is greater ease in the visual evaluation because the substrate is closer to the absence of wrinkles or a substantial amount of them.

Design of experiments

The effect of temperature (x1), spin (x2), number of rinses (x3), load (x4) and their interactions on the smoothness level of cotton fabrics were investigated using a complete factorial design (Table 3). Figure 4 shows the results obtained from kneading the washed cotton fabrics under different washing conditions and dried in a domestic dryer and on a clothesline.

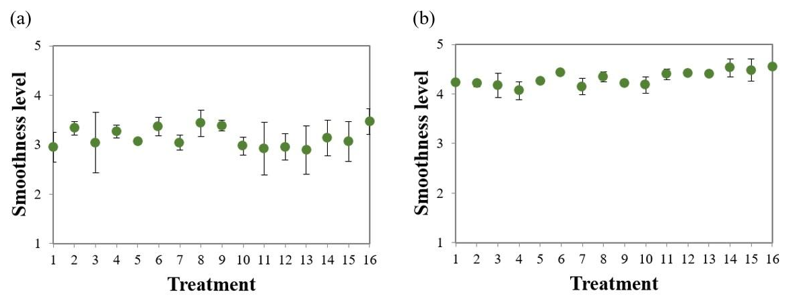
Figure 4 Smoothness level of fabrics (a) after domestic drying and (b) after drying on a clothesline.

The textile substrates had different smoothness levels after being dried on a clothesline and in a domestic dryer. Samples dried in a household dryer showed a more significant number of wrinkles. There was direct contact between the fabrics, rubbing them and the effect of the weight of the materials inside the equipment. The complex dynamics of the machine drying process also contributed to the lower softness of the fabrics of the cellulosic fibers studied. When analyzing the standard deviation, it is observed that the wrinkling caused after drying on a clothesline has less variability in the data because in this type of drying, there is no temperature variation, and the fabrics are influenced by the gravitational force, which realigned the fibers, leaving them less wrinkled.

Cellulosic fibers are formed by a semi-crystalline structure of cellulose chains, whose amorphous areas suffer more significant deformation with water penetration. The fabrics, when extended, can have a greater alignment of their cellulosic chains, which reflects in a visibly less wrinkled conformation in both materials. When the fabrics were machine dried, there was a more significant number of wrinkles. The greater smoothness of cotton fiber is related to a large amount of lignin and hemicellulose.³⁶ Lignin is hydrophobic, and the relationship between lignin and hemicellulose, which is hydrophilic, determines the amount of water that can enter the fiber and thus ensure softness and flexibility to the fiber.²

After drying in a domestic dryer, the centrifugation and washing load were the statistically significant factors at the 5% significance level for the wrinkle formed in the cotton fabric. Meanwhile, rinsing, loading and centrifugation were the statistically significant factors for the smoothness level of the cotton fabric after drying on a clothesline (Table 5).

The number of rinses was statistically significant for the wrinkling of cotton fabrics after drying on a clothesline. The increase in rinses caused the material to be in more contact with water, thus incorporating a more considerable amount of liquid. Water acted as a plasticizer, causing the fiber to be lubricated.

Fibers of vegetable origin have the semi-crystalline cellulose molecule in their structure, which has an affinity for water molecules. In addition, it has lateral hydroxyl groups in its structure that can form hydrogen bonds with water molecules. When the water molecules come in contact with the fibers, they adhere strongly to the hydrophilic groups, and the other water molecules will be indirectly absorbed by other groups that have an affinity, in a more freeway, or they can connect to the already absorbed water molecules.³⁷

Centrifugation was a significant factor in the wrinkling of the cotton fabric after the two drying processes. As the rotation speed increased from normal to turbo level, there was a small improvement in the visual appearance of the cotton fabric. After drying on a clothesline for the wrinkling of the linen fabric, the centrifugation was also significant, demonstrating a negative correlation. That is, the faster the centrifugation, the lower the smoothness of the linen fabric.

The results found for the type of centrifugation factor are due to the proximity between the levels studied, which made the fabric follow the movement of the rotating drum along the wall due to the high rotation speed for both centrifugation levels. The variation found between the wrinkling values of linen and cotton fabrics between the designs in which this factor was statistically significant for centrifugation was small. That is, the wrinkling values for both levels studied were very similar. When analyzing the rotation speed, Yu et al.³⁸ found that higher rotation speeds caused the fabrics to rest on the rotating drum wall and rotate according to the rotation of the drum and wrinkle less. On the other hand, for lower speeds, the fabrics behaved most of the time as rigid bodies in the lower portion of the drum and presented a more significant number of wrinkles.

The washing load influenced the visual appearance of the cotton fabric after drying in a domestic dryer and on a clothesline. For the wrinkling generated after drying in a domestic dryer, it was found that the increase of 2 kg in the washing load was sufficient for there to be a decrease in the smoothness level of the cotton fabrics drying in a domestic dryer. Samples in contact with a higher wash load were more wrinkled. When the materials were dried in a domestic dryer, 75% of the nominal capacity of the domestic dryer was filled, which contributed to the reduction of free space inside the machine, making the fabrics unable to move easily.

The way the fabrics move during drying inside the drum affects the heat and mass transfer rates. Furthermore, the fabrics tend to wrinkle due to their movement and consequent distribution in the dryer. Yu et al.³⁸ also observed that the materials presented better smoothness for a lower drying load. They had free space to move without causing friction between them, thus changing the smoothness of the fabric, and causing fewer wrinkles to be fixed. The samples were tangled with a more significant load, causing a minor softness.

The increase in the washing load caused an increase in the smoothness of the cotton fabric after drying on a clothesline. This decrease in fabric wrinkling is due to an ample free space in the domestic washer even with 4 kg of a washing load, which corresponds to 45% of the washer's nominal capacity, resulting in lower pressure and fewer wrinkles. Thus, there was a large volume to be occupied by the samples during the washing process. After the fabrics were washed, they were dried on a clothesline under controlled conditions, which also contributed to the softness of the cotton fabric.

Mathematical model development

From the design of experiments, it was possible to obtain a mathematical model to predict the wrinkling behavior of cotton fabrics after washing and drying processes at home. The linear polynomial equations with the statistically significant effects at the 95% confidence level obtained for the two-factorial design of experiments performed with the independent variables and their second and third-order interactions to calculate the response: fabric smoothness level (SL). The SL was obtained after capturing the sample image in a dark chamber, and subsequent treatment in the ASAS, which allowed to determine the SL of the fabrics washed and dried under certain conditions, as shown in Table 3. The equations describe, respectively, (i) the smoothness level obtained by the cotton fabric after drying in a dryer (r² = 0.8033), (ii) the smoothness level obtained by the cotton fabric after drying on a clothesline (r² = 0.9484). The equations (Eq. 6 and Eq. 7) were built from the experimental results implemented in the Statistica 13.0 software (StatSoft).

$S{L}^{\left(i\right)}=3.2022+0.1257x_2-0.0786x_4+0.1183x_1{x}_3+0.0708x_2{x}_3+0.0825x_2{x}_3{x}_4$ (6)

$\begin{array}{l}S{L}^{ii}=4.3205+0.0212x_2+0.0925x_3+0.0622x_4+0.0781x_1{x}_3+0.0219x_1{x}_4\\ -0.0404x_2{x}_3+0.0396x_2{x}_4+0.0207x_1{x}_2{x}_4-0.0472x_2{x}_3{x}_4\end{array}$ (7)

Where x₁ represents the water temperature, x₂ corresponds to the centrifugation, x₃ is number of rinses and x₄ represents the load.

The construction of mathematical models to predict the wrinkling behavior of fabrics after washing and drying processes as a function of variables such as temperature, centrifugation and washing load provides a basis for the development of algorithms that can be used in automatic control systems in textile processing industries.

ANOVA analyzed the competence and significance of the suggested models. The ANOVA results revealed that the models for the smoothness of both cotton fabrics after drying in a domestic dryer showed good fits. The models proposed to explain the wrinkling of cotton fabrics after the drying process on a clothesline showed excellent adjustments. Both models were able to explain the variability found in the processes. The coefficients of determination were above 80% for SL after drying in a dryer and above 90% after drying on a clothesline, indicating that the mathematical models with linear and interaction terms could adequately predict SL.

Analysis of the relationship between factors

Figure 5 shows the smoothness level response surfaces for the relationship with the most significant effect on the dependent variable, SL, in the two factorial designs studied.

In Figure 5a the factors selected to be analyzed were centrifugation and washing load, as they had the most significant effect on the SL of the cotton fabric after being dried in a domestic dryer. Centrifugation showed a positive correlation with the SL. Still, it is worth noting that there was only a small improvement when the centrifugation was changed from the normal level to the turbo level, as discussed in previous sections. On the other hand, the washing load presented a negative correlation with the SL. As the load was increased, the fabrics became more confined and had less space to move inside the domestic dryer, which was at ¾ of its capacity rated capacity filled. Thus, the large filling of the domestic dryer caused a lesser SL to the analyzed cotton fabrics, according to the factors enumerated and already discussed.

In Figure 5b it can be seen how the interaction between the number of washes and load capacity affects the SL of the cotton fabric after drying on the clothesline. These factors were selected to be analyzed in the response surface graph, as they were statistically significant at the 5% significance level and had the greatest effect on cotton SL after drying on the clothesline, as shown in Table 5, resulting in a moderate slope of the plane. When analyzing the number of rinses, there appears to be a positive correlation between this factor and the dependent variable, SL. The greater the amount of water in contact with the fabric, the greater the level of SL obtained, corresponding to the smoother fabric. This fact is related to the plasticizing effect of the water molecule, which provided sufficient lubrication to guarantee a higher SL when in contact with the fibers present in the cotton fabric. On the other hand, the washing load presented a positive correlation with the SL. That is, the more significant amount of load had a positive effect on the SL of the samples. However, it is worth noting that after the samples were washed inside the machine, in a confined space, they were put to dry on a clothesline. Thus, as reported in the item Experimental Design, the fabrics had their fibers realigned through the action of gravitational force, causing an effective improvement in the SL of cotton fabrics. It should also be noted that both the increase in the number of rinses and the increase in the washing load provided an increase in the SL of the fabrics, as can be seen in the graph in the region demarcated with the dark red color (SL > 4.4). In general, after drying in a dryer, the SL presented smaller, more crumpled grades, with SL close to grade 3. This evident difference in the wrinkling of the cotton samples was due to the domestic dryer's movements imposed on the fabric, different temperature gradients throughout the drying cycle, prolonged drying time, and drying load that allowed constant fiber-to-fiber friction between the fabrics.

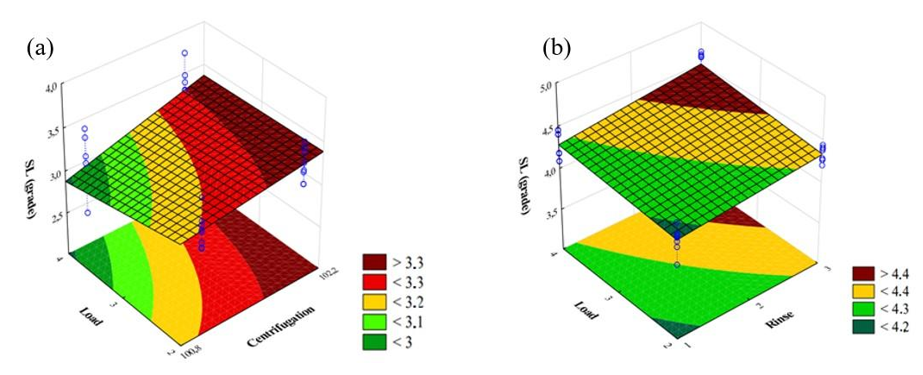
Figure 5 Response surface for the standardized effects of the most significant factors for SL of cotton fabric after drying in (a) dryer, (b) clothesline.

Relation between smoothness level and degree of water extraction

The water extraction in the "normal" domestic dryer program was related to the smoothness behavior obtained in this drying cycle, as shown in Figure 6. The fabric put to dry in the dryer already had less water, as much of the water already had been removed in the centrifugation step. The higher temperature provided by the dryer caused the residual water found in the fabric to be extracted.

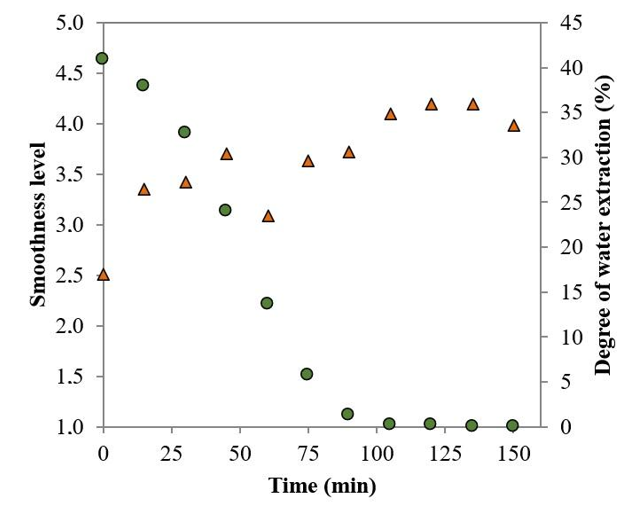
Figure 6 Relationship between the smoothness level (triangle symbols) and the degree of water extraction (circle symbols) in the dryer in the normal program.

The drying process in the normal program provided the fabric with a wrinkled appearance of about 40% of the dryer's maximum capacity, even with a load of 2 kg due to the duration of its drying cycle, which lasted for 150 minutes. In addition, the samples remained for most of this period subjected to temperatures close to 100 °C. The lower load allowed the fabrics a better movement inside the dryer. However, the samples were subjected to longer drying periods at higher temperatures. The arrangement of the material inside the dryer and this program's extended drying time helped fix the wrinkles. The high temperature the normal program provided also helped break the hydrogen bonds of the water molecule that bonded to the fiber. In addition, the wrinkles formed in the washing process lasted in greater quantity because when extracting more water, the fibers rubbed without the plasticizing action of water, which minimized fiber-to-fiber friction.

When the fabrics were dried in a domestic dryer, the water was evaporated by the action of the hot air flow, which allowed the evaporation of the water found in the damp fabric. When comparing the smoothness level of the samples after the washing and drying processes, it was found that there was an improvement in the smoothness of the fabrics after drying. However, there was no linear relationship between the processes, with no dependence on the smoothness level between the steps. Some factors may have influenced the greater wrinkling of the fabric after washing in the machine. Washing in a tipping system meant the fabrics were in constant contact with other fabrics and the domestic washer's rough surface. The drop provided by the washing system to textile substrates also contributed to reducing the fabric's smoothness. The dynamics of the washing machine in the centrifugation stage was another factor that contributed to the more severe wrinkling of fabrics, which suffered the action of higher centrifugal forces to extract the water absorbed by the fabric in the washing process.

The capture of the photographs of the textile samples in the darkroom with uniform illumination, along with its processing in software programmed in MATLAB, was proposed as an alternative method to that adopted by the AATCC 124. The technique resulted in greater reliability in the measurement of the level of smoothness, having in the Canny edge detection the key step for the measure of wrinkles. The comparison with the methodology adopted by the AATCC 124 by visual evaluations showed that the greater reliability of the method ASAS through image processing software is due to a high standard deviation in the smoothness level determined for each sample in the visual analysis, emphasizing the need for a large number of examiners to reach a value close to that calculated by the software, with the average of these evaluations.

The Automated Smoothness Analysis System was able to quantify the wrinkling of cotton fabrics after washing and drying in domestic machines, in addition to drying on a clothesline. This way, it was possible to determine the factors that affected the cause of wrinkling in these fabrics and, with that, help machine manufacturers develop machines and processes capable of causing a smaller number of wrinkles in textile items.

For future studies, it is suggested to study other factors that may influence the wrinkling of textile materials during household washing: water level and washing time, for example. Besides cotton, it is important to study other types of fibers that make up the fabric, such as one of synthetic origin, for example. It is also suggested to study the wrinkling of other fabric weaving patterns besides the plain weave, such as twill and satin.

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the National Council for Scientific and Technological Development (CNPq).

None.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

1. Li Y, Zhou L, Zhang G, et al. Study on the effects of the characteristics of textile substrates on the photonic crystal films and the related structural colors. Surf Coat Technol. 2017;319:267–276.
2. Timár–Balazsy Á, Eastop D. Chemical principles of textile conservation. Routledge; 2012.
3. Fan J, Hunter L. Engineering apparel fabrics and garments. Woodhead Publishing Limited, the Textile Institute; 2009.
4. Sinclair R. Textiles and fashion materials, design and technology. Elsevier; 2014.
5. Ellmer K, Fuchs M, Bauer U, et al. Research project Simulation Wäschepflege – Recommendations for improving resource efficiency in the laundry process in households in Germany. J Clean Prod. 2017;153:539–547.
6. Pesquisa de posse e hábitos de uso de equipamentos elétricos na classe residencial. 2019.
7. Ward D. Modelling of a horizontal–axis domestic washing machine. The Journal of The Textile Institute. 2000;91(2):207–234.
8. Bueno L, Laso C, Amador C, et al. Modelling the kinetics of stain removal from knitted cotton fabrics in a commercial Front Loader Washing Machine (FLWM). Chem Eng Sci. 2019;200:176–185.
9. Campos LGC, Hermes CJL. Experimental evaluation and transient simulation of detergent transport in household vertical axis washing machines. Chemical Engineering Research and Design. 2016;109:720–729.
10. Zhao J, Jian Q, Zhang N, et al. The improvement on drying performance and energy efficiency of a tumbler clothes dryer with a novel electric heating element. Appl Therm Eng. 2018;128:531–538.
11. Stawreberg L, Nilsson L. Potential energy savings made by using a specific control strategy when tumble drying small loads. Appl Energy. 2013;102:484–491.
12. Ma S–S, Tseng C–Y, Jian Y–R, et al. Utilization of waste heat for energy conservation in domestic dryers. Energy. 2018;162:185–199.
13. Wang L, Zheng Q, Xu P, et al. Amphiphilic alginate stabilized UV–curable polyurethane acrylate as a surface coating to improve the anti–wrinkle performance of cotton fabrics. Prog Org Coat. 2022;162:106595.
14. Karthik T, Rathinamoorthy R, Murugan R. Enhancement of wrinkle recovery angle of cotton fabric using citric acid cross–linking agent with nano–TiO2 as a co–catalyst. Journal of Industrial Textiles. 2011;42(2):99–117.
15. Liang T, Yan K, Zhao T, et al. Synthesis of a low–molecular–weight copolymer by maleic acid and acrylic acid and its application for the functional modification of cellulose. Cellulose. 2020;27(10):5665–5675.
16. Lou J, Wang D, Yuan J, et al. Improving the anti–wrinkle and hydrophilicity performance of cotton fabric via crosslinking cellulose with carboxylated polyaldehyde trehalose. Cellulose. 2021;28(8):5135–5149.
17. Mostafa K, Ameen H, Morsy M, et al. Production of high–performance textiles via pioneering strengthening approach using starch nanoparticles. Journal of Industrial Textiles. 2019;50(3):278–292.
18. Nourbakhsh S, Parvinzadeh M, Jafari S. Comparison between nano and micro silicon softener on corona discharge–treated cotton fabric. Journal of Industrial Textiles. 2017;47(7):1757–1768.
19. Higgins L, Anand S, Holmes D, et al. Effects of various home laundering practices on the dimensional stability, wrinkling, and other properties of plain woven cotton fabrics: Part II: Effect of rinse cycle softener and drying method and of tumble sheet softener and tumble drying time. Textile Research Journal. 2003;73(5):407–420.
20. Gocek I, Sahin UK, Erdem I, et al. A study on easy–care laundering of linen fabrics. Textile Research Journal. 2013;83(18):1961–1973.
21. Wei Y, Gong RH, Ning L, et al. Research on physical properties change and damage behavior of cotton fabrics dried in drum–dryer. The Journal of The Textile Institute. 2018;109(1):121–132.
22. Liu H, Gong H, Xu P, et al. The mechanism of wrinkling of cotton fabric in a front–loading washer: The effect of mechanical action. Textile Research Journal. 2019;89(18):3802–3810.
23. Lee J, Yun C, Park CH. Effect of fabric characteristics and drum rotation speeds on the movements and drying performances of clothes in a tumble dryer. Fibers and Polymers. 2022.
24. American Association of Textile Chemists and Colorists – AATCC. AATCC Technical Manual. American Association of Textile and Colorists; 2010.
25. Abril HC, Millan MS, Valencia E. Influence of the wrinkle perception with distance in the objective evaluation of fabric smoothness. Journal of Optics A: Pure and Applied Optics. 2008;10(10):1–10.
26. Liu C, Fu Y, Wu N. Novel testing equipment for fabric wrinkle resistance simulating actual wear. Textile Research Journal. 2014;84(10):1059–1069.
27. Zaouali R, Msahli S, Sakli F. Fabric wrinkling evaluation: a method developed using digital image analysis. Journal of the Textile Institute. 2010;101(12):1057–1067.
28. Cui B, Créput J–C. A systematic algorithm for moving object detection with application in real–time surveillance. SN Comput Sci. 2020;1(2):1–17.
29. Ma C, Lv X, Ao J. Difference based median filter for removal of random value impulse noise in images. Multimed Tools Appl. 2019;78(1):1131–1148.
30. Gonzalez RC, Woods RE. Digital image processing. 3rd ed. Pearson Prentice Hall; 2008.
31. Verma K, Singh BK, Thoke AS. An enhancement in adaptive median filter for edge preservation. Procedia Comput Sci. 2015;48(Iccc):29–36.
32. Qin X. A modified Canny edge detector based on weighted least squares. Comput Stat. 2021;36(1):641–659.
33. Soares LB, Oliveira J, da Costa EAC, et al. An energy–efficient and approximate accelerator design for real–time canny edge detection. Circuits Syst Signal Process. 2020;39:6098–6120.
34. Carvalho Neto SL. Avaliação de amarrotamento por meio de processamento de imagem de tecidos 100% algodão em processos de lavagem e secagem doméstica. Dissertation or Thesis; 2017.
35. Liu H, Wang Y, Gong RH, et al. The relationships between washing parameters, fabric movement, and wrinkling in a top–loading washer. Textile Research Journal. 2018;88(12):1367–1376.
36. Dittenber DB, GangaRao HVS. Critical review of recent publications on use of natural composites in infrastructure. Compos Part A Appl Sci Manuf. 2012;43(8):1419–1429.
37. Morton WE, Hearle JWS. Physical properties of textile fibres. Woodhead Publishing Limited, CRC Press, The Textile Institute; 2008.
38. Yu X, Li Y, Ding X. Relationship between drying parameters and drying performance in domestic tumble dryers. Textile Research Journal. 2020;0(0):1–16.