Mathematical modelling of direct drive of card machine drum

doi:10.15406/jteft.2018.04.00166

Journal of

eISSN: 2574-8114

Textile Engineering & Fashion Technology

Mini Review Volume 4 Issue 6

Mathematical modelling of direct drive of card machine drum

Jerzy Zajaczkowski

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Lodz University of Technology, Poland

Correspondence: Jerzy Zajaczkowski, Lodz University of Technology, 116 Zeromskiego Street, 90-924 Lodz, Poland

Received: August 10, 2017 | Published: November 19, 2018

Citation: Zajaczkowski J. Mathematical modelling of direct drive of card machine drum. J Textile Eng Fashion Technol. 2018;4(6):364-366. DOI: 10.15406/jteft.2018.04.00166

Download PDF

Abstract

The paper is concerned with the mathematical modelling of a directly driven card machine drum. The equations of the motion are derived taking account of an interaction of a drum and the electric motor.

Introduction

The problem of vibration of cylindrical shells is technically important. The equations of the motion can be found in works.^1–6 The natural vibrations have been studied in papers.^7–9 The vibrations of rotating shells have been investigated in papers.^10,11The phenomena of bifurcation and chaos in externally excited circular cylindrical shells have been reported in work.¹² The stress and transverse deflection of a card machine drum, in a form of a cylindrical shell with wound wire, have been calculated in.¹³ The purpose of this work is to formulate a mathematical model of a direct drive of a card machine drum.

Equations of the motion

The rotating shell of mean radius r is shown in Figure 1. Here, m denotes unit mass, g - gravity acceleration and t - time. The rotation angle of shell is denoted as α, the longitudinal and the angular co-ordinates of shell elements are denoted as x and φ. The longitudinal, circumferential and radial components of the shell surface deflection are denoted as u, v and w respectively.

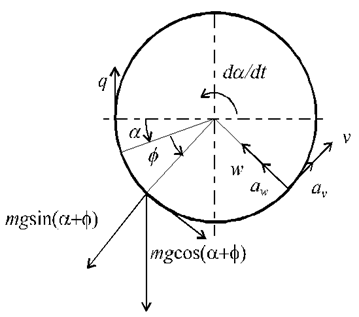
Figure 1 The rotating shell.

The components of the acceleration of the shell element have the form

$a_{v} = \frac{\partial^{2} v}{\partial t^{2}} - 2 \frac{d α}{d t} \frac{\partial w}{\partial t} + \frac{d^{2} α}{d t^{2}} (r - w) - {(\frac{d α}{d t})}^{2} v$ $a_{v} = \frac{\partial^{2} v}{\partial t^{2}} - 2 \frac{d α}{d t} \frac{\partial w}{\partial t} + \frac{d^{2} α}{d t^{2}} (r - w) - {(\frac{d α}{d t})}^{2} v$

$a_{w} = \frac{\partial^{2} w}{\partial t^{2}} + 2 \frac{d α}{d t} \frac{\partial v}{\partial t} + \frac{d^{2} α}{d t^{2}} v + {(\frac{d α}{d t})}^{2} (r - w)$ $a_{w} = \frac{\partial^{2} w}{\partial t^{2}} + 2 \frac{d α}{d t} \frac{\partial v}{\partial t} + \frac{d^{2} α}{d t^{2}} v + {(\frac{d α}{d t})}^{2} (r - w)$ (1)

Taking into account the inertia, damping and gravity forces, the loading of an element can be written as

$q_{x} = - c_{1} \frac{\partial u}{\partial t} - m \frac{\partial^{2} u}{\partial t^{2}}$ $q_{x} = - c_{1} \frac{\partial u}{\partial t} - m \frac{\partial^{2} u}{\partial t^{2}}$

$q_{ϕ} = - c_{2} \frac{\partial v}{\partial t} - m (\frac{\partial^{2} v}{\partial t^{2}} - 2 \frac{d α}{d t} \frac{\partial w}{\partial t} + \frac{d^{2} α}{d t^{2}} (r - w) - {(\frac{d α}{d t})}^{2} v) + m g cos (α + ϕ) - q_{s} δ (- α)$ $q_{ϕ} = - c_{2} \frac{\partial v}{\partial t} - m (\frac{\partial^{2} v}{\partial t^{2}} - 2 \frac{d α}{d t} \frac{\partial w}{\partial t} + \frac{d^{2} α}{d t^{2}} (r - w) - {(\frac{d α}{d t})}^{2} v) + m g \cos (α + ϕ) - q_{s} δ (- α)$
$q_{z} = - c_{3} \frac{\partial w}{\partial t} - m (\frac{\partial^{2} w}{\partial t^{2}} + 2 \frac{d α}{d t} \frac{\partial v}{\partial t} + \frac{d^{2} α}{d t^{2}} v + {(\frac{d α}{d t})}^{2} (r - w)) - m g sin (α + ϕ) + q_{n} δ (- α)$ $q_{z} = - c_{3} \frac{\partial w}{\partial t} - m (\frac{\partial^{2} w}{\partial t^{2}} + 2 \frac{d α}{d t} \frac{\partial v}{\partial t} + \frac{d^{2} α}{d t^{2}} v + {(\frac{d α}{d t})}^{2} (r - w)) - m g \sin (α + ϕ) + q_{n} δ (- α)$ (2)

Here, (c1, c1, c1) are coefficients of damping. The internal forces are assumed to be of the form

$N_{ϕ}^{'} = m {(\frac{d α}{d t})}^{2} r^{2}$
$N_{x}^{'} = N_{x^{1}} + N_{x^{2}} \cos ϕ$

$N_{x ϕ}^{'} = 0$ (3)

The internal torque is

$M_{s} (x) = m \int_{0}^{x} \int_{0}^{2 π} (\frac{\partial^{2} v}{\partial t^{2}} - 2 \frac{d α}{d t} \frac{\partial w}{\partial t} + \frac{d^{2} α}{d t^{2}} (r - w) - {(\frac{d α}{d t})}^{2} v) (r - w) r d ϕ d x$ (4)

The integration over entire length L of the shell gives the driving torque Ms. The angular acceleration is found as

$\frac{d^{2} α}{d t^{2}} = \frac{\frac{M_{s}}{m r} - \int_{0}^{L} \int_{0}^{2 π} ((\frac{\partial^{2} v}{\partial t^{2}} - 2 \frac{d α}{d t} \frac{\partial w}{\partial t} - {(\frac{d α}{d t})}^{2} v) (r - w)) d ϕ d x}{\int_{0}^{x} \int_{0}^{2 π} {(r - w)}^{2} d ϕ d x}$ (5)

The components of the shell surface deflection can be expressed in the form

$u (x . ϕ, t) = U T_{u}, v (x . ϕ, t) = V T_{v}, w (x . ϕ, t) = W T_{w}$ (6)

Where

$T_{u} = [\begin{matrix} T_{u n}^{(0)} (t) \\ T_{u n}^{(C N)} (t) \\ T_{u n}^{(S N)} (t) \end{matrix}], T_{v} = [\begin{matrix} T_{v n}^{(0)} (t) \\ T_{v n}^{(S N)} (t) \\ T_{v n}^{(C N)} (t) \end{matrix}], T_{w} = [\begin{matrix} T_{w n}^{(0)} (t) \\ T_{w n}^{(C N)} (t) \\ T_{w n}^{(S N)} (t) \end{matrix}],$ (7)

$\begin{array}{l} U = [U_{n}^{(0)} (x), U_{n}^{(C N)} (x) \cos N ϕ, U_{n}^{(S N)} (x) \sin N ϕ], \\ V = [V_{n}^{(0)} (x), V_{n}^{(S N)} (x) \sin N ϕ, V_{n}^{(C N)} (x) \cos N ϕ], \\ W = [W_{n}^{(0)} (x), W_{n}^{(C N)} (x) \cos N ϕ, W_{n}^{(S N)} (x) \sin N ϕ], \end{array}$ (8)

$\begin{array}{l} U_{n} (x) = [U_{1} (x), U_{2} (x), . . ., U_{n} (x)], \\ V_{n} (x) = [V_{1} (x), V_{2} (x), . . ., V_{n} (x)], \\ W_{n} (x) = [W_{1} (x), W_{2} (x), . . ., W_{n} (x)], \end{array}$ (9)

For n=1,2,3,...nmax, N=1,2,3,...Nmax.

Substituting (6-9) into equation (5) and carrying out the integration (5), one obtains

$\frac{d^{2} α}{d t^{2}} = \frac{(\begin{matrix} \frac{M_{s}}{m r} - \bar{V} \frac{d^{2} T_{v}}{d t^{2}} r + 2 \frac{d α}{d t} \bar{W} \frac{d T_{w}}{d t} r + {(\frac{d α}{d t})}^{2} \bar{V} T_{v} r \\ + 〈 \bar{V^{T} W}, \frac{d^{2} T_{v}}{d t^{2}} T_{w}^{T} 〉 - 2 \frac{d α}{d t} 〈 \bar{W^{T} W}, \frac{d T_{w}}{d t} T_{w}^{T} 〉 - {(\frac{d α}{d t})}^{2} 〈 \bar{V^{T} W}, T_{v} T_{w}^{T} 〉 \end{matrix})}{2 π L r^{2} - 2 r \bar{W} T_{w} + 〈 \bar{W^{T} W}, T_{w} T_{w}^{T} 〉}$ ,

$\int_{0}^{L} \int_{0}^{2 π} () d ϕ d x = \bar{()}, 〈 A, B 〉 = \sum_{r}^{} \sum_{c}^{} A_{r c} B_{r c}$ .(10)

The partial differential equations governing the motion of shell element will now be replaced by ordinary differential equations using Ritz-Galerkin. Let’s pre-multiply those equations4,5 by the transposition of functions (8) and then integrate of the resultant expressions by parts with the use of the forces-displacement relationships and boundary conditions

$\int_{0}^{2 π} \int_{0}^{l} U^{T} (\frac{\partial N_{x}}{\partial x} + \frac{1}{a} \frac{\partial N_{ϕ x}}{\partial ϕ} - Q_{x} \frac{\partial^{2} w}{\partial x^{2}} - N_{x ϕ} \frac{\partial^{2} v}{\partial x^{2}}) d x d ϕ +$

$\int_{0}^{2 π} \int_{0}^{l} U^{T} (- \frac{Q_{ϕ}}{a} (\frac{\partial v}{\partial x} + \frac{\partial^{2} w}{\partial x \partial ϕ}) - \frac{N_{ϕ}}{a} (\frac{\partial^{2} v}{\partial x \partial ϕ} - \frac{\partial w}{\partial x}) + q_{x}) d x d ϕ = 0$ ,

$\int_{0}^{2 π} \int_{0}^{l} V^{T} (\frac{1}{a} \frac{\partial N_{ϕ}}{\partial ϕ} + \frac{\partial N_{x ϕ}}{\partial x} + N_{x} \frac{\partial^{2} v}{\partial x^{2}} - \frac{Q_{x}}{a} (\frac{\partial v}{\partial x} + \frac{\partial^{2} w}{\partial x \partial ϕ})) d x d ϕ +$

$+ \int_{0}^{2 π} \int_{0}^{l} V^{T} (\frac{N_{ϕ x}}{a} (\frac{\partial^{2} v}{\partial x \partial ϕ} - \frac{\partial w}{\partial x}) - \frac{Q_{ϕ}}{a} (1 + \frac{\partial v}{a \partial ϕ} + \frac{\partial^{2} w}{a \partial ϕ^{2}}) + q_{ϕ}) d x d ϕ = 0$ ,

$\int_{0}^{2 π} \int_{0}^{l} W^{T} (\frac{\partial Q_{x}}{\partial x} + \frac{1}{a} \frac{\partial Q_{ϕ}}{\partial ϕ} + \frac{\partial}{\partial x} (N_{x ϕ} (\frac{v}{a} + \frac{\partial w}{a \partial ϕ})) + \frac{\partial}{\partial x} (N_{x} \frac{\partial w}{\partial x})) d x d ϕ +$

$+ \int_{0}^{2 π} \int_{0}^{l} W^{T} (\frac{N_{ϕ}}{a} + \frac{\partial}{\partial ϕ} (\frac{N_{ϕ}}{a} (\frac{v}{a} + \frac{\partial w}{a \partial ϕ})) + \frac{\partial}{\partial ϕ} (\frac{N_{ϕ x}}{a} (\frac{\partial w}{\partial x})) + q_{z}) d x d ϕ = 0$ . (11)

As a result of the integration, we obtain a set of three ordinary differential equations of second order

$K_{11} T_{u} + K_{12} T_{v} + K_{13} T_{w} + K_{12}^{(1)} {(\frac{d α}{d t})}^{2} T_{v} + K_{13}^{(1)} {(\frac{d α}{d t})}^{2} T_{w} + C_{11} \frac{d T_{u}}{d t} + M_{11} \frac{d^{2} T_{u}}{d t^{2}} = F_{1}$ ,

$\begin{matrix} K_{21} T_{u} + K_{22} T_{v} + K_{23} T_{w} + K_{22}^{(1)} {(\frac{d α}{d t})}^{2} T_{v} + K_{23}^{(2)} \frac{d^{2} α}{d t^{2}} T_{w} + C_{23} \frac{d α}{d t} \frac{d T_{w}}{d t} + \\ + C_{22} \frac{d T {}_{v}}{d t} + M_{22} \frac{d^{2} T {}_{v}}{d t^{2}} + M_{24} \frac{d^{2} α}{d t^{2}} + F_{2 c} \cos α + F_{2 s} \sin α + F_{2} (α) = 0, \end{matrix}$

$\begin{array}{l} K_{31} T_{u} + K_{32} T_{v} + K_{33} T_{w} + K_{32}^{(1)} {(\frac{d α}{d t})}^{2} T_{v} + K_{33}^{(1)} {(\frac{d α}{d t})}^{2} T_{w} + K_{32}^{(2)} \frac{d^{2} α}{d t^{2}} T_{v} + \\ + C_{32} \frac{d α}{d t} \frac{d T_{v}}{d t} + C_{33} \frac{d T_{w}}{d t} + M_{33} \frac{d^{2} T_{w}}{d t^{2}} + F_{3 c} \cos α + F_{3 s} \sin α + F_{3} (α) = 0. \end{array}$ (12)

Introducing matrices of three times higher order, than the matrices in equations (12), these set can be rewritten as one equation

$M \frac{d^{2} T}{d t^{2}} + C \frac{d T}{d t} + K T + {(\frac{d α}{d t})}^{2} K^{(1)} T + \frac{d^{2} α}{d t^{2}} K^{(2)} T + C^{(1)} \frac{d α}{d t} \frac{d T}{d t} + F_{c} \cos α + F_{s} \sin α + F (α) = 0$ (13)

Where T=[Tu,Tv,Tw].

Adding now equation governing the driving torque of the motor

$\frac{d M_{s}}{d t} = \frac{1}{T_{s}} (C_{s} (Ω_{s} - \frac{d α}{d t}) - M_{s})$ (14)

We obtained the set of three equations (10,13,14) from which angle of drum rotation α, components of elastic deflection T (7-9)and driving torque Ms can be found through numerical integration. Similar calculations were performed by the author for a spindle directly driven by three-phase electric motor.¹⁴