In this paper, the solving the original specific problem of optimal control is described. Designing optimal algorithm of controlling a spacecraft motion increases efficiency of onboard control system of a spacecraft and originates more economical performance of spacecraft during flight on orbit. Analytic solution of the proposed problem is presented for case when a required time interval of control is known, and rotation energy functional should be minimized. The quaternion method and maximum principle are used. For dynamically symmetric spacecraft, complete solution of spacecraft reorientation problem in closed form is given. If the controlling torque is limited, analytical formulas were written for duration of acceleration and braking. It is shown that chosen criterion of optimality provides a turn of a spacecraft with minimal rotation energy at fixed time. Example and mathematical simulation results for spacecraft motion under optimal control are given.

Keywords: spacecraft attitude, quaternion, optimal control, maximum principle

The problem of bringing a spacecraft into target orientation position is solved. The solution method and the formalized description of spacecraft’s rotational motion kinematics are based on the method of quaternions.¹ Spatial reorientation is a transferring the fixed axes of spacecraft’s hull from one known attitude into another given angular position in finite time T. Angular orientation of the body-fixed coordinate system is defined relative to the chosen reference basis I. An often encountered case, when reference system is inertial coordinate system, is considered.

Numerous works have been dedicated to studying the controlled rotations of rigid body and optimal control problem for spacecraft reorientation in various statements.^1-25 In particular, the solution was constructed for special case when the spacecraft rotates around a finite rotation vector.² The rotation maneuvers around the principal central axe of spacecraft’s inertia ellipsoid were studied in detail.⁴ Notice, many publications describe solutions when rigid body rotates around the Euler axis,^1-5 although optimization principles and control algorithms differ including use of quaternions,¹ fuzzy logic² and the method of inverse dynamic problem.^4,5 At the same time, a turn in the least turn-angle plane is not optimal in many practical cases, no matter how exactly it is executed. Also, time-optimal maneuvers is interesting and topical, therefore they are popular.^{4, 6-12} Many authors have noted that an analytical solution to the optimal turn problem in a closed form, if it were found, would be of great practical interest, since it allows the finished laws of programmed control and modification of the optimal trajectory of spacecraft motion to be applied onboard the spacecraft.^7,8 Certain solutions are known for an axially symmetric spacecraft.^12-14 However, an analytical solution to the three-dimensional  turn problem of the spacecraft with arbitrary mass distribution with arbitrary boundary conditions for spacecraft’s angular position has not been found; only certain particular cases are known when the problem of a turn has been solved (e.g.,.^1,7,10 Therefore, in the general case, we are forced to rely only on the approximate numerical solution to the problem. In some cases (e.g.,⁶), authors faced difficulties, related to the in homogeneity of the optimal control function, in an attempt to find numerical solutions to the optimization boundary-value problems for spacecraft’s optimal turn problems (it is typical for time-optimal problems). The numerical solution of optimal turn problem for dynamically symmetric spacecraft is considered in detail,¹³ where authors solved the maximum-principle boundary-value problem by replacing the variables and reducing it to the boundary-value problem of a turn of a spherically symmetric body. Also, special control regime of spacecraft rotation was studied in the problem of optimal reorientation.¹⁴ Attitude control of the spacecrafts with inertial actuators (or gyrodins) has specific features.^15–18 For control system of the spacecrafts, controlled by inertial actuators, the patented method¹⁹ can be used.

In this paper, index of optimality characterizes energy consumption for spacecraft reorientation. Issues of cost-efficiency also remain relevant for the time being for spacecraft motion control. Its minimization remains a very important problem in practice of spacecraft flight. Finding and studying the optimal attitude control problem for spacecraft reorientation from one spatial position into another (with respect to rotation energy) is topic and subject of this research.

The main results of research work are the following: the carried out research has reached an overall objective since optimal control program of spacecraft reorientation with minimal rotation energy within given time interval was found; it was demonstrated that two-impulse control when spacecraft rotates by inertia between acceleration and braking is optimum; for optimal solution, estimations of the relative growth in the functional of quality due to the limited controlling moment were done.

Angular motion of the spacecraft as rigid body is described by dynamic Euler equations³

$J_1{\dot{\omega }}_1+\left(J_3-J_2\right){\omega }_2{\omega }_3=M_1$ ,$J_2{\dot{\omega }}_2+\left(J_1-J_3\right){\omega }_1{\omega }_3=M_2$ ,$J_3{\dot{\omega }}_3+\left(J_2-J_1\right){\omega }_1{\omega }_2=M_3$ (1)

where J_i  are the spacecraft’s principal central moments of inertia, M_i are projections of the main moment M of the forces onto the principal central axes of the spacecraft’s inertia ellipsoid, ${\omega }_i$ are projections of the spacecraft’s absolute angular velocity vector  onto the axes of the body-fixed basis E formed by the principal central axes of spacecraft’s inertia ellipsoid (i=$\overline{1,3}$ ). To describe the spacecraft’s spatial motion, the mathematical apparatus of quaternions (Euler–Rodrigues parameters) is used. Motion of the body-fixed basis E relative to the reference basis I will be given by a quaternion $\Lambda$ .¹The angular positions of the initial and final spacecraft attitude with respect to the reference basis I are given by quaternion’s ${\Lambda }_{\text{in}}$ and ${\Lambda }_{\text{f}}$ , respectively. Without loss of generality, it is assumed that basis I is inertial. In this case, the following kinematic equations hold:

$2{\dot{\lambda }}_0=-{\lambda }_1{\omega }_1-{\lambda }_2{\omega }_2-{\lambda }_3{\omega }_3$ ,$2{\dot{\lambda }}_1={\lambda }_0{\omega }_1+{\lambda }_2{\omega }_3-{\lambda }_3{\omega }_2$ ;(2)

$2{\dot{\lambda }}_2={\lambda }_0{\omega }_2+{\lambda }_3{\omega }_1-{\lambda }_1{\omega }_3$ ,$2{\dot{\lambda }}_3={\lambda }_0{\omega }_3+{\lambda }_1{\omega }_2-{\lambda }_2{\omega }_1$

Where ${\lambda }_j$ are components of quaternion  (j=$\overline{0,3}$ ).¹ For simplicity, the quaternion $\Lambda$ specifying the current spacecraft orientation is assumed the normalized quaternion (||$\Lambda$ ||= 1).

In space flight, an important characteristic feature of spacecraft motion control is that the disturbing moments caused by the vehicle’s interaction with external fields and environmental resistance are small. The spacecraft motion control relative to its center of mass is done by changing the moment of forces M (external or internal, if spacecraft orientation control is done with inertial actuators, i.e., powered gyroscopes). The boundary conditions are written as:

$\Lambda (0)={\Lambda }_{\text{in}}$ (3)

$\Lambda (T)={\Lambda }_{\text{f}}$ (4)

where T is the time of ending the reorientation process, and the quaternion’s${\Lambda }_{\text{in}}$ and ${\Lambda }_{\text{f}}$ determining the orientation of spacecraft fixed axes at the initial and final time instants have arbitrary predefined values satisfying the condition ||${\Lambda }_{\text{in}}$ ||=||${\Lambda }_{\text{f}}$ ||=1. For optimization of reorientation control, quadratic criterion of quality is used.²⁵ The coefficients of the functional of quadratic criterion of quality was chosen in that way, at which efficiency of the control is estimated by the integral value

$G={\displaystyle \underset{0}{\overset{T}{\int }}(J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2)dt}$ (5)

The reorientation optimal control problem is formulated as follows: spacecraft must transfer from position (3) into position (4) according to equations (2) with minimal value of the functional (5). The equations (1) are necessary for determining the moments M_i during optimal rotation, after solving this control problem (2)-(5). The index (5) is the integral of the kinetic rotation energy on the given time interval. The time T when the spacecraft reorientation maneuver should end is fixed. The assumed optimality criterion allows for estimation of an energetically advantageous angular motion trajectory along which the spacecraft will turn from its initial position ${\Lambda }_{\text{in}}$ into the required final angular position ${\Lambda }_{\text{f}}$ , and for finding the corresponding control mode. Also, the chosen criterion of optimality provides turn of a spacecraft with minimal rotation energy at fixed time.

The proposed problem of optimal control is the classical kinematic rotation problem.¹ To find the motion law (t) optimal with respect to criterion (5), it is assumed that the time of ending the reorientation maneuver T is given. The value of the optimality functional (5) does not explicitly depend on the moment M of controlling (expression (5) does not contain M_i). It is considered, angular velocity projections ${\omega }_i$  are control variables, and compute moments M_i by substituting the found optimal functions ${\omega }_i$ (t) into equations (1) (i=$\overline{1,3}$ ). The form of functional (5) is special case of typical (relatively standard) form of the optimized functional²⁵ (if take into account the fact that the spacecraft angular velocity vector $\omega$ is the control variables). The restriction for phase variables ${\lambda }_j$ is insignificant because it is always satisfied (for any possible spacecraft motion around its center of mass). Variables ${\lambda }_j$ (being the components of quaternion Λ) have a characteristic feature: due to equations (2), the norm ||Λ|| of the quaternion Λ is constant, ||Λ||=const.¹ 

For solving the posed problem, the Pontryagin’s maximum principle is used.²⁶ Since the minimized functional (5) does not depend on position coordinates ${\lambda }_j$ the universal variables r_i proposed earlier can be used (i=$\overline{1,3}$ ),²⁰ and to introduce the conjugate variables corresponding to the phase variables is not obligatory. The Hamiltonian H of problem (2)-(5) looks like the following:

$H={\omega }_1{r}_1+{\omega }_2{r}_2+{\omega }_3{r}_3-J_1{\omega }_1^2-J_2{\omega }_2^2-J_3{\omega }_3^2$ (6)

Where the functions r_i are²⁰

$r_1=({\lambda }_0{\psi }_1+{\lambda }_3{\psi }_2-{\lambda }_1{\psi }_0-{\lambda }_2{\psi }_3)/2$

$r_2=({\lambda }_0{\psi }_2+{\lambda }_1{\psi }_3-{\lambda }_2{\psi }_0-{\lambda }_3{\psi }_1)/2$

$r_3=({\lambda }_0{\psi }_3+{\lambda }_2{\psi }_1-{\lambda }_3{\psi }_0-{\lambda }_1{\psi }_2)/2$

${\psi }_j$ are the conjugate variables corresponding to components of quaternion ${\lambda }_j$ (j=$\overline{1,3}$ ).

The first terms (it contains the universal variables r_i ) comprise the kinematical part of the Hamiltonian H which is responsible for the geometric properties of optimal motion. The other terms (it contains the spacecraft’s moments of inertia) corresponds to the chosen optimality criterion. The function H does not take into account the phase constraint ||Λ||=1, since ||Λ(0)||= 1. For the universal variables r_i , the following system of equations are true²⁰:

${\dot{r}}_1={\omega }_3{r}_2-{\omega }_2{r}_3$ , ${\dot{r}}_2={\omega }_1{r}_3-{\omega }_3{r}_1$ ,${\dot{r}}_3={\omega }_2{r}_1-{\omega }_1{r}_2$ (7)

The change in vector r formed by the universal variables r_i is given by the solution of the following equation $\dot{r}=-\omega \times r$

(it is vector form of the equations (7) if variables r_i assume projections of vector r on the axes of the body-fixed basis E.²⁰ The symbol×denotes the vector product of two vectors. As it is know, the vector r turns out to be motionless relative to the inertial basis I, and |r|=const¹0.²⁰ Thus, the problem of finding an optimal control reduces to solving the system of equations of spacecraft’s angular motion (2) and equations (7) under the condition that the control itself is chosen by maximizing the Hamiltonian. The system of equations (7) which determines the behavior of vector r relative to fixed axes replaces the conjugate system of equations. The optimal vector function r(t) is related with attitude quaternion Λ(t) by the formula

$r=\tilde{\Lambda }\circ c_E\circ \Lambda$ , where$c_E={\Lambda }_{\text{in}}\circ r(0)\circ {\tilde{\Lambda }}_{\text{in}}=const$

The direction of vector c_E depends on the initial and final spacecraft positions. In order, for the spacecraft to have the required orientation at the right end $\Lambda (T)={\Lambda }_{\text{f}}$ , the vector c_E (or the value of vector r at the initial moment) by the corresponding solutions of system (2) should be determined. The system of differential equations (7), together with the maximality condition of the Hamiltonian H, is necessary conditions of optimality. Constraint equations are given by the system of equations (2) which describes the spacecraft’s motion relative to its center of mass. The maximum conditions of function H determine sought solution (t). Boundary position conditions Λ(0) and Λ(T) determine solutions Λ(t) and r(t). The boundary problem of the maximum principle is to find the value of the vector r(0) for which the solution of the system of differential equations (2),(7) together with simultaneous maximization, at every current moment of time, of the Hamiltonian H satisfies reorientation conditions (3), (4) (the restriction on phase variables ${\lambda }_j$ is not taken into account since the equality ||Λ(t)||=1 always holds due to equations (2)).

To find the control function ($\omega$ t) (the optimal control problem) and the optimal vector r, the conditions of maximum for Hamiltonian H must be formalized. From formula (6) follows, Н is a concave quadratic function of the angular velocity $\omega$ , and hence its maximal value is achieved at the point of the local extremum. Applying the necessary conditions $\partial H/\partial {\omega }_i=0$ , the equations $r_i-2J_i{\omega }_i=0$ is obtained. The function Н is maximal if the relations

${\omega }_i=r_i/2J_i$ (8)

are satisfied. The problem of constructing an optimal control has been reduced to solving the system of equations of spacecraft’s angular motion (2) and equations (7) under the condition that control function is formed from requirement (8). The formulated control problem (2)–(5) is solved completely.

Due to the fact that |r|=const=|r(0)|¹0, for simplicity, to the normalized vector p=r/|r| is used, |p|=1. For the vector p, it holds that,$\dot{p}=-\omega \times p$ or

${\dot{p}}_1={\omega }_3{p}_2-{\omega }_2{p}_3$ , ${\dot{p}}_2={\omega }_1{p}_3-{\omega }_3{p}_1$ , ${\dot{p}}_3={\omega }_2{p}_1-{\omega }_1{p}_2$ (9)

In what follows, the components p_i of the vector p will be used. Note that r_i=|r(0)|p_i. The necessary condition of optimality can be written as

$J_i{\omega }_i=b.p_i$ (10)

where b>0 is a scalar value.

Left-hand sides of equations (10) are projections of the spacecraft’s angular momentum vector onto the body-fixed basis axes E. Expressions (10) lead to the conclusion that spacecraft rotation during optimal motion is done with a constant direction of angular momentum relative to the inertial coordinate system. The value of b equals the modulus of the spacecraft’s angular momentum L. The triple p₁, p₂, p₃ represents directional cosines of the vector L relative to the body-fixed basis axes E. Equations (10) clearly show that in the geometric representation, the vector p is simply the unit vector of the spacecraft’s angular momentum vector L in the spacecraft’s fixed system of coordinates. Thus, the optimal (in the sense of minimizing the energy integral) spacecraft reorientation is performed along the “trajectory of free motion”. Equations (9), together with equalities (10), form a closed system of equations which determine unique properties of optimal motion. Original solution is determined by close this system of equations (9), (10) by equations (2) with conditions (3), (4) for solution Λ(t).

Here and in what follows, it is assumed that the “trajectory of free motion” is a family (totality or multitude) of angular positions (values of Λ) that a rigid body occupies during its rotation by inertia. In the geometric interpretation, the “trajectory of free motion” is a trace of the representing point Λ(t), where Λ(t) is a solution of the system of differential equations (1), (2) when M₁=M₂=M₃=0 and ${\omega }_i$ ≠0. Moreover, it is known that the end of the angular velocity vector $\omega$ (t) during the free motion of rigid body moves along a centroid. ^27,28

Let us find the proportion between the kinetic energy E_k and angular momentum L during optimal slew maneuver. The kinetic energy E_k and the value b are related by expression

$E_k=b^2(p_1^2/J_1+p_2^2/J_2+p_3^2/J_3)/2$

Therefore, the proportion.$E_k/{\left|L\right|}^2=(p_1^2/J_1+p_2^2/J_2+p_3^2/J_3)/2$

It is shown that this proportion E_k/|L|² is constant on the entire motion interval 0≤t≤T. The Hamiltonian H is independent of time in explicit form, i.e. . Therefore, H=const inside the entire interval of control 0≤t≤T.²⁷ From formulas (6), the equality

${\omega }_1{r}_1+{\omega }_2{r}_2+{\omega }_3{r}_3-J_1{\omega }_1^2-J_2{\omega }_2^2-J_3{\omega }_3^2=\text{const}$

is obtained. After substitution the values ${\omega }_i$ calculated by equations (8) in this equality, the conditions

$r_1^2/J_1+r_2^2/J_2+r_3^2/J_3=\text{const}$ , and$p_1^2/J_1+p_2^2/J_2+p_3^2/J_3=\text{const}$

are satisfied because |r| =const. Therefore, $E_k/{\left|L\right|}^2=const$ . It is key property of optimal motion for criterion (5).

Thus, the problem of constructing the optimal control (t) has been mainly reduced to finding such a value of vector p(0) that as a result of the spacecraft’s motion, according to equations (2), (9), and (10), the equality (4) will satisfy. It is virtually impossible to find a general solution of this system of equations. The problem is to find boundary conditions on p(0) and p(T) which are related by expression

${\Lambda }_{\text{f}}\circ p(T)\circ {\tilde{\Lambda }}_{\text{f}}={\Lambda }_{\text{in}}\circ p(0)\circ {\tilde{\Lambda }}_{\text{in}}$ (11)

The property |L|=const follows from relations (8) which reflect the Hamiltonian H maximizing property. It is demonstrated above, proportion E_k/|L|² is constant, so E_k=const during optimal rotation. An exact value of the kinetic energy E_k and modulus of angular momentum are determined by the end time of the reorientation maneuver T (by the condition that as a result of solving the system (2), (9), (10), the boundary condition (4) is satisfied at the right end). The found modulus |L| will correspond to the minimal possible spacecraft’s kinetic rotation energy E_k that provides for reaching the final position ${\Lambda }_{\text{f}}$ in allotted time T. Note, the vectors $\omega$ and p are related as

${\omega }_i=\frac{\sqrt{2E_k}}{\sqrt{p_1^2/J_1+p_2^2/J_2+p_3^2/J_3}}\cdot \frac{p_i}{J_i}$ (12)

Let us now find the controlling moments necessary to support the spacecraft’s optimal rotation mode in time interval 0<t<T during the reorientation. Let us substitute the functions ${\omega }_i$ (t) computed by expressions (8) into dynamic equations (1) with taking into account the fact |r| =const. As result, all component of moment M are M_i=0. In the solution optimal with respect to criterion (5), the spacecraft’s reorientation is done with zero controlling moment M=0. This follows from the analysis of equations (8) that show a relation between the angular momentum L and the vector r of universal variables. The fact that L=r/2 and |L|=const, keeping in mind the immobility of vector r in the inertial basis I, implies that the spacecraft’s angular momentum vector is constant relative to inertial coordinate system during the reorientation. The kinetic energy E_k is constant also.Thus, it is proven the following conclusion: spacecraft’s reorientation occurs with the minimal value of the kinetic energy integral if and only if the spacecraft during this reorientation rotates as a free motion (the main moment of forces is zero), i.e., when the spacecraft’s rotation (as a rigid body) is an Euler–Poinsot motion.²⁸ If allow a step like change of the angular velocity vector $\omega$ , then the proposed optimal control problem (the kinematic reorientation problem) can be considered solved: Equations (2), (9), and (12) completely define the necessary motion $\omega$ (t).

The task of the onboard control system for realization of optimal control is to inform the spacecraft of the initial motion conditions, namely the calculated angular velocity at time moment t=0 and reducing the kinetic energy to zero at time moment t=T, when $\Lambda (t)={\Lambda }_{\text{f}}$ (after the spacecraft reaches its final position ${\Lambda }_{\text{f}}$ ). From the moment of reaching the necessary initial angular velocity and until the reorientation is finished, when the spacecraft will be in the neighborhood of the required position ${\Lambda }_{\text{f}}$ , there is no torque M acting on the spacecraft’s body; the spacecraft performs uncontrolled rotation (M=0), i.e. free motion. Creating the initial angular velocity and damping the final rotation happens in an impulse (as fast as the spacecraft’s actuators will allow). Between the impulsive imparting of angular momentum and the impulsive suppressing of angular momentum

$J_1^2{\omega }_1^2+J_2^2{\omega }_2^2+J_3^2{\omega }_3^2=\text{const}$ , $J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2=\text{const}$ (13)

Topicality of the considered problem is due to the fact that by minimizing integral (5) the energy spent to perform spacecraft reorientation from position ${\Lambda }_{\text{in}}$ into position in ${\Lambda }_{\text{f}}$ time T is minimized. The energy E obeys the following relation:

$T\underset{0\le t\le T}{\max }E\ge {\displaystyle \underset{0}{\overset{T}{\int }}(J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2)dt}/2$

Consequently, minimum of quantity $\underset{0\le t\le T}{\max }E$ is

$\underset{0\le t\le T}{\max }E={\displaystyle \underset{0}{\overset{T}{\int }}(J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2)dt}/2T$

The minimal value of energy, required for spacecraft rotation satisfying given boundary conditions (3), (4), is reached in the only one case when $J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2=\text{const}$ and the integral (5) is minimum. Both last conditions satisfy for motion under the equations (7), (8) which are the necessary conditions of optimality (see (13) also). As a result, when the functional (5) is minimized, we actually arrive at the minimum rotary energy $\underset{0\le t\le T}{\max }E$ and, as corollary; the minimum energy of the control forces is achieved. The spacecraft rotation regime according to conditions (7), (8) (or (9), (12)) gives the absolute minimum of the controlling forces’ work since in time interval 0<t<T the spacecraft rotates without control (with moment M=0).

Constructing the optimal reorientation regime with minimal value of integral (5) is non-trivial task. In the optimal reorientation problem (in constructing the optimal programmed motion $\omega$ (t)), it is crucial to find the initial vector p(0) and the corresponding angular velocity $\omega$ (0+) (the angular velocity (0+) is calculated by formulas (12)). The vector p(0) depends on reorientation parameters ${\Lambda }_{\text{t}}$ and the spacecraft characteristics J₁, J₂, J₃. For arbitrary values J₁¹J₂¹J₃ , it is hard to find the solution of the considered problem of spacecraft’s three-dimensional reorientation for arbitrary values ${\Lambda }_{\text{in}}$ and ${\Lambda }_{\text{f}}$ . The difficulty is to find boundary vectors p(0) and p(T) which are related by (11). Analytical solution of the system of equations (2), (9), and (12) exists for dynamically spherical and dynamically symmetric bodies only. For a spherically symmetric spacecraft (when J₁=J₂=J₃), the solution p(t), $\omega$ (t) have elementary form: p(t)=const and $\omega$ (t)=const, or in detail

$p_i={\nu }_i/\sqrt{{\nu }_1+{\nu }_2+{\nu }_3}$ , and${\omega }_i=\frac{2{\nu }_i{\arccos }_{}{\nu }_0}{T\sqrt{{\nu }_1+{\nu }_2+{\nu }_3}}$

Where ${\nu }_0,{\nu }_1,{\nu }_2,{\nu }_3$ are components of the reorientation quaternion.${\Lambda }_{\text{t}}={\tilde{\Lambda }}_{\text{in}}\circ {\Lambda }_{\text{f}}$

For a dynamically symmetric spacecraft (for example, when J₂=J₃), the optimal control problem can be solved completely also. For this distribution of spacecraft’s mass, the following differential equations:

$J_2{\dot{\omega }}_2=\left(J_3-J_1\right){\omega }_1{\omega }_3$ ,$J_3{\dot{\omega }}_3=\left(J_1-J_2\right){\omega }_1{\omega }_2$

are satisfied under condition ${\omega }_1=\text{const}$ .

Last system of differential equations describes the oscillator (with the parameter ${\omega }_1=\text{const}$ ), for which ${\omega }_2$ and ${\omega }_3$ are harmonic functions of time. Therefore, р₁=const=р₁₀ and harmonic oscillations of the functions р₂ and р₃ are observed. In this special case, the optimal motion is the simultaneous rotation of the spacecraft as a rigid body around its axial axis OX and around spacecraft’s angular momentum L which is constant in the inertial space and which constitutes a certain constant angle $\vartheta$ with the spacecraft’s axial axis. Angular velocities with respect to OX and p axes have a constant ratio (as is shown above, vectors L and p are parallel). The solution of system (2), (9), (12), necessary for solving the control problem, is regular precession. For the regular precession case

${\Lambda }_{\text{f}}={\Lambda }_{\text{in}}\circ {е}^{p_{\text{o}}\beta /2}\circ e^{e_{\text{1}}\alpha /2}$

where p₀=p(0); e₁ is the unit vector of the spacecraft’s axial axis; is the spacecraft’s rotation angle around its axial axis; $\beta$ is the spacecraft’s rotation angles around the vector p, e is quaternion exponent.¹ It is assumed that |α|≤Π, 0≤β≤Π.

For a dynamically symmetric spacecraft with moments of inertia $J_1\ne J_2=J_3$ , the solution p(t) is written as follows:

$p_1=p_{10}=\text{const}=\cos \vartheta$ , $p_2=p_{20}\cos \kappa +p_{30}\sin \kappa$ , $p_3=-p_{20}\sin \kappa +p_{30}\cos \kappa$ (14)

where

$\kappa =\frac{J_3-J_1}{J_2}{\displaystyle \underset{0}{\overset{t}{\int }}{\omega }_1(t)dt}.$

In this case, dependences (14), together with equalities (12), form a solution of the system of equations (2), (9) under condition (10). At the same time, the vector p also generates a cone around the axial axis OX in the body-fixed coordinate system. The specific value of р₀ is determined exclusively by the requirement that, according to equations (2),(9), (12), boundary conditions (3) and (4) be satisfied. In this type of control, the spacecraft’s angular momentum preserves a constant direction in the inertial reference basis I, while the axially symmetric body moves along a “conic trajectory”. To move the spacecraft from position ${\Lambda }_{\text{in}}$ into position ${\Lambda }_{\text{f}}$ , it rotates simultaneously around the vector c_E, which is constant relative to the inertial basis I, by the angle β, and around its own longitudinal axis by the angle α. Using the mathematical formalism of quaternions to describe rotations of rigid body about the center of mass, relations reflecting a dependence between the values p₀, α,β and are written. The dependence of parameters p₀,α, and β on the boundary angular positions ${\Lambda }_{\text{in}}$ and ${\Lambda }_{\text{f}}$ is given by the following system of equations:

$\cos \frac{\beta }{2}\cos \frac{\alpha }{2}-p_{10}\sin \frac{\beta }{2}\sin \frac{\alpha }{2}={\nu }_0$ , $p_{20}\sin \frac{\beta }{2}\cos \frac{\alpha }{2}+p_{30}\sin \frac{\beta }{2}\sin \frac{\alpha }{2}={\nu }_2$ , $\cos \frac{\beta }{2}\sin \frac{\alpha }{2}+p_{10}\sin \frac{\beta }{2}\cos \frac{\alpha }{2}={\nu }_1$ , $-{р}_{20}\sin \frac{\beta }{2}\cos \frac{\alpha }{2}+p_{30}\sin \frac{\beta }{2}\cos \frac{\alpha }{2}={\nu }_3$ , $\alpha =\frac{J_2-J_1}{J_1}{p}_{10}\beta$

For a given reorientation time T, angular rotation speeds around the OX and p axes are equal to $\dot{\alpha }=\alpha /T$ ,and $\dot{\beta }=\beta /T$ . The magnitude of angular momentum during optimal rotation is |L|=J₂β/T. The programmed values of controlling functions ${\omega }_i$ (projections of the angular velocity vector $\omega$ ) have the following form:

${\omega }_1=\dot{\alpha }+\dot{\beta }{p}_{10}$ ,${\omega }_2=\dot{\beta }\sqrt{1-p_{10}^2}\sin (\dot{\alpha }t+{\sigma }_0)$ ,${\omega }_3=\dot{\beta }\sqrt{1-p_{10}^2}\cos (\dot{\alpha }t+{\sigma }_0)$

where ${\sigma }_0={\text{arctg}}_{}(p_{20}/p_{30})$ .

Notice, optimal values p₀, α, and β corresponding to solution of last system of five transcendent equations and which correspond to free motion from position ${\Lambda }_{\text{in}}$ into position ${\Lambda }_{\text{f}}$ can be determined with using the device.²⁹ For a non-symmetric spacecraft (when J₁=J₂=J₃), the system (2), (9),(12) can be solved by numerical methods only (e.g., using the method of successive approximations or iterations methods with consecutive approach to true solution). To find the vector p₀, it is necessary the solving the boundary problem $\Lambda (0)={\Lambda }_{\text{in}}$ ,$\Lambda (T)={\Lambda }_{\text{f}}$ , taking into account the equations (1), (2) imposed upon the motion, in which M_i=0. As a result, the value of the angular velocity vector at the initial time moment ${\omega }_{\text{cal}}$ , for which the spacecraft is moved with its free rotation with respect to the center of mass (M=0) from the state $\Lambda (0)={\Lambda }_{\text{in}}$ , $\omega$ (0)=${\omega }_{\text{cal}}$ to the state $\Lambda (T)={\Lambda }_{\text{f}}$ , will be found ($\omega$ (T) is arbitrary here). In particular, the method of solving the boundary problem and determining the vector p₀ was described in detail in article.¹¹ The value of vector p₀ relates to ${\omega }_{\text{cal}}$ as

${р}_{i0}=\frac{J_i{\omega }_{i\text{cal}}}{\sqrt{{\left(J_1{\omega }_{1\text{cal}}\right)}^2+{\left(J_2{\omega }_{2\text{cal}}\right)}^2+{\left(J_3{\omega }_{3\text{cal}}\right)}^2}}$

The known algorithms presented in patent²³ and system²⁴ can be used for finding calculated values ${\omega }_{\text{cal}}$ and p₀ also. These algorithms^11,23,24 are reliable and provide asymptotic approaching for sought value p₀. Other calculation schemes^30-32 can be useful only in some specific cases.

In many practical tasks, reorientation is made in situation when initial state satisfies condition ω(0)=0 and final angular velocity must be absent ω (T)=0 (these cases occur very frequently, especially if attitude control is done relative to inertial coordinate system). It is obvi ous, in instants of time t=0 and t=T, angular velocity calculated according to the formula (12), corresponding to nominal program of optimal rotation maneuver, is not equal to zero. Therefore, segments of acceleration and braking at the beginning and the ending of slew maneuver are inevitable. For the optimal motion, spacecraft reorientation from one angular position ${\Lambda }_{\text{in}}$ to another position ${\Lambda }_{\text{f}}$ is done by impulsive imparting the necessary angular velocity (the nominal value of the angular momentum vector) to the spacecraft, rotation of the spacecraft with constant kinetic energy and modulus of angular momentum, and short-term (impulse) reduction of the rotation energy to zero. Very important characteristic for reorientation maneuver is integral

$S={\displaystyle \underset{0}{\overset{Т}{\int }}\left|L(t)\right|dt}$ (15)

The value of characteristic S is determined only by the rotation conditions ${\Lambda }_{\text{in}}$ ,${\Lambda }_{\text{f}}$ , and the spacecraft’s principal central moments of inertia J₁, J₂, J₃. If time of reaching the calculated angular velocity which is equal

${\omega }_{i\text{ nom}}=\frac{\sqrt{2E_k}}{J_{i}C}{p}_{i0}$

and duration of suppressing the angular velocity to zero are infinitesimal, then modulus of angular momentum during uncontrolled motion (between acceleration and braking) is |L|=S/T, where integral (15) is calculated as

$S=t_{\text{pr}}\sqrt{J_1^2{\omega }_{1\text{cal}}^{\text{2}}+J_2^2{\omega }_{2\text{cal}}^{\text{2}}+J_3^2{\omega }_{3\text{cal}}^{\text{2}}}$

Where t_pr is the predicted time of achieving the condition $\Lambda (t_{\text{pr}})={\Lambda }_{\text{f}}$ during free rotation from the position $\Lambda (0)={\Lambda }_{\text{in}}$ with initial angular velocity ω(0)=${\omega }_{\text{cal}}$ (according to the equations (2), (1) in which all values M_i=0). Note, the value S and vector p₀, which satisfy optimal motion, are computed together. Denote

$C=\sqrt{p_{10}^2/J_1+p_{20}^2/J_2+p_{30}^2/J_3}$

For a spherically symmetric spacecraft and for a dynamically symmetric spacecraft, key characteristics and constants of control law are determined straightforwardly, without integration of motion equations (1), (2). For a spherically symmetric spacecraft, the integral S is calculated as

$S=2J_1\arccos {\nu }_{\text{0}}$

Accordingly, optimal modulus of angular momentum during uncontrolled rotation is

$L_{\text{opt}}=2J_1\arccos {\nu }_{\text{0}}/T$

and kinetic energy is

$E_k=2J_1{\arccos }^2{\nu }_{\text{0}}/T^2$

For an axially symmetric spacecraft (when J₂=J₃), the integral S is equal

$S=J_2\beta$

Optimal modulus of angular momentum during uncontrolled rotation is

$L_{\text{opt}}=J_2\beta /T$

and kinetic energy is

$E_k=J_2^2{\beta }^2({\cos }^2\vartheta /J_1+{\sin }^2\vartheta /J_2)/(2T^2)$

If the moment M is limited, some non-zero time is required for imparting the required angular momentum to the spacecraft and for suppressing the existing angular momentum to zero. A restriction on the magnitude of feasible controlling moment leads to the appearance of restricted intervals when spacecraft increases and decreases its angular velocity. These intervals lead to an increase in the angular momentum necessary on the stage of free rotation in order to comply with the given time T. The kinetic energy E_k increases (according to the constant proportion E_k/|L|²). The integral (5) increases also (as compared to the impulse, step-like control). Therefore, minimization of times of acceleration and deceleration is necessary. On the acceleration stage, the control problem is to transfer the spacecraft from the state ω(0)=0 to the state ω=${\omega }_{\text{cal}}$ in minimal time. On the deceleration stage, the control problem is to transfer the spacecraft from the state ω≠0 to the state ω(T)=0 in minimal time (in order that instant of beginning of braking is maximal not far from given time T).

In many cases of attitude control, the field of available moment M is described by the inequality

$M_1^2/J_1+M_2^2/J_2+M_3^2/J_3\le u_0^2$ (16)

where u₀>0 is some positive value specifying power of actuators of spacecraft attitude system.

In future, for finding the optimal rotation from position ${\Lambda }_{\text{in}}$ into position ${\Lambda }_{\text{f}}$ , let us assume that the moment M satisfy the condition (16). Laws of optimal control for fastest acceleration and braking are known when restriction on the controlling moment M has the form (16).²¹ For spin-up at minimal time, optimal moment M is calculated by the formula

$M_i=u_0{J}_i{\omega }_i/\sqrt{J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2}$ (17)

Optimal moment M and angular momentum L are parallel during acceleration at minimal time. Differentiation of left and right parts of equalities (17) gives the following differential equations (angular accelerations are taken from dynamic equations (1)):

${\dot{M}}_1={\omega }_3{M}_2-{\omega }_2{M}_3$ , ${\dot{M}}_2={\omega }_1{M}_3-{\omega }_3{M}_1$ , ${\dot{M}}_3={\omega }_2{M}_1-{\omega }_1{M}_2$ (18)

Rewrite last equations in vector form

$\dot{М}=-\omega \times M$

The obtained differential equation, for the controlling moment M, means its immobility relative to inertial coordinate system. As consequence, |M|=const during acceleration stage. For fastest braking, optimal moment M is

$M_i=-u_0{J}_i{\omega }_i/\sqrt{J_1{\omega }_1^2+J_2{\omega }_2^2+J_3{\omega }_3^2}$ (19)

After differentiation of equalities (19) we obtain differential equations (18) from which the property |M|=const appears for the entire braking stage. Thus, equality |M|=const is satisfied for optimal rotation during acceleration and braking phases. It is very important property of optimal motion and optimal control. Both at imparting the calculated angular momentum, and at damping of rotation, the moment M has constant magnitude (direction of vector M is not changed relative to inertial basis I); i.e. within acceleration and braking segments, optimal moment M is the fixed vector relative to inertial coordinate system.

For zero boundary conditions ω(0)=ω(Т )=0, slew maneuver includes two phases during which magnitude of the moment М is maximal possible: acceleration and braking, and phase of uncontrolled motion at which equations (13) are satisfied. A detailed analysis of the main reorientation stages: speedup, braking, and uncontrolled spacecraft rotation with constant kinetic energy and angular momentum (relative to inertial coordinate system), shows that all three stages have a common property, namely that spacecraft rotates along the “trajectory of free motion”. It is characteristic for the “trajectory of free motion” that the spacecraft’s angular momentum remains constant in inertial coordinate system. Taking into account that during the entire reorientation (on the entire time interval [0, T]) the torque M is parallel to the angular momentum vector L (i.e., either points in the same direction as L, or in the opposite direction, or equals zero), can conclude that M×L=0, and, therefore, there are no reasons for a rotation of the angular momentum L in inertial coordinate system.

For spacecraft reorientation with limited control, key property of optimal motion remains valid, the proportion E_k/|L|² between the kinetic energy E_k and angular momentum L is constant on the entire interval of time 0≤t≤T, independently of duration of acceleration and braking (independently of presence or absence of acceleration and braking stages). Angular momentum L and rotation energy E_k are continuous functions of time. Therefore, the proportion ρ=E_k/|L|² is continuous function. For acceleration (or braking), the equalities (17) (or (19)) and |M|=const are satisfied. Therefore, the proportion is constant within acceleration and braking. Between acceleration and braking, the equations (13) are satisfied; as result, ρ=const during free rotation. Hence, the proportion ρ=E_k/|L|²=const within time interval [0, T] because of a continuity of function ρ. As consequence, modulus of moment M is identical for acceleration and braking, and it is equal to same magnitude

$m_0=u_0/\sqrt{2\rho }=u_0/C$

since

$\left|M\right|=u_0\left|L\right|/\sqrt{2E_k}$

Angular momentum L does not change the direction relative to inertial coordinate system during acceleration, braking and at rotation between acceleration and braking (when spacecraft rotates by inertia), so, a direction of angular momentum in inertial coordinate system invariably on the entire interval of time [0, T]. Hence, in the presence of restriction (16), the equations (9) and (10) are satisfied at the entire interval of rotation from t=0 to t=Т. At acceleration and braking |М|=const=m₀, where m₀>0 is maximal admissible magnitude of the moment М in direction of angular momentum L. Since on entire interval of control J_i${\omega }_i$ //|L|=p_i , the value m₀ is identical during both phases of acceleration and braking, and it is equal u₀ /C, where C is the earlier introduced constant which is unambiguously specified by the vector p₀ and moments of inertia J₁, J₂ , J₃. The condition |M|≤m₀ is satisfied within the entire interval of control, where m₀=u₀/C. Optimal moment M is parallel to motionless line relative to inertial coordinate system. Direction of this motionless line is determined by direction of the vector p (since the directions of angular momentum L and the vector p coincide). Hence, M=m(t)p. The scalar function m(t) is specified as m(t)=(M₁L₁+M₂L₂+M₃L₃)/|L| or m(t)=M₁p₁+M₂p₂+M₃p₃. Control function m(t) is three-positional relay. The function m(t) can be written as: m(t)=m₀ if |L|<L_opt and t<T/2; m(t)=-m₀ if $t\ge T-\tau$ m(t)=0 if $\tau \le t<T-\tau$ . Here, L_opt is the modulus of angular momentum during free rotation; is duration of acceleration (braking) $L_{\text{opt}}=m_0\tau$ . Note the spacecraft’s angular momentum satisfies the inequality |L|£L_opt for any time t.

For optimal control, spacecraft acceleration continues until its angular momentum equals the target level

$L_{\text{tag}}=L_{\text{opt}}\circ \tilde{\Lambda }\circ {\Lambda }_{\text{in}}\circ p(0)\circ {\tilde{\Lambda }}_{\text{in}}\circ \Lambda$

The beginning of braking will be determined from the fact that as angular velocity ω reduces to zero, the angular momentum value |L (t)| changes linearly. During braking, the modulus of the controlling moment is constant, and the time moment from which braking will be started is specified by the following condition:

$4\text{arcsin}\frac{K\sqrt{{\delta }_2^2+{\delta }_3^2}}{\sqrt{{(J_2{\omega }_2)}^2+{(J_3{\omega }_3)}^2}}=\frac{K^2\sqrt{{\omega }_2^2+{\omega }_3^2}}{m_0\sqrt{{(J_2{\omega }_2)}^2+{(J_3{\omega }_3)}^2}}$

Where m₀ is the maximal controlling moment magnitude that can be provided by the actuators of spacecraft’s attitude control system; ${\delta }_j$ are the components of the discrepancy quaternion $\tilde{\Lambda }(t)\circ {\Lambda }_{\text{f}}$ ; К =|L(t)| is the current magnitude of the spacecraft’s angular momentum. The said condition for finding the start moment of braking phase allows the onboard control system to form the angular velocity reduction signal based on the information on current spacecraft orientation and measurements of its angular velocity. Use of this condition increases the precision of transferring the spacecraft into final position ${\Lambda }_{\text{f}}$ .

The case when the region of feasible controlling moments is given by inequality (16) was considered. The problem of optimal control of spacecraft orientation, when restriction has the form |M|≤m₀, is solved analogously. If control is limited by condition |M|≤m₀, then, in order to gain (suppress) the angular momentum L as fast as possible, it is necessary (and sufficient) that the moment M is parallel to the angular momentum L; speed of change of the angular momentum modulus (as a measure of motion intensity) does not depend on angular velocity. ω Optimal value of the moments M_i is

$M_i=\pm m_0{J}_i{\omega }_i/\left|L\right|$

(sign + corresponds to an acceleration, sign - corresponds to a braking).

Optimal moment M is collinear to the vector p which is unit vector of angular momentum L. Dependence of the controlling moment M on the vector p and all relations obtained for control function m(t) are true for optimal rotation under restriction |M|≤m₀. The system of equations (9), (10) is satisfied also.

Thus, we have arrived to the following conclusion: spacecraft reorientation with a minimal energy integral is performed along the “trajectory of free motion”, on which the direction of the spacecraft’s angular moment remains constant in inertial coordinate system on the entire time interval from t=0 to t=T. For cases when $\tau <<T$ the construction “acceleration of rotation, uncontrolled rotation, damping of rotation” is optimum for optimal control problem (2)-(5) if ω(0)=ω(T)=0 in slew maneuver. The assumed criterion of optimality provides spacecraft motion with minimal kinetic energy of rotation during reorientation maneuver. If at time moments t=0 and t=T the angular velocity ω changes abruptly, steplike, then the energy integral G and the reorientation time T would be inversely proportional to each other, and the level of kinetic energy E_k of the spacecraft rotation would relate to the reorientation time T as T²E_k=const=C²S².

Let us estimate the relative growth in functional G due to the nonzero time it takes to gain and suppress the angular momentum. As is know, value of the integral (15) does not depend on the character of variation of the angular momentum modulus if angular motion satisfies the system of equations (9), (10).²² For spacecraft motion along the “trajectory of free motion”, it holds that

$(T-(\Delta t_{\text{ac}}+\Delta t_{\text{br}})/2)L_{\text{opt}}=S$

because the modulus of angular momentum changes according to the linear law during optimal acceleration and braking, where L_opt is the magnitude of angular momentum between acceleration and braking (i.e. when condition |L|=const is satisfied); $\Delta t_{\text{ac}}$ and $\Delta t_{\text{br}}$ are the durations of gaining and suppressing the angular momentum, respectively. Therefore,

$L_{opt}=S/(T-(\Delta t_{ac}+\Delta t_{br})/2)$ , and$E_k=C^2{S}^2/(2{(T-(\Delta t_{\text{ac}}+\Delta t_{\text{br}})/2)}^2)$

The value of functional (5) equals

$G=G_{\text{opt}}T(T-2(\Delta t_{\text{ac}}+\Delta t_{\text{br}})/3){(T-(\Delta t_{\text{ac}}+\Delta t_{\text{br}})/2)}^{-2}$

Where G_opt is the value of the energy integral (5) for impulse control (when$\Delta t_{\text{ac}}$ ,$\Delta t_{\text{br}}\to 0$ ). The value G_opt is

G_opt=С²S²/Т

Absolute increase in integral (5) is $\Delta G=G-G_{\text{opt}}$ . Obviously, G is minimal when $\Delta t_{\text{ac}}+\Delta t_{\text{br}}$ =0; and minimal value of functional G is G_min=G_opt. If $\Delta t_{\text{ac}}+\Delta t_{\text{br}}$ >0, then a relative increase in the value of G will be$\Delta G/G_{\text{opt}}=T(T-2(\Delta t_{\text{ac}}+\Delta t_{\text{br}})/3){(T-(\Delta t_{\text{ac}}+\Delta t_{\text{br}})/2)}^{-2}-1$

The time-optimal reaching of the necessary angular momentum is done if the controlling moment and the spacecraft’s angular momentum have the same direction. The fastest reduction of the angular velocity is done if the controlling moment M is directed opposite to the spacecraft’s angular momentum. In our case, at the acceleration and deceleration stages, the magnitude of moment M is constant, time characteristics of the optimal motion program can be determined with sufficient precision. Since magnitude of the moment М is identical during acceleration and braking |M|=m₀=u₀/C (the constant C is introduced earlier), speedup time and braking time are identical, and nominal value L_opt=$m_0\tau$ , where $\tau$ is the time which is necessary to gain (suppressing) the angular momentum

$\tau =\frac{T}{2}\left(1-\sqrt{1-\frac{4S}{m_0{Т}^2}}\right)$

The relative “loss” will equal

$\Delta G/G_{\text{opt}}=T(T-4\tau /3){(T-\tau )}^2-1$

The less $\tau$ , the less the “loss”$\Delta G/G_{\text{opt}}$ will be. It becomes quite clear if to write

$\Delta G/G_{\text{opt}}=\frac{2\tau }{3(T-\tau )}-\frac{1}{3}{\left(\frac{\tau }{T-\tau }\right)}^2$

The time changes from zero to T/2. The function $\Delta G/G_{\text{opt}}$ increases everywhere in the range 0≤<$\tau$ T/2. The minimal value corresponds to the case τ→0, and the critical point (maximum) is the hypothetical case τ=T/2 as limit. The excess $\Delta G/G_{\text{opt}}$ will amount to a third of G_opt.

Let us give a numerical solution of optimal control problem for spacecraft reorientation with minimal value of the integral (5). As an example, let us consider spacecraft reorientation for 180 degree from initial position ${\Lambda }_{\text{in}}$ that corresponds to the attitude when body axes coincide with the axes of reference basis I into the target position ${\Lambda }_{\text{f}}$ . Let us assume that initial and final angular velocities are zero, ω(0)= ω(T)=0. Values of the elements of quaternion ${\Lambda }_{\text{f}}$ that characterizes the target spacecraft attitude are as follows:

${\lambda }_0$ =0 , ${\lambda }_1$ =0.707107 , ${\lambda }_2$ =0.59  ,${\lambda }_3$ =0.39

Let us find the optimal control program for the spacecraft rotation velocity ω(t) for transferring the spacecraft from the state $\Lambda (0)={\Lambda }_{\text{in}}$ , ω(0)=0 to the state $\Lambda (T)={\Lambda }_{\text{f}}$ , ω(T)=0. The constant u₀ which characterizes power of actuators is u₀=0.2 N kg^–1/2. The spacecraft’s mass-inertial characteristics are as follows:

J₁=77543.7 kg m², J₂=228466.1 kg m², J₃=175682.5 kg m²

Let us present a numerical solution of the spacecraft reorientation optimal control problem. Let the reorientation time be equal T=240 s. As a result of solving the kinematic reorientation problem of transitioning the spacecraft from position $\Lambda (0)={\Lambda }_{\text{in}}$ into position $\Lambda (T)={\Lambda }_{\text{f}}$ (the optimal reorientation problem in the impulse setting), the calculated value of vector p₀={0.485149; 0.126100; 0.865292} and integral S=401564.5 N ms² will be obtained According to these calculated values, the initial angular velocity equals ${\omega }_{\text{cal}}$ ={0.599785 ◦/s; 0.052913 ◦/s; 0.472173◦/s}. Iterations method guaranteeing successive approach to true value p₀¹¹ was used (in most cases, this method provides asymptotic approaching). The maximal value of the controlling moment is m₀=91.3 N m. The durations of speedup and braking is the same and equal to =20 s, while the angular momentum magnitude at the stage of rotation by inertia equals L_opt=1825.3 N m s.

Results of the mathematical modeling of the reorientation process under optimal control are given on Figure 1–4. Figure 1 shows the character of changing the angular velocities in the spacecraft-related system of coordinates ${\omega }_1$ (t), ${\omega }_2$ (t), ${\omega }_3$ (t) with respect to time. At the stage between spacecraft speedup and braking, the spacecraft rotates with constant energy equal to E_k=12.27 joules. The value of the energy integral, which characterizes the cost-efficiency of the rotation trajectory {$\Lambda$ (t), $\omega$ (t)} after spacecraft’s angular motion from position ${\Lambda }_{\text{in}}$ into position ${\Lambda }_{\text{f}}$ (the value of functional (5)) has been equal to G=5236 J s. Figure 2 shows the graphs of changes in the components of quaternion $\Lambda$ (t) that defines current spacecraft orientation in the process of the rotation maneuver: ${\lambda }_0$ (t), ${\lambda }_1$ (t), ${\lambda }_2$ (t), ${\lambda }_3$ (t). Figure 3 shows the dynamics of components p₁(t), p₂(t), p₃(t) of unit vector p in time. It is characteristic that that change of projection p₁  is very small in comparison with projections p₂ and p₃ (the angular velocity component ${\omega }_1$ also changes a lot less on the nominal rotation interval than angular velocity components ${\omega }_2$ and ${\omega }_3$ ). This confirms the fact that the OX axis is longitudinal axis. Unlike variables ${\omega }_i$ , variables p_i and ${\lambda }_j$ are smooth functions of time. Finally, Figure 4 shows the behavior of scalar function m(t). As it is well visible, change of function m(t) has relay character.

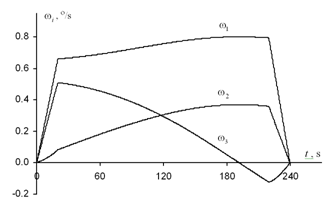
Figure 1 Changing the angular velocities during optimal reorientation maneuver.

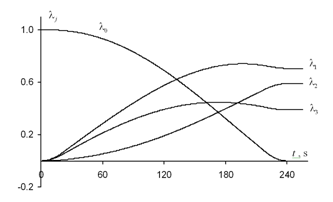
Figure 2 Changing the components of orientation quaternion Λ_(t)during optimal reorientation.

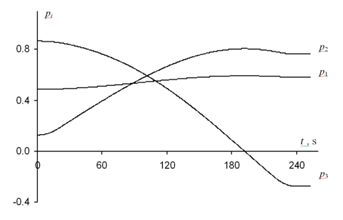
Figure 3 Changing the components of unit vector p in time under optimal control.

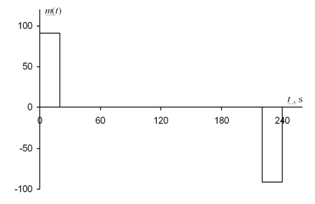
Figure 4 Changing the scalar function m(t) for optimal control.

Control algorithm of angular motion is very significant element of control system of spacecraft attitude, booster units and orbital stations. Designing optimal algorithm of controlling a spacecraft motion increases efficiency of onboard control system of a spacecraft and originates more economical performance of spacecraft during flight on orbit. In this paper, the optimal control problem for spacecraft’s spatial reorientation in given time is considered and solved. The optimization has been performed for case when rotation energy integral should be minimized. Finding the optimal mode of spacecraft reorientation with a minimal value of energy “expenditure” is quite topical. An analytic solution of the proposed problem is presented. Formal equations and computational expressions for constructing optimal reorientation program were obtained.

To solve the formulated problem, the optimality conditions in the form of the maximum principle are applied, and use of quaternions significantly simplifies computational procedures and reduces the computational costs of the control algorithm, which makes it suitable for onboard implementation. Mathematical expressions, which provide for obtaining final equations and relations describing the variation of control functions and behavior of a spacecraft during optimal slew maneuver, is based on universal variables which were introduced and investigated earlier.²⁰ First the main characteristic properties of optimal motion and the type of trajectory optimal with respect to the chosen criterion were determined. The kinematic reorientation problem has been solved completely. Necessary optimality conditions and determined the optimal control structure were found; formalized relations to determine the spacecraft’s optimal motion is obtained. After that, the spacecraft reorientation control problem with regard to the constraints on the controlling moment is studied. For a specific form of these constraints, the problem of optimal reorientation was solved.

It was demonstrated that optimal solution is two-impulse control. If controlling torque is limited, analytical formulas were written for duration acceleration and braking. It is shown that along the entire reorientation interval, direction of spacecraft’s angular momentum is constant in the inertial coordinate system, and the spacecraft rotates along the “trajectory of free motion”. A procedure for implementing the control mode is described. It is estimated how the duration of gaining and suppression of angular momentum influences energy costs. Expressions for computing temporal characteristics of the reorientation maneuver and the condition for finding the deceleration start moment based on factual kinematic motion parameters judging by terminal control principles are presented, which leads to high orientation precision. Example and results of mathematical modeling for spacecraft motion under optimal control are given.

Thus, key results are the following: the carried out research has reached an overall objective since optimal control program of spacecraft reorientation with minimal rotation energy within given time interval was found; it was demonstrated that two-impulse control when spacecraft rotates by inertia between acceleration and braking is optimum; for optimal solution, estimations of the relative growth in the functional of quality due to the limited controlling moment were done. Other characteristic properties of the obtained optimal motion are determined also. All conclusions are absolutely true since well-known mathematical methods were used, and all mathematical formulas are based on the checked theories. For a dynamic symmetric spacecraft, a complete solution of the reorientation problem in closed form is presented; optimal values of control law parameters can be found by the device.²⁹ The obtained results demonstrate that the designed control method of spacecraft's three-dimensional reorientation is feasible in practice.

No financial exists.

No conflicts of interest exist.

1. Branets VN, Shmyglevskii IP. Use of quaternions in the problems of orientation of solid bodies. 1973.
2. Alekseev KB, Malyavin AA, Shadyan AV. Extensive control of spacecraft orientation based on fuzzy logic. Flight 1. 2009;47–53.
3. Raushenbakh BV, Tokar’ EN. Spacecraft orientation control.1974;600.
4. Ermoshina OV, Krishchenko AP. Synthesis of programmed controls of spacecraft orientation by the method of inverse problem of dynamics. Journal of Computer and Systems Sciences International. 2000;39(2):313–320.
5. Velishchanskii MA, Krishchenko AP, Tkachev SB. Synthesis of spacecraft reorientation algorithms using the concept of the inverse dynamic problem. Journal of Computer and System Sciences International. 2003;42(5):811–818.
6. Li F, Bainum PM. Numerical approach for solving rigid spacecraft minimum time attitude maneuvers. Journal of Guidance, Control, and Dynamics. 1990;13(1):38–45.
7. Scrivener S, Thompson R. Survey of time-optimal attitude maneuvers. Journal of Guidance, Control, and Dynamics. 1994; 17(2):225–233.
8. Liu S, Singh T. Fuel/time optimal control of spacecraft maneuvers. Journal of Guidance. 1996;20(2):394–397.
9. Byers R, Vadali S. Quasi-closed-form solution to the time-optimal rigid spacecraft reorientation problem. Journal of Guidance, Control, and Dynamics. 1993;16(3):453–461.
10. Junkins JL, Turner JD. Optimal spacecraft rotational maneuvers. Elsevier. 1986;534.
11. Levskii MV. Pontryagin’s maximum principle in optimal control problems of orientation of a spacecraft. Journal of Computer and System Sciences International. 2008;47(6):974–986.
12. Shen H, Tsiotras P. Time-optimal control of axi-symmetric rigid spacecraft with two controls. Journal of Guidance, Control, and Dynamics. 1999;22(5):682–694.
13. Molodenkov AV, Sapunkov YaG. A solution of the optimal turn problem of an axially symmetric spacecraft with bounded and pulse control under arbitrary boundary conditions. Journal of Computer and System Sciences International. 2007;46(2):310–323.
14. Molodenkov AV, Sapunkov YaG. Special control regime in the problem of optimal turn of an axially symmetric spacecraft. Journal of Computer and System Sciences International. 2007;49(6):891–899.
15. Kovtun VS, Mitrikas VV, Platonov VN, et al. Mathematical support for conducting experiment with attitude control of space astrophysical module Gamma. Technical Cybernetics. 1990;3:144–157.
16. Platonov VN, Kovtun VS. Method for spacecraft control using reactive actuators during execution of a programmed turn. 1997.
17. Levskii MV. Features of attitude control of a spacecraft, equipped with inertial actuators. Mechatronics, Automation, Control. 2015;16(3):188–195.
18. Levskii MV. Special aspects in attitude control of a spacecraft, equipped with inertial actuators. Journal of Computer Science Applications and Information Technology. 2017;2(4):1–9.
19. Levskii MV. Method of Controlling a Spacecraft Turn. 1997;271.
20. Levskii MV. The use of universal variables in problems of optimal control concerning spacecrafts orientation. Mechatronics, Automation, Control. 2014;1:53–59.
21. Levskii MV. On optimal spacecraft damping. Journal of Computer and System Sciences International. 2011;50(1):144–157.
22. Levskii MV. Optimal spacecraft terminal attitude control synthesis by the quaternion method. Mechanics of Solids. 2009;44(2):169–183.
23. Levskii MV. Method of spacecraft turns control and the system for its realization. Inventions Applications and Patents.1998.
24. Levskii MV. Control system of spatial turn of a spacecraft. Inventions Statements and Patents. 1994;49–50.
25. Krasovskii AA. Handbook on the Automatic Control Theory. 1987;712.
26. Pontryagin LS, Boltyanskii VG, Gamkrelidze RV, et al. The mathematical theory of optimal processes. Gordon and Breach: USA; 1987. p. 360.
27. Young LG. Lectures on the calculus of variations and optimal control theory. WB Saunders Company: USA;1969.
28. Markeev AP. Theoretical mechanics. 414 p.
29. Levskii MV. Device for regular rigid body precession parameters formation. Inventions Applications and Patents. 2000.
30. Lastman G. A shooting method for solving two-point boundary-value problems arising from non-singular bang-bang optimal control problems. International Journal of Control. 1978;27(4):513–524.
31. Bertolazzi E, Biral F, Da Lio M. Symbolic-numeric efficient solution of optimal control problems for multibody systems. Journal of Computational and Applied Mathematics. 2006;185(2):404–421.
32. Kumar S, Kanwar V, Singh S. Modified efficient families of two and three-step predictor-corrector iterative methods for solving nonlinear equations. Journal of Applied Mathematics. 2010;1(3):153–158.