Planet Earth faces the problem of global warming. Recent research on the dynamics of the CO₂ concentration in the atmosphere has shown how reductions of global industrial emissions of CO₂ can solve a large part of the global warming problem. However, there are more control options available. Our world is covered by large areas of primary (natural) forests that are almost not managed at all. They do not contribute very much to the net absorption of CO₂. Parts of these natural forests may be transformed to continuous cover forests, which mean that the absorption of CO₂ increases so that the CO₂ level in the atmosphere can be further reduced. This transformation can be made without severely damaging the environmental conditions. The analysis in this paper shows how to define an optimization problem with two objectives with different weights in the objective function. These objectives are the economic present value of profits and the utility of the climate. The analysis shows how the optimal transformation of natural forests to managed continuous cover forests is affected by the relative weights of the utility of the climate and of the present value of the profits. If the relative weight of the utility of the climate increases, the optimal area of natural forests that should be transformed to managed continuous cover forests increases. If 600 M hectares are transformed during 60 years, from 2020 until 2080, then the concentration of CO₂ in the atmosphere can be reduced by 8 ppm until the year 2100.

Keywords: optimization, climate, forest management, continuous cover forestry, differential equations

Global warming is a well-known problem of our world. Lohmander P, et al. 2020¹ gives a review of the literature on fundamental physical facts. He also develops a theory of the CO₂ dynamics and shows how the future development of the CO₂ concentration in the atmosphere can be predicted via a forced differential equation. The theory of differential equations is well described by Braun M. 1983.² The forcing function is based on the global emissions of CO₂ from power plants, industrial emissions, traffic and other sources. With alternative levels of reduction of the global CO₂ emissions, it is possible to change the time path of the CO₂ concentration in the atmosphere in different ways. The article shows a number of alternative possibilities.

In this paper, the analysis will be further developed. We will not only consider the effects of global emissions on the CO₂ development. In the forcing function, we will also consider the possibility to increase the absorption of CO₂ via expansion of the area of managed forests.

Our planet Earth is covered by very large areas of forests. Some of these forests are intensively managed in different ways, via clear cut systems or via continuous cover forestry systems. Usually, the more intensively managed forests are located close to strongly populated and industrialized areas.

FAO, 2020³ reports that the total forest area is 4.06 billion hectares (ha), which represents 31% of the total land area. The countries that have the largest forest areas are Russian Federation (815 M ha), Brazil (497 M ha), Canada (347 M ha), USA (310 M ha) and China (220 M ha). 93% of the world forest area (3.75 billion ha) contains naturally regenerating forests and 7% contains forest plantations.

According to FAO, 2020³ the world presently has at least 1.11 billion ha of primary forest. In these primary forests, of particular interest and relevance to the analysis developed in the later part of this paper, there are practically no human activities such as forest harvesting. The forests are almost undisturbed by human industrial projects and have native forest species and original ecological processes. In the three countries Brazil, Russian Federation and Canada, we find 61% of these primary forests, which represents approximately 677 M ha.

Hence, in more remote areas, in particular in Russian Federation, Canada and Brazil, large forest areas are in a more or less natural state. There, almost no harvesting takes place. Furthermore, old and tall trees are often damaged by insects, wild fires and storms. Then they fall and burn and the CO₂ contents of the trees are released to the atmosphere. New young trees are produced by the natural seeds and the forest sequentially reproduces itself. Then, the CO₂ from the atmosphere is once again stored in large trees.

In the long run, the average amount of CO₂ stored in these primary forests is almost constant. The average net absorption of CO₂ from the atmosphere is, in these forests, very close to zero. It is sometimes true that the amount of CO₂ stored in the roots may grow over time. That amount of CO₂ absorption is however usually much lower than the amount of absorption in managed forests.

In this paper, we will define an optimization problem in which we determine the optimal path of expansion of CCF, Continuous Cover Forestry, in the world. One reason why CCF is the suggested form of forestry is that natural forests can be rapidly transformed to CCF forests without complete destruction of the environmental conditions of relevance to animals, plants and humans. Furthermore, transformation of undisturbed natural forests to CCF forests imply that we start with removal of several large trees, that instantly can replace some of the fossil fuels such as coal in combined heat and power stations. One strong production economic reason is that the total present value of transforming a natural forest to a CCF forest many times can be shown to be higher than the present value of a clear felling of the existing trees followed by plantation investments. Of course, the transformation decisions concerning stock levels, species proportions, harvesting intervals etc. should be optimized. Several studies on optimization of forest management that are relevant to more detailed decisions of this type are found in Lohmander P, 2000, 2007, 2019, 2019.^4,5,6,7

In order to make the analysis completely transparent, the expansion will be defined via two decision variables, namely the area expansion per year and the total number of years when the area expansion should take place. Of course, forest conditions of many kinds differ between countries and regions. However, we may expand CCF simultaneously in many regions. This way, the average conditions of relevance to the global effects on total CO₂ absorption, the revenue and cost function parameters, can be treated as constants. In future more detailed analyses of this type; we may explicitly consider regional differences and options. Many theories and methods are available for operations research expansions of this topic area. Several relevant methodological options for such developments are found in Nemati, et al., 2017,⁸ Rasay, et al., 2018,⁹ Yadegari, et al., 2015¹⁰ and Yosefnajad, et al., 2019.¹¹ Rideout, et al., 2008¹² and Lohmander P, 2018¹³ contain more ideas concerning how total optimization of the forestry sector should be obtained. At this stage, an increased level of detail would however decrease the transparency of the calculations.

In the analyses of this paper, some conditions are well studied and quantified. The forced differential equation of the CO₂ concentration dynamics has already been estimated. Hence, the effects of alternative changes of global emissions and different levels of absorption from changing forest management can be predicted with high accuracy over long horizons. Other factors, such as revenues and costs, are not easily estimated and predicted over a long horizon. The analysis of this paper concerns a land use transformation project with global dimensions and a scale that has never been tried before. Furthermore, over time, technological inventions and changes in the factor and product markets can be expected to modify relevant revenue and cost functions. The analysis performed however requires revenue and cost functions to give an understanding of the central considerations that should be made. For these reasons, the economically dependent revenue and cost functions that are used in the present version of the optimization model should be understood as possible examples of such functions. The revenue and cost functions may be updated as soon as such functions have been estimated. Such estimations are large and complicated projects, far beyond the scope of this paper.

The optimization problem in brief

Considering the global warming situation; how should we optimally transform a part of the presently existing primary (natural) forests to managed continuous cover forests? A connected problem has been analyzed by Lohmander P, 2020.¹⁴

The decisions to be optimized are the speed of CCF area expansion (area expansion per year) and the number of years when CCF should be expanded.

Two kinds of objectives are considered, namely: The economic present value of profits and the utility of the climate. We want to investigate how the optimal decisions change if we modify the relative weights of the different objectives in the objective function of the optimization.

The development of the climate is described via the dynamics of the CO₂ concentration in the atmosphere, according to the forced differential equation estimated in Lohmander P, 2020.¹ The differential equation is marginally adjusted via the decision variables that are optimized in this analysis, since they change the area of actively managed forests. The absorption of CO₂ is an increasing function of the area of actively managed forests.

In order to avoid confusion with the notation and since a numerical optimization model is used in the analysis, all variables, parameters and equations are written in the same format as in the software. 

The optimization problem in detail

The optimization problem contains the objective function OBJF:

$OBJF=kW*W+kR*PVR-kC*PVC$

Time is denoted by t, in years. t = 0 in year 2020. The analysis is concerned with the time interval year 2020 until year 2100, which means that t goes from 0 to 80. The time horizon is denoted T. T = 80. W(t) is the utility of the climate as a function of time. W = W(T), is the utility of the predicted climate at the time horizon, T.  The utility is assumed to be a strictly concave function of the CO₂ concentration in the atmosphere. This utility function has a unique maximum at the CO₂ level 280 ppm, which is assumed to be the “preindustrial level”.

Net revenues are defined as revenues minus variable costs. PVR and PVC denote the present values of the net revenues and investment costs, respectively, of the CCF forestry expansion during the time period, year 2020 until the time horizon, year 2100. PVR and PVC should include all relevant revenues and costs associated with the area expansion, including initial road and railroad construction, harvesting, terrain transport and economic valuations of changes of environmental conditions etc.

We will investigate how the complete system and the optimal decisions change if we change the weight of the utility of climate in the objective function. In the analyzed cases, the utility of the climate, W, is given different levels of weight in the objective function in relation to the weight of the net present value of the profits. kW, kR and kC denote the weights of the different objectives in the objective function. In all analyzed cases,   $kR=kC=1.$

The decision variables, that are optimized, are y1opt and ytopt.

ytopt denotes the number of years during which the area expansion should take place. The expansion starts at time zero, year 2020. The expansion ends at time ytopt, which is year 2020 + ytopt. y1opt denotes the area expansion per year, during the time interval year 2020 until year 2020 + ytopt. ytotopt, is a function of y1opt and ytopt. This is the total area expansion during the period 2020 until year 2020 + ytopt.

Since the optimization problem is defined with a linear area expansion policy, there are only two decision variables, y1opt and ytopt. This makes it possible to rapidly investigate the values of the objective function in the complete decision space in very high resolution. This way, the globally optimal decision combination can be determined without the risk of being trapped in one of many local optima. We do not have to investigate the second order properties of the objective function, problems with economies of scale etc. Multiple local optima often cause problems if we use gradient methods, the Newton Raphson method etc.

Of course, several parameters in the problem definition are dependent on many local conditions, all of which cannot be discussed in detail. The presented results are based on some assumptions that can be modified by the reader. Since the included software is programmed in the language QB64, which can be downloaded for free via the Internet, the interested reader can adjust the parameter values and execute the adjusted software. Then, locally relevant results can be derived. 

The optimization model

Definitions of files, parameters and tables: First, an output file is defined. Then, a number of tables (Appendix) and parameters are specified.

x(t) is the amount of CO₂ in the atmosphere in the unit Gt, Giga tonnes, and xppm(t) is the concentration of CO₂ in the atmosphere in the unit ppm. u(t) is the CCF area expansion year 2020 + t and y(t) is the total area of expansion from year 2020 until year 2020 + t. disc (t) denotes the discounting factor of year 2020 + t.    

The initial CO₂ concentration is defined according to the results from Lohmander P, 2020.¹

$\begin{array}{l}X\left(0\right)=3230.747\hfill \\ Xppm\left(0\right)=413.96911\hfill \end{array}$

These atmospheric parameters are calculated by Lohmander P, 2020.¹:

$\begin{array}{l}a0=40.951\hfill \\ ax=-0.0187191\hfill \end{array}$

The real rate of interest in the capital market is defined to be 3%, in continuous time.

$R=0.03$

The ”climate utility function” is defined as a quadratic function of xppm(t) with these parameters:

$\begin{array}{l}wx=0.7142857\hfill \\ wxx=-0.001275510\hfill \end{array}$

The net revenue function is defined as a quadratic function with these parameters:

$\begin{array}{l}Ry=0.2\hfill \\ Ryy=-0.0002\hfill \end{array}$

The investment cost function is defined as a quadratic function with these parameters:

$\begin{array}{l}Cu=2\hfill \\ Cuu=0.2\hfill \end{array}$

The objective functions weights are given these default values:

$kW=1,kR=1,kC=1$

A loop with different values of the weight of W in the objective function is started: Within the loop with different values of the weight of W, there is a two dimensional search loop in which the optimal decision combination is determined.

Search for the optimal combination of the decision variables: The initial objective function value is set to a value that is far below the optimal value.

Then, a double loop is defined where all possible combinations of the two decision variables are tested. One differential function of the CO₂ concentration is determined from the values of the emission reduction scenario and the values of the two decision variables for the period from year 2020 until the year when the area expansion stops. The original version of this differential equation is derived and explained in detail in Lohmander P, 2020.¹ In the following code section, in the third row, we see that y1 has the coefficient -0.003. This is an adjustment of the original function from Lohmander P, 2020.¹ The reason for this adjustment is the assumption that one million hectares of CCF forest on average implies a net absorbtion of  0.003 Gt of CO₂ each year. This corresponds to 3 tonnes of CO₂ per hectare, which can be considered as a typical value in forestry in the regions where transformations are most likely to occur. The reader may modify this coefficient and determine alternative solutions.

Period 1 (year 2020 until year 2020 + yt)         

$\begin{array}{l}x0=3230.747\hfill \\ m0=38.8818\hfill \\ m1=-0.48602-0.003*y1\hfill \\ k1=-m1/ax\hfill \\ k0=-\left(a0+m0+m1/ax\right)/ax\hfill \\ \hfill \\ FORt=0TOyt\hfill \\ x\left(t\right)=\left(x0-k0\right)*EXP\left(ax*t\right)+k0+k1*t\hfill \\ y\left(t\right)=y1*t\hfill \\ u\left(t\right)=y1\hfill \\ NEXTt\hfill \end{array}$

Another differential function of the CO2 concentration is determined from the values of the emission reduction scenario and the values of the two decision variables for the year when the area expansion stops until year 2100.

Period 2 (year 2020+yt+1 until year 2100)       

$\begin{array}{l}x02=x\left(yt\right)\hfill \\ m02=m0+m1*yt\hfill \\ m12=-0.48602\hfill \\ k12=-m12/ax\hfill \\ k02=-\left(a0+m02+m12/ax\right)/ax\hfill \\ \hfill \\ FORt=\left(yt+1\right)TO80\hfill \\ t2=t-yt\hfill \\ x\left(t\right)=\left(x02-k02\right)*EXP\left(ax*t2\right)+k02+k12*t2\hfill \\ y\left(t\right)=y1*yt\hfill \\ u\left(t\right)=0\hfill \\ NEXTt\hfill \end{array}$

The time path of the CO₂ concentration during the time interval 2020 until 2100 is determined. All net revenues, investment costs and climate utility values are calculated for every year from 2020 until 2100.

The total objective function value is calculated for the particluar combination of decision variables.

For every new combination, in case the new objective function value is higher than the earlier found highest objective function value, the new solution replaces the earlier best solution. When all possible decision combinations have been investigated, the optimal solution is defined as the solution that gave the highest objective function value among all investigated decision combinations.

Optimal results are printed: Finally, the central results are printed as a text file that can be used for construction of graphical figures. These are shown as Figure 1 to 7.

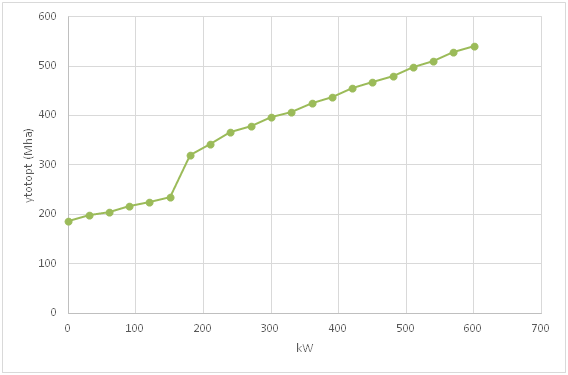
Figure 1 ytotopt, the optimal total area of CCF expansion, as a function of kW, the weight of W in the objective function. ytotopt is a function of ytopt and y1opt. These are found in Figures 2 & 3.

In Figure 1, we see that the total area of CCF expansion is an increasing function of kW, the weight of the utility of climate in the objective function. This is a logical result. If the importance of reaching a cooler climate, with a lower level of CO₂ in the atmosphere increases, it is more important to increase the CO₂ absorption of the forests of the world. In other words, the total area of CCF expansion should increase.

In Figures 2 & 3, we obtain more details concerning the optimal CCF area expansion. The optimal expansion per year, found in Figure 3, is an increasing function of the weight of W, which should be expected. One exception is however found in Figure 3 where kW goes from 150 to 180. In that interval, however, ytopt increases very much. Hence, the total area expansion, ytotopt, is an increasing function of kW also when kW goes from 150 to 180.

Figure 2 ytopt, the optimal number of years to continue the CCF expansion, as a function of kW, the weight of W in the objective function.

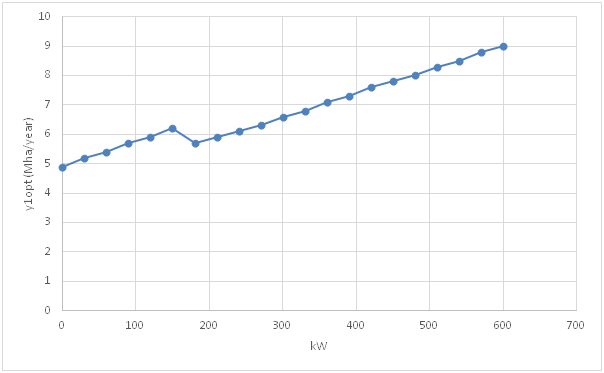
Figure 3 y1opt, the optimal area expansion of CCF per year, until year ytopt, as a function of kW, the weight of W in the objective function.

In Figure 4, we see how the optimal concentration of CO₂ in year 2100 decreases if the utility of the climate is given more weight in the objective function.

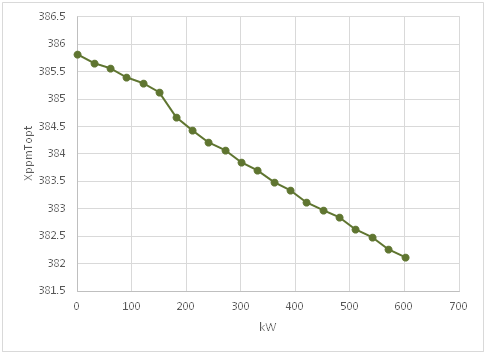
Figure 4 XppmTopt, the optimal ppm value of CO2 at time T, (the year 2100), as a function of kW, the weight of W in the objective function.

The present value of net revenues is an increasing and concave function of the weight of W in the objective function. This is shown in Figure 5 and is an expected result. The reason is that the volume of harvested wood is an increasing function of the area of CCF and that the area of CCF is an increasing function of the importance of reducing the global warming. The function is concave since the marginal value of wood is a decreasing function of the total amount of wood in the market.

Figure 5 PVRopt, The optimal present value of net revenues, PVCopt, the optimal present value of investment costs and PV, the optimal present value of the profits, as functions of kW, the weight of W in the objective function.

The present value of the investment costs of the area expansion is also an increasing function of the weight of W in the objective function. This is also found in Figure 5 and has the following reason: The investment costs of the area expansion increase since more roads and railroads should be constructed. Furthermore, the area of CCF is an increasing function of the importance of reducing the global warming.

The present value of profits, net revenues minus investment costs, has a maximum where the weight of W in the objective function is zero. This is logical since the objective function then only contains the present value of the profits, which is maximized. The present value is a decreasing function of the weight of W in the objective function. For very high values of the weight of W in the objective function, the present value of the profits becomes negative.

The frontier of optimal combinations of the present value of the profits and the concentration of CO₂ in the atmosphere at time T (year 2100) is illustrated in Figure 6. The curve has been constructed from many different points, representing optimal solutions. These solutions were determined via optimization of the objective function with different weights of the utility of climate, W, when the weight of the present value of profits was held constant. If we want to obtain a higher level of utility from the climate, via a lower level of CO₂ concentration, it is necessary to increase the level of CCF area expansion above the economically optimal level, which means that the present value of net revenues minus investment costs decreases.

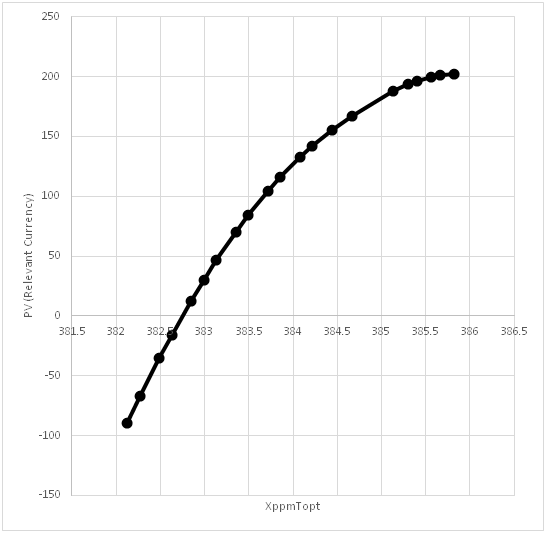
Figure 6 The frontier of optimal combinations of PV, the present value of the profits, and XppmTopt, the concentration of CO2 in the atmosphere at time T (year 2100). In different points along the curve, the relative weights of the different objectives in the objective function are different.

In Figure 7, we find the time path of the CO₂ concentration in the atmosphere as a function of the number of years with CCF expansion. Three cases are illustrated. The graphs are based on one of the global emission reduction cases defined in Lohmander P, 2020.¹ We may use the graph to investigate how much we have to expand CCF in order to reduce the concentration of CO₂ with a particular amount. For instance, a 600 M ha area expansion may reduce the concentration of CO₂ in year 2100 by 8 ppm (from 389 ppm to 381 ppm). Furthermore, we should remember that the CO₂ concentration reduction is strongly affected by the selected time path of the emission reductions. Alternative emission reduction cases are found in Lohmander P, 2020.¹

Figure 7 The time path of the CO2 concentration in the atmosphere, Xppm, over time as a function of yt, the number of years with CCF expansion. Three cases are illustrated. In all cases, the CCF expansion per year is 10 Mha, until the expansion stops. In xppm_0, the CCF expansion instantly stops (it never starts), in xppm_30, the CCF expansion stops after 30 years (in year 2050) and in xppm_60, the CCF expansion stops after 60 years (in year 2080). All cases reported in this graph are based on a particular general global emission reduction case defined in Lohmander P, 2020.1 The emission reduction per year, in this case, from year 2020, is constant until year 2100. In year 2100, the emissions are zero.

Our world is covered by large areas of primary (natural) forests. They do not contribute very much to the net absorption of CO₂. Parts of these natural forests may be transformed to continuous cover forests, which mean that the absorption of CO₂ increases so that the CO₂ level in the atmosphere can be further reduced. This transformation can be made without severely damaging the environmental conditions. The analysis in this paper shows how to define an optimization problem with two objectives with different weights in the objective function. These objectives are the present value of profits and the utility of the climate. The analysis shows how the optimal transformation of natural forests to managed continuous cover forests is affected by the relative weights of the utility of the climate and of the present value of the profits. If the relative weight of the utility of the climate increases, the optimal area of natural forests that should be transformed to managed continuous cover forests increases. If 600 M hectares are transformed during 60 years, from 2020 until 2080, then the concentration of CO₂ in the atmosphere can be reduced by 8 ppm until the year 2100.

Today, the leaders of our world face a unique challenge. One way or another, the global warming problem must be solved in order to make it possible for future generations to survive on planet Earth. Planet Venus is a warning. There, the green house gases make the temperature reach hundreds of degrees Celsius.

The analysis in this paper has shown that transformation of large natural forests to environmentally acceptable managed continuous cover forests can be one of the tools that may be used to reduce global warming. Still, as the results show, even if the enormous area of 600 M ha is transformed this way, the CO₂ concentration in the atmosphere does not decrease more than about 8 ppm until year 2100. It is important to be aware that this result is dependent on the assumption that the average net absorption of CO₂ in continuous cover forests is 3 ton per hectare. That figure can be considered as typical in several regions that have natural forests that may be transformed to continuous cover forests, for instance in Russian Federation and Canada. 

Whatever we do with the forests, the most rational tools of emission reduction should be used. The global fossil emissions of CO₂, from industry, power plants and traffic, should be strongly reduced, as shown by Lohmander P, 2020.¹ in order to reach stable and acceptable CO₂ concentration levels in the atmosphere.

The transformation of natural forests to managed continuous cover forests with acceptable environmental conditions, is however an important complement to other approaches.

In order to become more specific in the planning of transformation processes of the type suggested in this paper, studies of revenue and cost functions of relevance to the optimization problem are encouraged. Furthermore, utility functions associated with different climatic situations, should be estimated in different regions. With more empirical data and functions of these types, the transformation processes can soon be planned and executed.

Of course, some regions may benefit more than others from a cooler climate and some regions may have more options to undertake concrete actions that can influence the global climate. Hence, there are several unavoidable international negotiation processes that should be started to solve the global warming problem in the best way.  This paper does not handle or try to solve these negotiations problems. It is however necessary that these processes are initiated as soon as possible. Hopefully, the presented analysis can be one of the components in this process.

None.

None.

The author declares that there was no conflict of interest.

1. Lohmander P. Dynamics and control of the CO2 level via a differential equation and alternative global emissions strategies. International Robotics & Automation Journal. 2020;6(1):7–15.
2. Braun M. Differential equations and their applications. USA: Springer; 1983.
3. FAO. Global Forest Resources Assessment 2020, Key findings. Italy: FAO; 2020.
4. Lohmander P. Optimal sequential forestry decisions under risk. Ann. Oper. Res. 2000;95:217–228.
5. Lohmander P. Adaptive Optimization of Forest Management in a Stochastic World. In: editors, Weintraub A, Romero C, Bjorndal T, et al. Handbook of Operations Research in Natural Resources. Springer: USA; 2007. pp. 525–544.
6. Lohmander P. Control function optimization for stochastic continuous cover forest management. International Robotics and Automation Journal. 2019:5(2):85–89.
7. Lohmander P. Market Adaptive Control Function Optimization in Continuous Cover Forest Management. Iranian Journal of Management Studies. 2019;12(3):335–361.
8. Nemati Y, Madhoushi M, Safaei Ghadikolaei A. Towards Supply Chain Planning Integration: Uncertainty Analysis Using Fuzzy Mathematical Programming Approach in a Plastic Forming Company. Iranian Journal of Management Studies. 2017;10(2):335–364.
9. Rasay H, Fallahnezhad M, Zaremehrjerdi Y. Integration of the Decisions Associated with Maintenance Management and Process Control for a Series Production System. Iranian Journal of Management Studies. 2018;11(2):379–405.
10. Yadegari E, Najmi H, Ghomi-Avili M, et al. A Flexible Integrated Forward/ Reverse Logistics Model with Random Path-based Memetic Algorithm. Iranian Journal of Management Studies. 2015;8(2):287–313.
11. Yousefnejad H, Rabbani M, Manavizadeh N. A Simulation-Optimization Model For Capacity Coordination In Make To Stock/Make To Order Production Environments. Iranian Journal of Management Studies. 2019;12(2):235–253.
12. Rideout DB, Wei Y, Kirsch AG, et al. Toward a unified economic theory of fire program analysis with strategies for empirical modelling. In:  editors, TP Holmes, Prestemon JP, Karen A. The Economics of Forest Disturbances: Wildfires, Storms and Invasive Species. Springer: USA; 2008. pp. 361–380.
13. Lohmander P. Applications and Mathematical Modeling in Operations Research. In: editors, Cao BY, Fuzzy Information and Engineering and Decision. Springer: USA; 2017.
14. Lohmander P. Fundamental principles of optimal utilization of forests with consideration of global warming and other related objectives. Central Asian Journal of Environmental Science and Technology Innovation. 2020;1(3):171–180.