eISSN: 2574-8092


Research Article Volume 5 Issue 5
Optimal Solutions in cooperation with Linnaeus University, Sweden
Correspondence: Peter Lohmander, Optimal Solutions in cooperation with Linnaeus University, Umea,Sweden
Received: October 17, 2019 | Published: October 31, 2019
Citation: Lohmander P. Optimal decisions and expected values in two player zero sum games with diagonal game matrixes-explicit functions, general proofs and effects of parameter estimation errors. Int Rob Auto J . 2019;5(5):186-198. DOI: 10.15406/iratj.2019.05.00193
In this paper, the two player zero sum games with diagonal game matrixes, TPZSGD, are analyzed. Many important applications of this particular class of games are found in military decision problems, in customs and immigration strategies and police work. Explicit functions are derived that give the optimal frequences of different decisions and the expected results of relevance to the different decision makers. Arbitrary numbers of decision alternatives are covered. It is proved that the derived optimal decision frequency formulas correspond to the unique optimization results of the two players. It is proved that the optimal solutions, for both players, always lead to a unique completely mixed strategy Nash equilibrium. For each player, the optimal frequency of a particular decision is strictly greater than 0 and strictly less than 1. With comparative statics analyses, the directions of the changes of optimal decision frequences and expected game values as functions of changes in different parameter values, are determined. The signs of the optimal changes of the decision frequences, of the different players, are also determined as functions of risk in different parameter values. Furthermore, the directions of changes of the expected optimal value of the game, are determined as functions of risk in the different parameter values. Finally, some of the derived formulas are used to confirm earlier game theory results presented in the literature. It is demonstrated that the new functions can be applied to solve common military problems.
Keyword: optimal decisions, completely mixed strategy Nash equilibrium, zero sum game theory, stochastic games
What is the optimal strategy of a decision maker, BLUE, such as an individual or organization, when at least one more decision maker, RED, can influence the outcomes? This is a typical question in game theory.
Game theory is a field of research that contains large numbers of studies with different assumptions concerning the number of players, the kinds of decisions that can be taken by the different participants and the degree of information available to the different decision makers at different points in time.
Luce and Raffa1 give a general description of most of the game theory literature. Some of the highly important and original publications in the field are Nash,2 von Neumann,3 and Dresher4. Chiang5 covers two person zero sum games and most other methods and theories of general mathematical economics. Isaacs6 develops dynamic games with and without stochastic events in continuous and discrete time. In Braun7 we find a section where differential equations are used to model and describe the development of games of conflict with several examples of real applications.
Lohmander8 contains a new approach to dynamic games of conflict with two players. It includes a stochastic dynamic programming, SDP, model with a linear programming, LP, or quadratic programming, QP, model as a sub routine. The LP or QP can be used to solve static game problems, such as two person zero sum games, TPZSGs, for each state and stage in the SDP model. The outcomes of the repeated games move the positions in state space (change the states to new states) with different transitions probabilities, in the following periods, within the SDP model. The SDP model solves the complete dynamic and stochastic game over a time horizon with several periods.
During the history of game theory, the TPZSGs have always gained considerable theoretical and practical interest. A detailed treatment is given by Luce and Raffa.1 Several kinds of TPZSGs with large numbers of military applications are well described by Washburn.9 This can serve as a good introduction to the analysis in this paper. A Nash equilibrium is the normal outcome of LP solutions to TPZSGs. It is however important to be aware that the Nash equilibrium can not always be expected to be the result in real world games. If the strategies of the players are gradually adjusted based on the observations of the decision frequences of the other players, mixed strategy probability orbits (constrained cycles) may develop. Convergence to the Nash equilibrium can not always be expected. Lohmander10 has developed a dynamic model and described these possibilities. Herings et al11 focuses on stationary equilibria in stochastic games. They are interested in model structure, selection and computation. Babu et al12 give a good historical introduction to the literature on stochastic games. They also develop some new results in the area of equilibrium strategies of dynamic games based on mixed strategy assumptions within static games.
In this paper, a particular class of TPZSGs will be analyzed, namely two player zero sum games with diagonal game matrixes were all diagonal elements are strictly positive. Let us denote them TPZSGDs. This may seem to be a highly particular, constrained and irrelevant class of games. However, this is not true. A large number of obvious and economically very important real world applications of this class of games exist, in particular in military applications, in customs problems and in police work. Lohmander13 defines, describes and solves four different types of military TPZSGD decision problems with this methodology. These problems include:
Game theory literature usually focuses on very general classes of games, without giving special attention to the TPZSG, and the even more specific TPZSGD, classes.
In this paper, explicit functions of the optimal decision frequences and the expected results of relevance to the different players are derived for situations with arbitrary numbers of decision alternatives.
In the earlier game theory literature, when general classes of games are analyzed, it has usually not been possible to derive explicit functions. Earlier studies are mostly focused on general principles, proofs of the existence of solutions and numerical algorithms to calculate solutions in particular numerically specified situations.
One of the general results derived and proved in this paper is that, for every game in the TPZSGD class, the optimal strategy, for both players, always leads to a unique and completely mixed strategy Nash equilibrium. This means that, for each player, the optimal frequency of every possible decision, is strictly greater than 0 and strictly less than 1.
This result is critical to analytical TPZSGD game theory. It makes it possible to instantly determine the equation system that should be used to calculate the optimal decision frequences. Hence, the optimal decision frequences become possible to analyze with general analytical methods. Explicit functions can be derived for arbitrary numbers of decision options and for all possible elements in the game matrix. In other words, we do not have to handle every particular case with numerical methods.
In the existing literature on game theory, such a proof is not easily found. This problem is usually avoided by intuitive arguments and reasonable assumptions. The book by Washburn9 is one such example. A similar case is found in Babu et al.12 They avoid to show that the Nash equilibrium, which they analyze, really is completely mixed. Babu et al12 simply assume the existence of a particular probability vector. In this paper, the existence of such a probability vector will be proved for a diagonal game matrix where all diagonal elements are strictly positive. It will also be proved that all elements of the probability vector are strictly positive and strictly less than one. Furthermore, explicit functions will be derived for and the value of the game.
Thanks to the derived functions, it is also possible to perform explicit sensitivity analyses and to determine the directions of changes of optimal decision frequences and expected results if the direction of change of a particular parameter is known.
In this study, it has been possible to derive explicit results in an area that is highly relevant in real applications: How are the optimal decision frequences of the different players changed if the level of risk of some parameter(s) change(s)? Related results have earlier been derived in stochastic dynamic ”one player” problems by Lohmander.14 First, relevant functions of decisions and expected game values are determined. The first and second derivatives are determined and signed. Then, the Jensen inequality is used to determine the directions of change of the optimal decision frequences and expected game values under the influence of increasing risk in the different parameter values.
A TPZSGD will now be analyzed in the most general way. BLUE is the maximizer, who selects the row, i. RED is the minimizer, who selects the column, j. The decision of BLUE is not known by RED before RED takes a decision and the decision of RED is not known by BLUE before BLUE takes the decision. The game matrix, A(i,j), is diagonal. All diagonal elements cij=A(i,j) are strictly positive and represent the reward that BLUE obtains from RED in case i=j. "('The reward that BLUE obtains is equal to the loss that RED gets")". In case i≠j, the reward is zero. Equations (2.1) and (2.2) define these conditions.
cij|i≠j=0,i=1,....,n, j=1,2,..., n (2.1)
cij|i=j=gi>0 , i=1,...,n,j=1,2,...,n (2.2)
A concrete example is the following: RED should move an army convoy from one city to another. One road, among the existing n available roads, should be selected. BLUE wants to destroy as many RED trucks as possible. RED sends the convoy via road j and BLUE moves the equipment and troops to road i and prepares an attack there. If i=j, BLUE attacks RED and destroys the number of RED trucks found in a diagonal element of the game matrix where i=j. . If BLUE and RED select different roads, no attack takes place and no trucks are destroyed. A(i,j)=0 for i≠j .
Different roads usually have different properties with respect to slope, curvature, protection, options to hide close to the road and so on. As a consequence, the values of the diagonal elements of the game matrix, A(i,j)>0 for i=j , are usually not the same for different values of i.
The maximization problem of BLUE
The maximization problem of BLUE is defined here. The expected reward, X0, is the objective function, which is found in (2.1.1). The number of possible decisions is n and the probability of a particular decision, i, is Xi. The total probability can not exceed 1, which is shown in (2.1.2.).gi is defined in (2.2). Since RED can select any decision , j,x0 is constrained via (2.1.3). Furthermore, no probability can be negative, which is seen in (2.1.4).
maxx0 (2.1.1)
s.t.n∑i=1xi≤1 (2.1.2)
x0≤gixi , i=1,...,n (2.1.3)
xi≥0 , i=1,...,n (2.1.4)
Let λi denote dual variables. The following Lagrange function is defined:
L=x0+λ0(1−n∑i=1xi)+n∑i=1λi(gixi−x0) (2.1.5)
The following derivatives will be needed in the proceeding analysis:
dLdλ0=1−n∑i=1xi≥0 (2.1.6)
dLdλi=gixi−x0≥0 , i=1,...,n (2.1.7)
dLdx0=1−n∑i=1λi≤0 (2.1.8)
dLdxi=λigi−λ0≤0 , i=1,...,n (2.1.9)
Karush Kuhn Tucker conditions in general problems
In general problems, we may have different numbers of decision variables and constraints. Furthermore, the elements cij|i≠j are not necessarily zero (Table 1).
λi≥0 ∀i |
dLdλi≥0 ∀i |
λidLdλi=0 ∀i |
xj≥0 ∀j |
dLdxj≤0 ∀j |
xjdLdxj=0 ∀j |
Table 1 Karush Kuhn Tucker conditions in general maximization problems
Particular conditions in problems that satisfy (2.1) and (2.2)
Note that in these problems, i=j in all relevant constraints.
λi≥0 ∀i (2.1.10)
dLdλi≥0 ∀i (2.1.11)
λidLdλi=0 ∀i (2.1.12)
xi≥0 ∀i (2.1.13)
dLdxi≤0 ∀i (2.1.14)
xidLdxi=0 ∀i (2.1.15)
Proof 1: Proof that x0*>0 :
(2.1.2) and (2.1.4) make it feasible to let xi>0 , i=1,...n .
(2.2) says that gi>0 , i=1,2,...,n .
When gixi>0, i=1,...n , (2.1.3) makes it feasible to let .x0>0
(2.1.1) states that we want to maximize x0. Let stars indicate optimal values.
Hence, when optimal decisions are taken, x0=x0*>0 .
Proof 2: Proof that xi*>0 , i=1,...,n :
(2.1.7) says that dLdλi=gixi−x0≥0 , i=1,...,n
Proof 1 states that x0>0 . (2.2) says that gi>0 , i=1,...,n .
xi≥x0gi>0 , i=1,...,n .
Hence, xi=xi*>0 , i=0,...,n .
Proof 3: Proof that λi*, i=0,...,n can be determined from a linear equation system.
(xi>0 , i=0,...,n)∧ (2.1.15) ⇒ {dLdx0=0 ; dLdxi=0 , i=1,...,n} ={(2.1.16) ∧ (2.1.17)} .
dLdx0=1−n∑i=1λi=0 (2.1.16)
dLdxi=λigi−λ0=0 , i=1,...,n (2.1.17)
Proof 4: Proof that λi*>0 , i=0,...,n .
(2.1.16) ⇒ ∃i|i>0,λi>0 .
Hence, at least for one strictly positive value i,λi is strictly greater than zero.
(∃i|i>0,λi>0) ∧ (gi>0 , i=1,...,n) (2.1.17) ⇒ λ0>0 .
λ0>0 (2.1.18)
(2.1.17) ∧(gi>0 , i=1,...,n)∧ (2.1.18)⇒(λi>0 , i=1,...,n)
λi>0 , i=1,...,n (2.1.19)
(2.1.18) ∧ (2.1.19)⇒(λi>0 , i=0,...,n)
λi*>0 , i=0,...,n (2.1.20)
Proof 5: Proof that xi* , i=1,...,n , can be determined from a linear equation system.
(λi>0 , i=0,...,n)∧ (2.1.12)⇒ {dLdλ0=0 ; dLdλi=0 , i=1,...,n}={(2.1.21) ∧ (2.1.22)} .
dLdλ0=1−n∑i=1xi=0 (2.1.21)
dLdλi=gixi−x0=0 , i=1,...,n (2.1.22)
Determination of explicit equations that give all values: xi* , i=0,...,n :
(2.1.22) ⇒ (2.1.23).
xi=x0gi , i=1,...,n (2.1.23)
(2.1.21) ⇒ (2.1.24).
n∑i=1xi=1 (2.1.24)
n∑i=1x0gi=1 (2.1.25)
n∑i=11gi=1x0 (2.1.26)
x0=1n∑i=11gi (2.1.27)
x0*=(n∑i=1gi−1)−1 (2.1.28)
xi*=gi−1(n∑q=1gq−1)−1 , i=1,...,n (2.1.29)
Determination of explicit equations that give all values: λi* , i=0,...,n :
(2.1.17) ⇒ (2.1.30).
λi=λ0gi , i=1,...,n (2.1.30)
(2.1.16) ⇒ (2.1.31)
n∑i=1λi=1 (2.1.31)
n∑i=1λ0gi=1 (2.1.32)
n∑i=11gi=1λ0 (2.1.33)
λ0=1n∑i=11gi (2.1.34)
λ0*=(n∑i=1gi−1)−1 (2.1.35)
λi*=gi−1(n∑q=1gq−1)−1 , i=1,...,n (2.1.36)
Observations:
x0*=λ0*=(n∑i=1gi−1)−1 (2.1.37)
xi*=λi*=gi−1(n∑q=1gq−1)−1 , i=1,...,n (2.1.38)
The minimization problem of RED
We are interested in the solution to miny0 . The objective function is formulated as max(−y0) . The frequences of the different decisions, i are yi .
max (−y0) (2.2.1)
s.t.
n∑i=1yi≥1 (2.2.2)
y0≥giyi , i=1,...,n (2.2.3)
yi≥0 , i=1,...,n (2.2.4)
Proof that y0*>0
(2.2.2) ⇒ (2.2.5).
∃i|1≤i≤n, yi>0 (2.2.5)
gi>0 , i=1,...,n (2.2.6)
(2.2.3) ∧ (2.2.5) ∧ (2.2.6) ⇒ (2.2.7).
y0*≥y0>0 (2.2.7)
Let μi denote dual variables. The following Lagrange function is defined for RED:
L2=−y0+μ0(n∑i=1yi−1)+n∑i=1μi(y0−giyi) (2.2.8)
These derivatives will be needed in the analysis:
dL2dμ0=n∑i=1yi−1 ≥0 (2.2.9)
dL2dμi=y0−giyi ≥0 , i=1,...,n(2.2.10)
dL2dy0=−1+n∑i=1μi ≤0 (2.2.11)
dL2dyi=μ0−μigi≤0 , i=1,...,n(2.2.12)
Proof that yi*>0 , i=0,...,n
According to (2.2.1), we want to maximize −y0 , which implies that we minimize y0 .
(2.2.2)⇒n∑i=1yi≥1
(2.2.4)⇒yi≥0 , i=1,...,n
Let us start from an infeasible point, origo, and move to a feasible point in the way that keeps y0 as low as possible. Initially, let (y1,...,yn)=(0,...,0) . According to (2.2.2), this point is not feasible.
(2.2.3)⇒miny0|yi=0 , i=1,...,n=0 .
Now, we have to move away from the infeasible point (y1,...,yn)=(0,...,0) . We have to reach a point that satisfies n∑i=1yi≥1 without increasing y0 more than necessary. To find a point that satisfies (2.2.2), we have to increase the value of at least one of the yi|i∈{1,...,n} . Select one arbitrary index k|1≤k≤n . To simplify the exposition, we let k=1. According to (2.2.3): If we increase y1 by dy1, increases by g1dy1, as long as dyi=0 , i=2,...,n . Hence, dy0=g1dy1 . Let z = dy0=g1dy1 .
However, when dy1>0 , we may also partly increase yi , i=2,...,n without increasing dy0 above z. This follows from (2.2.3) and (2.2.10). Since we want to satisfy , we want to increase as much as possible, without increasing dyemabove . Hence, we select:
gidyi=z = g1dy1 , i=2,...,n (2.2.13)
dyi=g1gidy1 , i=2,...,n (2.2.14)
(dy1>0)∧(gi>0 , i=1,...,n)⇒dyi>0 , i=2,...,n (2.2.15)
Since we started in origo, we have
yi=dyi+0>0 , i=1,...,n (2.2.16)
We already know that y0*≥y0>0 . Hence,.
yi*>0 , i=0,...,n (2.2.17)
Observation: The following direct method can be used to solve the optimization problem of RED.
First, remember that y0*=dy0*+0=z . We may directly determine the optimal values of yi*>0 , i=0,...,n without using the Lagrange function and KKT conditions, in this way:
n∑i=1yi=((dy1+0)+(dy2+0)...+(dyn+0))=1 (2.2.18)
n∑i=1yi=(y1+y2+...+yn)=1 (2.2.19)
n∑i=1yi=(zg1+(g1g2zg1)+...+(g1gnzg1))=1 (2.2.20)
n∑i=1yi=(zg1+zg2+...+zgn)=1 (2.2.21)
n∑i=1yi=(1g1+1g2+...+1gn)=1z (2.2.22)
n∑i=1gi−1=1z (2.2.23)
y0*=z=(n∑i=1gi−1)−1 (2.2.24)
yi*=gi−1y0*=gi−1(n∑q=1gq−1)−1 , i=1,...,n (2.2.25)
Proof that μi* , i=0,...,n can be solved via a linear equation system and that μi*>0 , i=0,...,n .
Since yi*>0 , i=0,...,n , we may determine that μi*>0 , i=0,...,n via a linear equation system.
(yidL2dyi=0 , i=0,...,n)∧(yi>0 , i=0,...,n)⇒(dL2dyi=0 , i=0,...,n)
dL2dy0=−1+n∑q=1μq=0 (2.2.26)
dL2dyi=μ0−μigi=0 , i=1,...,n (2.2.27)
(2.2.26)⇒ ∃i|1≤i≤n, μi>0 (2.2.28)
(gi>0 , i=1,...,n)∧ (2.2.27) ∧ (2.2.28) ⇒μ0>0 (2.2.29)
(gi>0 , i=1,...,n)∧ (2.2.27) ∧ (2.2.29) ⇒(μi>0 , i=1,...,n) (2.2.30)
(2.2.29) ∧ (2.2.30) ⇒(μi>0 , i=0,...,n) (2.2.31)
Proof that yi* , i=0,...,n can be solved via a linear equation system and that yi*>0 , i=0,...,n .
Since μi*>0 , i=0,...,n , we may determine that yi*>0 , i=0,...,n via a linear equation system.
(μidL2dμi=0 , i=0,...,n)∧(μi>0 , i=0,...,n)⇒(dL2dμi=0 , i=0,...,n)
dL2dμ0=n∑q=1yq−1=0 (2.2.32)
dL2dμi=y0−giyi=0 , i=1,...,n (2.2.33)
(2.2.32)⇒∃i|1≤i≤n, yi>0 (2.2.34)
(gi>0 , i=1,...,n)∧ (2.2.33) ⇒y0>0 (2.2.35)
(gi>0 , i=1,...,n)∧ (2.2.35) ⇒(yi>0 , i=1,...,n) (2.2.36)
(2.2.35) ∧ (2.2.36) ⇒(yi>0 , i=0,...,n) (2.2.37)
Determination of explicit equations that give all values:yi* , i=0,...,n :
(2.2.33)⇒ (2.2.38).
yi=y0gi , i=1,...,n (2.2.38)
(2.2.32) ⇒ (2.2.39).
n∑i=1yi=1 (2.2.39)
n∑i=1y0gi=1 (2.2.40)
n∑i=11gi=1y0 (2.2.41)
y0=1n∑i=11gi (2.2.42)
y0*=(n∑i=1gi−1)−1 (2.2.43)
yi*=gi−1(n∑q=1gq−1)−1 , i=1,...,n (2.2.44)
Determination of explicit equations that give all values:μi* , i=0,...,n :
(2.2.27)⇒ (2.2.45).
μi=μ0gi , i=1,...,n (2.2.45)
(2.2.26) ⇒ (2.2.46)
n∑i=1μi=1 (2.2.46)
n∑i=1μ0gi=1 (2.2.47)
n∑i=11gi=1μ0 (2.2.48)
μ0=1n∑i=11gi (2.2.49)
μ0*=(n∑i=1gi−1)−1 (2.2.50)
μi*=gi−1(n∑q=1gq−1)−1 , i=1,...,n (2.2.51)
Observations:
y0*=μ0*=(n∑i=1gi−1)−1 (2.2.52)
yi*=μi*=gi−1(n∑q=1gq−1)−1 , i=1,...,n (2.2.53)
Generalized Observations:
x0*=λ0*=y0*=μ0*=(n∑i=1gi−1)−1 (2.2.54)
xi*=λi*=yi*=μi*=gi−1(n∑q=1gq−1)−1 , i=1,...,n (2.2.55)
Sensitivity analyses
First, the sensitivity analyses will concern these variables: x0*=λ0*=y0*=μ0* . How do these variables change under the influence of changing elements in the game matrix?
Observation:x0*=λ0*=y0*=μ0*=(n∑i=1gi−1)−1
Proof that dx0*dgi>0 ∧ d2x0*dgi2<0 .
x0*=(n∑i=1gi−1)−1 (2.3.1)
dx0*dgi=(−1)(n∑i=1gi−1)−2(−gi−2) (2.3.2)
dx0*dgi=gi−2(n∑i=1gi−1)−2>0 (2.3.3)
d2x0*dgi2=−2gi−3(n∑i=1gi−1)−2+gi−2(−2)(n∑i=1gi−1)−3(−1)gi−2 (2.3.4)
d2x0*dgi2=−2gi−3(n∑i=1gi−1)−2(1−gi−1(n∑i=1gi−1)−1) (2.3.5)
d2x0*dgi2=−2gi−1(xi*)2(1−xi*) (2.3.6)
(0<xi*<1)∧(gi>0)⇒d2x0*dgi2<0 (2.3.7)
Observation:x0* is a strictly increasing and strictly concave function of each gi. From the Jensen inequality, it follows that increasing risk in gi will reduce the expected value of x0* . Compare Figure 1.
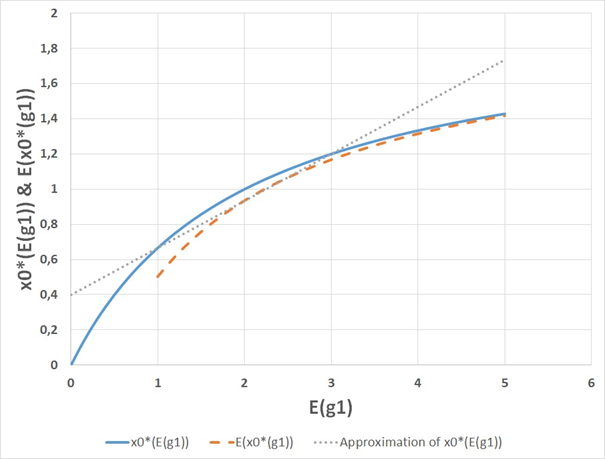
Figure 1 In this graph, the horizontal axes represents E(g1), the expected value of g1. Here, g1 is a stochastic variable. There are two possible outcomes, namely E(g1)−1 and E(g1)+1 , with probabilities ½ and ½ respectively. The vertical axes shows x0*(E(g1)) , the optimal objective function value as a function of the expected value of g1, and E(x0*(g1)) , the expected value of the optimal objective function value of x0* as a function of the value of g1. The graph also includes a linear approximation of x0*(E(g1)) based on the values of x0*(E(g1)) for E(g1)=1 and for E(g1)=3 . This linear approximation is equal to E(x0*(g1)) for E(g1)=2 . According to the Jensen inequality,E(x0*(g1)) < x0*(E(g1)) , when x0*(E(g1)) is a strictly concave function and g1 is a stochastic variable. This graph illustrates that the Jensen inequality is correct. The graph also illustrates the general conclusion that the expected optimal objective function valueE(x0*(g1)) is a strictly decreasing function of the level of risk in g1.
Second, the sensitivity analyses will concern these variables: xi*=λi*=yi*=μi* , i=1,...,n . How do these variables change under the influence of changing elements in the game matrix?
Observation:xi*=λi*=yi*=μi*=gi−1(n∑q=1gq−1)−1 , i=1,...,n
Proof that dxi*dgi<0 ∧ d2xi*dgi2>0 , i∈{1,...,n} .
xi*=gi−1(n∑q=1gq−1)−1 , i=1,...,n (2.3.8)
dxi*dgi=−gi−2(n∑q=1gq−1)−1+gi−1(−1)(n∑q=1gq−1)−2(−gq−2) (2.3.9)
dxi*dgi=gi−2(n∑q=1gq−1)−1(−1+gi−1(n∑q=1gq−1)−1) (2.3.10)
dxi*dgi=gi−1xi*(−1+xi*) (2.3.11)
(gi>0)∧(0<xi*<1)⇒dxi*dgi<0 (2.3.12)
d2xi*dgi2= −gi−2xi*(xi*−1) + gi−1(gi−1xi*(xi*−1))(xi*−1) + gi−1xi*gi−1xi*(xi*−1) (2.3.13)
d2xi*dgi2= −gi−2(xi*(xi*−1) − (xi*(xi*−1))(xi*−1) − xi*xi*(xi*−1)) (2.3.14)
d2xi*dgi2= −gi−2((xi*)2−xi*−xi*((xi*)2−2xi*+1)−(xi*)2(xi*−1)) (2.3.15)
d2xi*dgi2= −gi−2((xi*)2−xi*−(xi*)3+2(xi*)2−xi*−(xi*)3+(xi*)2) (2.3.16)
d2xi*dgi2= −gi−2(−2(xi*)3+4(xi*)2−2xi*) (2.3.17)
d2xi*dgi2= 2gi−2xi*((xi*)2−2xi*+1) (2.3.18)
d2xi*dgi2= 2gi−2xi*(xi*−1)2 (2.3.19)
(gi≠0)∧(0<xi*<1)⇒d2xi*dgi2>0 (2.3.20)
Observation:xi* is a strictly decreasing and strictly convex function of gi. From the Jensen inequality, it follows that increasing risk in gi will increase the expected value of xi* . Compare Figure 2.
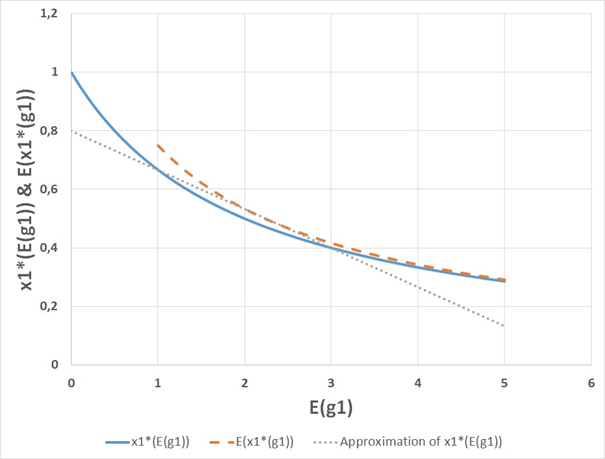
Figure 2 In this graph, the horizontal axes represents E(g1) , the expected value of g1. Here, g1 is a stochastic variable. There are two possible outcomes, namely E(g1)−1 and E(g1)+1 , with probabilities ½ and ½ respectively. The vertical axes shows the optimal decision frequency x1*(E(g1)) as a function of the expected value of g1, and E(x1*(g1)) , the expected value of the optimal frequency x1* as a function of the value of . The graph also includes a linear approximation of x1*(E(g1)) based on the values of x1*(E(g1)) for E(g1)=1 and for E(g1)=3 . This linear approximation is equal to E(x1*(g1)) for E(g1)=2 . According to the Jensen inequality, E(x1*(g1))>x1*(E(g1)) , when x1*(E(g1)) is a strictly convex function and g1 is a stochastic variable. This graph illustrates that the Jensen inequality is correct. The graph also illustrates the general conclusion that the expected optimal decision frequency E(x1*(g1)) is a strictly increasing function of the level of risk in g1.
Proof that dxk*dgi>0 ∧ d2xk*dgi2<0 , i∈{1,...,n},k∈{1,...,n},i≠k .
xk*=gk−1(n∑i=1gi−1)−1 (2.3.21)
dxk*dgi|i≠k=gk−1(−1)(n∑i=1gi−1)−2(−gi−2) (2.3.22)
dxk*dgi|i≠k=gk−1gi−2(n∑i=1gi−1)−2 (2.3.23)
(gm>0 , m=1...,n))⇒dxk*dgi|i≠k>0 (2.3.24)
d2xk*dgi|i≠k2=gk−1(−2gi−3(n∑i=1gi−1)−2+gi−2(−2)(n∑i=1gi−1)−3(−gi−2)) (2.3.25)
d2xk*dgi|i≠k2=2gk−1gi−3(n∑i=1gi−1)−2((gi−1)(n∑i=1gi−1)−1−1) (2.3.26)
d2xk*dgi|i≠k2=2gk−1gi−1(xi*)2(xi*−1) (2.3.27)
(gm>0 , m=1,...,n)∧(0<xi*<1)⇒d2xk*dgi|i≠k2<0 (2.3.28)
Observation:xk* is a strictly increasing and strictly concave function of gi. From the Jensen inequality, it follows that increasing risk in gi will decrease the expected value of xk* . Compare Figure 3.
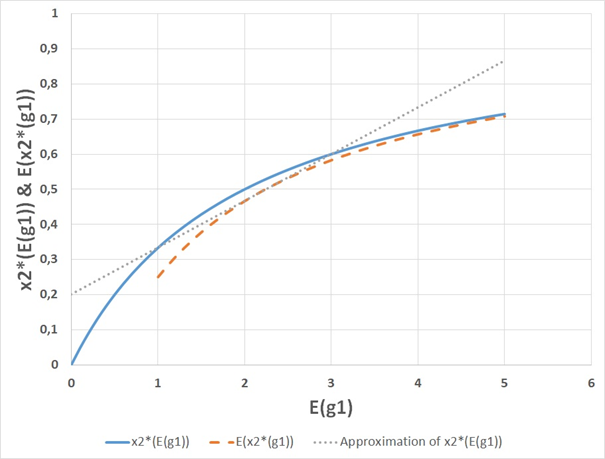
Figure 3 In this graph, the horizontal axes represents E(g1) , the expected value of g1. Here, g1 is a stochastic variable. There are two possible outcomes, namely E(g1)−1 and E(g1)+1 , with probabilities ½ and ½ respectively. The vertical axes shows the optimal decision frequency x2*(E(g1)) as a function of the expected value of g1, and E(x2*(g1)) , the expected value of the optimal frequency x2* as a function of the value of g1. The graph also includes a linear approximation of x2*(E(g1)) based on the values of x2*(E(g1)) for E(g1)=1 and for E(g1)=3 . This linear approximation is equal to E(x2*(g1)) for E(g1)=2 . According to the Jensen inequality, E(x2*(g1))<x2*(E(g1)) , when x2*(E(g1)) is a strictly concave function and g1 is a stochastic variable. This graph illustrates that the Jensen inequality is correct. The graph also illustrates the general conclusion that the expected optimal decision frequency E(x2*(g1)) is a strictly decreasing function of the level of risk in g1.
The general definition of the following illustrating game is given in the preceeding section. Let n=2. A very detailed background and interpretation of this particular game, without the new functions and proofs, is given in Lohmander (2019).14
A=[g100g2]=[2003] (3.1)
From (2.2.54) we know that:
x0*=λ0*=y0*=μ0*=(n∑i=1gi−1)−1 (3.2)
x0* , the expected reward of BLUE, is equal to y0* , the expected loss of RED, in case both optimize the respective strategies. Using the numerical values of the elements in A, we get:
x0*=112+13=65=1.2 (3.3)
Hence, the expected value of the game is 1.2. This value is also shown in Figure 4. and Figure 5. The expected value of the game is a decreasing function of the level of risk of , which is described in connection to, and illustrated in, Figure 1.
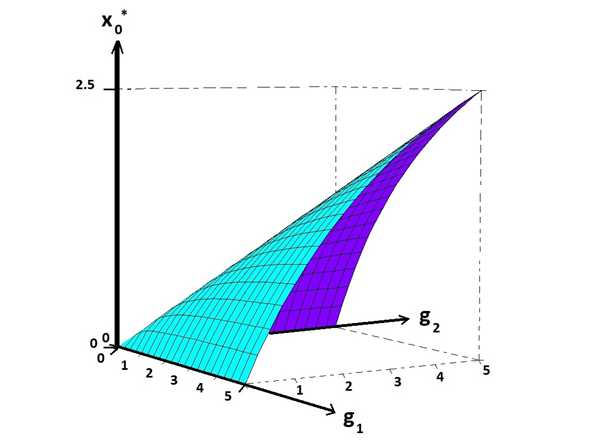
Figure 4 The objective function value x0* as a function of the two parameters (g1,g2) .x0* is a strictly increasing function of both parameters.
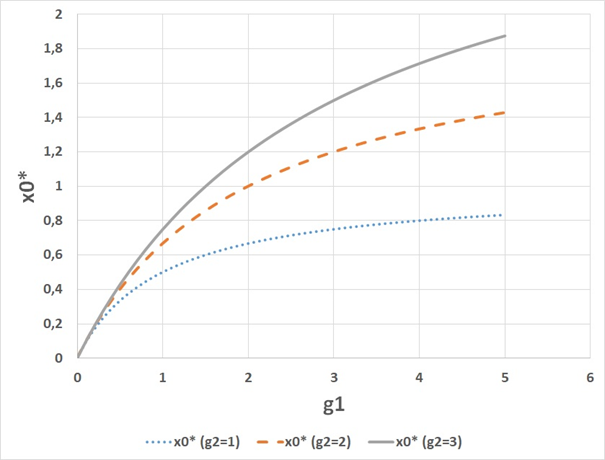
Figure 5 The optimal objective function value x0* as a function of the parameter g1 for alternative values of g2.x0* is a strictly increasing and strictly concave function of g1. Furthermore,x0* is an increasing function of g2.
From (2.2.55) we know that:
xi*=λi*=yi*=μi*=gi−1(n∑q=1gq−1)−1 , i=1,...,n (3.4)
For BLUE and RED, the optimal probabilities to select different roads are equal. For BLUE, the optimal probability to select road 1 is x1* . Via the elements in, we get:
x1*=y1*=(12)x0*=0.6 (3.5)
x2*=y2*=(13)x0*=0.4 (3.6)
x1* is shown in Figures 6 & 7. In Figure 8, the optimal value is illustrated. The expected value of x1* is an increasing function of the level of risk in g1, which is shown in Figure 2. For BLUE, the optimal probability to select road 2, is x2* . In Figure 9, we find this value is 0.4. Figure 3 illustrates that the expected value of x2* is a decreasing function of the level of risk in g1.
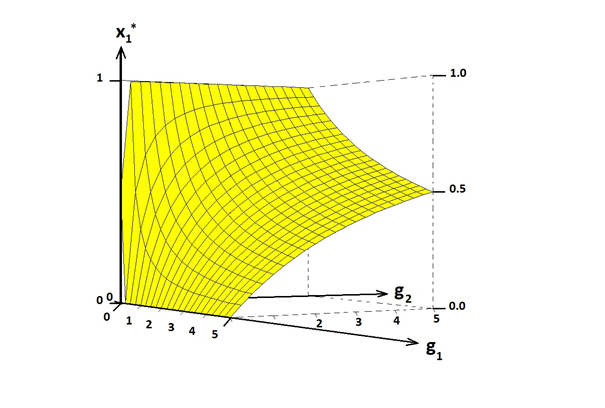
Figure 6 The optimal decision frequency x1* , as a function of the two parameters (g1,g2).x1* is a strictly decreasing and strictly convex function of g1.x1* is a strictly increasing and strictly concave function of.g2
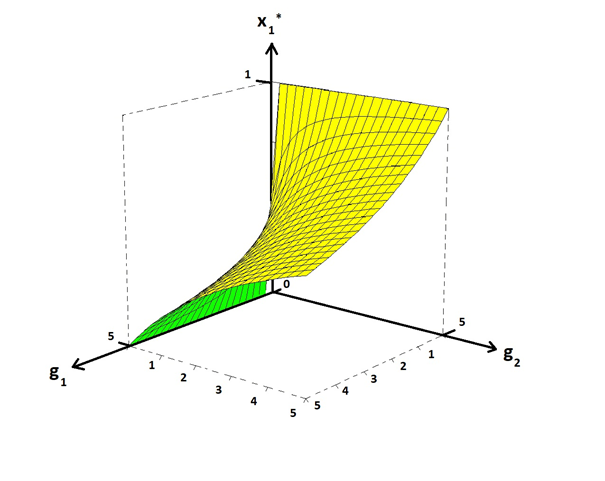
Figure 7 The optimal decision frequency x1* , as a function of the two parameters (g1,g2).x1* is a strictly decreasing and strictly convex function of g1.x1* is a strictly increasing and strictly concave function of g2. Compare Figure 4., which shows the function from another angle.
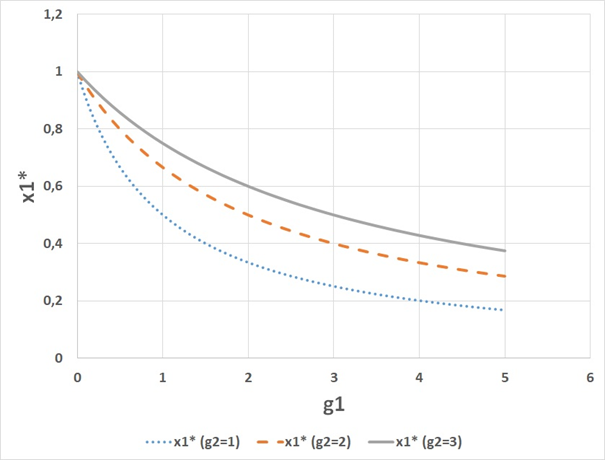
Figure 8 The optimal decision frequency x1* as a function of the parameter g1 for alternative values of g2.x1* is a strictly decreasing and strictly convex function of g1. Furthermore,x1* is an increasing function of g2.
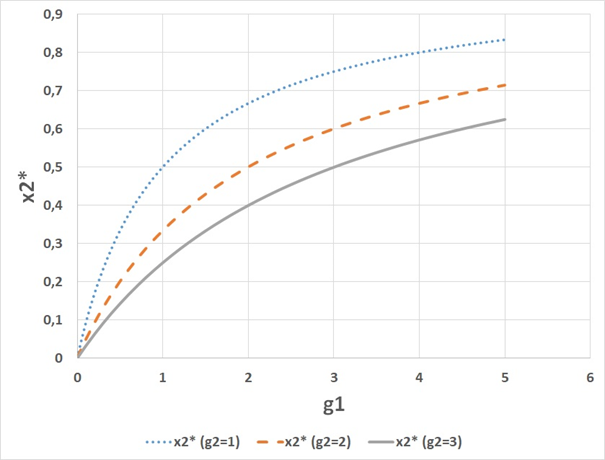
Figure 9 The optimal decision frequency x2* as a function of the parameter g1 for alternative values of g2.x2* is a strictly increasing and strictly concave function of g1. Furthermore,x2* is an decreasing function of g2.
The particular results (x0*,x1*,x2*) discussed in this in this section were also obtained by Lohmander (2019)14 via the traditional game theory approach of linear programming.
In this paper, the two player zero sum games with diagonal game matrixes, TPZSGD, are analyzed. Many important applications of this particular class of games are found in military decision problems, in customs and immigration strategies and police work. Explicit functions are derived that give the optimal frequences of different decisions and the expected results of relevance to the different decision makers. Arbitrary numbers of decision alternatives are covered. It is proved that the derived optimal decision frequency formulas correspond to the unique optimization results of the two players. It is proved that the optimal solutions, for both players, always lead to a unique completely mixed strategy Nash equilibrium. For each player, the optimal frequency of a particular decision is strictly greater than 0 and strictly less than 1. With comparative statics analyses, the directions of the changes of optimal decision frequences and expected game values as functions of changes in different parameter values, are determined. Some of the derived formulas are used to confirm earlier game theory results presented in the literature. It is demonstrated that the new functions can be applied to solve a typical military decision problem and that the new functions make it possible to draw clear conclusions concerning issues that were not earlier possible to get via linear programming solutions. With the new approach developed here, it is possible to determine the directions of change of the expected value of the objective function and of the optimal frequences of the different decision alternatives, under the influence of increasing risk in the game matrix elements. Such game matrix elements are in real applications never known with certainty. Hence, this new approach leads to more relevant results than those that can be obtained with earlier methods.
None.
None.
The author declares that there was no conflicts of interest.

©2019 Lohmander. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.