This paper presents a position control problem for an under actuated overhead crane system, which has two degrees of freedom with only one actuator for trolley driving. An overhead crane transfers a work piece to a desired position while keeping the swing angle of the work piece small during this process. The rope should not have a swing angle at the load destination. In this paper, five controllers (i.e., linear and nonlinear controllers) are derived based on the passivity of the system. The total energy of the system and its square are used in a Lyapunov candidate function to design the controllers. The equilibrium point of the closed loop is proven asymptotically stable by the Lyapunov technique and LaSalle invariance theorem. The optimal linear controller is combined to force the swing angle to converge rapidly to zero by reaching the trolley location. Numerical simulations and experiments are conducted by using the test bed model to evaluate the controllers.

Keywords: under actuated nonlinear systems, overhead crane, energy-based control

Industries and services such as heavy industry, construction work, loading/unloading the harbor and automotive industries widely use overhead cranes. The main purpose of the overhead crane is to transport the heavy workpiece to the target position. However, the swing of the processed object must be eliminated at the target position for better performance and productivity. To increase the productivity of the overhead crane, fast accelerated and decelerated operations are required. However, fast acceleration and deceleration motions create a dangerous situation by shaking the workpiece suspended from the hoist. If heavy workloads are shaken too much, the facilities and infrastructure around the overhead crane can be destroyed or, in severe cases, the crane itself can be broken and may cause people to suffer serious injuries. The most important part of crane work is horizontal transport, which moves the workpiece horizontally to the goal position after lifting it. In this horizontal motion task, the trolley and workpiece must reach the desired goal position quickly while keeping a small swing angle. When the trolley reaches the target position, the swing angle is suppressed to zero. The following two main approaches are necessary to reach the above-mentioned requirement. The first one consists of designing a proper trajectory for the trolley (i.e., motion planning). The second approach involves designing an anti-swing controller (i.e., control design). In the first approach, the reference trajectory of the overhead crane has a general motion control velocity profile. That is, it is composed of three stages of acceleration, constant velocity, and deceleration. The accelerating and decelerating time and shape in the first and third phases increase the swing angle to its maximum value before decreasing the angle to zero. Consequently, the swing angle is zero in the constant velocity phase.¹

The second approach has attracted the interest of researchers. Numerous control methods have also been studied for overhead cranes. Several controllers can be listed as linear, gain schedule, nonlinear, partial feedback linearization, sliding mode, adaptive, fuzzy logic, and so on.^2–12 Each controller has its own advantages and disadvantages, the details of which can be found.¹³ A combination of control methods is considered by several authors (e.g., adaptive and adaptive fuzzy sliding-mode controls).^14–19 These combinations produce complex controllers with parameters that do not guarantee system stability. Design methods based on the energy and passivity of the system has been studied. This control approach can be applied not only to fully actuated systems, but also to under-operating systems such as under-operated actuators,^20,21 overhead cranes,⁴ and ball-beam systems.²² The aforementioned method exhibits simplicity in designing a controller from energy-storage function, which adopts mechanical, kinetic, and potential energies. The additional energy affects the control performance. Based on the aforementioned studies, we utilize passivity to generalize the controller design for under actuated overhead crane systems. Five controllers, including linear and nonlinear controllers, are designed based on the total energy of an overhead crane. The Lyapunov candidate function is chosen by a combination of the system energy and the kinetic and potential energies. The origin of the closed-loop system is proven asymptotically stable by the Lyapunov technique and LaSalle invariance theorem. Energy-based controllers guarantee the asymptotic stability of the system; however, the choice of control parameters is an ad hoc issue. Another disadvantage of these controllers is that the swing angle converges slowly to zero. Therefore, the linear optimal controller in this study is switched on when the trolley reaches a point close to the destination. The system response is significantly improved by applying this technique. The remainder of this paper is organized as follows. Section 2 introduces the nonlinear dynamics of an overhead crane with two degrees of freedom (DOFs), as well as the useful properties of a dynamic system. Sections 3 presents an energy-based control design in which five controllers based on Lyapunov theory are derived. Section 4 shows the numerical and experimental verifications of the controllers. Section 5 concludes.

Dynamic model

The control problem of the crane during the horizontal transportation phase is addressed in this section. The rope has constant length, and the system has two DOFs. The following assumptions are established to obtain the dynamic model of the system:

1. the payload is considered a point mass;
2. the mass and stiffness of the hoisting rope are neglected;
3. the effects of wind disturbances are not considered. Based on the Lagrangian formulation,^{23 the dynamic model of a 2D overhead crane system is represented by the following:}

 $M(q)\ddot{q}+C(q,\dot{q})\dot{q}+D\dot{q}+g(q)=Bu$,           (1)

Where $q={[x,\theta ]}^T$denotes the system state vector with $x(t)$ as the trolley displacement and $\theta (t)$as the payload swing angle (Figure 1). $M(q),C(q,\dot{q}),$$D,$$g(q)$,$B$, and $u$ represent the inertia matrix, centripetal-Coriolis matrix, damping matrix, a term derived from potential energy, input control matrix, and force acting on the trolley, respectively. These variables are explicitly defined as follows:

$M(q)=\left[\begin{array}{cc}{m}_t+m_p& m_{p}lcos\theta \\ m_{p}lcos\theta & m_p{l}^2\end{array}\right]=M^T(q)$,

$C(q,\dot{q})=\left[\begin{array}{cc}0& -m_{p}l\dot{\theta }sin\theta \\ 0& 0\end{array}\right]$, $g(q)={\left[\begin{array}{cc}0& m_{p}glsin\theta \end{array}\right]}^T$,

$D=\left[\begin{array}{cc}{d}_x& 0\\ 0& 0\end{array}\right],B=\left[\begin{array}{c}1\\ 0\end{array}\right]$,

where$m_t$and$m_p$represent the trolley mass and payload mass, respectively; $l$denotes the length of the rope;$g$is the gravitational acceleration;$d_x$is the damping coefficient on the trolley,$d_x>0$. The force$u_c$summarizes the actuating forces $f_r$ and coulomb forces$f_r$as the following:

$u=u_c-f_r$ (2)

Figure 1 Overhead crane model.

The coulomb friction in this study is modeled by the tanh function instead of the sign function:

$f_r=f_0\tanh (c\dot{x}),c>>1$,

where $f_0$ is the magnitude of the coulomb friction on the trolley.

Eq. (1) can be rewritten as follows:

$(m_t+m_p)\ddot{x}+m_{p}l\cos \theta \ddot{\theta }-m_{p}l{\dot{\theta }}^2\sin \theta +d_x\dot{x}=u$,     (3)

$m_{p}l\cos \theta \ddot{x}+m_p{l}^2\ddot{\theta }+m_{p}gl\sin \theta =0$.       (4)

By solving $\ddot{\theta }$ from Eq. (4) and integrating this variable into Eq. (3), we obtain the following:

${\overline{m}}_{11}\ddot{x}+d_x\dot{x}+{\overline{h}}_1(q,\dot{q})=u$,          (5)

$l\ddot{\theta }+g\sin \theta =-\ddot{x}\cos \theta$,             (6)

with  ${\overline{m}}_{11}=[m_t+m_p{\sin }^2\theta ],$
$${\overline{h}}_1=-m_p\sin \theta (l{\dot{\theta }}^2+g\cos \theta )$$. (7)

The following assumptions are made from the practical application of an overhead crane: i) the cable length is always positive (i.e., $l>0$), and ii) the swing angle of the payload during the transportation process always remains in the interval between $-\frac{1}{2}\pi$ and $\frac{1}{2}\pi$, [$-\frac{1}{2}\pi <\theta <\frac{1}{2}\pi$]. The dynamic expression in Eq. (1) has the following important properties: (i) the inertia matrix is positive definite and symmetric, $M=M^T>0$; (ii) the matrix $N=(\dot{M}-2C)$ is skew symmetric, $s^T(\dot{M}-2C)s=0$ for $\forall s\in {\Re }^2$.

Open-loop system passivity

Consider that the energy-storage function$E$consists of the kinetic and potential energies of the system:

$E(q,\dot{q})=\frac{1}{2}{\dot{q}}^{T}M(q)\dot{q}+P(q)$,     (8)

With $P(q)=m_{p}gl(1-\cos \theta )\ge 0.$

The energy-storage function derivative regarding time is calculated as follows:

$\dot{E}={\dot{q}}^{T}M(q)\ddot{q}+\frac{1}{2}{\dot{q}}^T\dot{M}(q)\dot{q}+{\dot{q}}^{T}g(q).$  (9)

Substituting the term $M(q)\ddot{q}$ from Eq. (1) and using the skew-symmetric property of$\frac{1}{2}\dot{M}(q)-C(q,\dot{q})$ produces the following:

$\dot{E}=-d_x{\dot{x}}^2+\dot{x}u\le \dot{x}u$  (10)

The term $\dot{x}u$ denotes the power supplied by the actuators for the trolley. The inequality in Eq. (10) shows that the system is passive. Integrating both sides from zero to$t$yields the following:

$E(t)-E(0)={\displaystyle {\int }_0^t\dot{E}ds}=-{\displaystyle {\int }_0^t{d}_x{\dot{x}}^{2}ds}+{\displaystyle {\int }_0^t\dot{x}uds}\le {\displaystyle {\int }_0^t\dot{x}uds}$

or$E(t)-E(0)\le {\displaystyle {\int }_0^t\dot{x}uds}$. In case of a zero input, that is, $u=0,$ the system will have a stable equilibrium$(x,\theta ,\dot{x},\dot{\theta })$$=(x_d,0,0,0)$, where the total energy is minimized after taking the zero value.

Energy-based control design

The control design aims to bring the trolley from an initial condition to a desired position while the payload swing angle is suppressed and vanishes completely at the load destination. This objective indicates that the state variables $q={[x,\theta ]}^T$should reach their desired values$q_d={[x_d,0]}^T$after a short time. The force$u$is derived initially by using an energy-based approach. The friction force is then added to obtain the actuating forces from Eq (2):

$u_c=u+f_r$  (11)

Controller design

The passivity property of the system allows us to exploit the energy of the system, $E$or$E^2$, in the controller design. The following Lyapunov candidate function is proposed:

$V=\frac{1}{i}{k}_E{E}^i(q,\dot{q})+\frac{1}{2}{k}_v(q){\dot{x}}^2+\frac{1}{2}{k}_p{\tilde{x}}^2$,     (12)

Where$i$can take the values of one or two, $k_p>0,$ $k_v(q)\ge 0$, and $\tilde{x}=x-x_d.$The second and third terms in$V$are considered additional kinetic and potential energies that are related to the motion of the actuated coordinates, respectively. By differentiating$V$with respect to time, one obtains the following:

$\dot{V}=k_E{E}^{i-1}\dot{E}(q,\dot{q})+\dot{x}{k}_v(q)\ddot{x}+\frac{1}{2}{\dot{k}}_v(q){\dot{x}}^2+\dot{x}{k}_p\tilde{x}$.      (13)

By substituting Eq. (10) into Eq. (13) and accounting for Eq. (5), the following is obtained:

$\dot{V}=\dot{x}\left[\left(k_E{E}^{i-1}+k_v{\overline{m}}_{11}^{-1}\right)u-k_v{\overline{m}}_{11}^{-1}{\overline{h}}_1+\frac{1}{2}{\dot{k}}_v\dot{x}+k_p\tilde{x}\right]-\left(k_E{E}^{i-1}+k_v{\overline{m}}_{11}^{-1}\right)d_x{\dot{x}}^2.$    (14)  

Eq. (14) suggests choosing the following control law:

$u=\frac{\left(-k_d\dot{x}-k_p\tilde{x}+k_v{\overline{m}}_{11}^{-1}{\overline{h}}_1-\frac{1}{2}{\dot{k}}_v\dot{x}\right)}{\left(k_E{E}^{i-1}+k_v{\overline{m}}_{11}^{-1}\right)}={\left(k_E{E}^{i-1}+k_v{\overline{m}}_{11}^{-1}\right)}^{-1}\left(u_{pd}+u_{nl}\right),$,        (15)

with$k_d>0$,

$u_{pd}=-k_d\dot{x}-k_p\tilde{x}$,     (16)

$u_{nl}=k_v{\overline{m}}_{11}^{-1}{\overline{h}}_1-\frac{1}{2}{\dot{k}}_v\dot{x}$.       (17)

By defining the controller via Eqs. (15) to (17), the derivative$\dot{V}$becomes the following:

$\dot{V}=-k_d{\dot{x}}^2-\left(k_E{E}^{i-1}+k_v{\overline{m}}_{11}^{-1}\right)d_x{\dot{x}}^2\le 0$.    (18)

The variable $u_{pd}$ is independent of$k_v$, whereas $u_{nl}$ is dependent on not only $k_v$ but also its derivative ${\dot{k}}_v$ (Eq. (17)). The parameter$i$appears only in one term in Eq. (15). The system energy $E$ appears in the controller (Eq. (15)) only if $i=2$ because $i=1$ leads to $E^0=1$.

The parameter$k_v$can be chosen arbitrarily provided that it is non-negative, thus leading to$k_v{\overline{m}}_{11}^{-1}{d}_x\ge 0$. The three cases for these choices are as follows:$k_v=0$; $k_v=\mathrm{const}\ne 0$; $k_v=\alpha {\overline{m}}_{11}(q),$with $\alpha \ge 0$. The part $u_{nl}$ in Eq. (17) that corresponds with the chosen $k_v$ is expressed as follows:

$k_v=0\Rightarrow u_{nl}=0$,        (19)

$k_v=\mathrm{const}\Rightarrow u_{nl}=k_v{\overline{m}}_{11}^{-1}{\overline{h}}_1-\frac{1}{2}{\dot{k}}_v\dot{x}$,           (20)

$k_v=\alpha {\overline{m}}_{11}(q),\alpha >0\Rightarrow u_{nl}=\alpha \left({\overline{h}}_1-\frac{1}{2}{\dot{\overline{m}}}_{11}\dot{x}\right)$.              (21)

The term in Eq. (21)s written in detail as follows:

$u_{nl}=-\alpha m_p(l{\dot{\theta }}^2+g\cos \theta +\dot{x}\dot{\theta }\cos \theta )\sin \theta$.

The five controllers obtained from Eqs. (15) and (17) by the combination of $i=1,2$ and the three cases of $k_v$ are presented in the following.

Controller 1. The simplest case is produced by $i=1$ and $k_v=0$. For this case, Eq. (15) becomes a proportional-derivative (PD) controller.

$u_1=k_E^{-1}{u}_{pd}=-k_E^{-1}\left(k_d\dot{x}+k_p\tilde{x}\right)$. (22)

Controller 2. By choosing $i=1$, $k_v=\mathrm{const}\ne 0,$ and ${\dot{k}}_v=0$, one obtains the following:

$u_2={(k_E+k_v{\overline{m}}_{11}^{-1})}^{-1}\left(u_{pd}+u_{nl}\right)$,       (23)

where    $u_{pd}$ is defined in Eq. (16), and $u_{nl}$ is defined in Eq. (20).

Controller 3. By choosing $i=2$, $k_v=\mathrm{const}\ne 0$, and ${\dot{k}}_v=0$,

$u_3={(k_{E}E+k_v{\overline{m}}_{11}^{-1})}^{-1}\left(u_{pd}+u_{nl}\right)$,      (24)

where  $u_{pd}$ is defined in Eq. (16), and $u_{nl}$ is defined in Eq. (20).

Controller 4. By choosing $i=1$ and $k_v=\alpha {\overline{m}}_{11}(q)$,

$u_4={(k_E+\alpha )}^{-1}\left(u_{pd}+u_{nl}\right)$,        (25)

where $u_{pd}$ is defined in Eq. (16), and $u_{nl}$ is defined in Eq. (21).

Controller 5. By choosing $i=2$ and $k_v=\alpha {\overline{m}}_{11}(q)$,

$u_5={(k_{E}E+\alpha )}^{-1}\left(u_{pd}+u_{nl}\right)$,     (26)

where $u_{pd}$ is defined in Eq. (16), and $u_{nl}$ is defined in Eq. (21).

Remarks:
1) The controller in Eq. (22) is the simplest and does not require the swing angle and swing angle derivative for feedback. Other controllers require swing-angle sensors.
2) The controllers in Eqs. (24) and (26) require a longer time than the controllers in Eqs. (23) and (25) in calculating the total energy E of the system.
3) The term $k_d$ can be chosen as a function of $\dot{\theta }$ provided that $k_d$is positive and definite. For example, in the case of the PD controller, one can write the following:

$$u_{pd}=-k_p\tilde{x}-[k_d({\dot{\theta }}^2)]\dot{x}$$.            (27)

Stability analysis

Theorem 1. The system in Eq. (1) with one of the controllers from Eqs. (22) to (26) are asymptotically stable at the equilibrium point:

$(q,\dot{q})=(x_d,0,0,0)$.   (28)

Proof. The stability analysis of all five controllers is almost similar; thus, only the stability of the controller in Eq. (25) is proven. The proof of the stability of the equilibrium point or the desired position is based on LaSalle invariance theorem (e.g., see24). From Eq. (18), the invariant set W can be defined as follows:

$\Omega =\{(q,\dot{q}):\dot{x}=0\}$. [${\dot{V}}_1=0$in W].

This expression denotes that$x=\mathrm{const}$, $\theta ,\dot{\theta }$ can take any values, the constant $\tilde{x}$ in W is the equilibrium point$x=x_d$, and$\theta =0,$$\dot{\theta }=0$. The proof is obtained by contradiction. Assuming that$x\ne x_d$, that is, these variables have constant values that are different from the equilibrium, and by considering the control law in Eq. (25), the following expression is obtained:

$u=\frac{1}{(k_E+k_v)}\left(-k_p\tilde{x}-k_v{m}_p(l{\dot{\theta }}^2+g\cos \theta )\sin \theta \right)$.      (29)

Eq. (5) with $\ddot{x}=0$ deduces the condition for  as ${\overline{h}}_1(q,\dot{q})=u$:

$-m_p(l{\dot{\theta }}^2+g\cos \theta )\sin \theta =\frac{1}{(k_E+k_v)}\left(-k_p\tilde{x}-k_v{m}_p(l{\dot{\theta }}^2+g\cos \theta )\sin \theta \right).$

After simplifying the aforementioned equation, we obtain the following:

$k_E{m}_p(l{\dot{\theta }}^2+g\cos \theta )\sin \theta =k_p\tilde{x}=\mathrm{const}$.   (30)

From Eq. (6), we obtain the following in W:

$l\ddot{\theta }+g\sin \theta =0$.        (31)

From Eq. (31), if $\theta \ne 0$ or $\dot{\theta }\ne 0$, then $l=\mathrm{const}$ in W yields the following;

$\frac{1}{2}l{\dot{\theta }}^2+g(1-\cos \theta )=\gamma =\mathrm{const}$. (32)

1) If $\gamma =0\Rightarrow \dot{\theta }=0,\theta =0$, then $\tilde{x}=0$ from Eq. (30) causes $u=0$ from Eq. (29)$u=0$.
2) If $\gamma \ne 0$, taking $l{\dot{\theta }}^2$ from Eq. (32) then placing it into Eq. (30) obtains the following:

$k_E{m}_p\left[2\gamma -2g+3g\cos \theta \right]\sin \theta =k_p\tilde{x}=\mathrm{const}$,
or
$(2\gamma -2g+3g\cos \theta )\sin \theta =\mathrm{const}$.            (33)

From (33), $\theta =\phi =\mathrm{const}$. This constant $\phi$ must be zero because $\phi =\mathrm{const}\ne 0$ leads to $\ddot{\theta }\ne 0$ in Eq. (31). This case leads to$\dot{\theta }(t),\theta (t)\ne \mathrm{const}$. However, $\theta =\phi =0$ leads to $\gamma =0$$\gamma =0$; hence, the assumption that $\gamma \ne 0$ is invalid. Based on the previous analysis, the largest invariant set W includes only the equilibrium point of

$x,\theta ,\dot{x},\dot{\theta }{]}^T={[x_d,0,0,0]}^T$.

We conclude that the system states asymptotically converge to the desired values by invoking LaSalle invariance theorem.²⁴

Numerical simulations and experiments

Numerical simulations are conducted by using MATLAB software to verify the validity and efficiency of the five controllers. Experiments are also conducted by using an overhead crane test bed to validate the control approach. The control objective of the overhead crane is to move the trolley to its destination while complementing the load anti-swing.

Numerical simulations

In the simulation, the system parameters are set as follows: $m_t=2kg$, $m_p=0.85kg$, $d_x=20$Ns/m, $l=0.7$m, and $g=9.81m/s^2$. The target position of the trolley is set as $x_d=0.5m$ m. The controllers in Eqs. (22) to (26) are implemented in the simulation. The parameters of these controllers are chosen as follows:

$k_E=1$, $k_v=2$, $\alpha =1$, $k_p=20,$ $k_d=40$.

In the simulations, the fourth-order Runge–Kutta method with a time step of 0.01s is applied. The simulation results for the trolley displacement, load swing angle, and control input are shown in Figure 2-4. The simulation results show that the energy control scheme controls the trolley to reach the desired destination while implementing anti-sway control. In all cases, the desired positions of the trolley and payload are reached after approximately 15s to 18s. During this time, the payload swing angle increases from zero at the starting time and damped oscillation. The maximum swing angle is approximately 4°. In addition to the maximum swing angle${\theta }_{\max }$, the settling time $t_s,$ maximum control forces$u_{\max }$, and “energy consumption” (defined by $I={\int }_0^{20}{u}^{2}dt$) are considered in comparing controller performances. The performance indices of each case are presented in Table 1.

Figure 2 Trolley displacements.

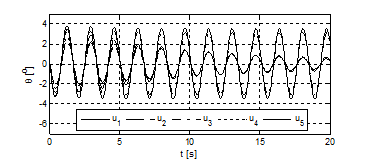
Figure 3 Cable swing angle.

Figure 4 Trolley moving force.

Remarks:

1. The swing angle caused by the controllers in Eqs. (24) and (26) are relatively larger than that by other cases. The swing angle decreases slowly. These two controllers are derived from the square of the system energy$E^2$$E^2$, whereas the controllers in Eqs. (22), (23), and (25) are derived from$E^1$. The swing angles by the controllers derived from $E^2$ decrease significantly faster than those by controllers derived from.
2. Table 1 shows that the swing angle and energy consumption of the controllers in Eqs. (23) and (25) are smaller than those of other controllers. However, the settling time of the trolley from the controllers in Eqs. (23) and (25) is longer than that from other controllers.
3. The simulation results show that the trolley position is reached. However, the swing angle is still vibrating and decreasing slowly.
4. The choice of control parameters, namely, $k_E,k_v,\alpha ,k_p,$ and$k_d$, is an ad hoc problem. The choice of optimal parameters for the controllers is not addressed in this paper.

The controllers based on the energy approach guarantees that the system reaches the desired position. However, choosing the control parameters is not easy, and the swing angle is still large when the trolley reaches its desired position. To overcome this difficulty, a linear state feedback controller is applied in conjunction with the controllers in Eq. (15). The linear state feedback controller is designed based on the linearized model of the system around the desired position. The linearized model is determined to be controllable. Thus, the pole placement technique or linear quadratic regulator (LQR) can be applied to determine the feedback gain matrix, K.²⁵ The command control is then defined as follows:

$u_6=-K(x-x_d)$(34)

Where $x={\text{[}{q}^T,{\dot{q}}^T\text{]}}^T,$ $x_d={\text{[}{x}_d,0,0,0\text{]}}^T$.

The linearized model around the desired position is given as follows:

$\dot{x}=Ax+Bu,$

Matrices $Q$ and $R$ are chosen to obtain the feedback gain:

$Q=100\mathrm{diag}(1,1,1,1),R=1$,

The matrix K is given by the LQR command in MATLAB as the following:

$K=\left[\begin{array}{cccc}10& -28.75& 4.819& -3.73\end{array}\right]$.

The aforementioned nonlinear controllers in Eqs. (22) to (26) guarantee the stability of the desired position; thus, the state variable $q_2=\theta$ and $\dot{q}$ are small around the end position. Therefore, the stability of the closed-loop system is still guaranteed by switching from the nonlinear controllers to the LQR controller in Eq. (34). In the following simulation, the LQR controller is switched on when the trolley reaches 80% of its path. The simulation results by the combination of nonlinear (25) [$u_4$] and linear controllers (34) [$u_6$], as well as (26) [$u_5$] and (34) [$u_6$], are shown in Figure 5-7. Figure 5 shows that the time history of the trolley displacement is not changed significantly after switching to linear control. The advantage of switching to the linear controller is clearly shown by comparing Figure 6 & 3. The swing angle after switching time converges to zero in a short period.

Figure 5 Trolley displacement.

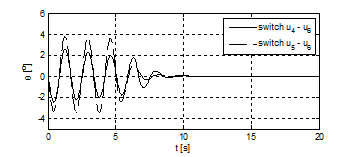
Figure 6 Cable swing angle.

Figure 7 Force on the trolley.

Experiments

The controllers given by Eqs. (25) & (26) combined with Eq. (34) are implemented on the laboratory crane (Figure 8). The trolley is driven by a direct current (DC) motor, and incremental encoders with 1024 counts per revolution are used to measure the trolley displacements and payload swing angle. The crane system is connected to a target personal computer (PC) with two interfaced cards. An NI PCI-6602 card is used to send pulse-width modulation signals to the amplifiers of the DC motor and acquire signals from the encoders. An NI PCI-6025E multifunction card is used to transfer the direction control signals to the motor amplifiers. The target PC is connected to a host PC through RS-232 ports. The overhead crane is controlled by the host PC, which integrates the presented controller designs based on MATLAB/SIMULINK with xPC target solution.

Figure 8 Laboratory overhead crane systems.

The parameters of the laboratory crane are as follows: $m_t=2.0kg$, $m_p=0.85kg$, $l=0.7m$0.7 m, and $g=9.81m/s^2$. The target position of the trolley is set as $x_d=0.5$ m. The parameters of the controllers are chosen as follows:

$k_E=1$, $k_v=2$, $\alpha =1$, $k_p=20,$ $k_d=40$.

The experimental results are presented in Figure 9-11. The trolley reaches the set position after approximately 8s. The swing angle achieves the maximum value of approximately 5° and 10° by the controllers in Eqs. (25) and (26), respectively. The simulation and experimental results show that the controllers derived from$E$achieves better performances than the controllers derived from$E^2$in terms of maximum swing and maximum driving forces. Moreover, system stability is not affected by switching to the LQR controller.

Figure 9 Trolley displacement.

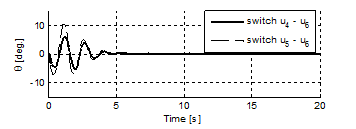
Figure 10 Cable swing angle.

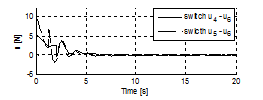
Figure 11 Force on the trolley.

The position control of overhead crane, which is a typical under-actuated system, was compared for five different energy-based control methods. We have designed controllers for under actuated overhead crane systems with an energy-based approach that takes advantage of the passivity of the system. These energy-based nonlinear controllers are most effective for position control of overhead cranes and theoretically ensure asymptotic stability of the system. However, simulations and experimental results show that undesirable cable sway slowly decreases. This tendency is evident when the$E^2$of the total energy is used in controller design. Also, selecting control parameters is another problem of these energy based nonlinear controls. To overcome these problems, the LQR controller is used with conjunction of nonlinear controllers. As the system status approaches the target state, the system switches from the nonlinear controller to the LQR controller. The compared results among the five controllers with switching LQR technique show that the controllers derived from $E$ achieves better performances than the controllers derived from $E^2$ in terms of maximum swing and maximum driving forces. System stability is not affected by switching to the LQR controller.

This research was supported by the Development of Robot System for Inspecting and Cleaning an Industrial Electrostatic Precipitators Program through the MKE (Grant Number: 10067781) and by the Development of Small High-torque MR Brake and High Efficiency Controller funded by Agency for Defense Development of Korea (Grant number: 20170859). It was also supported by the Senior-Friendly Product R&D Program funded by the Ministry of Health and Welfare through the Korea Health Industry Development Institute (HI15C1027).

The author declares there is no conflict of interest.

1. Sun N, Fang Y, Zhang X, Yuan Y. Transportation task-oriented trajectory planning for under actuated overhead cranes using geometric analysis. IET Control Theory & Applications. 2012;6(10):1410–1423.
2. Almutairi NB, Zribi M. Sliding mode control of a three-dimensional overhead crane. Journal of Vibration and Control. 2009;15(11):1679–1730.
3. Chwa, D. Nonlinear tracking control of 3-D overhead cranes against the initial swing angle and the variation of payload weight. IEEE Trans Control Systems Technology. 2009;17(4):876–883.
4. Fang Y, Dixon WE, Dawson DM, et al. Nonlinear coupling control laws for an under actuated overhead crane system. IEEE/ASME Transactions on Mechatronics. 2003;8(3):418–423.
5. Omara HM, Nayfeh AH. Gantry cranes gain scheduling feedback control with friction compensation. Journal of Sound and Vibration. 2005;281(1-2):1–20.
6. Park H, Chwa D, Hong KS. A feedback linearization control of container cranes: varying rope length. Int Journal of Control, Automation, and Systems. 2007;5(4):379–387.
7. Park MS, Chwa D, Hong SK. Antisway tracking control of overhead cranes with system uncertainty and actuator nonlinearity using an adaptive fuzzy sliding-mode control. IEEE Trans Industrial Electronics. 2008;55(11):3972–3984.
8. Tuan LA, Kim GH, Kim MY, et al. Partial feedback linearization control of overhead cranes with varying cable lengths. Int Journal of Precision Engineering and Manufacturing. 2012;13(4):501–507.
9. Zhang X, Gao B, Chen H. Nonlinear controller for a gantry crane based on partial feedback linearization. Int Conference on Control and Automation; 2005:1074–1078.
10. Le Anh Tuan, Tran Ngoc An, Viet-Hung Dang, et al. nonlinear controls of a rotating tower crane in conjunction with trolley motion. Journal of Systems and Control Engineering. 2013;227(5).
11. Le Anh Tuan, VH Dang, ByungSo Kim, et al. Partial feedback linearization control of the three dimensional overhead crane. Int Journal of Control, Automation and Systems. 2013;11(4):718–727.
12. Tuan Anh Le, Soon-Geul Lee. Sliding mode controls of double-pendulum crane systems. Journal of Mechanical Science and Technology. 2013;27(6):1863–1873.
13. Abdel-Rahman EM, Nayfeh AH, et al. Dynamics and control of cranes: a Review. Journal of Vibration and Control. 2003;9: 863–908.
14. Chang C. Adaptive fuzzy controller of the overhead cranes with nonlinear disturbance. IEEE Trans Industrial Informatics. 2007;3(2):164–172.
15. Fang Y, Ma B, Wang P, et al. A motion planning-based adaptive control method for an under actuated crane system. IEEE Trans Control Systems Technology. 2012;20(1):241–248.
16. Hua YJ, Shine YK. Adaptive coupling control for overhead crane systems. Mechatronics. 2007;17(2-3):143–152.
17. Lee HH, Liang Y, Segura D. A sliding mode anti-swing trajectory control for overhead cranes with high speed load hoisting. Journal of Dynamic Systems, Measurements, and Control. 2006;128(4):842–845.
18. Liu D, Yi J, Zhao D, et al. Adaptive sliding mode fuzzy control for a two-dimensional overhead crane. Mechatronics. 2005;15(5):505–522.
19. Tuan Anh Le, Sang-Chan Moon, Won Gu Lee, et al. Adaptive Sliding Mode Control of the Overhead Crane with Varying Cable Length. Journal of Mechanical Science and Technology. 2013;27(3):885–893.
20. Dong Y, Wang Z, Feng Z, et al. Energy based control of a class of underactuated mechanical systems. Congress on Image and Signal Processing. 2008;3:39–143.
21. Fantoni I, Lozano R, Spong MW. Energy based control of the Pendubot. IEEE Transactions on Automatic Control. 2000;45(4):725–729.
22. Li E, Liang ZZ, Hou ZG, et al. Energy-based balance control approach to the ball and beam system. Int Journal of Control. 2009;82(6):981–992.
23. Spong MW, Hutchinson S, Vidyasagar M. Robot dynamics and control. John Wiley & Sons; 2005:1–303.
24. Khalil HK. Nonlinear Systems. 3rd ed. Upper Saddle River, NJ, Prentice Hall; 2002.
25. Ogata K. Modern Control Engineering. Prentice Hall; 2010.