In this paper, a model of elastic rod surrounded by porous media and a model of porous rod surrounded by elastic media are built. Based on the elastic-dynamic theory of liquid-saturated porous solid and numerical computation, the dispersion characteristic of guided waves in this structure with different cylinder radius and porous media parameters are discussed. Results show that the longitudinal guided wave propagation in this structure is dispersive and influenced by the radius of the rod and porosity of the porous media. It suggests that the dispersion curve of L (0,1) shifts to lower frequency with increasing rod radius. The dispersion is mainly influenced by the properties of internal rod. When the internal rod is porous media, the dispersion curves of guided waves gradually shift to low speed with the increasing porosity. The static permeability has little effect on dispersion.All these results can provide a theoretical reference for the non-destructive evaluation to the structure of a solid rod surrounded by infinite media.

Keywords: guided waves, porous media, dispersion

Propagation of guided waves in a solid rod surrounded by infinite media is an interesting research topic of practical importance. One important application is ultrasonic non-destructive evaluation (NDE) of rock bolts. Rock bolts are inserted into the mixture of rock and concrete to ensure the stability of the groundwork. For this research topic, it is important to study the propagation of guided waves in a solid rod surrounded by infinite media. Currently, the topic already has certain research bases.^1–5 However, when anchoring system appears broken rock, or anchor rusty, the elastic media is unable to simulate these situations. Porous media can simulate well. Thus the research of guided wave propagation in a cylindrical structure containing porous media is of great significance. The propagation of guided wave in a multilayer plane porous media has already been widely studied, Parra studied the dispersion and attenuation of acoustic guided waves in layered fluid-filled porous media,⁶ Derible analyzed the transmission coefficient of a water-saturated porous plate⁷ and Fellah studied the time-domain model of transient acoustic wave propagation in layered porous media.^8–10 However, few attentions have been focused on cylindrical waveguide in layered porous media. Most of studies were concentrated in well-logging detection, the structure of which is the internal liquid, external porous media.^11–13 In this paper, for anchoring system, porous media was used to simulate the two cases, one of which is rocks containing cracks and pores; the other is bolt corrosion. Through studying the propagation characteristics of guided wave in the elastic rod embedded in infinite porous media and porous media rod wrapped by infinite elastic media, the results can be a reference for the NDE of rod embedded in infinite media. In this paper, we study the propagation characteristics of guided waves in a solid rod embedded in infinite media with porous media. This paper is arranged as follows. First, the dispersion equations of two models are deduced. Second, the dispersion characteristics of guided waves in the two models are discussed, respectively. Third, we investigated the effects of different porosity parameters and rod radius on the guided waves.

In the description of propagation of elastic waves in porous media, Biot theory is a theoretical model has been widely recognized and applied. According to Biot theory, the porous media is homogeneous and isotropic media constituted by the solid skeleton and pore. The pore distribution is consistent, uniform pore size, communicate with each other. The pores are filled with viscous fluid, the fluid movement relative to the skeleton, the kinematic coupling between each other. The propagation of waves in fluid-saturated porous media meet the stress-strain relationship and the equations of motion, by which the fast P wave, the slow P-wave, S-wave these three kinds of body waves in porous media can be obtained. Fast longitudinal wave is due to the same phase motion between the solid and fluid, slow longitudinal wave is due to the inverting motion between the solid and the fluid.^14,15 The wave number of three body waves are kp1=ωsp1,kp2=ωsp2, kt=ωst. sp1,sp2,st are as following.

$s_{p1,p2}^2=\frac{\gamma }{2}\mp \sqrt{{\left(\frac{\gamma }{2}\right)}^2-\frac{\tilde{\rho }\rho -{\rho }_f{}^2}{HM-C^2}}$                                          (1)

$s_t^2=\frac{1}{N}(\rho -\frac{{\rho }_f{}^2}{\tilde{\rho }})$                                                              (2)

$\gamma =\frac{\rho M+\tilde{\rho }H-2{\rho }_{f}C}{HM-C^2}$                                                      (3)

Where H, M, C and N are four elastic constants of porous media.¹⁶ H, C, M can be expressed as

$M=\frac{K_f{K}_s}{\beta K_s+\left(\alpha -\beta \right)K_f}$                                                        (4)

$C=\alpha M$                                                                          (5)

$H={\alpha }^{2}M+K_b+\frac{4}{3}N$                                                          (6)

$\alpha =1-\frac{K_b}{K_s}$                                                                          (7)

Where K_f is the bulk modulus of the pore fluid, K_s is the bulk modulus of the elastic solid, Kb is the bulk modulus of the porous skeletal frame and N is the shear modulus of the composite as well as that of the skeletal, βis the porosity. ρis the density of the fluid saturated porous media can be got by solid skeleton density ρ_s and fluid density ρ_f.

$\rho =(1-\beta ){\rho }_s+\beta {\rho }_f$                                                            (8)

By introducing the dynamic permeability,¹⁷ the equivalent density $\tilde{\rho }$ associated with inertial force and resistance of the seepage flow can be expressed as

$\tilde{\rho }=\frac{i\eta }{\omega \kappa (\omega )}$                                                                        (9)

$\kappa (\omega )={\kappa }_0{[{(1-\frac{4i{\alpha }_{\infty }^2{\kappa }_0^2{\rho }_f\omega }{{\Lambda }^2{\beta }^2\eta })}^{\frac{1}{2}}-i\frac{\omega {\alpha }_{\infty }{\rho }_f{\kappa }_0}{\beta \eta }]}^{-1}$                  (10)

${\alpha }_{\infty }=\frac{1}{2}({\beta }^{\text{-}1}\text{+}1)$                                                              (11)

Where κ₀is static permeability, η is viscosity coefficient, Λ is pore feature size, α_∞ is porosity curvature. Equation (11) is an approximate formula proposed by Berryman.¹⁸

Elastic rod embedded in infinite porous media

The model1 of this paper is modelled as an infinite long elastic rod embedded in an infinite porous media as shown in Figure 1. It is convenient to solve this problem using cylindrical coordinate, where the z axis of the coordinate is the central axis of the solid rod. In elastic rod, the velocities of longitudinal wave and shear wave, density are denoted by C_l1, C_t1,ρ₁ are respectively. In infinite porous media, the velocities of fast longitudinal wave, slow longitudinal wave and shear wave, solid density and fluid density are denoted by C_fl2,C_sl2,C_t2,ρ_s,ρ_f are respectively. In this paper, only longitudinal modes are taken into consideration. In the frequency-wavenumber domain, the displacement components are given in terms of the potentials $\Phi$  and$\Psi$ . These potentials satisfy the wave equations and respectively denote the compression (P), shear vertical (SV) waves. For elastic rod, the potentials can be expressed as

$\{\begin{array}{c}{\text{Φ}}_1=\left[A_1{I}_0\left({\alpha }_{1}r\right)+K_0\left({\alpha }_{1}r\right)\right]e^{i\left(kz-wt\right)}\\ {\text{Ψ}}_1=A_2{I}_0\left({\beta }_{1}r\right)e^{i\left(kz-wt\right)}\end{array}$             （12）

Where ${\alpha }_1^2=k^2-k_{l1}^2$  ${\beta }_1^2=k^2-k_{t1}^2$ , the wave numbers of the longitudinal and shear body waves of are $k_{l1}\text{=}\omega \text{/}{c}_{l1}$  $k_{t1}\text{=}\omega \text{/}{c}_{t1}$  and the wave number of the guided wave propagating along the z-axis$k\text{=}\omega \text{/v}$  is where x is the angular frequency and v is the unknown phase velocity of guided wave that is dependent on frequency and could be derived by solving the dispersion equation. Further, A₁, A₂ are the unknown coefficients to be determined by the boundary conditions.

Figure 1 The schematic of infinite long elastic rod embedded in infinite porous media.

For infinite porous media wrap layer, the expressions of potential are divided into two parts, solid and liquid phases. For solid phase, the potentials can be expressed as

${\text{Φ}}_{sf}=B_1{K}_0\left({\alpha }_{21}r\right)e^{i\left(kz-wt\right)}$                                          （13）

${\text{Φ}}_{ss}=B_2{K}_0\left({\alpha }_{22}r\right)e^{i\left(kz-wt\right)}$                                       （14）

${\text{Ψ}}_{\text{s}}=B_3{K}_0\left({\beta }_{21}r\right)e^{i\left(kz-wt\right)}$                                                （15）

Thus, the potential of solid compression (P) wave can be expressed as ${\text{Φ}}_s={\text{Φ}}_{sf}+{\text{Φ}}_{ss}$ . Where ${\alpha }_{21}^2=k^2-k_{p1}^2$  ${\alpha }_{22}^2=k^2-k_{p2}^2$  , ${\beta }_{21}^2=k^2-k_t^2$ .The wave numbers of the fast longitudinal wave k_p1 and slow longitudinal wave k_p2 and shear wave k_tcan be obtained by equation (1), (2). B1, B2, B3 are the unknown coefficients to be determined by the boundary conditions.

For liquid phase, the potentials can be expressed as

${\text{Φ}}_f={\eta }_1{\text{Φ}}_{sf}+{\eta }_2{\text{Φ}}_{ss}$                                                           （16）

${\text{Ψ}}_f={\eta }_3{\text{Ψ}}_s$                                                                    （17）

Where η₁, η₂, η₃ are liquid participation factor of two longitudinal shear waves respectively.¹⁹ It is convenient to introduce displacement potentials. And the normal and tangential stress tractions are related to displacements using the Hooke’s law.

The expressions of displacement and stress tractions in elastic media are

$\{\begin{array}{c}{u}_{r1}=\frac{\partial {\text{Φ}}_1}{\partial r}+\frac{{\partial }^2{\text{Ψ}}_1}{\partial r\partial z}\\ u_{z1}=\frac{\partial {\text{Φ}}_1}{\partial z}-\frac{{\partial }^2{\text{Ψ}}_1}{\partial r^2}-\frac{1}{r}\frac{\partial {\text{Ψ}}_1}{\partial r}\end{array}$                                       （18）

$\{\begin{array}{c}{\sigma }_{rr1}=2{\mu }_1\frac{\partial u_r{}_1}{\partial r}+{\lambda }_1\left(\frac{u_r{}_1}{r}+\frac{\partial u_{r1}}{\partial r}+\frac{\partial u_{z1}}{\partial z}\right)\\ {\sigma }_{rz1}={\mu }_1\left(\frac{\partial u_{r1}}{\partial z}+\frac{\partial u_{z1}}{\partial r}\right)\end{array}$             （19）

The expressions of displacement and stress tractions in porous media are

$\{\begin{array}{c}{u}_{rs}=\frac{\partial {\text{Φ}}_s}{\partial r}+\frac{{\partial }^2{\text{Ψ}}_s}{\partial r\partial z}\\ u_{zs}=\frac{\partial {\text{Φ}}_s}{\partial z}-\frac{{\partial }^2{\text{Ψ}}_s}{\partial r^2}-\frac{1}{r}\frac{\partial {\text{Ψ}}_s}{\partial r}\\ u_{rf}=\frac{\partial {\text{Φ}}_f}{\partial r}+\frac{{\partial }^2{\text{Ψ}}_f}{\partial r\partial z}\\ u_{zf}=\frac{\partial {\text{Φ}}_f}{\partial z}-\frac{{\partial }^2{\text{Ψ}}_f}{\partial r^2}-\frac{1}{r}\frac{\partial {\text{Ψ}}_f}{\partial r}\end{array}$                                    （20）

$\{\begin{array}{c}{\sigma }_{rrs}=2N\frac{\partial u_r{}_s}{\partial r}+A\left(\frac{u_r{}_s}{r}+\frac{\partial u_{rs}}{\partial r}+\frac{\partial u_{zs}}{\partial z}\right)+Q\left(\frac{u_{{{}_r}_f}}{r}+\frac{\partial u_{rf}}{\partial r}+\frac{\partial u_{zf}}{\partial z}\right)\\ {\sigma }_{rrf}=Q\left(\frac{u_r{}_s}{r}+\frac{\partial u_{rs}}{\partial r}+\frac{\partial u_{zs}}{\partial z}\right)+R\left(\frac{u_r{}_f}{r}+\frac{\partial u_{rf}}{\partial r}+\frac{\partial u_{zf}}{\partial z}\right)\\ {\sigma }_{rzs}=N(\frac{\partial u_r{}_s}{\partial z}+\frac{\partial u_{zs}}{\partial r})\end{array}$ （21）

Here λ₁,μ₁ are lame constants of the elastic media.A,N correspond to the familiar lame constants of the porous media, A=P-2N.P,Qand R are elastic constants defined by Biot, as shown in equation (22)-(24). The coefficient R is a measure of the pressure required on the fluid to force a certain volume of the fluid into the aggregate while the total volume remains constant. The coefficient Q is of the nature of a coupling between the volume change of the solid and that of the fluid.

$P=\frac{(1-\beta )(1-\beta -K_b/K_s)K_s+\beta K_s{K}_b/K_f}{1-\beta -K_b/K_s+\beta (K_s/K_f)}+\frac{4}{3}N$ （22）

$Q=\frac{(1-\beta -K_b/K_s)\beta K_s}{1-\beta -K_b/K_s+\beta (K_s/K_f)}$                              （23）

$R=\frac{{\beta }^2{K}_s}{1-\beta -K_b/K_s+\beta (K_s/K_f)}$                            （24）

At the interface (r = a), the displacement and stress are continuity. Taking into account the elastic solid impermeable material that restrict the outflow of fluid in porous media on the border, solid skeleton of normal displacement is equal to the fluid normal displacement.¹⁹ The boundary conditions can be written as

$\{\begin{array}{c}{u}_{r1}=(1-\beta )u_{rs}+\beta u_{rf}\\ u_{z1}=u_{zs}\\ {\sigma }_{rr1}={\sigma }_{rrs}+{\sigma }_{rrf}\\ {\sigma }_{rz1}={\sigma }_{rzs}\\ u_{rs}=u_{rf}\end{array}$                                            （25）

By substituting Equations (18),(19),(20),and (21) into Equation (25), the equations can be written as,

$\left[\begin{array}{ccccc}{m}_{11}& m_{12}& m_{13}& m_{14}& m_{15}\\ m_{21}& m_{22}& m_{23}& m_{24}& m_{25}\\ m_{31}& m_{32}& m_{33}& m_{34}& m_{35}\\ m_{41}& m_{42}& m_{43}& m_{44}& m_{45}\\ m_{51}& m_{52}& m_{53}& m_{54}& m_{55}\end{array}\right]\left[\begin{array}{c}{A}_1\\ A_2\\ B_1\\ B_2\\ B_3\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\\ b_4\\ 0\end{array}\right]$              （26）

When the right-hand side of Equation (26) is zero matrixes, the necessary and sufficient condition for the non-zero solutions of the equation is the coefficient determinant$\Delta =0$ . It is the dispersion equation whose solution corresponds to the guided wave. The matrix elements of the 5* 5 matrix for the dispersion equation of guided waves are listed in Appendix A.

Porous rod embedded in infinite elastic media

The model 2 is modelled as an infinite long porous media rod embedded in infinite elastic media as shown in Figure 2. In porous rod, the velocities of fast longitudinal wave, slow longitudinal wave and shear wave, solid density and fluid density are denoted by C_fl,C_sl,C_t,ρ_s,ρ_f are respectively. In infinite elastic media, the velocities of longitudinal wave and shear wave, density are denoted by C_l2, C_t2,ρ₂ are respectively. Similarly, only longitudinal modes are taken into consideration in this model.

Figure 2 The schematic of infinite long porous media rod embedded in infinite elastic media.

For infinite porous media wrap layer, the expressions of potential are divided into two parts, solid and liquid phases. For solid phase, the potentials can be expressed as;

${\text{Φ}}_{sf}=\left[C_1{I}_0\left({\alpha }_{11}r\right)+K_0\left({\alpha }_{11}r\right)\right]e^{i\left(kz-wt\right)}$                   （28）

${\text{Φ}}_{ss}=\left[C_2{I}_0\left({\alpha }_{12}r\right)+K_0\left({\alpha }_{12}r\right)\right]e^{i\left(kz-wt\right)}$                   （29）

${\text{Ψ}}_{\text{s}}=C_3{I}_0\left({\beta }_{11}r\right)e^{i\left(kz-wt\right)}$                                             （30）

Thus, the potential of solid compression (P) wave can be expressed as${\text{Φ}}_s={\text{Φ}}_{sf}+{\text{Φ}}_{ss}$ . Where ${\alpha }_{11}^2=k^2-k_{p1}^2$ ，${\alpha }_{12}^2=k^2-k_{p2}^2$ ，${\beta }_{11}^2=k^2-k_t^2$ .The wavenumbers of the fast longitudinal wave k_p1 and slow longitudinal wave k_p2 and shear wave k_tcan be obtained by equation (1),(2). C1,C2, C3 are the unknown coefficients to be determined by the boundary conditions.

For liquid phase, the potentials can be expressed as

${\text{Φ}}_f={\eta }_1{\text{Φ}}_{sf}+{\eta }_2{\text{Φ}}_{ss}$                                                   （31）

${\text{Ψ}}_f={\eta }_3{\text{Ψ}}_s$                                                                    （32)

Where η₁, η₂, η₃ are liquid participation factor of two longitudinal shear waves respectively.¹⁹ For infinite elastic media, the potentials can be expressed as

$\{\begin{array}{c}{\text{Φ}}_2=D_1{K}_0\left({\alpha }_{2}r\right)e^{i\left(kz-wt\right)}\\ {\text{Ψ}}_2=D_2{K}_0\left({\beta }_{2}r\right)e^{i\left(kz-wt\right)}\end{array}$                                        （33）

Where ${\alpha }_2^2=k^2-k_{l2}^2$  ${\beta }_2^2=k^2-k_{t2}^2$ , the wave numbers of the longitudinal and shear body waves of are $k_{l2}\text{=}\omega \text{/}{c}_{l2}$  $k_{t2}\text{=}\omega \text{/}{c}_{t2}$ .D₁,D₂ are the unknown coefficients to be determined by the boundary conditions. The boundary conditions of this model can be written as;

$\{\begin{array}{c}(1-\beta )u_{rs}+\beta u_{rf}=u_{r2}\\ u_{zs}=u_{z2}\\ {\sigma }_{rrs}+{\sigma }_{rrf}={\sigma }_{rr2}\\ {\sigma }_{rzs}={\sigma }_{rz2}\\ u_{rs}=u_{rf}\end{array}$                                            （34）

When the right-hand side of Equation (34) is zero matrixes, the necessary and sufficient condition for the non-zero solutions of the equation is the coefficient determinant${\beta }_2^2>0$ .It is the dispersion equation whose solution corresponds to the guided wave. By substituting the expressions of displacement and stress tractions, the equations can be written as,

$\left[\begin{array}{ccccc}{m}_{11}& m_{12}& m_{13}& m_{14}& m_{15}\\ m_{21}& m_{22}& m_{23}& m_{24}& m_{25}\\ m_{31}& m_{32}& m_{33}& m_{34}& m_{35}\\ m_{41}& m_{42}& m_{43}& m_{44}& m_{45}\\ m_{51}& m_{52}& m_{53}& m_{54}& m_{55}\end{array}\right]\left[\begin{array}{c}{C}_1\\ C_2\\ C_3\\ D_1\\ D_2\end{array}\right]=\left[\begin{array}{c}{c}_1\\ c_2\\ c_3\\ c_4\\ c_5\end{array}\right]$       （35）

For waveguide mode propagating along a solid rod, the phase velocity must be less than the velocity of shear wave in wrapping media layer,¹ which is${\beta }_{21}^2>0$ , ${\beta }_2^2>0$ . When this condition is satisfied, the guided wave can propagate stalely along the solid rod with non-energy radial diffusion. As the dissipative effect of porous media in model1, 2, the roots of dispersion equation (27), (35) are complex, which means to attenuation. Thus it cannot be called guided wave strictly. However, as the imaginary part of the root is very small, equivalent to small attenuation coefficient, most people still called the case of the guided wave. In this paper, the dispersion equations of different porous media parameters and different internal cylinder radius were solved by numerical methods, and then the dispersion characteristics of guided waves were analyzed.

In this paper, the material properties are listed in Table 1. The material properties²⁰ have been chosen that the two models do not satisfy the existence condition of a Stoneley wave.²¹

The bulk modulus of the porous skeletal frame and the shear modulus of the porous skeletal frame can be obtained by self-consistent formula of composite media equivalent elastic modulus.¹⁹ Under different porosity, bulk modulus of solid skeleton K_b and shear modulus of solid skeleton N will change as shown in Figure 3. When the porosity is 0.5, the porous media²² becomes suspension, shear modulus is near to zero, and the bulk modulus is close to bulk modulus of fluid. For rock materials, the porosity of which is less than 0.2, so we only study the case of porosity less than 0.3. As can be seen, the bulk modulus and shear modulus of the porous skeletal frame decrease as the porosity increasing.

Figure 3 Bulk modulus and shear modulus of the porous skeletal frame with different porosity.

Dispersion properties

In this paper, the dispersion equation was solved with the method of local peak search, depending on the exact roots and tracking curve technology proposed by Lowe^4,23 In order to verify the correctness of the above theory and calculation methods again, the porosity β of porous media was set to zero. The dispersion curves of this case were compared to dispersion curves with the same internal elastic rod material and external elastic material, which was Hanyin Cui’s result.² As shown in Figure 4, the dispersion curves of these cases are fully consistent.

Figure 4 The dispersion comparison between elastic media, model1 and model2 of porosity 0.

Through numerical computing with parameters in Table 1 & Table 2 in which the porosity is 0 and the Static permeability is 10^-12m², the dispersion characteristics of phase velocity and group velocity are analysed. The dispersion curves of the longitudinal modes of model1 and model2 are presented in Figure 5.The model predicts that regardless of mode, both the phase and group velocity dispersion curves tend towards the same high-frequency asymptote as shown in Figure 5.This is the shear velocity of solid rod. For model1, it’s the shear velocity of elastic media (2100m/s). For model2, it’s the shear velocity of porous media (1980m/s). Any mode, whose high-frequency asymptote is shear velocity of the internal rod, is named as a normal mode. In model1 and model2, all the modes are normal modes. For normal modes, each one of the dispersion curves begins at its cutoff frequency where phase velocity is equal to the shear velocity of the wrapping layer that is 2880m/s in model1 and 3100m/s in model 2.The group velocity describe how fast the wave package is travelling through the rock bolt and the time distortion of the received pulse. For model 1, each mode of group velocity dispersion curves increases with the frequency. The group velocity reaches a minimum at the cutoff frequency. For model2, the group velocity with increasing frequency to drop to a minimum, and then increases with frequency and eventually approaches the shear wave velocity of porous media rod. Since the phase velocity is greater than shear velocity of solid rod, β₁, β₁₁ arepure imaginary. For acoustic field of internal rod, the displacement of SV wave in equation (12) and (13) oscillates with the radius, and approaches the maximum in the centre of the rod. As the phase velocity is less than shear velocity of wrapping layer,α₂₁, β₂₁, α₂, β₂ are real number. For acoustic field of wrapping layer, the displacement of fast longitudinal wave and shear wave in equation (13),(15) and (33) decays exponentially with increasing radius.

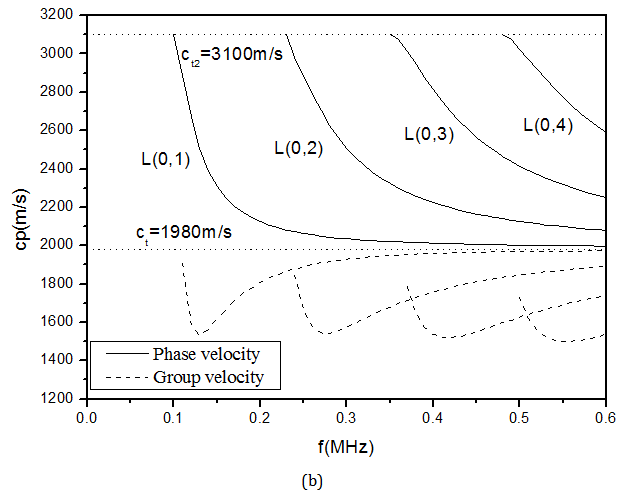
Figure 5 The dispersion curves of the longitudinal modes L (0,p). (a) and (b) present the dispersion curves of model1 and model2, respectively.

Impact of internal rod radius on the dispersion

Considering the model structure is an important factor to guided wave dispersion, the impact of internal rod radius on dispersion was analysed. By setting the parameters as Table 1 & Table 2, the dispersion curves of L (0,1) with different internal rod radius were shown in Figure 6. As can be seen from the Figure 6, either model1 or model2, the dispersion curve of L (0,1) shifts to lower frequency. The cut-off frequency decreases with the increasing radius. The phase velocity at cut-off frequency is still shear velocity of the outside layer without changing with rod radius.

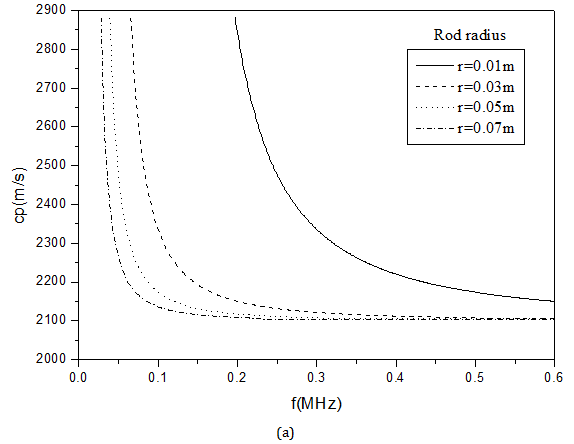
Figure 6 Dispersion curves with different rod radius. (a) and (b) present the dispersion curves of model1 and model2, respectively.

Impact of porous parameters on the dispersion

Considering that the porosity and static permeability are important parameters of porous media, the impact of these two parameters on the dispersion were analysed in this section. In order to determine the effects of the porosity on dispersion, the dispersion characteristics with porosity of 0.1, 0.2, 0.3 were analysed by setting the static permeability κ₀ = 10^-12m².As can be seen from Figure 7, the velocity of bulk wave in porous media changes with porosity for model1. The velocity of bulk wave in porous media of model 2 has the same variation. It also can be found that the frequency do little influence on the velocity of fast longitudinal wave and shear wave, while the velocity of slow longitudinal wave changes with frequency in the range of low frequency. It’s mainly due to the motion of the pore fluid and solid skeleton. The relative motion between the pore fluid and solid skeleton follows the Darcy law. It is influenced by the viscous force and the inertia force. In the range of low frequency, the viscous force of pore fluid plays a predominant role. That leads to velocity dispersion.

Figure 7 Bulk wave velocity of porous media with different porosity of model1.

Since the guided waves propagate along the solid rod, the phase velocity should be less than the velocity of shear wave of the wrapping layer.¹ For model1, the phase velocity of guided wave should be in the range of [c_t1,c_t]. For model2, the phase velocity should be in the range of [c_t,c_t2]. The dispersion curves with different porosity were shown in Figure 8.

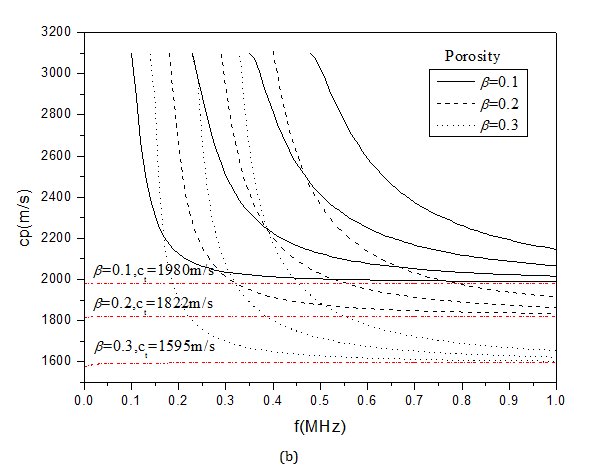
Figure 8 Dispersion curves with different porosity. (a) and (b) present the dispersion curves of model1 and model2, respectively.

Figure 8a Shows the dispersion with different porosity of model1.It can be found that the phase velocity at the cut-off frequency is the shear wave velocity of porous media. That is 2880m/s, 2617m/s, 2263m/s with porosity of 0.1,0.2,0.3 are respectively. The cut-off frequency of the same guided wave mode increases with the increase of porosity. Under the different porosity, the trend of dispersion curves remains unchanged. As shown in Figure 8a, dispersion curves under three kinds of porosity coincide within the corresponding range. The phase velocity of the lowest mode gradually approach to the shear-wave velocity (3260m/s) of the solid elastic rod with increasing frequency.

Figure 8b shows the dispersion with different porosity of model2.As can be seen, the phase velocity at the cut-off frequency remains unchanged when porosity changes. With the increasing porosity, dispersion curves of guided waves gradually shift to low speed. The phase velocity dispersion curve approach to the shear-wave velocity of the internal porous media with increasing frequency. The shear-wave velocity of the internal porous media is 1980m/s, 1822m/s, 1595m/s with porosity of 0.1, 0.2, and 0.3 are respectively. Comparing the dispersion characteristic of model1 and model2, the dispersion is mainly influenced by the properties of internal rod. When the porous media is in wrapping layer (model1), the porosity has little effect on the dispersion. When the porous media is in rod (model2), the dispersion curves make a great change with the changing of porosity. Permeability is an important parameter of porous media, which reflects the ability of porous media transfer fluid. In order to determine the effects of the static permeability on dispersion, the dispersion characteristics with static permeability κ₀ of 10^-11m², 10^-12m², 10^-13m² were analysed by setting the porosity β=0.1.

The dispersion curves with different static permeability were shown in Figure 9. Figures 9a & Figure 9b present the dispersion curves of model1 and model2, respectively. As can be seen from the Figure9, the static permeability has little influence on the dispersion whether for model1 and model 2. By analysing the three bulk wave velocity under different static permeability as shown in Table 3, we found that the static permeability have little effect on the bulk wave velocity. Thus the impact on the dispersion curve is small.

Figure 9 Dispersion curves of longitudinal modes with different static permeability.

In this paper, based on the elastic-dynamic theory of liquid-saturated porous solid, the propagation characteristic of guided waves in a rod surrounded by infinite media with porous media is studied. The dispersion equations of an elastic rod surrounded by porous media and a porous rod surrounded by elastic media have been deduced via wave equation of the guided waves. The impact of the rod radius and porous parameters on dispersion are discussed. The results show that the longitudinal guided wave propagation in the two models of this paper is dispersive and the dispersion curves tend towards the same high-frequency asymptote which is shear velocity of solid rod. The dispersion curve of L (0,1) shifts to lower frequency with increasing rod radius.By comparing the dispersion characteristic of model1 and model2, the dispersion is mainly influenced by the properties of internal rod. When the internal rod is porous media, the dispersion curves of guided waves gradually shift to low speed with the increasing porosity. The static permeability has little effect on dispersion.

This work was supported by the Natural Science foundation of China Grant No 11574072 and 11274091, Key research project of Jiangsu Grant No BE2016056.

Author declares there is no conflict interest.

1. Hanyin Cui, Bixing Zhang. Guided Waves in Cylindrical Multi-layered Media. IEEE International Ultrasonics Symposium Proceedings. 2008. p. 912–915.
2. Cui HY, Zhang BX, Johnstone S, et al. Excitation and mechanisms and dispersion characteristics of guided waves in multilayered cylindrical solid media. The Journal of the Acoustical Society of America. 2012;131(3):2048–2062.
3. MD Beard, MJS Lowe, P Cawley. Development of a guided wave inspection technique for rock bolts. AIP Conference Proceedings. 2012;615:1318–1325.
4. MD Beard, MJS Lowe. Non-destructive testing of rock bolts using guided ultrasonic waves. International Journal of Rock Mechanics and Mining Sciences. 2003;40(4):527–536.
5. MD Beard, MJS Lowe, P Cawley. Inspection of rock bolts using guided ultrasonic waves. AIP Conference Proceedings. 2001;557(1):1156–1163.
6. Jorge O Parra, Pei-cheng Xu. Dispersion and attenuation of acoustic guided waves in layered fluid-filled porous media. The Journal of the Acoustical Society of America. 1994;95(1):91–98.
7. Serge Derible. Debye-series analysis of the transmission coefficient of a water-saturated porous plate obeying Biot’s theory. The Journal of the Acoustical Society of America. 2005;118(6):3430–3435.
8. ZEA Fellah, A Wirgin, M Fellah, et al. A time-domain model of transient acoustic wave propagation in double-layered porous media. The Journal of the Acoustical Society of America. 2005;118(2):661–667.
9. ZEA Fellah, S Berger, W Lauriks, et al. Measuring the porosity and tortuosity of porous materials via reflected waves at oblique incidence. The Journal of the Acoustical Society of America. 2003;113(5):2424–2433.
10. ZEA Fellah, M Fellah, W Lauriks, et al. Solution in time domain of ultrasonic propagation equation in a porous material. Wave Motion. 2003;38:151–163.
11. Guan W, Hu HS, He X. Finite-difference modeling of the monopole acoustic logs in a horizontally stratified porous formation. The Journal of the Acoustical Society of America. 2009;125(4):1942–1950.
12. LI Wei, HU Hengshan, Zhang Bixing, et al. Simulation of acoustic well-logging wave field in a radially multilayered fluid-saturated porous formation. Acta Acustica. 2010;35(4):456–464.
13. Wang X, Dodds K. Effects of the outermost boundary on acoustic waves in an artificial cased borehole. Exploration Geophysics. 2012;33:146–152.
14. MA Biot. Theory of propagation of elastic waves in a fluid saturated porous rock I. Low frequency range. The Journal of the Acoustical Society of America. 1956;28(2):179–191.
15. M Stern, A Bedford, HR Millwater. Wave Reflection from a Sediment Layer with depth-dependent properties. The Journal of the Acoustical Society of America. 1985;77(5):1781–1788.
16. MA Biot. Mechanics of Deformation and Acoustic Propagation in Porous Media. Journal of Applied Physics. 1962;33(4):1482–1498.
17. DL Johnson, J Koplik, R Dashen. Theory of Dynamic Permeability and Tortuosity in Fluid-saturated Porous Media. Journal of Fluid Mechanics. 1987;176:379–402.
18. James G Berryman. Long-wavelength propagation in composite elastic media II.Ellipsoidal inclusions. The Journal of the Acoustical Society of America. 1980;68(6):1820–1831.
19. ZHAO Chenggang, GAO Fuping. Boundary effect of propagating from liquid-filled porous media to solid media. Earthquake Engineering and Engineering Vibration. 1999;19(1):1–6.
20. GWC Kaye, TH Laby. Acoustics in Tables of Physical and Chemical Constants. Chapter 2, Longman, England.
21. JL Rose. Interface waves in Ultrasonic Waves in Solid Media. Chapter 9, Cambridge University Press, USA. 2004.
22. Shvidler MI. Determination of self-consistent effective parameters in transport problems in porous media. Fluid Dynamics. 1981;16(3):374–380.
23. MA Qi, HU Wenxiang. Methods for Analyzing and Solving Dispersion Characteristics of Leaky Modes of Layered Structures Immersed in Fluid. Technical Acoustics. 2013;32(4):513–516.