According to classical physics theories, a moving particle cannot move to an environment with greater potential energy than its total energy during movement. But according to quantum theories, this event is well known. This event is called tunneling. Tunneling is a probability, and it is measured by a transmission coefficient. Correct calculation of this coefficient is very important because very sensitive and important instruments have been developed based on this event, and many events in nature can be explained by tunneling. This coefficient is generally calculated by semi-classical approaches (WKB) and the known formula is an approximate formula. In previous publications, the general transmission coefficient of a potential barrier with arbitrary form is calculated by a simple method without any approximation. The results are applied to calculate the half-life values of the nuclei that emit alpha particles. The half-life values obtained from our calculations and the classical method (WKB) have been compared, and it has been found that the new half-life values are exactly consistent with the experimental values. In this article, this general transmission coefficient is applied to calculate transmission coefficient for an arbitrary form external electrical field barrier (cold emission by the metal). The values obtained from our calculations and those of classical method (WKB) have been compared.

Keywords: tunneling, transmission coefficient, cold emission by metal, barrier of electrical field

When a flowing particle or particle current is encountered with a potential energy barrier greater than its total energy, it cannot pass the potential barrier and returns to its environment or disappears within the potential according to classical physics. However, the observations indicate that such a particle or particle current may pass through the potential barrier. In quantum physics, this phenomenon is called tunneling. This phenomenon cannot be explained according to classical physics theories. One of the greatest achievements of quantum physics theory is that it can explain the tunneling or tunneling event. The probability of passing of the particles through the potential barrier is determined by the passing or transmission coefficient. This coefficient indicates the possibility of passing the potential barrier of the particle. Where and how this coefficient is used can be found in many publications. It is also a fact that some very sensitive instruments are based on the phenomenon of this formula. This well-known formula is obtained by a semi-classical calculation method called Wentzel-Kramers-Brillouin (WKB) Method in Quantum Mechanics and is an approximate formula as its name suggests. In previous articles,^1–3 a new general formula is obtained without any approximation and this formula can be easily applied to any form of potential barrier. This formula is shown to be more accurate and realistic, applying to the alpha decay of some well-known atomic nuclei in nuclear physics.²

The field emitted current density is computed with the barrier transmission coefficient. The analytical method generally used is WKB which is not reliable especially at high fields (the barrier is not slowly varying).Many researchers and engineers are researching these topics, on the physics electron emission of electrons from metal under high electric and high temperature. They make use of tunneling in their researches such as tunnel diode, Josephson joint, scanning tunneling microscope, etc. It is possible for these researchers to get correct results in their studies by calculating the tunneling coefficient precisely.It can be thought that the results found with this study will be very useful for the researchers who make scientific and technological studies in the above mentioned subjects. With our formula of the transmission coefficient they will be able toimprove the analytical equation. For this purpose, this article was prepared. In this article, the general transmission coefficient is applied to calculate cold emission (radiation of an atom in the electric field) by the metals. The values obtained from our calculations and those of classical method (WKB) have been compared.

The new transmission coefficient (or the barrier penetration probability)is given as follows:

${\text{T}}_{\text{new}}=\frac{2}{\cosh \left[2\text{ K d}\right]+\text{cos}\left[2\text{ P}\right]}$     (1)

$m_1=\sqrt{\frac{2m}{{\hslash }^2}};K=m_1\sqrt{E};Q\left(r\right)=m_1{{\displaystyle \int }}^{\text{}}\sqrt{U\left(r\right)}dr;P=Q\left(r_2\right)-Q\left(r_1\right)=\sqrt{\frac{2m}{{\hslash }^2}}\underset{r_1}{\overset{r_2}{{\displaystyle \int }}}\sqrt{U\left(r\right)}dr$

Here, U(r) is potential function of barrier; mass or reduced mass of particle that hits and leaves the potential barrier, respectively. are abscises of the points that the particle hits and leaves the potential barrier, respectively and they are found solving the equation E=U(r); $d=r_2-r_1,\left(r_1<r_2\right),d$ is the barrier width. E is the total energy of the particle passing through the obstacle.^1–3 From the literature,^4–8 the WKB transmission coefficient (or the barrier penetration probability) which is calculated by the method WKB is known as follows:

$T_{WKB}=e^{-2g},[g=\sqrt{\frac{2m}{{\hslash }^2}}\underset{r_1}{\overset{r_2}{{\displaystyle \int }}}\sqrt{U\left(r\right)-E}dr=m_1\underset{r_1}{\overset{r_2}{{\displaystyle \int }}}\sqrt{U\left(r\right)-E}dr]$     (2)

The energy gained by the atom in the electric field

When an atom is placed in a constant external electric field, the energy levels change. This phenomenon is called the Stark effect. The electric field interacts with the electrical dipole moment of atom. Considering a uniform electric field $\vec{\epsilon }$  along the z-axis, the energy gained from the interaction with the electric field is as follows:

$E_e=\vec{D}.\vec{\epsilon }=\epsilon D\cos \cos \left(\theta \right)$       (3)

Here D is electrical dipole moment of atom; θ is the angle between the vectors of $\vec{\epsilon }and\vec{D}.$   The electric field can be strong or weak. If the electric field is taken in the direction of $z-axis$ , then $\theta =0$ becomes and Equation (3) takes the following form:

$E_e=U(r)=\vec{D}.\vec{\epsilon }=\epsilon D=-e\epsilon r$       (4)

Here e is the electrical charge of electron, is the radially variable in spherical coordinates.

Calculation of transmission coefficient

Emission of electrons from a metal surface is the basis of an important device known as scanning tunneling microscope (STM). An STM consists of a very sharp conducting probe which is scans over the surface of a metal (or any other solid conducting medium). A large voltage difference is applied between the probe and the surface. The surface electric field strength immediately below the probe tip is proportional to the applied potential difference, and inversely proportional to the spacing between the tip and the surface. Electrons tunneling between the surface and the probe tip cause a weak electric current. The magnitude of this current is proportional to the tunneling probability  It follows that the current is an extremely sensitive function of the surface electric field strength, and, hence, of the spacing between the tip and the surface (assuming that the potential difference is held constant). An STM can thus be used to construct a very accurate contour map of the surface under investigation. In fact, STMs are capable of achieving sufficient resolution to image individual atoms.

Suppose that a metal surface is subject to a large uniform external electric field of strength $\epsilon$ , which is directed such that it accelerates electrons away from the surface. The electrons just below the surfaceof a metal can be regarded as being in a potential well of depth W, where W is called the work function of the surface. Adopting a simple one dimensional treatment of the problem let the metal lie at r<0, and the surface at r=0. The applied electric field is shielded from the interior of the metal. Hence, the energy E, for example, of an electron just below the surface is unaffected by the field. In the absence of the electric field, the potential barrier just above the surface is simply $U\left(r\right)-E=W$ . The electric field modifies this to $U\left(r\right)-E=W-e\epsilon r$ . The potential barrier is sketched in Figure 1. It can be seen in Figure 1 that an electron just below the surface of the metal is confined by a triangular potential barrier which extends from $r=r_{1}to{r}_2$ , where $r_1=0and{r}_2=\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$(e\epsilon )$}\right..$  In Equation (1), if the following values are taken,

$d=r_2-r_1=\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$\left(e\epsilon \right)$}\right.;m_1=\sqrt{\frac{2m}{{\hslash }^2}}=\raisebox{1ex}{$\sqrt{2m}$}\!\left/ \!\raisebox{-1ex}{$\hslash $}\right.$  ;  $K=\sqrt{\frac{2m}{{\hslash }^2}E}=m_1\sqrt{-\left|E\right|}=i{m}_1\sqrt{W}$   ; $W=\left|E\right|$  

$Q\left(r\right)=m_1{{\displaystyle \int }}^{\text{}}\sqrt{-e\epsilon r}dr=i\frac{2\sqrt{2me\epsilon }}{3\hslash }{r}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=i\sqrt{\frac{8me\epsilon }{9{\hslash }^2}}{r}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ ;  $P=Q\left(r_2\right)-Q\left(r_1\right)=i\frac{\sqrt{8m{W}^3}}{3e\epsilon \hslash }$

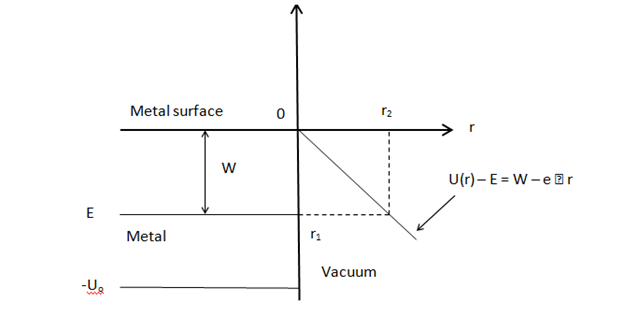
Figure 1 The potential barrier versus position for an electron in a metal. The potential energy is -U₀ when the electron is in the metal (r<0) and is proportional to r outside the metal (r>0). An electron with energy E can escape the metal by tunneling from r₁=0 to the point r₂

The following transmission coefficient formula is obtained:

$T_{new}=\frac{2}{\cosh \cosh \left[2Kd\right]+\cos \cos \left[2P\right]}=\frac{2}{\cos \left[\frac{2\sqrt{2m}}{\hslash e\epsilon }{W}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right]+\cosh \left[\frac{4\sqrt{2m}}{3\hslash e\epsilon }{W}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right]}$      (5)

Using the WKB approximation, the probability of such an electron tunneling through the barrier and consequently the probability of this electron being emitted from the surface is calculated as follows:

$T_{WKB}=\exp \left[-2m_1\underset{r_1}{\overset{r_2}{{\displaystyle \int }}}\sqrt{U\left(r\right)-E}\right]dr=\exp \left[-2m_1\underset{r_1}{\overset{r_2}{{\displaystyle \int }}}\sqrt{W-e\epsilon r}\right]dr$

$T_{WKB}=\exp \left[-\frac{4\sqrt{2m}}{3\hslash e\epsilon }{W}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right]$      (6)

The above result given in Equation (6) is known as the Fowler-Northeim formula. This formula is the result of WKB approximation. The formula given in Equation (5) is exact formula because there is no approximation. It is seen that there are a lot of difference between them. If the ratio of T_new T_WKB to iscalculated, the following value is obtained:

$\raisebox{1ex}{$T_{new}$}\!\left/ \!\raisebox{-1ex}{$T_{WKB}$}\right.\approx 4$      or $T_{new}\approx 4T_{WKB}$     (7)

Both values appear to be very different. It is necessary to accept that T_new  is more accurate because no approximation was made while calculating this formula.

Numerical calculations and comparison of equations (5) and (6)

The barrier penetration probabilities or the transmission coefficients  have been calculated from Equations (5) and (6). In the calculations, the electron mass, $m{c}^2=0.511003MeV;$  the electron charge, $e=1.19999{\left(MeV.fm\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$  have been taken. The obtained values for the different metals are seen in Table 1. In Table 1, it can be seen that the new method is more appropriate than the classical WKB method. In the calculations of the current-voltage characteristics of a diode in semiconductor physics, it is expected to have better results. In calculations, one has been taken $\hslash c=197.329MeV.fm$ . Numerical calculations were made for three different electric fields, and the results are shown in Table 1. The values of work function (W).⁹ Calculations were done for three values of electric field. $[\epsilon \left(\raisebox{1ex}{$V$}\!\left/ \!\raisebox{-1ex}{$cm$}\right.\right)=5\times {10}^6,5\times {10}^7,1\times {10}^7]$ .

In previous articles,^1–3 the general transmission coefficient formula for a potential barrier with an arbitrary form has been easily calculated without making any approximation. In the above calculation, the new method that we developed for the solution of the radial SE has been used. The general transmission coefficient obtained from the new method is given by the formula (1). In this formula, it could be difficult to calculate analytically the integral ${{\displaystyle \int }}^{\text{}}\sqrt{U(r)}dr$ . If these calculations cannot be made analytically, they should then be performed by numerical calculation methods.

Hence, it is said that the results obtained using the new formula are more realistic. In the  method, the wave function is sinusoidal before and after the potential barrier. However, it is not a sinusoidal but an exponential function in the potential barrier. So, the wave function inside the potential barrier is not sinusoidal; after the potential barrier, it becomes sinusoidal again. However in the new method, the wave functions are sinusoidal everywhere both inside and outsides of the potential barrier. But, the wave functions have different phases inside and outside the potential barrier and it advances everywhere as sinusoidal functions. This is more reasonable. It can also be said that it is more accurate and realistic. Besides, the WKB method gives an approximate wave function. In the new method, the wave function is exact because there is no approximation. That is why the theoretical calculated half-life values match better with the experimental values. From these, we conclude that the transmission coefficient given in Equation (1) is more correct and realistic.

The new general transmission coefficient formula can be used to calculate the other tunneling phenomenon. Here in this short article, we have calculated the transmission coefficient for cold emission from the metals, and results were compared with the results obtained with those of the WKB method. We see that two results were not the same. I have to say that the newly discovered results are more realistic. Therefore, it is expected that this new coefficient will produce very realistic results.

I would like to express my sincere gratitude to my wife Özel and my daughters Işıl and Beril for their help in editing.

Author declare that there is no conflicts of interest.

None.

1. Calculation a New Transmission Coefficient of Tunneling for an Arbitrary Potential Barrier and Application to Alpha Decay of Photonic Materials and Technology. Journal of Photonic Materials and Technology. 2019;5(2):24–31.
2. Ebrahim Shaikh, Md Sanaullah Murad, Taposh Ranjan Sarker, et al. Standard Procedure and Time Setting for Servicing of Single Jersey and Double Jersey Knitting Machie. GJOSFR. 2019;19(1).
3. Erbil HH. General solution of the Schrödinger equation with potential field quantization. Turkish Journal of Physics. 2018;42:527–572.
4. F Schwabl. Quantum Mechanics. 2nd edn. USA: Springer-Verlag, Berlin Heidelberg New York; 1995.
5. L Powell, B Crasemann. Quantum Mechanics. USA: Addison-Wesley Publishing Company Inc; 1965.
6. LD Landau. EM Lifstits. Quantum Mechanics. USA: Pergamon Press; 1958.
7. J Griffiths. Introductory Quantum Mechanics. USA: Prentice Hall; 1994.
8. HH Erbil. Analytics and Quantum Mechanics. Turkey: Nobel Academic Publishing; 2014.
9. RA Serway. Physics For Scientists and Engineers with Modern Physics. 3rd edn. USA: Saunders College Publishing; 1992.