The tremendous strength and light weight properties of Carbon nanotubes (CNTs) have fascinated the interest of researchers and scientists towards using CNTs for thermal, chemical, optical, electrical, structural and mechanical applications. This paper presents analytical solutions to the nonlinear dynamic response, shear force and bending moment of such CNTs. The CNT is modeled via thermal elasticity mechanics and Euler-Bernoulli theories. Without linearization, series expansion or omission of any independent variable, the developed nonlinear model that governs the physics of the behaviour of the CNT when excited by the aforementioned external agents is solved using transient differential transform method (TDTM) and verified with an inbuilt numerical scheme in MAPLE16. The results of the generated close form solution in this work are also compared with those of past works and excellent agreements are achieved. The parametric studies revealed that an increase in pressure term increases CNT deflection for any mode while a corresponding increase in the temperature and foundation parameters have an attenuating impact on deflection. Finally, the dynamic study reveals that locations with maximum bending moments are observed to possess minimum shear forces. It is envisaged that this work will enhance the use of CNTs for structural, electrical and mechanical applications.

Keywords: carbon nanotube, external pressure, dynamic study, transient differential transform method, integral transform

Due to the discovery of the discovery of CNT by Iijima, many researches on carbon nanotubes arrangements have been examined.^1–4 Dynamic investigations have been performed on beams, nano-wires, nano-rods and nano-beam so as to specifically harness the tremendous properties of CNTs for applications such as nanomaterial reinforcement designs. To actualize this, the well know beam models were employed and dynamic ranges were obtained in the stability domain of the vibrating structures.^5–22 Vibration and instability responses of DWCNT have been considered using a nonlinear model with electrostatic actuation as external forcing function.^22–26 They employed an alternating voltage as the exciting agent for vibration and determine the bifurcation limit of the nanotube. It was concluded that both walls operate at the same vibration frequency under the considered resonant conditions. The application of nonlocal theory of elasticity to natural frequency determination had been presented for the first three modes using a simply supported CNT.²⁶ They also illustrated how the frequency in the order of Tera-hertz can be harnessed to find useful applications in optics. Lei et al.²⁷ considered the application of Timoshenko beam theory to the dynamic response of DWCNT. The nonlinear equations derived by Asgharifard Sharabiani & Haeri Yazdi²⁸ found applications in graded nanobeams with moderate surface roughness. Wang²⁹ obtained models for handling the above-mentioned surface roughness effect. He considered a free flow induced vibration in structures based on nonlocal theory of elasticity and discovered the impact of small thickness tube on vibration and stability. In an attempt to model the foundations of CNTs very close to reality, many studies on foundations have been examined after considering CNTs as structures resting on or embedded in elastic foundations such as Pasternak, Winkler, and Visco-Pasternak medium.^30–35 Yinusa & Sobamowo³⁷ performed thermal instability and dynamic response analysis on a tensioned CNT under mobile external pressure. In order to understand the dynamics of branched CNT when induced by fluid flow, Yinusa et al.,³⁸ analyzed a branched CNT with different downstream angles. They formulated a nonlinear vibration model of an embedded branched nanofluid-conveying CNT and obtained the equation of motion using Hamilton principle. They focused on the influences of vital parameters which includes downstream angle, temperature change and two dimensional external magnetic field. They concluded that increase in downstream angles decreases stability while the magnetic term possessed an attenuating impact on system’s response. In order to justify the widespread application of CNTs, different researches in line with experiment, numerical and analytical methods have also been presented.^39–42 The novelty in this present study is the consideration of a nonlinear dynamic scenario which is closer to reality as against the idealized linear vibration model previously considered by Yinusa et al.³⁸ Motivated by these considerations, this work aim to dynamically determine the nonlinear response, shear force and bending moment of a pressurized CNT. Without linearization, series expansion or omission of any independent variable, the developed nonlinear model is solved using transient differential transform method (TDTM). The effects of the External Uniform Pressure, modal number as well as other parameters are presented graphically.

Consider a homogeneous and constant cross-section SWCNT with external exciting pressure as illustrated in Figure 1.

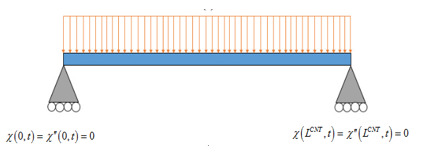
Figure 1 Schematic of the pressurized CNT.

By employing the classic Euler-Bernoulli beam model, the nonlinear vibration of figure 1 can be modelled as;

$E{I}^{CNT}\frac{{\partial }^4\chi }{\partial x^4}+\left(\frac{EA}{1-2v^{\ast }}{\alpha }^{\ast }\theta -T\right)\frac{{\partial }^2\chi }{\partial x^2}+M\frac{{\partial }^2\chi }{\partial t^2}+K\chi +K_p{\chi }^3=P\left(x\right)$     (1)

Substituting for the pressure term,

$E{I}^{CNT}\frac{{\partial }^4\chi }{\partial x^4}+\left(\frac{EA}{1-2v^{\ast }}{\alpha }^{\ast }\theta -T\right)\frac{{\partial }^2\chi }{\partial x^2}+M\frac{{\partial }^2\chi }{\partial t^2}+K\chi +K_p{\chi }^3=\mu A^{CNT}\frac{d}{dx}\left(P_0\left(1+\frac{\delta }{L^{CNT}}x\right)\right)$     .(2)

Method of solution via TDTM

Since the resulting model in equation (4) contains a nonlinear foundation term, the model generally becomes nonlinear and difficult to solve using Laplace and Fourier methods. As a result, TDTM is employed. This method predicts excellently when engaged to handle nonlinear models. In this present study, the nonlinear transient model in Eq. (2) will be solved analytically using the TDTM and verify after removing the nonlinear term with Integral transform method.

Basic principle of the TDTM

TDMT is an extension of the Classical DTM but the former differs from the later due to the inclusion of transient term transformation together with the spatial term. Some basic TDTM recursive relations are shown below Table 1: 

Method of solution: Transient differential transform method (TDTM)

Recall that the nonlinear transient governing equation as shown in Eq. (2) may be expressed as,

$E{I}^{CNT}\frac{{\partial }^4\chi }{\partial x^4}+\left(\frac{EA}{1-2v^{\ast }}{\alpha }^{\ast }\theta -T\right)\frac{{\partial }^2\chi }{\partial x^2}+M\frac{{\partial }^2\chi }{\partial t^2}+K\chi +K_p{\chi }^3=\mu A^{CNT}\frac{d}{dx}\left(P_0\left(1+\frac{\delta }{L^{CNT}}x\right)\right)$     (3)

Subject to the pinned-pinned conditions:

$\begin{array}{l}\chi \left(x,0\right)=\dot{\chi }\left(x,0\right)=0\\ \chi \left(0,t\right)={\chi }^{″}\left(0,t\right)=0\\ \chi \left(L^{CNT},t\right)={\chi }^{″}\left(L^{CNT},t\right)=0\end{array}$

Applying the TDTM illustrated in table 1, the recursive relation of Eq. (3) becomes;

$\begin{array}{l}E{I}^{CNT}\left(k+1\right)\left(k+2\right)\left(k+3\right)\left(k+4\right)\chi \left[k+4,h\right]+\left(\frac{EA}{1-2v^{\ast }}{\alpha }^{\ast }\theta -T\right)\left(k+1\right)\left(k+2\right)\chi \left[k+2,h\right]\\ +M\left(h+1\right)\left(h+2\right)\chi \left[k,h+2\right]+K\chi \left[k,h\right]\\ +K_p{\displaystyle \sum _{r=0}^k{\displaystyle \sum _{s=0}^{k-r}{\displaystyle \sum _{u=0}^h{\displaystyle \sum _{v=0}^{h-u}\chi \left[r,h-u-v\right]\chi \left[s,u\right]\chi \left[k-r-s,v\right]}}}}\\ =\mu A^{CNT}{P}_0\frac{\delta }{L^{CNT}}\sigma \left[k,h\right]\end{array}$     (4)

Where the recursive term  

$\sigma \left[k,h\right]=\{\begin{array}{l}1ifk=h=0,\\ \\ \\ 0otherwise\end{array}$     (5)

On re-arranging Eq. (4), we have the finalized TDTM recursive equation as

$\chi \left[k+4,h\right]=\frac{1}{E{I}^{CNT}\left(k+1\right)\left(k+2\right)\left(k+3\right)\left(k+4\right)}\left(\begin{array}{l}-\left(\frac{EA}{1-2v^{\ast }}{\alpha }^{\ast }\theta -T\right)\left(k+1\right)\left(k+2\right)\chi \left[k+2,h\right]\\ -M\left(h+1\right)\left(h+2\right)\chi \left[k,h+2\right]+K\chi \left[k,h\right]\\ -K_p{\displaystyle \sum _{r=0}^k{\displaystyle \sum _{s=0}^{k-r}{\displaystyle \sum _{u=0}^h{\displaystyle \sum _{v=0}^{h-u}\chi \left[r,h-u-v\right]\chi \left[s,u\right]\chi \left[k-r-s,v\right]}}}}\\ +\mu A^{CNT}{P}_0\frac{\delta }{L^{CNT}}\sigma \left[k,h\right]\end{array}\right)$     (6)

Subject to the TDTM transformed conditions:

$\begin{array}{l}\chi \left(k,0\right)=\chi \left(k,1\right)=0\\ \chi \left(0,h\right)=\chi \left(2,h\right)=0\\ \chi \left(1,h\right)=a,\chi \left(3,h\right)=b\end{array}$     (7)

Where the constants will be determined by the remaining two boundary conditions. Solving Eq. (6) with Eq. (7), the term by term TDTM solutions are obtained as shown below:

${\chi }_{4,0}=1/24\frac{\mu A{P}_o\delta }{E{I}^{CNT}{L}^{CNT}}$

${\chi }_{4,1}=0,{\chi }_{4,2}=0,{\chi }_{4,3}=0,{\chi }_{4,4}=0$

${\chi }_{4,5}=-7/4\frac{M{\chi }_{0,7}}{E{I}^{CNT}}$

${\chi }_{5,0}=-\frac{Ma}{60E{I}^{CNT}}$

${\chi }_{5,1}=-1/20\frac{Ma}{E{I}^{CNT}}$

${\chi }_{5,2}=-\frac{1}{120E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+12Ma+Ka\right)$

${\chi }_{5,3}=-\frac{1}{120E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+20Ma+Ka\right)$

${\chi }_{5,4}=-\frac{1}{120E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+30Ma+Ka\right)$

${\chi }_{5,5}=-\frac{1}{120E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+42M{\chi }_{1,7}+Ka\right)$

${\chi }_{6,0}=-\frac{\mu A{P}_o\delta }{720{\left(E{I}^{CNT}\right)}^2{L}^{CNT}}\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)$

${\chi }_{6,1}=0,{\chi }_{6,2}=0,{\chi }_{6,3}=0,{\chi }_{6,4}=0$

${\chi }_{6,5}=-\frac{1}{360E{I}^{CNT}}\left(-21\frac{M{\chi }_{0,7}}{E{I}^{CNT}}\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)+42M{\chi }_{2,7}\right)$

TDTM series solution is generally represented as;

$\chi \left(x,t\right)={\displaystyle \sum _{j=0}^{\infty }{\displaystyle \sum _{l=0}^{\infty }{\chi }_{j,l}{x}^j{t}^l}}$     (8)

The TDTM series solution then becomes;

Equation (9) is the desired TDTM solution that represents deflection of the SWCNT. 

Determination of the SWCNT Bending moment and Shear force from TDTM

The Bending moment is related to the SWCNT deflection by

${\rm B}\left(x,t\right)=-E{I}^{CNT}\frac{{\partial }^2\chi }{\partial x^2}$     (10)

Similarly, the Shear force is related to the SWCNT deflection by

$S\left(x,t\right)=-E{I}^{CNT}\frac{{\partial }^3\chi }{\partial x^3}$     (11)

Substituting Eq. (9) into Eqs. (10-11), we have for the nonlinear bending moment,

$B\left(x,t\right)=\left\{\begin{array}{l}6bx{t}^5+6bx{t}^4+6bx{t}^3+6bx{t}^2\\ +1/2\frac{\mu A{P}_o\delta x^2}{E{I}^{CNT}{L}^{CNT}}-21\frac{M{\chi }_{0,7}{x}^2{t}^5}{E{I}^{CNT}}\\ -1/3\frac{Ma{x}^3}{E{I}^{CNT}}-\frac{Ma{x}^{3}t}{E{I}^{CNT}}-1/6\frac{x^3{t}^2}{E{I}^{CNT}}\left(\begin{array}{l}6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b\\ +12Ma+Ka\end{array}\right)-\\ 1/6\frac{x^3{t}^3}{E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+20Ma+Ka\right)\\ -1/6\frac{x^3{t}^4}{E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+30Ma+Ka\right)-\\ 1/6\frac{x^3{t}^5}{E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+42M{\chi }_{1,7}+Ka\right)\\ -1/24\frac{\mu A{P}_o\delta x^4}{{\left(E{I}^{CNT}\right)}^2{L}^{CNT}}\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)\\ -1/12\frac{x^4{t}^5}{E{I}^{CNT}}\left(-21\frac{M{\chi }_{0,7}}{E{I}^{CNT}}\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)+42M{\chi }_{2,7}\right)\end{array}\right\}$     (12)

With a shear force expressed as,

$S\left(x,t\right)=\left\{\begin{array}{l}6b{t}^5+6b{t}^4+6b{t}^3+6b{t}^2+\frac{\mu A{P}_o\delta x}{E{I}^{CNT}{L}^{CNT}}\\ -42\frac{M{\chi }_{0,7}x{t}^5}{E{I}^{CNT}}-\frac{Ma{x}^2}{E{I}^{CNT}}-3\frac{Ma{x}^{2}t}{E{I}^{CNT}}-\\ 1/2\frac{x^2{t}^2}{E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+12Ma+Ka\right)\\ -1/2\frac{x^2{t}^3}{E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+20Ma+Ka\right)\\ -1/2\frac{x^2{t}^4}{E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+30Ma+Ka\right)-\\ 1/2\frac{x^2{t}^5}{E{I}^{CNT}}\left(6\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)b+42M{\chi }_{1,7}+Ka\right)\\ -1/6\frac{\mu A{P}_o\delta x^3}{{\left(E{I}^{CNT}\right)}^2{L}^{CNT}}\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)\\ -1/3\frac{x^3{t}^5}{E{I}^{CNT}}\left(-21\frac{M{\chi }_{0,7}}{E{I}^{CNT}}\left(\frac{E{A}^{CNT}\overline{\alpha }\theta }{1-2\overline{v}}-T\right)+42M{\chi }_{2,7}\right)\end{array}\right\}$     (13)

Verification

The present study is verified with numerical method and a good agreement is reached as shown (Table 2): 

Influence of Pressure, temperature and foundation parameters on CNT deflection

Figures 4–7 depict the influence of external pressure, temperature and foundation parameter on the steady state response of the CNT. Increasing external pressure results in a corresponding increase in the deflection of the CNT. When the pressure distributed at the CNT surface is converted into a resultant force, it acts at the mid-point of the nanotube span. At that point, the shearing force will be zero while bending moment will be maximum. This results in an increase in CNT deflection. Furthermore, an increase in foundation parameter and temperature have an attenuating attribute on CNT response (Figures 2–4). 

Figure 2 Influence of uniformly distributed pressure on deflection.

Figure 3 Influence of temperature on CNT deflection.

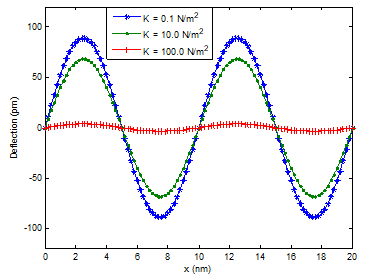
Figure 4 Influence of foundation on CNT deflection.

Figure 5 First mode dynamic response of CNT.

Figure 6 Second mode dynamic response of CNT.

Figure 7 Third mode dynamic response of CNT.

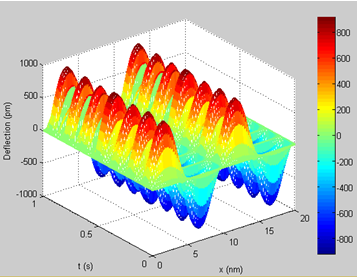
Figure 8 Forth mode dynamic response of CNT.

Dynamic response of the SWCNT

Figures 5–8 illustrate the multi-dimensional dynamic response of the CNT for different modes. The transient responses depict the possibility of tracking the behaviour of the CNT at any instance. This analysis is vital as it helps in the monitoring and adjustment of the CNT during use. 

The Shear force and bending moment of the SWCNT

Figures 8–12 depict the multi-dimensional Shearing force and bending moment diagram of the CNT for bi-modal cases. Locations with maximum bending moments are observed to possess minimum shear force. The combination of these responses and the mode shape of the structure may be used to track location of anti-nodes for resonance prevention.

Figure 9 First mode shear force of CNT.

Figure 10 Second mode shear force of CNT.

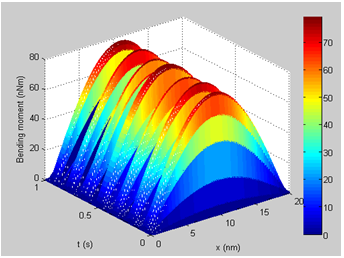
Figure 11 First mode Bending moment of CNT.

Figure 12 Second mode Bending moment of CNT.

Validation

The present study is also reduced and compared with those of previous studies with good agreements established as demonstrated below (Table 3):

In this paper, analytical investigations of dynamic response of a CNT exposed to an external uniform pressure has been carried out using TDTM. The exact solution as presented in this work are verified numerically and validated using results from previous studies. It was established that the TDTM gives a good result and is efficient for the problem investigated. Based on the study, the following include some of the conclusions derived;

1. Increase in surrounding pressure increases nanotube deflection.
2. Bending moment is minimum at locations of maximum shear forces
3. Increase in temperature and foundation parameters attenuates vibration
4. TDTM is efficient for the problem investigated.

The authors acknowledge the Faculty of Engineering, University of Lagos for the data provided towards the achievement of this work.

None.

1. S Iijima. Helical micro tubes of graphitic carbon. Nature. 1991;354:56–58.
2. M Terrones, F Banhart, N Grobert, et al. Molecular junctions by joining single–walled carbon nanotubes. Phys Rev Lett. 2002;89:07550.
3. P Nagy, R Ehlich, LP Biro, et al. Y–branching of single walled carbon nanotubes. Appl Phys A Mater. 2000;70:481–483.
4. LA Chernozatonskii. Carbon nanotubes connectors and planar jungle gyms. Appl Phys A. 1992;172:173–176.
5. KM Liew, CH Wong, XQ He, et al. Nanomechanics of single and multiwalled carbon nanotubes. Physical Review. 2004;B69.
6. A Pantano, MC Boyce, DM Parks. Mechanics of axial compression of single and multi–wall carbon nanotubes. Journal of Engineering Materials and Technology. 2004;126:279–284.
7. A Pantano, DM Parks, MC Boyce. Mechanics of deformation of single– and multi–wall carbon nanotubes. Journal of the Mechanics and Physics of Solids. 2004;789–821.
8. D Qian, GJ Wagner, WK Liu, et al. Mechanics of carbon nanotubes. Applied Mechanics Reviews. 2002;55:495–533.
9. JP Salvetat, JM Bonard, NH Thomson, et al. Zuppiroli, Mechanical properties of carbon nanotubes. Applied Physics. 1999;255–260.
10. A Sears, RC Batra. Buckling of carbon nanotubes under axial compression. Physical Review. 2006:B73.
11. J Yoon, CQ Ru, A Mioduchowski. Et al. Noncoaxial resonance of an isolated multiwall carbon nanotube. Physical Review. 2002:B66.
12. X Wang, H Cai, Effects of initial stress on non–coaxial resonance of multi–wall carbon nanotubes. Acta Materialia. 2006;54:2067–2074.
13. CM Wang, VBC Tan, YY Zhang, et al. Timoshenko beam model for vibration analysis of multi–walled carbon nanotubes. Journal of Sound and Vibration. 2006;294:1060–1072.
14. Y Zhang, G Liu, X Han. Transverse vibrations of double–walled carbon nanotubes under compressive axial load. Physics Letters. 2005;A340:258–266.
15. I Elishakoff, D Pentaras. Fundamental natural frequencies of double–walled carbon nanotubes. Journal of Sound and Vibration. 2009;229:652–664.
16. E Buks, B Yurke. Mass detection with nonlinear nanomechanical resonator. Physical Review E74. 2006.
17. HWC Postma, I Kozinsky, A Husain, et al. Dynamic range of nanotube– and nanowire–based electromechanical systems. Applied Physics Letters. 2005;86.
18. YM Fu, JW Hong, XQ Wang. Analysis of nonlinear vibration for embedded carbon nanotubes. Journal of Sound and Vibration. 2006;296:746–756.
19. KY Xu, XN Guo, CQ Ru. Vibration of a double–walled carbon nanotube aroused by nonlinear intertube van der Waals forces, Journal of Applied Physics. 2006; 99.
20. M Dequesnes, Z Tang, NR Aluru. Static and dynamic analysis of carbon nanotube–based switches. Transactions of the ASME. 2004;126:230–237.
21. HM Ouakad, MI Younis. Nonlinear dynamics of electrically actuated carbon nanotube resonators. Journal of Computational and Nonlinear Dynamics. 2010:5.
22. M Zamanian, SE Khadem, SN Mahmoodi. Analysis of non–linear vibrations of a microresonator under piezoelectric and electrostatic actuations. Journal of Mechanical Engineering Science. 223;2009:329–344.
23. EM Abdel–Rahman, AH Nayfeh. Secondary resonances of electrically actuated resonant microsensors. Journal of Micromechnics and Microengineering. 2003;13:491–501.
24. MA Hawwa, HM Al–Qahtani. Nonlinear oscillations of a double–walled carbon nanotube. Computational Materials Science. 2010;48:140–143.
25. A Hajnayeb, SE Khadem. Nonlinear vibration and stability analysis of a double–walled carbon nanotube under electrostatic actuation. Journal of Sound and Vibration. 2012;331:2443–2456.
26. A Belhadj, A Boukhalfa, S Belalia. Carbon Nanotube Structure Vibration Based on Non local Elasticity. Journal of Modern Materials. 2016;3(1):9–13.
27. Lei XW, Natsuki T, Shi JX, et al. Surface effects on the vibrational frequency of double–walled carbon nanotubes using the nonlocal Timoshenko beam model. Composites Part B. 2012;43:64–69.
28. SP Ashgharifard, YM Haeri. Nonlinear free vibrations of functionally graded nanobeams with surface effects. Composites Part B. 2013;45:581–586.
29. L Wang. Vibration analysis of fluid–conveying nanotubes with consideration of surface effects. Physica E. 2010;43:437–439.
30. LP Biro, ZE Horvat, GI Mark, et al. Carbon nanotube Y junctions: growth and properties, Diamond and Related Materials. 2004;13:241–249.
31. RM Lin. Nanoscale vibration characterization of multi–layered graphene sheets embedded in an elastic medium. Computational Materials Science. 2012;53:44–52.
32. SC Pradhan, JK Phadikar. Small scale effect on vibration of embedded multilayered graphene sheets based on nonlocal continuum models. Physics Letters A. 2009;373:1062–1069.
33. AA Ghorbanpour, MS Zarei, S Amir, et al. Nonlinear nonlocal vibration of embedded DWCNT conveying fluid using shell model. Physica B. 2013;410:188–196.
34. AA Ghorbanpour, S Amir. Electro–thermal vibration of visco–elastically coupled BNNT systems conveying fluid embedded on elastic foundation via strain gradient theory. Physica B. 2013;419:1–6.
35. A Eichler, J Moser, J Chaste, et al. Nonlinear damping in mechanical resonators made from carbon nanotubes and grapheme. Nature Nanotechnology. 2011;6:339–342.
36. HL Dodds, H Runyan. Effects of high velocity fluid flow in the bending vibrations and static divergence of a simply supported pipe. National Aeronautical and Space Adminitration Report, NASA TN. 1965;D–2870.
37. AA Yinusa, MG Sobamowo. Thermal Instability and Dynamic Response Analysis of a Tensioned Carbon Nanotube under Moving Uniformly Distributed External Pressure. Nano Materials Science. 2019;1–21.
38. AA Yinusa, MG Sobamowo, AO Adelaja. Nonlinear Vibration Analysis of an Embedded Branched
    Nanofluid–Conveying Carbon Nanotube: Influence of Downstream Angle, Temperature Change and Two
    Dimensional External Magnetic field. Nano Materials Science. 2019;1–18.
39. F Liu, RM. Wagterveld B, Gebben MJ, et al. Carbon nanotube yarns as strong flexible conductive capacitive electrodes. Colloids. 2014;3:9–12. 
40. MG Sobamowo, AA Yinusa. Thermo–fluidic parameters effects on nonlinear vibration of fluid–conveying nanotube resting on elastic foundations using Homotopy Perturbation method. Journal of Thermal Engineering. 2018;4(4):2211–2233.
41. SB Coşkun, MT Atay, B Öztürk. Transverse Vibration Analysis of Euler–Bernoulli Beams Using Analytical Approximate Techniques. Advances in Vibration Analysis Research, 2011.
42. MG Sobamowo, AA. Yinusa. Power Series –After treatment Technique for Nonlinear Cubic Duffing and Double–Well Duffing Oscillators. 2017;48(2):297–306.