Glacial till, a broadly graded soil formed by the action of glaciation, is used in many parts of the world as dam core material. Statistically these show higher frequency of internal erosion incidents in dams than other types of core soils. One mechanism that may be influential is suffusion as caused by internal instability, which is one initiation mode of internal erosion. A compilation of 23 laboratory tests on suffusion of glacial till core soil has been compiled of which 13 performed unstable. An assessment of the potential for internal instability is made using five empirical methods that evaluates the shape of the particle size distribution. Evaluation of the database indicates on the methods’ applicability to glacial till gradations, and, furthermore, it reveals that the Kenney-Lau approach and its Li-Fannin adaptation provide predictions relatively more accurate in identifying unstable gradations due to suffusion. A stricter assessment is suggested by extending the Li-Fannin adaptation so that it incorporates a transition zone defined by the range 0.68≤H/F<1.0.

Keywords: dams, erosion, glacial soils, gravels, sands, silts

D             grain size (mm)

F              mass passing at grain size D (%)

H             mass increment between D and 4D (%)

F_f             finer fraction

C_u           coefficient of uniformity, C_u=D₆₀/D₁₀

(H/F)_min  stability index, defined by the smallest value of H/F, for 0 <F≤20 % in soil with a widely-graded coarse fraction

FC#4      percentage fines content of base soil passing the No. 4 sieve (4.75mm)

F#200       percentage fines content (< #200 sieve, 0.075mm) of full sample of soil

Δm/m     mass loss in seepage test (%)

GBE       global backward erosion

Glacial till is used in many parts of the world as impervious core material in embankment dams. This type of soil has been found to be quite susceptible to internal erosion,^1–3 especially if compared to other types of soils used as core materials in dams.⁴ Its susceptibility to suffusion, which stems from the erodibility of the soil itself, is still relatively unexplored. Its vulnerability to backward erosion and filter incompatibility, however, which heretofore perhaps considered its main culprit for internal erosion, has been shown in many laboratory tests.^1,3,5–9 In terms of suffusion, although only a few studies are available, laboratory tests have shown that glacial till may be susceptible.^7,10-13 Internal erosion is initiated by the mechanisms of concentrated leak erosion, backward erosion, contact erosion, and suffusion erosion.¹⁴ Backward erosion occurs at a free unfiltered surface or at the interface to an inadequate coarse filter.¹⁴ It works itself progressively backward towards the source of water by the detachment of soil particles. Assisted by gravity, it can cause near-vertical pipes in the dam body, which is called global backward erosion (i.e., GBE).¹⁴ Suffusion, on the other hand, occurs inside of a fixed bulk volume of a core soil or dam zone, and due to internal instability of the gradation it erodes the finer fraction through the constrictions of its coarser fraction.¹⁴

In the current study a database consisting of 23 glacial till gradations from laboratory tests are compiled and analysed. Two approaches are used to assess the potential internal instability and thus susceptibility to suffusion, namely the empirical methods of Kenney & Lau^15,16 and its adaption by Li & Fannin¹⁷ & Burenkova¹⁸ and its adaptations by Wan & Fell^19,20 Glacial till soils are strictly speaking outside the extent of the methods, in general sand and gravel gradations were tested, so evaluation of the database herein indicates on the one hand the applicability of these methods. On the other, it will show that an improved assessment can be made by extending the Li-Fannin adaptation by incorporating a transition zone defined by the range 0.68≤ H/F<1.0.

In Rönnqvist & Viklander²¹ five laboratory studies on the mechanism of suffusion of glacial till soils were reviewed (i.e., studies by Lafleur & Nguyen¹¹ & Wan¹⁰ & Moffat et al²² & Hunter et al⁸ & Lilja et al.⁷ In these, there were 11 gradations of glacial till in total. In addition, Rönnqvist¹³ performed suffusion tests on 4 glacial tills from the core or borrow area of four Swedish dams and eight mixtures with varied gravel content based on these tills. The total compilation yields thus an experimental database that includes 23 gradations (Figure 1). Their grading characteristics are given in Table 1, which reveals an extent of fines content from 4%<F#200<38% and 6<C_u<600. 13 gradations were reportedly internally unstable according to laboratory tests (i.e., S7, S10, C-20, C-30, CG3, Mr3, Mr19, BE3, BE4, GR2, GR3, ST2 and ST3), exhibiting change in grading characteristics after the test or experiencing seepage- or pore water pressure variations indicative of instability during test. However, specimens CG3, GR2 and ST2 ultimately failed by GBE, and nine have potentially a finer fraction that exceeds 35% (i.e., gradations S17, S28, RD, FG1, Mr19, BE1, RA1, GR1, ST2, thus, possibly eliminating these from suffusion susceptibility. However, it is reasonable to suggest that the failure process of CG3 and GR2 were affected by suffusion given their potential for grading instability.

Figure 1 Compilation of 23 glacial till gradations used in laboratory suffusion tests.

Analysis using empirical methods

In the internally unstable gradation, the finer fraction (i.e., F_f) under-fills the coarser fraction thus creating fixed coarser particles and mobile finer particles.¹⁴ However, unless F_f<≈35 % of the total soil it is probably not susceptible to suffusion.^15,19,23 An excessive F_f means the soil is matrix-supported and its coarser particles are floating in the finer fraction, thus eliminating suffusion. It can still be vulnerable to backward erosion. The finer fraction of a gradation is usually defined as the point of inflection of the particle size distribution.¹⁴ Results of the empirical analyses are summarised below.

The Kenney-Lau method and Li-Fannin adaptation

The potential for internal instability can be evaluated according to Kenney & Lau^15,16 from a shape analysis over a designated portion of the finer end of the gradation curve, which for widely-graded materials (i.e., C_u>3) is defined by the evaluation range of F≤20%. Skempton & Brogan²³ introduced the stability index (i.e., (H/F)_min) from the minimum value along the Kenney-Lau H:F shape curve. Li & Fannin¹⁷ adapted the method to incorporate the Kezdi²⁴ split-gradation method. They found that the Kenney-Lau method become less conservative over the coarser end of the evaluation range (F=15-20%) by shifting to the Kezdi criterion. Gradation analyses established the stability index, (H/F)_min of all 23 gradations (Figure 2) and the results are summarized in Table 2, which shows that the Kenney-Lau method determines:

Figure 2 Summary of gradation analyses: the Kenney & Lau^15,16 method and the Li & Fannin¹⁷ adaptation.

1. 9 of the 13 unstable gradations (69 %) have a potential for internal instability; and,
2. 56 % of all gradations deemed potentially unstable performed unstable.

Thus, the Kenney-Lau method exhibits a 69% success rate in identifying the unstable gradations and 56% accuracy. However, if potentially irrelevant gradations are disregarded, i.e., gradations with F_f>35% or that failed by backward erosion (GBE), it leaves 12 gradations; the Kenney-Lau method then identifies 78% of the unstable gradations with 78% accuracy. The Li-Fannin adaptation provides comparably more accurate predictions by 88% accuracy (Table 2) when excluding potentially irrelevant gradations.

The Burenkova method and Wan-Fell adaptation

Burenkova¹⁸ proposed that the potential for internal instability be evaluated from “conditional factors of uniformity” determined for the slope of the coarser fraction by D₉₀/D₆₀ and for the overall slope of the gradation curve by D₉₀/D₁₅. Subsequently Wan & Fell1⁹ adapted the method for widely graded soils with limited clay and plasticity to incorporate a probabilistic approach. Gradation analyses of all 23 gradations (Figure 3) and the results are summarized in Table 2, which shows that the Burenkova method determines:

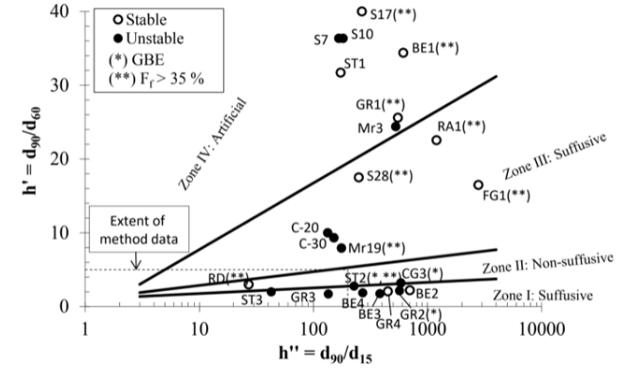
Figure 3 Summary of gradation analyses: the Burenkova¹⁸ method.

1. 8 of the 13 unstable gradations (62 %) locate in Zones I or III and have a potential for internal instability; and,
2. 62 % of all gradations deemed potentially unstable performed unstable.

Thus, the Burenkova method exhibits a 62% success rate in identifying the unstable gradations and 62% accuracy. By disregarding potentially irrelevant gradations the accuracy of the Burenkova method increases to 75% (Table 2). Whereas the Wan-Fell adaptation has an accuracy of 67% but lower success rate (44%), when excluding potentially irrelevant gradations (Figure 4). Potential for internal instability is for the Wan-Fell adaptation set at greater than 5% probability of internal instability.

Figure 4 Summary of gradation analyses: the Wan & Fell¹⁹ (2004) adaptation.

The wan-fell alternative method

Wan & Fell²⁰ discovered that potential for internal instability in soils with a steeply sloped coarse fraction and flat finer fraction are better evaluated by a value of D₂₀/D₅ for the finer fraction and the same characteristic D₉₀/D₆₀ value for the coarser fraction. Gradation analyses of all 23 gradations (Figure 5) and the results are summarized in Table 2, which shows that the Wan-Fell alternative method determines:

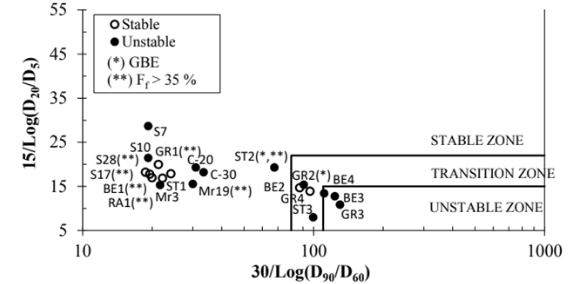
Figure 5 Summary of gradation analyses: the Wan & Fell²⁰ alternative method.

1. 5 of the 12 unstable gradations (unstable CG3 not included due to insufficient gradation data) (42 %) locate in the unstable or transition region and have a potential for internal instability; and,
2. 71% of all gradations deemed potentially unstable performed unstable.

The Kenney & Lau^15,16 method has been tested in several studies tests in the literature^10,20 and although, strictly, widely graded soil with fines is outside of the method’s extent of data, there are studies suggesting validity.^12,22,25,26 Consider the laboratory tests of Rönnqvist¹³addressed in this study (Figure 8): specimens BE1, BE2, RA1, GR1 and GR4 are potentially internally unstable obtaining (H/F)_min<1, but performing without instability in the tests. This suggests that the Kenney-Lau boundary of H/F=1 over-predicts instability in glacial till gradations. Indeed, in reviewing the Kenney-Lau method, Rönnqvist & Viklander²⁷ found H/F=1 slightly conservative since the boundary does not encompass all stable gradations included in the Kenney-Lau data. By plotting stability index against erosion loss (Δm/m) of the Rönnqvist¹³ tests, decreasing internal stability yields increasing erosion loss as indicated by the best-fit power trendline of the specimens with F_f<35% (those potentially susceptible to suffusion) (Figure 6). The unstable specimens exhibits (H/F)_min<0.68 and (Δm/m)>5 %, whereas the stable (H/F)_min≥0.68. ST2 deviates due to GBE. Also, by plotting the stability index before the test (i.e., pre-test) against after (i.e., post-test) a gradually more severe shift in grading characteristics can be seen at lower stability indices (Figure 7) (as indicated by the polynomial trendline). The post-test gradation data on d < 0.063 mm of ST1, ST2 and RA1 has been assumed equal to their initial, pre-test, gradation.

Figure 6 Stability index (H/F) min in relation mass loss (power trendline is established for samples with Ff<35 %).

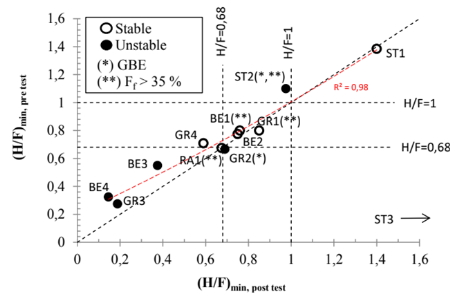
Figure 7 Stability index (H/F) min pre-test versus post-test (polynomial trendline is established for samples with Ff < 35 %. (ST3 not considered).

Figure 8 Compilation of H:F shape curves in relation to a transition zone 0.68≤H/F<1.0.

In the range 0.68≤(H/F)_min<1.0 there is some intermixing around the line of unity (i.e., (H/F)_pre=(H/F)_post) suggesting a transition zone. More data is needed for a further analysis, nevertheless, the plotting positions of the stability indices (i.e., (H/F)_min) of the 23 gradations in this study (Figure 8) corroborates the possibility of an improved delineation between stable and unstable gradations in the Kenney-Lau H:F space. Indeed, by introducing the transition zone 0.68≤H/F<1.0 the stable gradations, previously deemed potentially unstable, locate in the transition zone (i.e., gradations GR4 and RA1) (Figure 8). Furthermore, by analysing stability indices (H/F)_min only, there is a risk of overlooking that a gradation exhibits potential instability along the H:F-shape curve. Consider gradation BE2: the stability index analysis for BE2 suggests stability according to the Li-Fannin adaptation, which agrees with the test performance, however, the shape of the BE2 gradation preceding the (H/F)_min=0.78 at F=20% is in the Kenney & Lau¹⁶ unstable zone H/F<1.0 beyond F≈11% (Figure 7). For BE2 this indicates instability over this range which contradicts its performance, suggesting there is a transition zone. Relevant also for specimen RA1 (although this specimen may not have been susceptible to suffusion due to excessive finer fraction) and specimen GR4 (Figure 8). Figure 8 shows the stability indices (H/F)_min plotted in the H:F-space, against the modified Li-Fannin adaptation with transition zone 0.68≤H/F<1.0. Although it fails to identify the unstable gradation C-30 the modified method’s success in identifying unstable gradations is slightly reduced to 67 % compared to the Kenney-Lau method, but the accuracy improves to 100 % (when excluding the potentially irrelevant gradations) (Table 2).

23 gradations of glacial till have been evaluated in this paper of which 13 have performed unstable. Five empirical methods for the evaluation of potential for internal instability have been applied on the gradations. Evaluation suggests that the approach by Kenney-Lau for shape analysis of the gradation curve, and its Li-Fannin adaptation, provide predictions relatively more accurate in identifying unstable gradations due to suffusion. A stricter assessment is suggested for this type of soil by modifying the Li-Fannin method so that it incorporates a transition zone defined by the range 0.68≤H/F<1.0, indeed, 80 % of the gradations deemed potentially unstable with the modified method did perform unstable. However, in the design or specification of gradations using the Kenney & Lau¹⁶ method, a relaxation from the original H/F=1 boundary is not recommended.

The research presented was carried out as part of ”Swedish Hydropower Centre - SVC”. SVC has been established by the Swedish Energy Agency, Energiforsk and Svenska Kraftnät together with Luleå University of Technology, the Royal Institute of Technology, Chalmers University of Technology and Uppsala University.

The authors declare that there is no conflict of interest.

1. Ravaska O. Piping susceptibility of glacial till. Florence Proc 19th ICOLD Congress; 1997:455–
2. Sherard JL. Sinkholes in dams of coarse, broadly graded soils. Proc 13th ICOLD Congress; 1979:25–35.
3. Foster MA. The probability of failure of embankment dams by internal erosion and piping. The University of New South Wales; 1999.
4. Foster M, Fell R, Spannagle M. The statistics of embankment dam failures and accidents. Canadian Geotechnical Journal. 2000;37:1000–1024.
5. Sherard JL. Filters for glacial tills and other coarse impervious soils. Memorandum 1G, Unpublished reports of filter research carried out in the Lincoln, Nebraska, Soil Conservation Service Soil Mechanics Laboratory. 1984.
6. Sherard JL, Dunnigan LP. Critical filters for impervious soils. Journal of Geotechnical Engineering. 1989;115(7): 927–947.
7. Lilja HM, Rother M, Ravaska OT. Filter material study for an earth dam project. In: Dam Safety, editor. Balkema. 1998:825–
8. Hunter G, Fell R, Topham C. Backward erosion piping: what are the chances of that? Proc Australian National Committee on Large Dams 2012; Perth. 2012.
9. Lafleur J, Mlynarek J, Rollin AL. Filtration of broadly graded cohesionless soils. Journal of Geotechnical Engineering. 1989;15(12):1747–1768.
10. Wan CF. Experimental investigations of piping erosion and suffusion of soils in embankment dams and their foundations. Sydney, Australia. The University of New South Wales; 2006.
11. Lafleur J, Nguyen PH. Internal stability of particles in dam cores made of cohesionless broadly graded moraines. Internal Erosion of Dams and their Foundations. 2007:151–158.
12. Moffat R, Fannin RJ. A hydromechanical relation governing internal stability of cohesionless soil, Canadian Geotechnical Journal. 2011;48:413–424.
13. Rönnqvist H. On the assessment of internal erosion of dam cores of glacial till. Luleå, Sweden. Luleå University of Technology; 2015.
14. Internal erosion of existing dams, levees and dykes, and their foundations. Bulletin 164, Paris France. 2017.
15. Kenney TC, Lau D. Internal stability of granular filters. Canadian Geotechnical Journal. 1985;22(2):215–225.
16. Kenney TC, Lau D. Internal stability of granular filters: Reply. Canadian Geotechnical Journal. 1986;23: 420–
17. Li M, Fannin RJ. Comparison of two criteria for internal stability of granular soil. Canadian Geotechnical Journal. 2008;45:1303–
18. Burenkova VV. Assessment of suffusion in non-cohesive and graded soils. In: Brauns Heibum, Schuler editors. Filters in geotechnical engineering. Proc. First International Conference “Geo-Filters; Rotterdam, Balkema. 1993:357–
19. Wan CF, Fell R. Experimental investigation of internal instability of soils in embankment dams and their foundation. UNICIV report No 429. The University of New South Wales; 2004.
20. Wan CF, Fell R. Assessing the potential of internal instability and suffusion in embankment dams and their foundations. Journal of Geotechnical and Geoenvironmental Engineering. 2008;134(3):401–407.
21. Rönnqvist H, Viklander P. Laboratory testing of internal stability of glacial till, a review. Electronic Journal of Geotechnical Engineering. 2014a:19:6315–6336.
22. Moffat R, Fannin RJ, Garner S. Spatial and temporal progression of internal erosion in cohesionless soil. Canadian Geotechnical Journal. 2011;48:399–412.
23. Skempton AW, Brogan JM. Experiments on piping in sandy gravels. Géotechnique. 1994;44:449–460.
24. Kezdi A. Soil physics – selected topics. Amsterdam. Elsevier Scientific Publishing; 1979.
25. Li M, Fannin RJ, Garner SJ. Application of a New Criterion for Assessing the Susceptibility to Internal Erosion. Canadian Dam Association; 2009.
26. Rönnqvist H, Viklander P. Extending the Kenney-Lau method to dam core soils of glacial till. Geotechnical Research. 2014b;1:73–87.
27. Rönnqvist H, Viklander P. On the Kenney-Lau approach to internal stability evaluation of soils. Geomaterials. 2014c;4:129–140.