Carbon diffusion in metals has received a lot of attention and has been the subject of intensive theoretical investigations in recent years. The purpose of this work is development a simple statistical model of the carbon atoms diffusion in the crystal lattice of metals and its application for calculating the diffusion coefficients of carbon atoms in iron and steel. The relationship between the diffusion flux of atoms and the gradient of their chemical potential, as required by non-equilibrium thermodynamics, is obtained from the basic principles of statistical thermodynamics. For a real solid solution of impurity atoms in a metal, an expression is found for the diffusion coefficient, the value of which depends on physical constants, the atomic weight of the solute, the square of the temperature and activity i-element in solid solution. The calculations have a good agreement with the known experimental data on the diffusion of carbon atoms in iron and steels and is higher than in classical atomic diffusion models. The activation energy of carbon diffusion in γ- phase of various steels has values close to 120 kJ. Proposed formula well describes the deviation of the carbon diffusion coefficient from the Arrhenius law at medium and high temperature.

Keywords: steels, statistical thermodynamics, carbon diffusion, activity, pre-exponential factor, activation energy, γ- phase

Carbon diffusion in metals has received a lot of attention and has been the subject of intensive theoretical investigations in recent years.^1,2 First, this is due to the practical interest in using the Fe – C system for a number of technological applications, including the creation of radiation-resistant materials, high-hardness tool steels, and in automotive applications.^1–4

Secondly, carbon diffusion in Fe and Fe alloys is very important because this leads to engineering problems associated with carbides formation and degradation of high strength steels, reactor materials, etc.^5,6

Diffusion of interstitial carbon atoms in iron is the rate-limiting phenomenon of a number of phase transitions in body-centered (bсc) and body-centered tetragonal (bct) phases such as ferrite and martensite.⁷ To quantify the effect of diffusion elements on phase transformation, multi-scale modeling is required.⁸ The numerical tools that are applied include ab initio solutions to the Schroodinger equation, fitting of effective many-body interaction potentials, molecular dynamics simulation, Monte Carlo simulation of defect evolution, phase-field modeling and quasicontinuum rate theory.^8–15 These methods are often very complex and have their limits of their applicability for modeling steels and alloys.¹⁴

In iron crystals, carbon atoms are in interstitials and in the diffusion process they pass from one interstitial site to another. In FCC lattice, carbon can occupy octahedral type of interstitial sites⁷ but also diffuse through the tetrahedral type of interstitial sites. At the present time, the question of the carbon diffusion mechanism in the crystal lattice of iron remains. Even in a pure crystal, transitions between interstitials of different types are possible, which entails, in particular, the ambiguity of the activation energy of carbons diffusion. In addition, as noted in,⁷ the redistribution of carbons atoms in interstitial sites due to changes in external conditions, for example, deformation, can lead to a change in the diffusion parameters. It should be noted that other factors may also lead to deviations from the Arrhenius law, in particular, the possibility of diffusion jumps of different lengths and the effect of crystal lattice defects.^10,15

First principles calculations and classical approaches molecular mechanics has been used to study carbon diffusion energy in the case of body-centered cubic (BCC) Fe in several papers.^7,10,13,16

It is assumed that modern ab initio modeling will provide a good description of the geometry, energy, and potential energy surface in Fe-C - systems. However, as far as we know, there is no systematic derivation of the diffusion coefficients for which quantum-statistical effects are taken into account in a wide temperature range. The use of such calculations is important for understanding the possible mechanisms of hydrogen diffusion in metalls.

The purpose of this work is development a simple statistical model of the diffusion of carbon atoms in the crystal lattice of metals and its application for calculating the diffusion coefficients of carbon atoms in iron and steel.

The classical atomic theory of diffusion gives an expression for the diffusion coefficient self-diffusion. In early works on the statistical theory Ya. I. Frenkel and his followers, the dependence of the diffusion coefficient on the square of the distance between two atomic positions was obtained.^17,18 This expression for the diffusion coefficient is also commonly used in modern molecular dynamics.^19,20 However, due to a significant discrepancy between the calculated and experimental data, even in these classical works, additional parameters were introduced to calculate the diffusion coefficients.

At the same time, it is well known, that the main driving forces of diffusion in non-equilibrium thermodynamics are the gradients of chemical potentials μ_i of the components of the system.^18,21 This position should be taken into account when deriving equations for the diffusion coefficient. However, it is very difficult to introduce chemical potentials into the diffusion equations in the atomic statistical model.

In solid state physics for the analysis of multicomponent systems - solid solutions, etc. - long and widely used methods of statistical physics,^21,22 in particular, thermodynamics. In statistical thermodynamics, equations describing thermionic emission have long been known.²²

To describe the diffusion of atoms in the crystal lattice of a metal in work²³ was created the statistical model of diffusion. Large attractive forces hold atoms in the crystal lattice of a metal; therefore, the potential energy of moving, i.e. diffusing atoms is greater than the potential energy of the atoms of the crystal lattice by the value of U - the activation energy of the diffusion process.

We can select out in a unit volume of metal V a unit surface perpendicular to the x axis (Figure 1).

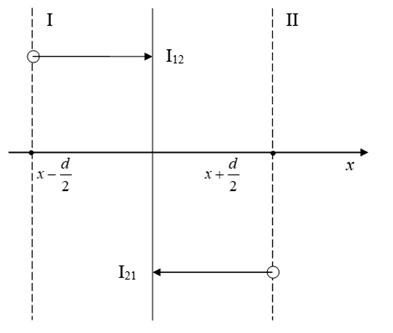
Figure 1 Scheme of diffusion in the statistical atomic model.¹⁸

The total flux of diffusing atoms in the positive direction of the x-axis is equal to the difference in the flux I₁₂ (from the plane x – d/2 to the plane x + d/2) and I₂₁ (in the opposite direction).¹⁸

Only those metal atoms for which the energy ε is larger than the potential barrier of the lattice u can pass through this surface in the positive direction of the x axis:$\epsilon =\frac{{\text{p}}_{\text{x}}^{\text{2}}}{\text{2m}}\ge u$   (1) and m is the mass of the diffusing atom.

The diffusion flux I₁₂ is determined by the number of metal atoms or impurities passing through a unit of surface per unit of time. To find its expression, it is necessary to calculate the distribution of atoms by impulses.

The number of states, whose impulse components are in the range of values ​​between p_x and p_x + dp_x, p_y and p_y + dp_y, p_z and p_z + dp_z is equal to^21,22:

$\frac{d\Gamma }{h^3}=\frac{\text{V}d{p}_{x}d{p}_{y}d{p}_z}{h^{\text{3}}}$   (2)

h – Plank constant.

We will assume that the number of diffusing atom in each state is determined by the Boltzmann distribution²¹:

$N_i=\frac{1}{\exp (({\epsilon }_i-\mu )/kT)}$   (3)

T – Temperature, μ is the chemical potential of diffusing atoms, k – Boltzmann's constant. When

$dN=\frac{\text{V}d{p}_{x}d{p}_{y}d{p}_z}{{\text{h}}^{\text{3}}\exp ((\epsilon -\mu )/kT)}$   (4)

There dN is the number of diffusing atoms in the metal whose pulse components are in the range of values ​​between p_x and p_x + dp_x, p_y and p_y + dp_y, p_z and p_z + dp_z, i.e. number of particles with impulse and energy given in magnitude and direction:   

$\epsilon =\frac{p_x^2+p_y^2+p_z^2}{\text{2m}}$   (5)

We find now the number of atoms passing through a unit of surface per unit of time.²² We direct the x axis perpendicular to the surface under consideration (Figure 2).

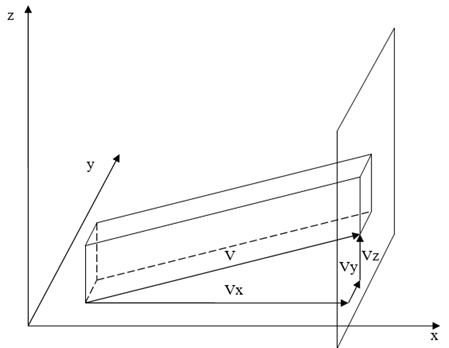
Figure 2 Scheme for determining the flux of particles through a single site in the direction of the x axis.²²

Having performed calculations for the diffusion flux of atoms, similar to the calculations of the thermionic emission current,²² was find the diffusion flux I₁₂ in the direction of the x axis²³:

$I_{12}=\frac{2\pi m{k}^2{T}^2}{h^3}{\text{e}}^{\text{-(U-}{\mu }_{\text{1}}\text{)/kT}}$   (6)

Where μ₁ is the chemical potential of diffusing atoms on the side of plane I (Figure 1).

Similarly, was find the diffusion flux I₂₁, where μ₂ is the chemical potential of diffusing atoms on the side of plane II. The total diffusion flux is equal to:

$Ic=I_{12}-I_{21}=\frac{2\pi m{k}^2{T}^2}{h^3}{\text{e}}^{\text{-w/kT}}\text{(}1\text{-exp(}\Delta \mu \text{/kT)) }$   (7)

Where μ₂ is the chemical potential of diffusing atoms on the side of plane II, w=U-μ₁, Δμ=μ₂ – μ₁. Chemical potential of diffusing atoms on the side of plane I is taken as the base.

Equation (7) is the most general formula of the statistical model for the diffusion flux of atoms in the crystal lattice.²³ If the diffusion of an element occurs from one phase to another, the chemical potentials of which differ sharply, then it is the exact expression (7) that should be used. If we consider the diffusion of atoms in the single-phase region, then the difference of their chemical potential at the interplanar distance d: |Δμ| << kT, then exp(Δμ/kT)≈1+Δμ/kT. According to the average theorem, can find:

$Ic=-\frac{2\pi mkTd}{h^3}{\text{e}}^{\text{-w/kT}}\frac{\partial \mu }{\partial х}$   (8)

It is the statistical equation of atoms diffusion in a crystal lattice of a metal. It directly shows that the diffusion flux of atoms directly depends on the gradient of the chemical potential, as it should be in a consistent thermodynamic theory.^2,18 In this case, equation (8) is the limiting case of equation (7) of the simple statistical model.

Using equation (8) allows us to calculate ab initio the pre-exponential factor of atoms diffusion in a crystal lattice of a metal.²³ Expression (8) has the dimension of particles/(m²ˑs). For that. In order for the flow to have the dimension mol/(m²·s), we divide its value by the Avogadro number N.

It is understood that the atoms of the diffusing element fill the entire volume. For alloying elements in expression (2), instead of the volume V, their partial volume in the alloy should be substituted, equal to:

$V_i=V·C_i$   (9)

Where C_i is content of i - element in an alloy in atomic parts.

If we further consider the real solid solution of the atoms of a substance in a metal, then we can write the following expression for element i ¹⁸:

${\mu }_i={\mu }_i{}^0(Т)+ kTln{a}_i$   (10)

Where $a_i={\gamma }_i\cdot c_i$   (11)

a_i - activity, γ_i - activity coefficient of element i in solid solution.

Whence

$\frac{\partial \mu }{\partial х}=\frac{kT}{a_i}\frac{\partial a_i}{\partial x}$   (12)

Substituting expression (9) - (12) into (8), we find diffusion flux of i-th element in solid solution:

$I_i=-\frac{2\pi C_i{m}_i{k}^2{T}^{2}d}{N{h}^3}{\text{e}}^{-\frac{\text{u}-{\mu }_0}{\text{kT}}}{\gamma }_i\frac{\partial c_i}{\partial х}$   (13)

(In equation (13) it is assumed that the activity coefficient γ_i does not depend on the x coordinate).

When the pre-exponential factor in our case is:

$D_0^i=\frac{2\pi C_i{m}_i{\gamma }_i{k}^2{T}^{2}d}{N{h}^3}$   (14)

We see that the diffusion coefficient depends at three points (k, N and h), in two parameters (m_i is the mass of the i-diffusive atom and d is the interplanar distance), the amount of substance in the volume C_i, their activity coefficient γ_i and temperature of the metal in square.

We write the mass of atoms of the diffusing element in the form of the expression:

$m=N_i·m_a$   (15)

Where N_i is the atomic number of the element;

m_a is the atomic mass unit.

We also take into account that N_m is related to the concentration of C_i by the expression:

$C_i=N_{mi}·N_i/\rho$   (16)

Where ρ is the alloy density.

N_mi is the number of moles of the diffusing element per unit volume.

Then the expression for the diffusion coefficient of the atoms of the dissolved element in the metal takes the form:

$D_0^i=\frac{2\pi m_a{k}^{2}d}{h^{3}N\rho }\cdot A_i\cdot N_i^2\cdot T^2$   (17)

Where A_i = γ_i· N_mi - activity element i in solid solution. The activity of this element is generally unknown and this parameter is need to be determined from experimental data on diffusion or performed calculations.

Expression (17) of the developed statistical model significantly differs from the expressions obtained in classical atomic models.^17,18 The interplanar distance d enters into this expression in the first degree. Nevertheless, this formula assumes the dependence of D₀ on the square of the atomic number of the diffusing element and the square of the diffusion temperature.

If we compare expression (17) with the classical formula for the diffusion coefficient^16–18:               

$D=K{\Delta }^2\nu$   (18)

Where Δ is the length of a single jump of an atom during diffusion, ν is the jump frequency of atoms, K – coefficient (usually 1/6); and in formula (17) we put that d = Δ, then for the jump frequency we can find:

$\nu =\frac{2\pi m{A}_i{N}_i^2{k}^2{T}^2}{K{h}^3\Delta \rho }{\text{e}}^{{\text{-W}}_0\text{/kT}}$   (19)

We propose to use this expressions (17) and (19) for a more accurate calculation of the carbon diffusion coefficients in molecular dynamics (MD)¹³ and centroid path-integral molecular dynamics (CMD).¹⁹ The parameters, calculated in this way, can be called the parameters of the statistical model (SM).²⁴ The classical expressions for calculating diffusion coefficients does not take into account the Boltzmann distribution of diffusive particles in energy. Therefor the parameters of the statistical model should be used to compare and evaluate the accuracy of both models – MD and CMD.

For practical calculations of multicomponent systems - steels in the developed statistical model (SM) the diffusion coefficient D we can calculate by the formula, following from (17):

$D=D_{0}exp(-U_0/RT)$   (20)

Where D₀ = A₀Т².

Let us perform the appropriate calculations for the diffusion of carbon in iron and steels and compare them with the experimental data given in (Table 1).^16,25

It was shown in¹⁶ that the diffusion of carbon in α-iron deviates from the Arrhenius equation, which is an additional indication of the dependence of D₀ on the diffusion temperature. Similar experimental results were also obtained.²⁵

The calculated data for diffusion parameters of atoms carbon in α-iron and steels, performed by formula (20), given in Table 2.

The data of Table 1 and Table 2 show that the diffusion of C in the γ -phase is slower than in the α-phase at the same temperatures. The activation energy of carbon diffusion in γ - phase of various steels has values close to 120 kJ, which can be used in the corresponding models for calculating the structure and properties.²⁶

This formula (20) well describes the deviation of the carbon diffusion coefficient from the Arrhenius law at medium temperatures, shown in Figure 3.

Figure 3 Comparison of calculated and experimental data for diffusion coefficient of carbon atoms in α-iron and steels (individual points are experimental data from works,^16,25 dotted lines are calculated data).

Separately, graphs were plotted for the diffusion coefficients of carbon in γ - phase of some steels (Figure 4).

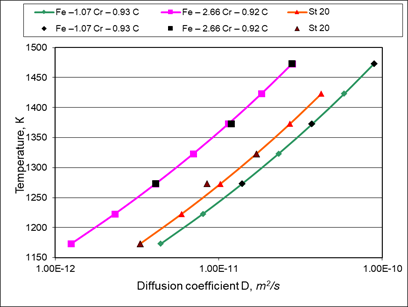
Figure 4 Comparison of calculated and experimental data for diffusion coefficient of carbon atoms in γ-phase of steels (individual points are experimental data from work,²⁵ dotted lines are calculated data).

As can be seen from the experimental data presented in Figure 4, the high-temperature diffusion of carbon in the γ-phase of steels corresponds to the Arrhenius equation to a much greater extent than diffusion in the α-phase. However, in this case, the proposed equation (20) gives a more accurate and adequate description of the carbon diffusion coefficients, shown in Figure 4.

Thus, a simple statistical model of the diffusion of impurity atoms in the crystal lattice of metals is developed in the article. The relationship between the diffusion flux of atoms and the gradient of their chemical potential, as required by nonequilibrium thermodynamics, is obtained from the basic principles of statistical thermodynamics. For an real solid solution of impurity atoms in a metal, an expression is found for the diffusion coefficient, the value of which depends on physical constants, the atomic weight of the solute, the square of the temperature and activity i-element in solid solution. The calculations are compared with the known experimental data on the diffusion of carbon atoms in iron and steels with a fairly good agreement between the results. This agreement for the given special cases of diffusion is higher than in classical atomic diffusion models.^17,18 Deviations from the Arrhenius law at high temperatures are also observed during the diffusion of C in W and Ta,²⁷ which can also be explained by the proposed statistical model.

Undoubtedly, this model does not take into account many specific factors affecting the diffusion parameters of carbons atoms in a metal, such as the interaction of impurity atoms and metal, the presence of vacancies, etc. Further development of this model will allow taking into account the influence of these factors on the diffusion of carbon in iron and steels.

This project was funded by the Swedish Foundation for Strategic Research (SSF), contract UKR22-0070. We acknowledge prof. Joakim Odqvist and prof. Annika Borgenstam from KTH Royal Institute of Technology for support.

None.

The authors have no conflicts of interest to declare that are relevant to the content of this article.

1. Sugianto A, Narazaki M, Kogawara M, et al. Numerical simulation and experimental verification of carburising–quenching process of SCr420H steel helical gear. Journal of Material Processing Technology. 2009;209(7):3597–3609.
2. Bobyr SV. Using the principles of nonequilibrium thermodynamics for the analysis of phase transformations in iron–carbon alloys. Chapter in the book "Non–Equilibirum Particle Dynamics", London: Intechopen; 2019. 134 p.
3. Zhang X, Hickel T, Rogal J, et al. Structural transformations among austenite, ferrite and cementite in Fe–C alloys: A unified theory based on ab initio simulations. Acta Materiala. 2015;99:281–289.
4. Jovičević–Klug P, Podgornik B. Review on the effect of deep cryogenic treatment of metallic materials in automotive applications. Metals. 2020;10(4):434.
5. Ptačinová J, Dománková M, Hudáková M, et al. Identification of carbides in sub–zero treated vanadis 6 ledeburitic steel. Key Engineering Materials. 2015;647:9–16.
6. Kobayashi S, Takasugi T. Mapping of 475 degrees C embrittlement in ferritic Fe–Cr–Al alloys. Scripta Mater. 2010;63:1104–1107.
7. Maugis P, Chentouf S, Connétable D. Stress–controlled carbon diffusion channeling in bct–iron: A mean–field theory. Journal of Alloys and Compounds. 2018;769:1121–1131.
8. Tasan C, Diehl M, Raabe D. Modeling of materials: development with simulation–discoveries through simulation. Multiscale materials simulation. Winter school, German Research Foundation SPP Aachen Germany; 2017.
9. Tapasa K, Barasheva AV, Bacona DJ, et al. Osetsky. Computer simulation of carbon diffusion and vacancy– carbon interaction in α–iron. Acta Materialia. 2007;55(1):1–11.
10. Fu CC, Meslin E, Barbu A, et al. Effect of C on vacancy migration in α–iron. Solid State Phenomena. 2008;139:157–164.
11. Mukherjee D, Larsson H, Odqvist J. Phase–field modeling of diffusion induced grain boundary migration in binary alloys. Computational Material Science. 2020;184:1–9.
12. Zhou P, Ma QX. Determination of recrystallization kinetics model of 30Cr2Ni4MoV steel based on dislocation density. Solid State Phenomena. 2017;263:59–66.
13. Schneider A, Fu CC, Soisson F, et al. Atomic diffusion in α–iron across the curie point: an efficient and transferable Ab initio–based modeling approach. Phys Rev Lett. 2020;124:215901.
14. Ferrari A, Dutta B, Gubaev K, et al. Frontiers in atomistic simulations of high entropy alloys. Journal of Applied Physics. 2020;128(15):0025310.
15. Glensk A, Grabowski B, Hickel T, et al. Breakdown of the Arrhenius law in describing vacancy formation energies: the importance of local anharmonicity revealed by Ab initio thermodynamics. Physical Review. 2014;X4(1):011018.
16. Haman KJ. Diffusion carbon in α–iron/Diffusion in body–centered cubic metals [in Russian]. Metallurgy M. 1978. 83 p.
17. Ya I Frenkel. Introduction to the Theory of Metals [in Russian]. Fizmathiz, 1948.
18. Bokshtein BS, Diffusion in metals [in Russian]. Metallurgy M. 1978. 248 p.
19. Kimizuka H, Mori H, Ogata S. Effect of temperature on fast hydrogen diffusion in iron: A path–integral quantum dynamics approach. Phys Rev B: Condens Mater Phys. 2011;83:094110.
20. Fujii H, Tsurekawa S. Diffusion of carbon in iron under magnetic fields. Phys Rev B. 2011;83:054412.
21. Lifshits EM, Pitaevskiy LP. Statistical physics. Part 2. Theory of condensed matter [in Russian]. Fizmatlit; 2000. 496 p.
22. Kozheurov VA. Statistical thermodynamics [in Russian]. Metallurgy M. 1975. 175 p.
23. Bobyr SV. Statistical model of impurity atoms diffusion in the crystal lattice of metals and its application for calculating the diffusion coefficients of hydrogen and carbon atoms in iron. Phys Solid State. 2021;3:345.
24. Bobyr SV. Theoretical aspects of hydrogen diffusion in metals. Scientific Herald of Uzhhorod University Series “Physics”. 2021;50:31–38.
25. Larikov LN, Isaychev VI. Diffusion in metals and alloys, Kiev, Naukova dumka. 1987. 510 p.
26. Bobyr SV, Krot PV, Loschkarev DV. Models of structural phase transformations and mechanical properties of alloy steels rolls. Chapter in book Carbon Steel: Microstructure, Mechanical Properties and Applications. Hauppauge (USA), Nova Science Publishers, Inc; 2019:81–106. ISBN 978–1–53615–436–8.
27. Covenskiy II. Study carbon diffusion in three refractory metals over a wide temperature range/Diffusion in body–centered cubic metals [in Russian]. М Metallurgy; 1978. 284 p.