Carbon diffusion in metals has received a lot of attention and has been the subject of intensive theoretical investigations in recent years. The purpose of this work is development the statistical calculation model (SCM) on the diffusion of carbon in metals and its application for calculating the diffusion coefficients of carbon in alloys. It includes first-principles calculation of the diffusion coefficient according to a statistical model, physicochemical calculation of activation energies for carbon, and linear approximation of carbon diffusion in alloys. The calculated values of the diffusion coefficient for metals are within the range of the experimental values. For low-melting metals, carbon diffusion coefficients are mainly unknown from experiment, but the statistical model allows us to predict their values. The calculations are compared with known experimental data on the diffusion of carbon atoms in some metals Fe, V, Ta and W at high temperatures with fairly good agreement between the results. The SCM-model allows us to determine the influence of the alloying elements Si, Mo and Cr on the diffusion of carbon in the F – C alloy.

Keywords: metals, statistical model, carbon diffusion, activity, diffusion coefficient, activation energy, alloys

Alloys of the Fe-C system with alloying elements remain the most important for technological applications in the automotive industry.^1,2 High strength steels containing significant fractions of retained austenite have been developed in recent years.² In sheet steels carbon-enriched metastable retained austenite is considered beneficial because the TRIP phenomenon during deformation can contribute to formability and energy absorption.³

The processes of thermal strengthening of such steels and alloys are determined, first of all, by the possibility of their phase-structural transformations.^4,5 In steels and cast irons, the kinetics of transformation of austenite largely determined by the diffusion of carbon, which allows them to refer to transformations controlled by diffusion.^4,5

Eutectoid transformation of austenite, as a kind of diffusion transformation, associated with a sharp change in the composition of the phases and the formation of colonies or aggregates of the two phases in the process of carbon diffusion from austenite to cementite.⁵ The processes of carbide formation and carbide transformation in steels and alloys are also determined by the diffusion of carbon between the phases.⁶ Diffusion of interstitial carbon atoms in iron is the rate-limiting phenomenon of a number of phase transitions in body-centered (bсc) and body-centered tetragonal (bct) phases such as ferrite and martensite.⁷

It is therefore important to correctly determine and calculate the diffusion coefficients of carbon in metals and alloys at different temperatures, taking into account the influence of alloying elements.

To quantify the effect of diffusion elements on phase transformation, multi-scale modeling is required.⁸ The numerical tools that are applied include phase-field modeling and quasicontinuum rate theory, fitting of effective many-body interaction potentials, molecular dynamics simulation, Monte Carlo simulation of defect evolution and ab initio DFT-calculations.^7–16 These methods are often very complex and have their limits of their applicability for modeling steels and alloys.¹⁶

In iron crystals, carbon atoms are in interstitials and in the diffusion process they pass from one interstitial site to another. In FCC lattice, carbon can occupy octahedral type of interstitial sites⁷ but also diffuse through the tetrahedral type of interstitial sites. At the present time, the question of the carbon diffusion mechanism in the crystal lattice of iron remains. Even in a pure crystal, transitions between interstitials of different types are possible, which entails, in particular, the ambiguity of the activation energy of carbons diffusion. In addition, as noted in,⁷ the redistribution of carbons atoms in interstitial sites due to changes in external conditions, for example, deformation, can lead to a change in the diffusion parameters. It should be noted that other factors may also lead to deviations from the Arrhenius law, in particular, the possibility of diffusion jumps of different lengths and the effect of crystal lattice defects.^12,17

First principles calculations and classical approaches molecular mechanics has been used to study carbon diffusion in the case of body-centered cubic (BCC) Fe in several papers.^{7,12,15,18,19}

In²⁰ the statistical model for calculating the carbon diffusion parameters in iron and steel was presented. Unfortunately, this model used experimental values ​​of diffusion coefficients to determine the diffusion parameters of the statistical model. It is of undoubted interest to develop such a model for determining the pre-exponential factor from first principles and to generalize it for calculating the carbon diffusion coefficients in other metals and alloys.

The purpose of this work is development the statistical calculation model on the diffusion of carbon in metals and its application for calculating the diffusion carbon coefficients in alloys.

Calculation of diffusion coefficient

In the classical limit and using the random-walk model of interstitial diffusion in a BCC lattice $D_{\text{0}}$ , in the Arrhenius expression for the diffusion parameter $D=D_{\text{0}}exp(-E_a/RT)$ can be represented as¹⁹:

$D_{\text{0}}=\frac{n{\Delta }^{\text{2}}}{\text{6}}\frac{{\prod }_{j=\text{1}}^{\text{3}N}{\nu }_j}{{\prod }_{j=\text{1}}^{\text{3}N}{\nu }_j^{+}}$   (1)

where,n is a geometrical factor for the number of equivalent jump paths,$\Delta$ is the jump length, and ${\nu }_j$ and ${\nu }_j^{+}$ are the real normal mode frequencies at the initial state and the transition state, respectively.

In²¹ it is proposed to use statistical model expressions for the pre-exponential coefficient. This approach, based on the principles of statistical thermodynamics, makes it possible to adequately consider the statistical distribution of impurity atoms according to their energy.

$I_i=-\frac{\text{2}\pi C_i{m}_i{k}^{\text{2}}{T}^{\text{2}}d}{N{h}^{\text{3}}}{e}^{-\frac{u-{\mu }_0}{kT}}{\gamma }_i\frac{\partial c_i}{\partial х}\text{.}$   (2)

(in equation (2) it is assumed that the activity coefficient ${\gamma }_i$ does not depend on the x coordinate).

When the pre-exponential factor in our case is:

$D_{\text{0}}^i=\frac{\text{2}\pi C_i{m}_i{\gamma }_i{k}^{\text{2}}{T}^{\text{2}}d}{N{h}^{\text{3}}}$   (3)

We see that the diffusion coefficient depends at three points (k, N and h), in two parameters ( $m_i$ is the mass of the i-diffusive atom and d is the interplanar distance), the amount of substance in the volume $C_i$ , their activity coefficient ${\gamma }_i$ and temperature of the metal in square.

We write the mass of atoms of the diffusing element in the form of the expression:

$m_i=N_i·m_a,$   (4)

where $N_i$  is the atomic number of the element; $m_a$ is the atomic mass unit.

We also take into account that c is related to the concentration of $C_i$ by the expression:

$C_i=c_i·M_i/\rho ,$   (5)

where $\rho$ is the alloy density (g · сm^-3).

where $M_i$  is the atomic massa of the element $(g·mo{l}^{-\text{1}})$ ; in this units $M_i=N_i;$

$c_i$  is the number of moles of the diffusing element per unit volume $(mol·s{m}^{-\text{3}}).$

Then the expression for the diffusion coefficient of the atoms of the dissolved element in the metal takes the form:

$D_{\text{0}}^i=\frac{\text{2}\pi m_a{k}^{\text{2}}d}{h^{\text{3}}N\rho }\cdot A_i\cdot N_i^{\text{2}}\cdot T^{\text{2}},$   (6)

where $A_i={\gamma }_i·c_i$ - activity element i in solid solution. The activity of this element is generally unknown and this parameter is need to be determined from experimental data on diffusion or performed calculations.

Expression (6) of the developed statistical model significantly differs from the expressions obtained in classical atomic models.^18,19 The interplanar distance  enters into this expression in the first degree. Nevertheless, this formula assumes the dependence of $D_{\text{0}}$ on the square of the atomic number of the diffusing element and the square of the diffusion temperature.

For comparative calculations, we assumed the following model parameters:

d = a, a is the parameter of the crystal lattice of the metal - solvent,

${\gamma }_i=\text{1},c_i=\text{0}\text{.01}\left(\text{1 }at.\%C\right),A_i=\text{ 0}\text{.01},N_i=\text{12 }forC$ , and formula (6) for carbon diffusion coefficient in metal has the form:

$D_{\text{0}}=\text{0}\text{.164}\frac{a}{\rho }\cdot T^{\text{2}}$   (7)

The parameters, calculated in this way, can be called the parameters of the statistical calculation model (SCM).²¹ The classical expressions for calculating diffusion coefficients does not take into account the Boltzmann distribution of diffusing particles in energy.

Calculation of diffusion energy activation and coefficient of carbon in alloys

To calculate the diffusion coefficients of carbon in metals, many diffusion equations are known, constructed from experimental data.^22–28 These experimental data will be used to construct the distribution of experimental values of diffusion coefficients and activation energies of carbon diffusion in metals together with calculated values.

The activation energies of carbon in metals, primarily in iron, are calculated from first principles using DFT calculations^{7,11,18,29,30} and included in the calculation model database. However, these calculations are highly accurate at low temperatures and may be inaccurate at diffusion temperatures close to the melting point of the metal. There are also reliable experimental data for the diffusion of carbon in ²² which are used as verification data for our calculations.

So, reliable experimental or calculated data are known only for a small number of metals.^22–25 Therefore, to estimate the activation energy of carbon diffusion in metals, physicochemical methods for establishing correlations should be used.

From books on diffusion in metals, the correlation between the activation energy of self-diffusion in metals and the heat and melting point of the metal is well known.^26,27 It is also known that the activation energy of carbon in metals is approximately three times less than the activation energy of self-diffusion. Therefore, for metals for which the activation energy is still unknown, we use the correlation relationship between the activation energy of carbon diffusion and the melting temperature of the $\text{i-element}{T}^{i}melt:$

$E^i{}_a=K_{\text{0}}k{T}^{i}melt,$    (8)

k is the Boltzmann constant,

$K_{\text{0}}$ is a constant coefficient (~ 5.5 for C diffusion).

The $K_{\text{0}}$ coefficient was selected from the correspondence of the activation energy calculated using formula (8) with reliable data from theoretical work²⁹ and experimental work²² on the diffusion of carbon in $\text{α-iron}\text{.}$

For practical calculations of multicomponent systems - alloys in the developed statistical calculation model (SCM) the diffusion coefficient D and the activation energy of carbon diffusion we can calculate by the theme formulas (7) and (8) with the corresponding alloy density parameters ρ, averaged parameter crystal lattice a and melting point of the alloy.

When these parameters are unknown, and it is in this case that a calculation model is used, the carbon diffusion coefficient D_C in the alloy was calculated using the linearized formula:

$D_C={\displaystyle \sum }_{i=\text{1}}^N C_i{D}_i,$   (9)

where N is the number of elements in the alloy,

$C_i$  is i-element concentration in alloy and

$Di=D^i{}_{\text{0}}\exp \left(-E^i{}_a/kT\right),$   (10)

is the partial diffusion coefficient carbon in element i.

The statistical calculation model for metals and alloys was implemented in the corresponding database, including 43 base metals and silicon, and created software.

A comparison of experimental and calculated data on the values of the diffusion parameters for metals

A comparison of experimental and calculated data on the values of the diffusion coefficient for metals is shown in Figure 1. The calculated values of were performed according to formula (7).

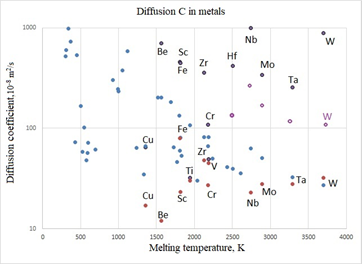
Figure 1 Comparison of experimental and calculated data on the values of the diffusion coefficient for metals, blue circles show calculated values of $D^i{}_{\text{0}}$ according to formula (7) with T = 1000K, purple circles are lower experimental values, dark gray circles are upper experimental values, transparent purple circles represent calculated $D^i{}_{\text{0}}$ values according to formula (7) with T=2000 K for refractory metals.

Figure 1 shows that the calculated values of the Diffusion coefficient for metals are within the range of the experimental values. For refractory metals, the calculated values of the diffusion coefficient at T = 2000 K are in better agreement with the experimental values, which can be explained by the fact that carbon diffusion measurements for these metals were carried out at higher temperatures.

For low-melting metals, carbon diffusion coefficients are mainly unknown from experiment. A statistical model allows one to predict their values.

In Figure 2 shows experimental and calculated data on the values of the activation еnergy for metals.

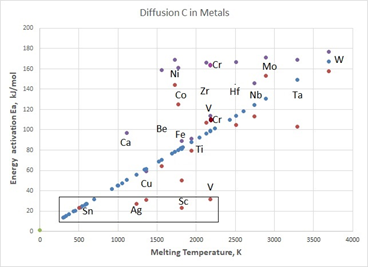
Figure 2 Comparison of experimental and calculated data on the values of the Energy activation for metals, blue circles show calculated values of $E^i{}_a$ according to formula (8), purple circles are lower experimental values, dark gray circles are upper experimental values.

Calculated data on the values of the energy activation for metals fall on a straight line relative to the melting point. The experimental values are scattered around this line, especially for the first group of elements, such as Be, Fe, Ti, Hf, Nb, Ta, W.

Two another groups of metals should be distinguished. One group of metals with a high melting point Ni, Co, Zr, Cr and Mo has experimental activation energies for carbon diffusion that are greater than the calculated ones. These metals should be used to make alloys that are stable at high operating temperatures.

Another group of metals is highlighted in the figure by a rectangle Sn, Ag, Cu, Sc and V have low experimental values of activation energy for carbon diffusion. This may indicate the possibility of quantum diffusion of carbon at low temperatures in these metals, as well as other metals with low melting points located in the rectangle. Quantum diffusion in such elements can be taken into account by corresponding DFT – calculations of the activation energy of carbon diffusion in such metals at low temperatures.

A comparison of experimental and calculated data on the values of diffusion coefficients for some selected metals

In this section, a comparison is made of the SCM-calculated data and the experimental data of the diffusion coefficients obtained earlier in the corresponding works and represented by the Arrhenius equation. The values of the carbon diffusion coefficients in iron and vanadium are shown in Figure 3 and 4 respectively.

From Figure 3 and 4 one can see a fairly good agreement between the values calculated using the Arrhenius equation and the SCM model. The SCM model is quite efficient for estimating carbon diffusion coefficients in metals with an average melting point.

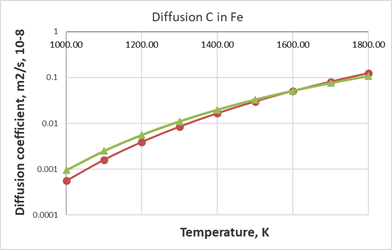
Figure 3 Comparison of calculated data on diffusion coefficient values for C in Fe, red circles show calculated values from the SCM $(Ea=\text{ 0}\text{.86 }eV),$ green triangles represent values from Arrhenius equation with $D_{\text{0}}=\text{ 39}\text{.4}\times {\text{10}}^{-\text{8}}{m}^{\text{2}}/sandEa=\text{ 0}\text{.96 }eV$ from.²⁴

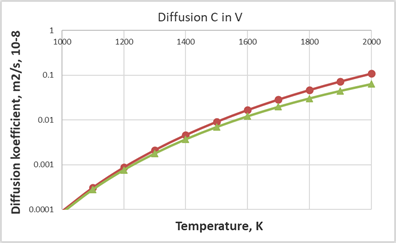
Figure 4 Comparison of calculated data on diffusion coefficient values for for C in V, red circles show calculated values from the SCM $(Ea=\text{ 1}\text{.03 }eV),$ green triangles represent values from Arrhenius equation with $D_{\text{0}}=\text{ 49}\text{.0}\times {\text{10}}^{-\text{8}}{m}^{\text{2}}/sandEa=\text{ 1}\text{.2 }eV$ from.²⁷

Similar calculations were performed for two refractory metals - Ta and W. In this case, experimental data from two different sources were taken into account. Comparison of calculated data on diffusion coefficient values for C in Ta and W represents on the Figure 5 and 6 respectively.

From these figures it is clear that the SCM model fits well at least one experimentally obtained Arrhenius equation.²⁸ For Ta, almost complete agreement with the experimental results of the another work²³ is observed in the high-temperature region (Figure 5).

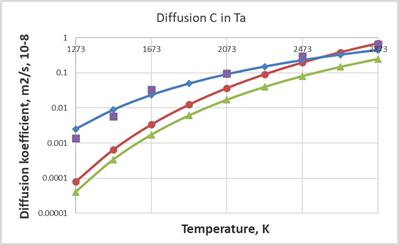
Figure 5 Comparison of calculated data on diffusion coefficient values for C in Ta, red circles show calculated values from the SCM $(Ea=\text{ 1}\text{.75 }eV)$ , green triangles represent values from Arrhenius equation with $D_{\text{0}}=\text{ 2}\text{.57}\times {\text{10}}^{-\text{6}}{m}^{\text{2}}/sandEa=\text{ 1}\text{.8 }eV,$ ²⁸ blue rombes and purple squares represent calculated values with $D_{\text{0}}=\text{ 27}\text{.8}\times {\text{10}}^{-\text{8}}{m}^{\text{2}}/sandEa=\text{ 1}\text{.07 }eV$ and experimental values from ²³ respectively.

For W, agreement between the experimental results of the work²⁸ and the SCM points is observed in the region of lower temperatures (Figure 6). However, taking into account the phenomenological nature of the activation energy values in the SCM model, such a correspondence is quite favorable and indicates the efficiency of this model in physicochemical calculations of diffusion processes in metals.

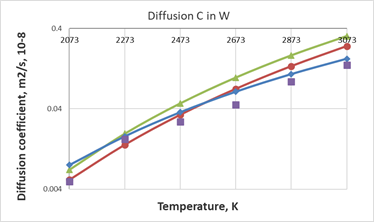
Figure 6 Comparison of calculated data on diffusion coefficient values for W, red circles show calculated values from the SCM $(Ea=\text{ 1}\text{.75 }eV),$ green triangles represent values from Arrhenius equation with $D_{\text{0}}=\text{ 8}\text{.91}\times {\text{10}}^{-\text{6}}{m}^{\text{2}}/sandEa=\text{ 2}\text{.2 }eV$ from,²⁸ blue rombes and violet squares represent calculated values with $D_{\text{0}}=\text{ 92}\text{.2}\times {\text{10}}^{-\text{8}}{m}^{\text{2}}/sandEa=\text{ 1}\text{.75 }eV$ and experimental values from ²³ respectively.

To increase the accuracy of calculations in the SCM model, it is necessary to take into account the values of the activation energy of diffusion, calculated from first principles, taking into account their dependence on temperature.^29–35 However, in this case, the SCM model ceases to be predictive for other metals.

Calculated data on the values of the diffusion coefficients for alloys Fe – C – Alloying element

To assess the performance of the proposed SCM model in alloys, the values of the diffusion coefficients for alloys Fe – C – Si, Fe – C – Mo, Fe – C – Cr using formula (9) were calculated. In addition to metals, the elemental data base also included silicon, as an important alloying element for many alloys. Calculated data from the SCM on diffusion coefficient for C in alloys Fe – C – Alloying element at 1000 K represent on the Figure 7.

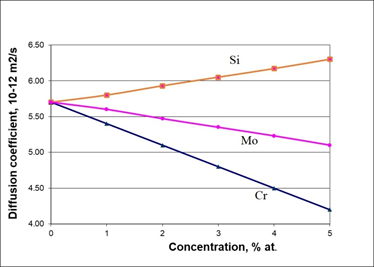
Figure 7 Calculated data from the SCM on diffusion coefficient for C in alloys Fe – C – Alloying element at 1000 K, orang squares represent Si, rose circles show Mo and blue triangles represent Cr.

Figure 7 shows that, according to the SCM-model, silicon increases the diffusion coefficient C in iron, while Mo and Cr, on the contrary, reduce it. These results are in good agreement with well-tested experimental physicochemical models.^36,37 According to them, Si increases the activity of carbon in Fe – C alloys, while Mo and Cr decrease it, reducing the diffusion of C.

At the same time, in,³⁰ after laborious DFT calculations, it was found that silicon reduces the diffusion of carbon in the Fe – C alloy, which contradicts the physicochemical models.^36,37

Consequently, to estimate the values of the carbon diffusion coefficient in alloys, a simple SCM model represented by the linear equation (9) can be used.

To increase the accuracy of SCM model calculations, instead of equation (9), one should use both more accurate physicochemical models of carbon activity in alloys³⁶ and methods for finding the diffusion activation energy values from first principles,^29–35 taking into account its dependence on temperature.

For practical calculations of carbon diffusion in multicomponent systems - alloys statistical calculation model (SCM) has been developed. It includes first-principles calculation of the diffusion coefficient according to a statistical model, physicochemical or first-principles calculation of activation energies for elements (metals and Si), and linear approximation of carbon diffusion in alloys.The statistical calculation model for metals and alloys was implemented in the corresponding database, including 43 base metals and Si, and created software.

The calculated values of the diffusion coefficient for metals are within the range of the experimental values. For refractory metals, the calculated values of the diffusion coefficient at T = 2000 K are in better agreement with the experimental values. For low-melting metals, carbon diffusion coefficients are mainly unknown from experiment, but the statistical model allows us to predict their values.

Calculated data on the values of the energy activation for metals fall on a straight line relative to the melting point according to the used physicochemical model. The experimental values are scattered around this line, especially for the first group of elements, such as Be, Fe, Ti, Hf, Nb, Ta, W. Second group of metals with a high melting point Ni, Co, Zr, Cr and Mo has experimental activation energies for carbon diffusion that are greater than the calculated ones. These metals should be used to make alloys that are stable at high operating temperatures.

Another group of metals includes Sn, Ag, Cu, Sc and V, it have low experimental values of activation energy for carbon diffusion. This may indicate the possibility of quantum diffusion of carbon at low temperatures in these metals, as well as other metals with low melting points located in the rectangle. Quantum diffusion in such elements can be taken into account by corresponding DFT – calculations of the activation energy of carbon diffusion in such metals at low temperatures.

The calculations are compared with known experimental data on the diffusion of carbon atoms in some metals Fe, V, Ta and W at high temperatures with fairly good agreement between the results.

The performance of the proposed SCM model in the alloys Fe – C – Alloying element has been assessed. The SCM-model allows us to determine the influence of the alloying elements Si, Mo and Cr on the diffusion of carbon in the F – C alloy, which has important practical application.

Unfortunately, this linear model does not allow us to take into account all the factors of the mutual influence of elements on the diffusion coefficients of carbon in alloys and activation energy. Further development of this model will allow us to consider the influence of these factors on the diffusion of carbon in iron and alloys.

This project was funded by the Swedish Foundation for Strategic Research (SSF), contract UKR24-0017. We acknowledge prof. Martin Sahlberg from Uppsala University for support.

None.

The authors declare that there is no conflict of interest.

1. Ramazani A, Berme B, Prahl U. Structural materials and processes in transportation. First Edition. Wiley-VCH Verlag GmbH & Co. KgaA. 2013;5–47.
2. Chatterjee D. Behind the development of advanced high strength steel (AHSS) including stainless steel for automotive and structural applications - an overview. Material Sci Metal Eng. 2017;4(1):1–15.
3. Speer JG, Assunção FCR, Matlocka DK, et al. The “quenching and partitioning” process: background and recent progress. Mat Res. 2005;8(4):417–423.
4. Totten GE. Steel heat treatment. Metallurgy and technologies. Second edition.  Portland: Taylor & Francis Group LLC. 2006;810.
5. Bobyr SV. Using the principles of nonequilibrium thermodynamics for the analysis of phase transformations in iron-carbon alloys. Chapter in the book Non-Equilibirum Particle Dynamics, London: Intechopen. 2019;134.
6. Bobyr S, Odqvist J. Diffusion kinetics in a multicomponent thermodynamic system at small deviations from the equilibrium state. Phys Chem Solid State. 2024;25(2):406–412.
7. Zhang X, Hickel T, Rogal J, et al. Structural transformations among austenite, ferrite and cementite in Fe–C alloys: A unified theory based on ab initio simulations. Acta Materialia. 2015;99:281–289.
8. Tasan C, Diehl M, Raabe D. Modeling of materials: development with simulation –discoveries through simulation. Multiscale materials simulation. Winter school, German Research Foundation SPP Aachen Germany. 2017.
9. Hoglund L, Agren J. Simulation of carbon diffusion in steel driven by a temperature gradient. J Phase Equilibria Diffusion. 2010;31(3):212–215.
10. Maugis P, Chentouf S, Connétable D. Stress-controlled carbon diffusion channeling in bct-iron: A mean-field theory. J Alloys Compounds. 2018;769:1121–1131.
11. Tapasa K, Barasheva AV, Bacona DJ, et al. Computer simulation of carbon diffusion and vacancy- carbon interaction in α-iron. Acta Materialia. 2007;55(1):1–11.  
12. Fu CC, Meslin E, Barbu A, at al. Effect of C on vacancy migration in α-iron. Solid State Phenomena. 2008;139:157–164.
13. Mukherjee D, Larsson H, Odqvist J. Phase-field modeling of diffusion induced grain boundary migration in binary alloys. Computational Mat Sci. 2020;184:109914.
14. Zhou P, Ma QX. Determination of recrystallization kinetics model of 30Cr2Ni4MoV steel based on dislocation density. Solid State Phenomena. 2017;263:59–66.
15. Schneider A, Fu CC, Soisson F, et al. Atomic diffusion in α-iron across the curie point: an efficient and transferable Ab Initio–based modeling approach. Phys Rev Lett. 2020;124:215901.
16. Ferrari A, Dutta B, Gubaev K, et al. Frontiers in atomistic simulations of high entropy alloys. J Appl Phys. 2020;128(15):0025310.
17. Glensk A, Grabowski B, Hickel T, et al. Breakdown of the Arrhenius law in describing vacancy formation energies: the importance of local anharmonicity revealed by Ab initio thermodynamics. Phys Rev. 2014,4(1):011018.
18. Fujii H, Tsurekawa S. Diffusion of carbon in iron under magnetic fields. Phys Rev B. 2011;83(5):054412.
19. Jiang DE, Carter EA. Diffusion of interstitial hydrogen into and through bсc Fe from first principles. Phys Rev B. 2004;70(6):064102.
20. Bobyr SV. Statistical model of impurity atoms diffusion in the crystal lattice of metals and its application for calculating the diffusion coefficients of hydrogen and carbon atoms in iron. Phys Solid State. 2021;63:420–424.
21. Bobyr SV, Loschkarev DV, Sharfnadel SA. Development of a statistical model calculating the carbon diffusion parameters in steels. Material Sci & Eng. 2022;6(4):146–150.
22. Homan KJ. Diffusion of carbon in α-iron. Diffusion in metals with a body-centered lattice [in Russian]. Ed. S. Z. Bokshtein. Metallurgy, Moscow. 1969.
23. Covenskiy II. Study carbon diffusion in three refractory metals over a wide temperature range / diffusion in body-centered cubic metals [in Russian]. Metallurgy М. 1978.
24. Larikov LN, Isachev VI. Diffusion in metals and alloys/ structure and properties of metals and alloys. Directory [in Russian]. Naukova Dumka, Kyiv. 1987.
25. Restrepo OA, Becquart CS, El-Mellouhi F, et al. Diffusion mechanisms of C in 100, 110 and 111 Fe surfaces studied using kinetic activation-relaxation technique. Acta Materialia. 2017;136:303–314.
26. Bokshtein BS. Diffusion in metals [in Russian]. Metallurgy М. 1978.
27. Fedorov GV, Smirnov EA. Diffusion in reactor materials [in Russian]. Atomizdat M. 1978.
28. Nikonechnikov AI, Pavlinov LV, Bykov VN. Carbon diffusion in refractory metals with a bcc lattice [in Russian]. FMM. 1966;22(2):234.
29. Jiang DE, Carter EA. Carbon dissolution and diffusion in ferrite and austenite from first principle. Phys Rev B. 2003;67(21):214103.
30. Simonovic D, Ande CK, Duff AI, et al. Diffusion of carbon in bcc Fe in the presence of Si. Phys Rev B. 2010;81(5):054116.
31. Schenter GK, Mills G, Jonsson H. Reversible work-based quantum transition state theory. J Chem Phys. 1994;101(10):8964–8971.
32. Marx D, Parrinello M. Ab initio path integral molecular dynamics: Basic ideas. J Chem Phys. 1996;104(11):4077–4082.
33. Richardson JO, Althorpe SC. Ring-polymer molecular dynamics rate-theory in the deep-tunneling regime: Connection with semiclassical instanton theory. J Chem Phys. 2009;131(21):214106.
34. Kimizuka H, Mori H, Ogata S. Effect of temperature on fast hydrogen diffusion in iron: a path-integral quantum dynamics approach. Phys Rev B. 2011;83(9):094110.
35. Kwon H, Shiga M, Kimizuka H, et al. Accurate description of hydrogen diffusivity in bcc metals using machine-learning moment tensor potentials and path-integral methods. Acta Materialia. 2023;247:118739.
36. Silman GI. Thermodynamics and thermokinetics of structure formation in cast irons and steels. Mechanical Engineering, M. 2007.
37. Bobyr SV, Krot PV. Nonequilibrium thermodynamic analysis of diffusion processes in the steel - carbon thin film tribological system. Material Sci & Eng. 2022;6(1)14–18.