Faulting, a critical distress in rigid pavements, poses a crucial challenge to road safety and maintenance. It is defined as the elevation difference of transverse joints in Jointed Plain Concrete Pavements, which is primarily caused due to environmental effects, subgrade properties, and accumulated traffic loads. Traditional regression models cannot often capture complex relations within pavement faulting and other detrimental effects on pavement, whereas Artificial Neural networks leverage data-driven machine-learning approaches to provide more accurate predictions. Datasets have been prepared from the LTPP database of dry climate zones. Environmental factors such as Yearly ESALs, Annual Precipitation, Annual Average Temperature, Freeze-Thaw Cycles, and structural properties like Pavement Thickness, Pavement Age, Tensile Strength, and Optimum Moisture Content (OMC) are considered the factors causing wheel path faulting. An Artificial Neural Network (ANN) based faulting prediction model is developed with one hidden layer and three neurons. 8 States over 30 years of lifespan are taken into consideration for this study. The final developed ANN model can predict the faulting in pavement sections accurately for any climatic region with an R2 value of 0.81. The correlation between the factors is studied as well and an ANN linear equation is also developed. The developed predictive ANN model equation will allow transportation engineers and contractors to easily predict Faulting in Jointed Plain Concrete Pavements (JPCP) which will assist in improving maintenance strategies to alleviate the effects of JPCP faulting.

Jointed Plain Concrete Pavement (JPCP) is one of the most common types of rigid pavements that consist of concrete slabs with steel mesh reinforcement. Faulting, a critical distress occurs in JPCP when transverse joints of adjacent slabs differ in elevation. Several factors such as heavy traffic load, soil stripping in the base layer, moisture infiltration at joints, differential settlement, and temperature variation in the slab may cause faulting.

Faulting is a major issue in jointed concrete pavements (JCPs). Many prediction models are being developed for predicting fault failure. In AASHTO 1993 version of pavement design guide, faulting and cracking were combinedly accounted for by maintaining and serviceability above defined threshold. In the attempted to separate these two concerns and forecast faults independently based on pavement design, traffic, weather conditions.¹ Most of the prediction models used LTPP database in which Faulting data include faulting measurements at doweled and non-doweled joints and some measurements at transverse crack locations. Ehsani et al.² used both artificial neural and random forest method with 19 input variables to develop prediction model. Ker et al.³ developed prediction model for transverse joint faulting incorporating ERESBACK 2.2 program for back calculation to get more accurate data. Mechanistic-empirical erosion-based faulting model incorporated traffic parameters with the application of erosion test showed the correlation between traffic , environmental factors with faulting.⁴ Darter et al.⁵ incorporated Monte Carlo Simulation into the M-E PDG JPCP cracking prediction in which pavement layer thickness, joint spacing, co-efficient of subgrade reaction, tire pressure etc. were studied. The current faulting model integrated into the Pavement ME design procedure considers pavement response, climatic conditions, traffic, and base erodibility.⁶ This model is uniformly applied to all types of jointed concrete pavements, regardless of their structural makeup (such as conventional concrete pavement, unbonded concrete overlay, bonded concrete overlay, etc.). This suggests that the pumping mechanism is assumed to be consistent across all pavement structures. Furthermore, it assumes uniformity in the rate of faulting development and the maximum faulting regardless of pavement structure. The focus of this study is to build an ANN model capable of predicting faulting for dry region by incorporating both structural and environmental variables of JPCP.

The main objective of the study is to utilize a machine-learning approach principally an ANN base model for future faulting prediction in JPCP. The model is trained by datasets collected from LTPP for the dry climatic zone in the US. Both structural properties and environmental effects are considered for neural net development thus creating a well-grounded prediction model. The study also derives a first-degree simplified equation from the ANN model, which can be utilized by pavement engineers and maintenance contractors to predict future faulting development in JPCP. The sensitivity analysis of the model input parameters is performed to investigate the inner connectivity between input parameters and output results.

For training the neural network model data sets are collected from The LTPP database. The LTPP program regularly collects joint and crack faulting data at each jointed concrete pavement test site using the Georgia Fault Meter (GFM). Figure 1 shows the diagram for GFM faulting measurement. The faulting measurements over 30 years of lifespan at the wheel path for the Dry-Freeze and Dry No-Freeze climate regions subjected to this study are shown in Figure 2 & 3. A total of 190 observations in 8 states are fed into the ANN model for both front and back training propagation. Linear regression shows the existing correlation between which was further evaluated by correlation heatmap presented in Figure 4. ESAL and pavement thickness demonstrate the highest positive correlation, reaching 0.5. Conversely, the annual average temperature exhibits a significant negative correlation (-0.74) with faulting formation, indicating a strong inverse relationship between the two variables.

Figure 1 Diagram of manual faulting measurement using the GFM. (Source: FHWA)

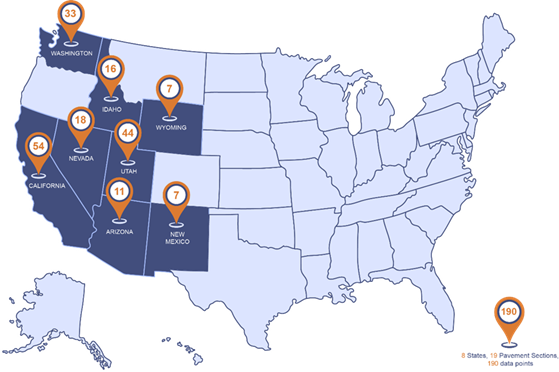
Figure 2 Study area containing states with observations numbers in dry climatic region. The database included four structural and four environmental factors which are shown in Figure 3.

Figure 3 Input variables for ANN model training. The training dataset of the neural network is initially evaluated with linear regression analysis and R² is observed to be 0.269, represented in Table 1. This accuracy was enhanced through the machine learning approach.

Figure 4 Correlation heatmap between input parameters and output parameters.

The ANN model requires the datasets to be standardized for training. Table 2 represents the maximum, minimum, average, and standard deviation of the training dataset. These values are used further for equation development process. A multilayer perceptron (MLP) based ANN consists of fully inner connected neurons which have three types of layers, input layer, hidden layers, and output layer. The input layer receives the input data sets which are processed through one or more hidden layers using mathematical operations. Finally, the model’s prediction is produced by output layer based adjusted weights and biases. The algorithm gradually corrects the weights among the different units and for this, the algorithm evaluates the difference between the output predictions produced by the MLP and the actual desired values. This learning method is feedforward backpropagation.⁷ For this study the dataset is initially normalized. Normalization is a process to change the dataset into a specific range. It is necessary where the input features has big differences in ranges.⁸ For faulting prediction ANN, min-max normalization is used to rescale the input variables range between -1 to +1, shown in Equation 1. With this method, the relational properties in data remains the same, changing the range only.⁹

$\text{X}=2\times \frac{\text{X}-\text{Xmin}}{\text{Xmax}-\text{Xmin}}$  (1)

Where,

X = Normalized Value of the parameter x

X_min = Minimum value of the parameter x

X_max = Maximum Value of the parameter x

To tackle the zero-gradient problem in Tanh, a scaled Hyperbolic Tangent is used¹⁰ which is defined as, Hyperbolic Tanh(x) = A × Tanh(B × x)  with output range in [−A, A].

For training the MLP three hidden neurons are used with 8 input neurons and one output neuron. Figure 5 shows the ANN architecture for the model. The MLP Model Output can be described as the following Equation 2,

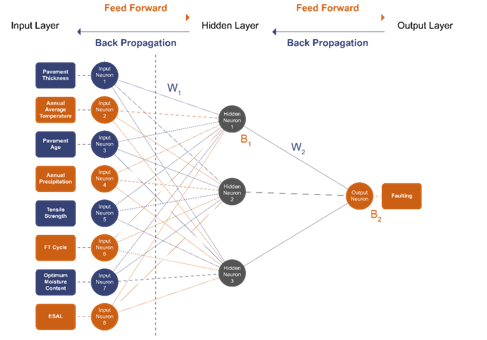
Figure 5 Architecture of an ANN-based model with 8 input variables with 3 neurons in 1 hidden layer.

Output$=\left({\omega }_1\text{}{x}_1\text{}+{\omega }_2\text{}{x}_2\text{}+\dots +{\omega }_{n\text{}}{x}_n\text{}+\beta \right)$    (2)

Where,

𝑓 = activation function applied to the weighted sum of inputs plus a bias term

ω₁, ω₂,…, ω_n​ = Weights associated with each input

x₁, x₁,…, x_n​ = Input values

β = bias term

The dataset of total 190 observation were randomly split into three subgroups, 70% dataset is used for training the ANN model, 15% for validating of the model and 15% for testing the prediction outcomes. This division is done to avoid overfitting the model and create the model more reliable. While training the model the loss function The Root Mean Squared Error (RMSE) is observed on validation datasets. If the loss value on validation data sets did not reduce up to six times, the training would stop. For training the MLP, The Levenberg-Marquardt Algorithm is used as it performs greatly than simple gradient descent and other conjugate gradient optimization.¹¹ The obtained ANN outputs were validated with the Original Outputs by performing Regression Analysis. The obtained model showed R2=0.81 overall which can be seen in Figure 6.

Figure 6 R² for training, validation, testing and all dataset (mm).

After numerous iterations of model training, testing, and validation, it was noted that the coefficient of determination of the model exhibits an upward trend with the augmentation of neurons. Conversely, augmenting the neuron count contributes to heightened model intricacy, particularly in the context of an equation encompassing eight input variables. Given that one of the principals aims of the investigation is the derivation of an equation, an optimal neuron count is imperative to strike a balance between model complexity and predictive accuracy. Three neurons are selected for the model development with R2 = 0.81. The model with optimum accuracy is reported in Table 3& 4 with the weights and bias matrices. An independent mathematical expression can be derived from the ANN architecture. The developed equation is presented in Equation 3. The equation has three tangent hyperbolic functions for representing three hidden neurons in MLP model.

Faulting  =4.75×(2.6472×TANH(-0.0000001×E+0.00063×P+0.6677×θ-0.0051×FT+0.03124 ×TS–2.6494×PT-0.0797×A-0.13237×OMC+ 4.26033)+2.57953×TANH(-0.0000003×E–0.0001×P–0.16106×θ+0.01318×FT–0.03512×TS+2.33426×PT+0.09709×A–0.58312×OMC+ 2.49604)–0.17844×TANH( 0.0000018×E+0.00151×P+0.46778×θ+0.02727×FT– 0.01262×TS–2.0751×PT–0.02091×A–0.88218×OMC+31.8459)- 0.72531+1)+0.1              (3)

Where,

E = ESAL (Equivalent Single Axle Load)     

P = Annual Precipitation (mm)

θ = Annual Average Temp (°C)        

FT = FT Cycle (days)

TS = Tensile Strength (psi)

PT = Pavement Thickness (mm)      

A = Pavement Age (yr)      

OMC = Optimum Moisture Content (%)

Sensitivity analysis of the developed ANN model

As the MLP has multiple inputs, the impact of each input parameter is measured by the sensitivity index. Equation 4 defines the sensitivity index. In this study the absolute value of the sensitivity index is measured. The sensitivity index is proportional to the variable impact on model output. Figure 7 shows the sensitivity of the input parameters to faulting.

Figure 7 Sensitivity index of input parameters.

$S=\left(\frac{O_2-O_1}{I_2-I_1}\right)\left(\frac{I_{ave}}{O_{ave}}\right)$       (4)

Where,

S= Sensitivity Index

O₂ = Maximum ANN Output of faulting

O₁ = Minimum ANN Output of faulting

I₂ = Maximum Input variables of faulting

I₁ = Minimum Input variables of faulting

I_ave = Average of Input variable of faulting

O_ave = Average of ANN Output of faulting

Faulting is more responsive to pavements thickness and Tensile Strength. Apart from these two variables, the other inputs show similar impacts on faulting.

With the help of machine learning approach, prediction model for faulting in Rigid Pavements for Dry-Freeze and Dry No-Freeze Climatic Zone was developed. For training the ANN model, 190 observations over the 30 years of lifespan were evaluated. Based on literature reviews four structural and four environmental parameters were selected which are ESAL, Annual Precipitation (mm), Annual Average Temp (°C), FT Cycle (days), Tensile Strength (psi), Pavement Thickness (mm), Pavement Age (yr), Optimum Moisture Content (%). By incorporating these environmental, structural, and traffic elements, the model aims to anticipate faulting in rigid pavements in dry region. Validation was done by comparing the model's predictions with actual field measurements, resulting in a commendable R-squared value of 0.8, indicating an 80% accuracy rate. The model can further improve by incorporating more observation over the years. Additionally, employing additional hidden layers with a greater number of neurons or exploring alternative methods for synthesizing the prediction model may yield more precise results. This predictive tool could prove invaluable for pavement managers and engineers, allowing them to preemptively address faulting issues, thus averting further pavement deterioration, and ensuring safer roads with optimal ride quality, all within budget constraints.

None.

The authors declare that there is no conflicts of interest.

1. Simpson L, Brent R, et al., Sensitivity analyses for selected pavement distresses, no. SHRP-P-393. 1994.
2. Ehsani M, Moghadas F, Hajikarimi P. Developing an optimized faulting prediction model in jointed plain concrete pavement using artificial neural networks and random forest methods. Int J Pavement Eng. 2022;24(2).
3. Ker HW, Lee YH, Lin CH. Development of faulting prediction models for rigid pavements using LTPP database. Statistics. 2008;218(0037):30–37.
4. Jung Y, Zollinger D, New laboratory-based mechanistic-empirical model for faulting in jointed concrete pavement. Transp Res Rec. 2011;2(2226):60–70.
5. Darter M, Khazanovich L, Yu T, et al. Reliability analysis of cracking and faulting prediction in the new mechanistic-empirical pavement design procedure. Transp Res Rec. 2005;1936:150–160.
6. Agurla M, Lin S. Long-term pavement performance automated faulting measurement. 2015.
7. Buscema M. Back propagation neural networks. Subst Use Misuse. 1998;33(2):233–270.
8. Jamal P, Ali M, Faraj RH, et al. Data normalization and standardization: a technical report. Mach Learn Tech Reports. 2014;1(1):1–6.
9. Aksu G, Güzeller CO, Eser MT. The effect of the normalization method used in different sample sizes on the success of artificial neural network model. Int J Assess Tools Educ. 2019;6(2):170–192.
10. Dubey SR, Singh SK, Chaudhuri BB. Activation functions in deep learning: a comprehensive survey and benchmark. Neurocomputing. 2022;503(7):92–108.
11. Ranganathan. The levenberg-marquardt algorithm 3 LM as a blend of gradient descent and gauss-newton itera. 2004;142:1–5.