Debris flows triggered by Merapi eruption in 2010 have impacts on the environment and social condition along the rivers on the volcano, especially in Pabelan River. Material resulted from debris flows could change on morphology and porosity of riverbed surface material, as well as the capacity of sediment. Therefore, it is important to study the influence of Merapi eruption in 2010 on environmental and social conditions in Pabelan River. To determine the river morphology was used Ronsgen method. To calculate porosity of riverbed surface material was used the equation was proposed by Sulaiman. Einstein equation was used to calculate sediment transport. To investigate the social conditions, damage land and sand mining activity were used as parameters. The result has shown that morphology types at confluence Progo-Pabelan Rivers, Srowol Bridge, and Pabelan Bridge 1 were D5b, D5b and E5, respectively. Sedimentation has occurred in the segment between the confluence of Progo-Pabelan Rivers and Srowol Bridge. Erosion has taken place in the segment between Srowol Bridge and Pabelan Bridge 1. The riverbank collapses took place along the river and it gave a negative impact on social conditions. The sand mining activity was intensive, and the activity has a positive impact on the economical inhabitants.

Keywords: the 2010 Merapi eruption, environment, social condition, Pabelan River

Pabelan River is located in the west side of Merapi, and one of the Progo river’s tributaries with a length of around 46 kilometers and it flows from Merapi Volcano to the south direction.¹ It is very important for the local community's livelihood. Most of the villages are located in the river is very dependent on the natural resources of the river Pabelan. Pabelan River is one of the rivers that are passed by the debris flow from Merapi eruption. Damage due to debris flows has caused changes in the river morphology of Pabelan and the surrounding ecosystem. Material deposition of debris flow from the eruption of Merapi in 2010 change the morphology and porosity of the sediment at the bottom of the Pabelan River and sediment transport capacity. In addition, debris flow has also affected the social and economic conditions around the Pabelan River.

Therefore, it is important to study the influence of Merapi eruption in 2010 on environmental and social conditions in Pabelan River. The study aims to investigate the river environmental and social conditions in Pabelan River due to debris flows. The research was conducted in three locations, they are Pabelan Brigde (C), Srowol Brigde (B), and conjunction of Pabelan-Progo (A), as shown in Figure 1.

Figure 1 The research locations.

River morphology

River morphology is related to the physical condition of the river geometry, the type, nature, and behavior of the river with all aspects of the changes in space and time dimensions, thus involving the dynamic nature of the river and its environment are interrelated with each other.² In the determining of river morphology is needed geometry data, covering a wide river, depth, cross the river, the coordinates of the location and slope of the riverbed. According to Rosgen³ types of river morphology are shown in Figure 2.

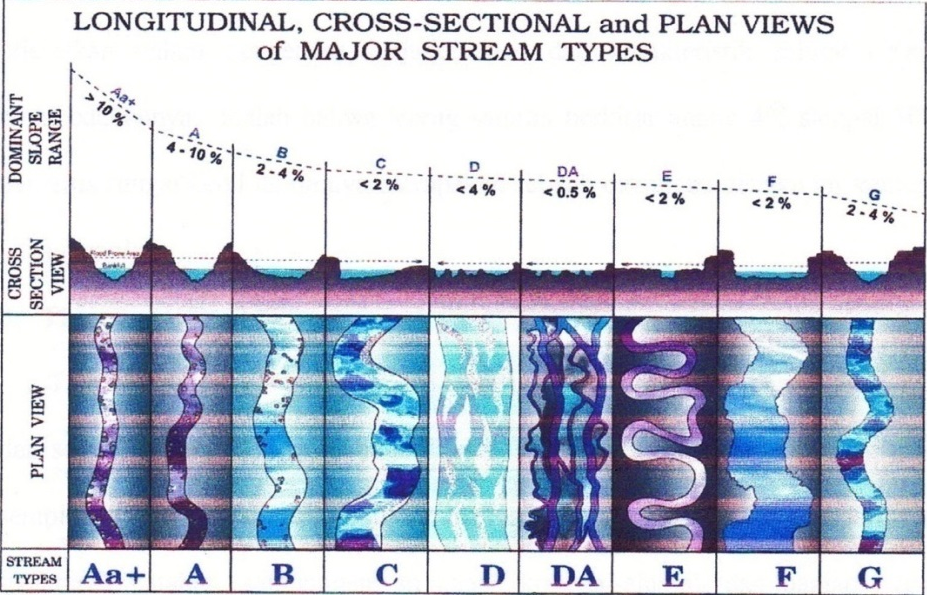
Figure 2 Morphology types by Rosgen.³

The steps that used to determining river morphology according to the Rosgen,³ as follows:

Entrenchment ratio

Entrenchment Ratio is the relationship of the flood prone area width (Wf_pa) and the ratio of the Bank full Surface Width (W_bkf). The way to measure in determining Entrenchment Ratio (ER) is:

$ER=\frac{\text{Flood Prone Area Width }\left(W_{fpa}\right)}{\text{Bankfull Surface Width }\left(W_{bkf}\right)}$ (1)

Width/depth ratio (W/D ratio)

Width width/Depth Ratio is the relation between the width of the river (W_bkf) and the depth ratio relation (d_bkf). The formulation used is:

$W/D Ratio=\frac{W_{bkf}}{d_{bkf }}$ (2)

Furthermore, the calculated slope river and riverbed material “D₅₀”. “D₅₀” is diameter in 50 percent of population sediment sample that is observed to represent of sediment particle diameter in that location.

Sediment transport

Sediment transport is a material transport phenomenon in the watershed. The shape, size and weight of the material determine the massive of amount sediment transport. There are many formulas that can use to account scale of sediment transport; one of them is Einstein’s Formula.⁴ Einstein determines the sediment transport equation that links the base material/bed material and local flow. The equation describes equilibrium state of the granular based exchange between the base layer (layer bed) and its riverbed. Einstein use d₃₅ as transport parameters, whereas for roughness use d_65. In determining scale of sediment transport that use Einstein’s Formula, the necessary data are: flow rate (Q), the width of the channel/river (B), the slope of the river (S), gradation of grain size sieve analysis and viscosity of water/water viscosity (v). Steps to be able to calculate the sediment transport need to determine the grain size d₃₅ and d₆₅. Then the sediment transport can be calculated with the following steps.

Friction velocity due to grain roughness

$\underset{\dot{}}{u}\text{'} = \surd g.Rb’.S$ (3)

Sub-viscous height

$\delta \text{'}=\frac{11,6 . \upsilon }{\underset{\dot{}}{u}\text{'}}$ (4)

$\frac{ks}{\delta \text{'}}=\frac{d65}{\delta ΄}$ (5)

$\Delta = \frac{d65 }{\delta ΄}$ (6)

Average of discharge velocity

$V=5,75.\text{ <munder> u <mo>˙</mo> </munder> '}.log(12,27)\frac{Rb\text{'}.x}{ks}$ (7)

Stream intensity

$\Psi = \frac{\gamma \mathfrak{s}-\gamma }{\gamma } \frac{d35}{S.Rb\text{'}}=1,65 \frac{d35}{S.Rb\text{'}}$ (8)

By using Einstein-Barbarosa diagram, it can be obtained the value U’/V that it can use to know U’.

Hydraulic diameter due to bed channel configuration

$R_b”= \frac{\left(U\text{'}\right)²}{gS}$ (9)

$R_b=R_b’+R_b”$ (10)

Controlling by discharge calculation

$Q=AV=(BhU΄)$ (11)

Sediment discharge

${\left(i_b{q}_b\right)}_{}=i_b\theta .{\gamma }_s{\left(gd\right)}^{3/2}{()}^{1/2}$ (12)

Q_sed = ${{\displaystyle \sum }}^{\text{}}{i}_b{q}_b$ (13)

Porosity of riverbed material

According to Sulaiman,⁵ to calculate a value of riverbed sediment porosity is done with the following steps. First, the bed material on each point representing top, middle and bottom material is sieved to obtain grain size distribution. Furthermore, a type of sediment distribution is determined based on the value of γ and β parameters, which is calculated by the following equations:

$\gamma =\frac{log d_{max}-\log d_{50}}{log{d}_{max-}\log d_{min}}$ (14)

$\beta =\frac{\log d_{max}-\log d_{peak}}{\log d_{max}-\log d_{min}}$ (15)

Once the values of γ and β are known, the type of grain size distribution can be found using the diagram proposed by Sulaiman,⁵ as shown in Figure 3. Furthermore, the porosity values can be calculated with the following equation:

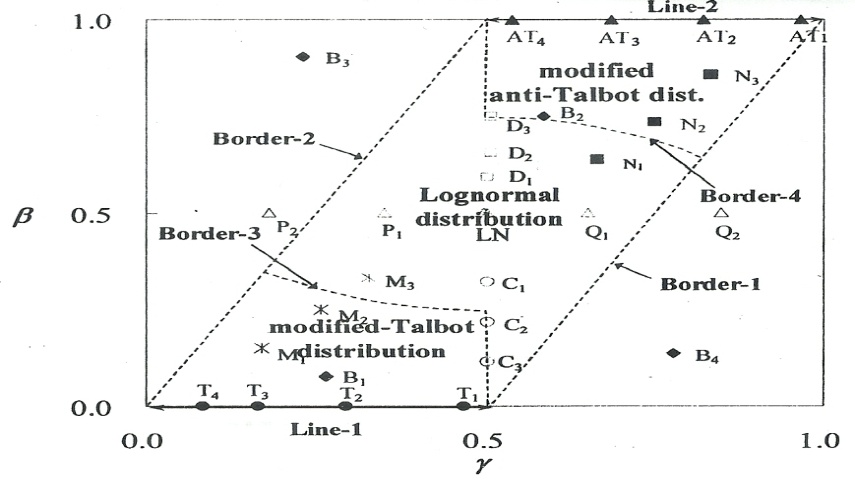
Figure 3 Diagram to determine type of grain size distribution.⁵

Lognormal distribution

${\sigma }_{1 }{}^2\underset{j=1}{\overset{N}{{\displaystyle =\sum }}}\left(In{d}_{j }-Ind\right)²P_{sj}$ (16)

Where:

$\gamma =0.1561,if1.5<\sigma$

$\gamma =\left(0.0465\sigma \right)+\left(0.2258\right) ,$ , $if1.25<\sigma <1.5$

$\gamma =\left(-0.141\sigma \right)+\left(0.3445\right),$ if $1.0<\sigma <1.25$

$\gamma =\left(-0.105\sigma \right)+\left(0.3088\right)$ , if $0.75<\sigma <1.0$

$\gamma =\left(-0.1871\sigma \right)+\left(0.3698\right)$ , if $0.5<\sigma <0.75$

M Tallbot distribution

$n_T\left(x\%\right)=\frac{In\left(f\left(D_{x\%}\right)\right)}{In\left(\frac{\log D_{x\%}-\log D_{\min }}{\log D_{\max }-\log D_{\min }}\right)}$ (17)

$n_T=\frac{n_T\left(16\%\right)+n_T\left(25\%\right)+\left(50\%\right)+n_T\left(75\%\right)+n_T\left(85\%\right)}{5}$

$100\le d_{maks}/d_{min},\gamma =0,0125n_T+0,3$

$d_{maks}/d_{min}\ge 1000,\gamma =0,0125n_T+0,15$

Socio-economical aspects

Socio-economical parameters used in this study are infrastructure damage and sand mining activities. Debris flows will give negative impacts on social conditions as well as positive impacts. The negative impacts that often occurred are river bank collapse due to erosion along the river. Damage in a river bank, it will cause the social problem, such as the loss of agricultural land, houses damaged and others. Nevertheless, debris flows also brought positive impacts, such as the material could be used as resources, so that mining activities can improve inhabitant economy.

Stages of the study to determine the debris flow effect post eruption of Merapi in 2010 on Pabelan River, especially the environmental and social conditions are as follows:

Data collection

The data collected is primary and secondary data. The primary data consists of a cross-section and dimensions, river slope, sediment samples, sand mining activities and river bank collapses. Secondary data includes topographic maps and social economic data.

Laboratory test

Laboratory testing is used to determine the grain size gradation of the riverbed material sample.

Data analysis

Based on the data from the field survey and the laboratory test, river morphology, porosity and sediment transport were analyzed. In addition, also land degradation/river bank collapse and sand mining activities were analyzed.

Discussion and conclusion

Based on the analysis data, then discussion of the results and conclusion were carried out. The parameters used to determine effects of debris flow due to the eruption of Merapi in 2010 on environmental conditions is river morphology, porosity of riverbed sediment and sediment transport. River morphology determination method used,³ sediment porosity using the formula of⁵ and to determine the amount of sediment transport with Einstein's formula. The parameters used to determine social conditions are inhabitant evacuated, infrastructure damage and sand mining activities. The location of the study were conducted in three locations Pabelan River, namely at the conjunction between Pabelan and Progo Rivers, Srowol Bridge, and Pabelan Bridge. The detail of locations is shown in Table 1. Figures 4–6 describes the situation in the research locations.

Figure 4 River condition at Conjunction of Pabelan and Progo Rivers.

Figure 5 River condition at Srowol Bridge.

Figure 6 River condition at Pabelan Bridge.

River morphology

Based on Rosgen³ method, morphology types of rivers are shown in Table 2. It can be seen from Table 2 that the morphology type in Pabelan River generally is D5. It indicates that flow in the tributaries is multi flow. Only at Pabelan Bridge, the river morphology is E5, which means single flow. Riverbed material in Pabelan River is sand, and its mean diameter varies between 0.5mm to 0.88mm.

Porosity of sediment

Based on the results, the value of γ and β parameters are shown in Table 3. Table 3 shows that for Pabelan River, a type of grain size in the upstream area is Talbot with a porosity of 0.29. In the downstream area of Pabelan River, type grain size is log normal with a porosity value of 0.15.

Sediment transport

Based on calculations using Einstein formula, sediment transport for each location in Pabelan River is shown in Table 4. Sediment transport the location in Pabelan River shows the same relative value. This indicates that there is no erosion or deposition. Material transported in the River Pabelan, generally derives from Mount Merapi.

Socio-economic aspects

Land degradation and sand mining activity are used as social parameter for assessing Merapi eruption effect in Pabelan river area. According to the resulting survey at the location, land degradation almost occurred in every observation point. It bothering some of land settlement and local farming activity. Some local settlements were buried by containing cold volcanic mudflow materials. Riverbank erosion occurred at those sites that make the settlement and local farming damage, as shown in Figure 7. In addition to giving the negative impact, debris flow also provides benefits to the potential of the material for sand mining. Based on the survey, in almost all the locations, there are sand mining activities, with a small to medium scale. The intensity of sand mining has tendency greater if compared with before the eruption of 2010. Figure 8 shows a sand mining activity at Srowol Bridge in Pabelan River.

Figure 7 Riverbank collapse at the conjunction between Pabelan-Progo River.

Figure 8 A sand mining at Srowol Bridge in Pabelan River.

According to the research, environment and social changes occurred at Pabelan river after Merapi eruption 2010. Sediment transport at Pabelan bridge showing the smallest value than the other observation point. The surface of the riverbed material value tendency becomes smaller at the downstream. The surface of the riverbed material at the upstream area has harder tendency compare with the downstream area. Land damage occurred at three observation points caused by sediment eruption.

Nomenclature

Wf_pa             = flood-prone area width

W_bkf               = bank full surface width

W_bkf          = bank full surface width

d_bkf                 = bank full mean depth

D₅₀                = diameter in 50 percent of population sediment sample

ự              = friction velocity due to grain roughness

g              = gravity

Rb’         = hydraulic diameter due to grain roughness

S              = bed channel slope

δ'             = sub-viscous layer height

v              = viscosity

ks            = grain size diameter

Δ             = bed channel roughness

V             = mean velocity

Ψ             = stream intensity

d              = grain size diameter

γs            = specific gravity of water

γ              = specific gravity of sediment

Rb”         = hydraulic diameter of bed channel configuration

Q             = discharge

A             = cross section area of river/channel

V             = velocity

B             = channel/river width

h              = water depth

(ibqb)     = sediment discharge of each fraction

ib             = percentage of material in population

θ              = slope value at Einstein diagram

γ and β = geometrical parameter

d_max         = maximum diameter

d_min          = minimum diameter

d_peak        = peak diameter

σ              = deviation standard

d              = grain size diameter

j               = grain size class

psj           = proportion of class j

γ              = porosity

f(D)         = cumulative percentage of grain size

n_T            = Talbot number

None.

None.

The authors declare there are no conflicts of interest.

1. Winditiatama S. Characteristics of downstream area of Pabelan River Post Merapi Eruption in 2010. Thesis, Diploma Program of Civil Engineering Department, Yogyakarta: Gadjah Mada University; 2011.
2. Infrastructure in River. 2012.
3. Rosgen D. Applied river morphology, widland hydrology. Colorado: Pagosa Springs; 1996.
4. Kironoto BA. Sediment transport hydraulics. Civil Engineering Department, Graduate School Program, Yogyakarta: Gadjah Mada University; 1997.
5. Sulaiman M. Study on porosity of sediment mixtures and a Bed-porosity Variation model. PhD dissertation, Civil and Earth Resources Engineering Department, Kyoto: Kyoto University; 2008.