This study is the first to develop allometric models for estimating above-ground biomass (AGB) and below-ground biomass (BGB) of individual trees based on destructive sampling procedures in the montane tropical forests of Central Africa. As Cameroon is committed to Reducing Emissions from Deforestation and Forest Degradation (REDD) initiatives, it is particularly important for the country to develop such models. The data used for the modeling covered a wide range of tree species (34) and diameters at breast height (dbh) from 6 to 117 cm. The AGB and BGB models were developed from 60 and 30 tree samples, respectively. The developed AGB models explained a large part of the biomass variation (Pseudo-R2 0.80-0.87) and performed well when tested over different size classes. A model with dbh, basic wood density and total tree height (h) as independent variables is generally recommended for application if appropriate information on h is available. Tests of previously developed AGB models with modeling data, where large mean prediction errors occurred, generally demonstrated the importance of developing local models. BGB models performed reasonably well over different size classes, and biomass per unit area will probably be appropriately estimated when applying them. Some of the challenges related to the estimation BGB for small trees mean, however, imply that, the models may need to be recalibrated if more data becomes available.

Keywords: biomass, roots, leaves, twigs, branches, root-shoot ratio

Climate change over the last few decades has increased the need for information on the amount of plant biomass present in a given ecosystem¹ and requires reliable estimates of the carbon stock in different ecosystems.^2–4

According to scientists, in order to stabilize the climate by 2050 and prevent it from becoming 2° Celsius warmer than in 1970,⁵ total greenhouse gas emissions from all countries need to be halved. To achieve this, a range of solutions has been proposed. These all are based on the principle of reducing anthropogenic emissions and increasing the storage potential of carbon sinks.

According to Poulsen et al.,⁶ Black Africa is a stakeholder in climate negotiations because it is home to the world's second largest forest massif: the Congo Basin. These forests store large quantities of carbon and therefore require precise allometric regressions for their estimation.

Generally speaking, forest biomass estimates in tropical rainforests are interesting for several reasons. Firstly, to understand basic properties of forest conditions such as productivity and structure.^7,8 Biomass is also important for estimating the amount of carbon dioxide sequestered in forests.^9–11 The amount of biomass varies between different forest types, but also between sites within forest types due to different climatic conditions, soils, altitudes, history of land use and human disturbances.¹² The amount of biomass for individual trees varies with factors such as size (diameter at breast height (dbh) and tree height (h), wood basic density (dry mass weight over green volume), tree species, branching patterns and tree shape.^9,11,13,14 There are two main approaches for estimating biomass based on forest inventory data: 1) using allometric biomass models or 2) using volume equations combined with expansion factors.¹⁵ The combination of volume equations and expansion factors to estimate biomass is to some extent still used¹⁶ but by far the most common approach is to estimate biomass through allometric models based on easily measurable variables such as dbh, h and other tree variables.^9–11 Provided that information on individual trees is available, and that appropriate models exist, this is generally the most straightforward and best way to quantify biomass. However, it is also important to note that the choice of allometric models is the most important source of error in biomass estimation for tropical forests.^16,17

Numerous allometric models which estimate aboveground biomass (AGB, in kg dry mass) of trees, have been developed for tropical forests in sub-Saharan Africa. A recent review of models for this region¹⁸ revealed that for tropical rainforests (tropical moist forests) quite many species- specific models while fewer general models covering multiple tree species existed. Examples of well- documented general models estimating AGB for rainforests, however, are provided from Cameroon,^19,20 Ghana,²¹ Gabon²² and Madagascar.²³ To our knowledge no biomass models have been developed for tropical rainforests in central Africa. Pantropical biomass models have also been developed⁹ and used for estimating AGB for rainforests in the region, but no data from Africa were available for the development of these models. However, improved models for estimating AGB comprising data also from this continent have recently been developed.¹¹ In addition to biomass from stem, branches and twigs/leaves, a tree also consists of belowground biomass in root crown and roots. Since excavation of belowground biomass is very laborious, few models for estimating belowground biomass (BGB, in kg dry mass) of trees have been developed. The only example that we know from tropical rainforests is provided by Liu et al.,²⁴ in Cameroon, where 14 trees from six different species were used to develop models, however, they focused on trees from plantations and previously logged secondary forests.

As to date, there are no specific models for estimating BGB, so the recommended estimation method is to multiply AGB estimates and root to shoot ratios (RS-ratio) to obtain BGB estimates.^25–27 This method, however, is considered relatively inaccurate due to for example different edaphic factors or soil conditions that influence root allometry.²⁸

The Cameroon's tropical rainforests cover an estimated 22,5 million hectares²⁹ which include dense evergreen and semi-evergreen rainforests at low and medium altitude, submontane and montane, as well as mangroves. To date, only submontane forests are the least known, and no biomass model has been developed for these tropical rainforests. Also, Cameroon has recently started the first sample plot based national forest inventory.³⁰ At the same time, Cameroon is involved in initiatives to Reduce Emissions from Deforestation and forest Degradation (REDD), which requires the development of biomass models estimating AGB and BGB. In addition, fuel wood and fodder from branches, twigs and leaves are important limited resources that should be inventoried. Biomass models estimating such resources are therefore also desirable.

The main objective of this study was to develop allometric models for estimation of AGB and BGB of individual trees for rainforests in Cameroon. We also tested pantropical models^9,11 and local models from Africa^13,14,23,31 on our modelling data. In addition, models for estimating AGB for tree components such as stems, branches, and twigs/leaves, and statistics on RS-ratios were presented.

Study area and selection of sample trees

Data collection was carried out in the submontane forest located between 4° 04′ 23″ North and 9° 06′ 57″ East on Mount Etinde (1713 m). This is a submontane forest with continuous crowns that can only be found on this mountain. This forest is characterized by a closed stand with medium-sized trees (25-30 m tall) whose tops are more or less contiguous. Floristically, the most characteristic trees are from the Sapotaceae, Guttiferae, Sterculiaceae, Meliaceae, Olacaceae, Flacourtiaceae and Euphorbiaceae families (Figure 1).

Figure 1 Location of Mount Etinde, South-west, Cameroon.

Trees were sampled following the orientation of the four cardinal points. To ensure variation in tree allometry and basic wood density, trees were selected over a wide diameter range from 15 cm to 270 cm. Neither proximity to roads nor harvesting activities influenced tree selection.³² Thirty (30) of the 60 trees were selected for BGB measurements. The selection of these trees followed similar criteria to those of the trees selected for BGB determination.

Prior to felling, the diameter at breast height (dbh) and height (h) of all sample trees were measured. dbh measurements of the sample trees were taken using a calliper or diameter tape. For trees with buttresses extending the dbh measuring point, diameter was measured 30 cm above the buttress.³³ Tree heights were measured by using a Vertex hypsometer. Summary statistics of the trees are shown in Table 1.

Destructive sampling and laboratory procedures

The point of demarcation between aboveground and belowground biomass components were at a stump height of 30 cm. The aboveground part was divided into three components: stem, branches, and twigs/leaves. Stems (from the stump to the point where the first large branch protrudes the stem) and branches (diameter cut-off between branches and twigs was 2.5 cm) were cut into measurable billets with lengths of 0.2-1.5 m depending on their weight. Thereafter each billet was weighed separately for green mass using a spring balance (0.1 kg accuracy). Twigs and leaves were tied into bundles and weighed for green mass.

Full excavation of all belowground parts of trees is very demanding in terms of time consumption. Since resources for field work are limited, a choice has to be made between excavating a few roots in full²⁴ and to apply root sampling procedures to obtain data for a larger number of individual root systems.³⁴ In such procedures, only a number of roots from each root system are fully excavated, and then the information from the excavated roots is used to estimate biomass also for the roots not excavated.

In the present study, we generally followed the root sampling procedures as described by Tchinmegni & Djeukam.³⁵ For each root system, three main roots (small, medium and large) were selected from the root crown, measured for basal diameter, then traced to a minimum diameter of 1 cm and weighted for green mass. Similarly, a maximum of three side roots (small, medium and large) were selected from the excavated main roots, measured for basal diameter, traced to a diameter of 1 cm and weighted for green mass. Finally, all basal diameters of unexcavated main roots originating from the root crown, and all basal diameters of unexcavated side roots originating from main roots, were measured.

The excavation of the main roots was carried out by first removing top soil around the trees up to where all main roots originating from the root crown were partially exposed. This procedure was important for reducing work load of selecting main sample roots. The basal diameters of main sample roots were measured by using a diameter tape rather than a calliper because the roots tended to be oval in shape. When main roots encountered obstacles (stone or another tree); the diameters at the breakage point were also measured. Three samples from each tree were collected from each tree components (stem, branches, twigs/leaves, root crowns and roots) for laboratory analyses. The green mass weights of the samples were determined by using an electronic balance (0.001 kg accuracy) while in the field. The wood samples were oven dried in a laboratory with a temperature of 105°C,³⁶ with interval monitoring of four hours until they attained constant weights, then their dry mass weights were determined immediately by using an electronic balance. For each wood sample, the dry to green ratio (DG-ratio) was determined by dividing dry mass weight with green mass weight. Wood basic density values were not determined from the wood samples.

Data processing

All data processing and analyses were carried out with R software. For the aboveground components of the trees, the total green mass weights of each tree component were multiplied by their respective average DG-ratios to obtain the component dry mass weights. The total AGB was found by summation of dry mass weights from stem, branches and twigs/leaves. On average, 54 %, 39% and 7% of AGB were distributed to stems, branches, and twigs/leaves, respectively. The mean total AGB of the sampled trees was 2453 kg while the minimum and the maximum were 11 kg and 10603 kg, respectively. A scatter plot of total AGB versus dbh is shown in Figure 2 (upper panel). The BGB of trees was computed as follows:

1. A side root model was first developed by regressing green mass weights (Y, kg) and basal diameters (D, cm) of all selected side roots. We decided to apply a power law model, which is a general model describing organism allometry.³⁷ The side root model ($Y=1.19466*D^{1.09143}$ , n = 55, RMSE = 5.2kg, Pseudo-R² = 0.50, MPE% = 1.2, where RMSE, Pseudo- R² and MPE% are defined in Section 2.4) was then utilized to estimate green mass weights of unexcavated side roots and unexcavated parts (broken) of main roots.
2. Total green mass weights of main roots were found by summing the estimated weights of the side roots, the estimated weights of broken parts of the main root (if broken), the weights of the excavated side roots and the weights of the excavated parts of the main root.
3. Similarly, a main root model was developed by regressing total green mass weights (Y, kg) and basal diameters (D, cm) of all main roots. The main root model ($Y=0.37124*D^{1.74809}$ , n = 87, RMSE = 27.1kg, Pseudo-R² = 0.78, MPE% = 0.2) was utilized to estimate green mass weights of unexcavated main roots originating from the root crown.
4. Total green mass weights of all roots were found by summing the estimated weights of the main roots not excavated and the weights of the excavated main roots.
5. Finally, the conversion of root and root crown green mass weights to dry mass weights was done by multiplying green mass weights by the respective average DG-ratios. Thereafter, root and root crown dry mass weights of each tree were summed to total BGB. A scatter plot of BGB versus tree dbh is shown in Figure 2 (lower panel).

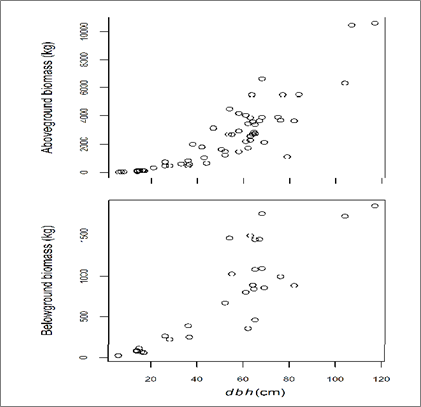
Figure 2 Relationships between dbh (cm) and aboveground biomass (upper panel, n=60) and belowground biomass (lower panel, n=30).

Model development and evaluation

Initially we tested many different model forms. However, we decided to apply the following frequently used nonlinear models (e.g. Henry et al.,¹³) to fit the AGB and BGB data:

$B=a*db{h}^b$   (1)

$B=a*db{h}^b*{\rho }^d$   (2)

$B=a*db{h}^b*h^c$   (3)

$B=a*db{h}^b*h^c*{\rho }^d$   (4)

Where B = dry mass in kg, dbh = diameter at breast height (cm), ρ = wood basic density, h = total tree height (m), a, b, c and d = model parameters to be estimated. The global wood density (GWD) database^38,39 were accessed to obtain values for individual species for model development and where needed in this study. When ρ was available from several sites for a certain tree species we used the average values. The PROC NLIN procedure in SAS was applied to estimate the parameters of the models. A broad range of initial values for the model parameters were tested to ensure global convergence solutions.

The precision of the models was evaluated by means of the root mean square error (RMSE), Pseudo- R² and statistical significance of model parameter estimates. Models with parameter estimates not significantly different from zero (p > 0.05) were not evaluated further. These were computed as follows;

$RMSE={\left(\frac{SSR}{n}\right)}^{1/2}$   (5)

$Pseudo-R^2=1-\left(\frac{SSR}{CSST}\right)$   (6)

Where SSR = Sum of residuals squares, CSST= Corrected total sum of squares, and n = number of observations.

Further evaluations of the models were also done by means of mean prediction errors (MPE);

$MPE=\Sigma \frac{e}{n}$   (7)

$MPE\%=\left(\frac{MPE}{MOB}\right)*100$   (8)

Where MPE are residuals (differences between estimated and observed biomass), and MOB is mean observed biomass (Table 2).

Biomass models for different tree components and corresponding fit statistics are shown in Table 3. For the total AGB models, model fit increased only slightly when ρ was included as independent variable in addition to dbh (model 2) as compared to model 1. The inclusion of h (model 3), and h and ρ (model 4) improved fit statistics. For the stem biomass models, inclusion of h (model 3) was associated with largest improvement in fit statistics while including ρ had less effect (models 2).

When dbh, h and ρ were used as independent variables, the parameter estimate for ρ was not significantly different from zero. The branches and twigs/leaves models had generally lower fit statistics compared to the total AGB and stem models. The overall MPE% for the models varied between -4.5% and 3.4%, but none were significantly different from zero. For total AGB model 1, MPE values significantly different from zero (α = 0.05) appeared for one dbh class and one h class (Table 4). No differences were significantly different from zero for other models. Although not significantly different from zero, the MPE% values for small trees were relatively high for model 2 and model 3. Model 4 had lower MPE% values as compared to all the other models and no pattern were seen over the size classes. For the BGB models, adding ρ in addition to dbh (model 2) as compared to when dbh was the only independent variable (model 1), fit statistics improved considerably. When adding h as independent variable in addition to dbh and ρ (model 4), only small improvements in the fit statistics were obtained. The performance of BGB models on modelling data is presented in Table 6. The overall MPE% values were relatively small and not significantly different from zero, however, all models significantly over estimated biomass for the smallest trees according to dbh class.

The MPE values for previously developed AGB models are shown in Table 5. The Chave et al.,⁹, Chave et al.,¹¹, Henry et al.,¹³ and Fayolle et al.,²⁰ were significantly over estimated biomass while MPE values were not significantly different from zero for the Vellidient et al.,²³ and Ngomanda et al.,¹⁴ models.

The mean RS-ratio of trees sampled for both AGB and BGB was 0.49 and varied from 0.14 to 2.24. A simple log-linear regression model showed that RS-ratio decreased with increasing dbh (Figure 3).

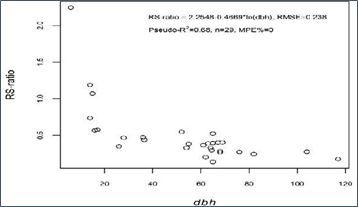
Figure 3 Relationship between dbh (cm) and RS-ratio (n=30).

This study was the first to develop models estimating AGB and BGB for rainforests in central Africa based on destructive sampling procedures. The 60 sample trees used for the modelling was fewer than 100 recommended as a minimum by Vorster et al.,⁴⁰ but more than in most models.^17,41,42 The inclusion of large data ranges regarding tree size is of particular importance in tropical forests because large trees usually account for a very large part of the biomass.³⁵ However, heavy work load and restricted funding prevented us from collecting trees larger, in this case, trees exceeding dbh of 117 cm, but at least including the most frequent and rare tree species. All models for total AGB models had parameter estimates different from zero and reasonably good fit statistics (Pseudo-R² ranging from 0.80-0.87) (Table 3). They also behaved relatively well when tested over different size classes (Table 4). As such all the models can reasonably be applied for estimating biomass. The inclusion of all three independent variables (model 4), improved considerably model fit, and behaved well over all size classes while the other models tended to overestimate biomass for the smallest trees based on dbh and h. If all tree variables are available, we therefore recommend model 4 to be applied.

Many authors have argued for the inclusion of h as an independent variable in biomass models. Manolopoulos et al.,⁴³ for example, argued that inclusion of h has the advantage of expanding the applicability of models because height-diameter relationships depend on environmental conditions, which vary between sites.⁴⁴ Rarely h for all trees is available from forest inventory. The general height-diameter models for different forest types including rainforests have been developed for Cameroon.¹⁶ Although we generally recommend model 4 to be applied, one should be aware that the use of an estimated h in biomass models will introduce additional errors. However, the accuracy of tree h measurements in closed-canopy forests can be poor.^45,46 The accuracy of the estimated or measured h should therefore be carefully considered in the choice between model 2 and 4 when estimating total AGB.

The performance of the previously developed AGB models on our modelling data (Table 5) generally demonstrated the importance of developing local models. The relationship between biophysical properties of trees and biomass is affected by site and regional conditions, so it is not surprising that models fitted with data closer to a test site are more precise; and that model fitted with data from large geographical ranges, such as pantropical models, could also yield relatively large errors for locally.^47,48 Exact reasons for the deviations are difficult to identify. Tucker et al.,⁴⁹ regarded the selection of sample trees as a major source of uncertainty in model development and claimed that the trees are probably never selected at random, but instead are often selected near roads (i.e. are they representing the entire area?) and in relation to logging activities (i.e. are the trees with the best form selected?). Djomo et al.,⁵⁰, Henry et al.,¹³ and Fayolle et al.,²⁰ selected sample trees in relation to logging activities. Duncanson et al.,⁵¹ and Chave et al.,¹¹ also pointed out measurement errors and destructive sampling procedures as important sources of uncertainty in the development of biomass models. Measurements of dbh and h in tropical rainforest are challenging and associated with errors. In some studies, biomass of the lower parts of large trees was determined from volume based on geometrical measures and wood specific gravity (e.g. Fayolle et al.,²⁰). In the present study selection of sample trees was not influenced by closeness to roads or harvesting activities and all tree parts were weighted. The most likely explanation for the deviations between the estimated AGB from the previously developed models and our observed values is the actual differences in tree biomass quantities due tree shape that could have been influenced by the heavy commercial harvestings that took place in periods before 1990, where possibly large proportions of the well-shaped and big trees were preferred. The mean RS-ratio of trees selected for BGB modelling was 0.49. Variation in mean RS-ratios for different tropical rainforests has previously been reported.²⁵ The pattern of decreasing ratio with tree size agrees well with previous results from miombo woodland in central Africa.⁴⁴ The mean RS-ratios frequently are recommended for estimating BGB.⁵² However, if a fixed mean RS-ratio is used for a relationship that most probable is nonlinear (Figure 3), a bias will be introduced. Therefore, RS-ratios depending on dbh should be applied to estimate BGB for individual trees. The BGB models were significantly over estimated biomass for the smallest trees (Table 6). Since large trees usually account for a very large part of the biomass in rainforests,³⁵ biomass per unit area will probably be reasonable estimated when applying these models. If data for BGB become available, in particular for the size ranges with few observations, the models for BGB could be further tested and possibly recalibrated.

The model with dbh, ρ and h as independent variables is generally recommended for AGB if accourate information on h is available. The previously developed AGB models had large mean prediction errors; this demonstrates the importance of local models. Challenges related to the over estimation of BGB for small trees, implied that models should be further tested and possibly recalibrated, if more BGB data become available.

None.

None.

The authors declared that there is no conflict of interest.

1. Cavicchioli R, Ripple WJ, Timmis KN, et al. Scientists’ warning to humanity: microorganisms and climate change. Nature Reviews Microbiology. 2019;17(9):569–586.
2. Schulte‐Uebbing L, de Vries W. Global‐scale impacts of nitrogen deposition on tree carbon sequestration in tropical, temperate, and boreal forests: A meta‐analysis. Global Change Biology. 2018;24(2):e416–e431.
3. Abbas S, Wong MS, Wu J, et al. Approaches of satellite remote sensing for the assessment of above–ground biomass across tropical forests: Pan–tropical to national scales. Remote Sensing. 2020;12(20):3351.
4. Pascual LS, Segarra–Medina C, Gómez–Cadenas A, et al. Climate change–associated multifactorial stress combination: A present challenge for our ecosystems. Journal of Plant Physiology. 2022;153764.
5. Layachi OB. The Impact of global warming on climate change and the role of the paris agreement in maintaining the rate of temperature rise. PalArch's Journal of Archaeology of Egypt/Egyptology. 2021;18(17):317–344.
6. Poulsen JR, Medjibe VP, White LJ, et al. Old growth Afrotropical forests critical for maintaining forest carbon. Global Ecology and Biogeography. 2020;29(10):1785–1798.
7. Huang L, Zhou M, Lv J, et al. Trends in global research in forest carbon sequestration: A bibliometric analysis. Journal of Cleaner Production. 2020;252:119908.
8. Malhi Y, Girardin C, Metcalfe DB, et al. The Global Ecosystems Monitoring network: Monitoring ecosystem productivity and carbon cycling across the tropics. Biological Conservation. 2021;253:108889.
9. Chave J, Andalo C, Brown S, et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia. 2005;145:87–99.
10. Henry M, Picard N, Trotta C, et al. Estimating tree biomass of sub–Saharan African forests: a review of available allometric equations. Silva Fennica. 2011;45:477–569.
11. Chave J, Réjou–Méchain M, Búrquez A, et al. Improved pantropical allometric models to estimate the above ground biomass of tropical forests. Global Change Biology. 2014;20:3177–3190.
12. Mo L, Zohner CM, Reich PB, et al. Integrated global assessment of the natural forest carbon potential. Nature. 2023;624(7990):92–101.
13. Henry M, Besnard A, Asante WA, et al. Wood density, phytomass variations within and among trees, and allometric equations in a tropical rainforest of Africa. Forest Ecology and Management. 2010;260:1375–1388.
14. Ngomanda A, Obiang NLE, Lebamba J, et al. Site–specific versus pantropical allometric equations: Which option to estimate the biomass ofa moist central African forest? Forest Ecology and Management. 2014;312:1–9
15. Magalhães TM, Cossa VN, Guedes BS, et al. Species–specific biomass allometric models and expansion factors for indigenous and planted forests of the Mozambique highlands. Journal of Forestry Research. 2021;32(3):1047–1065.
16. Kafuti C, Van den Bulcke J, Beeckman H, et al. Height–diameter allometric equations of an emergent tree species from The Congo Basin. Forest Ecology and Management. 2022;504:119822.
17. Schindler Z, Seifert T, Sheppard JP, et al. Allometric models for above–ground biomass, carbon and nutrient content of wild cherry (Prunus avium L.) trees in agroforestry systems. Annals of Forest Science. 2023;80(1):28.
18. Mankou GS, Ligot G, Panzou GJL, et al. Tropical tree allometry and crown allocation, and their relationship with species traits in central Africa. Forest Ecology and Management. 2021;493:119262.
19. Djomo AN, Chimi CD. Tree allometric equations for estimation of above, below and total biomass in a tropical moist forest: Case study with application to remote sensing. Forest Ecology and Management. 2017;391:184–193.
20. Fayolle A, Ngomanda A, Mbasi M, et al. A regional allometry for the Congo basin forests based on the largest ever destructive sampling. Forest Ecology and Management. 2018;430:228–240.
21. Brown HC, Berninger FA, Larjavaara M, et al. Above–ground carbon stocks and timber value of old timber plantations, secondary and primary forests in southern Ghana. Forest ecology and management. 2020;472:118236.
22. Ekoungoulou R, Mikouendanandi MRBE, Liu XD. Carbon storage in an intact republic of Congo’s forest. Applied Ecology & Environmental Research. 2021;19(1).
23. Vieilledent G, Vaudry R, Andriamanohisoa SFD, et al. A universal approach to estimate biomass and carbon stock in tropical forests using generic allometric models. Ecological Applications. 2012;22:572–583.
24. Liu B, Bu W, Zang R. Improved allometric models to estimate the aboveground biomass of younger secondary tropical forests. Global Ecology and Conservation. 2023;41:e02359.
25. Guedes BS, Olsson BA, Sitoe AA, et al. Net primary production in plantations of Pinus taeda and Eucalyptus cloeziana compared with a mountain miombo woodland in Mozambique. Global Ecology and Conservation. 2018;15:e00414.
26. Kumi JA, Kyereh B, Ansong M, et al. Influence of management practices on stand biomass, carbon stocks and soil nutrient variability of teak plantations in a dry semi–deciduous forest in Ghana. Trees, Forests and People. 2021;3:100049.
27. Soaga JA, Adeleye A. Ecological services of a peri–urban recreation centre in Abeokuta, Ogun State, Nigeria. 2022.
28. Babu KN, Mandyam S, Jetty S, et al. Carbon stocks of tree plantations in a Western Ghats landscape, India: influencing factors and management implications. Environmental Monitoring and Assessment. 2023;195(3):404.
29. Chia EL, Kankeu SR, Hubert D. Climate change commitments and agriculture sectoral strategies in Cameroon: Interplay and perspectives. Cogent Environmental Science. 2019;5(1) :1625740.
30. Pirker J, Mosnier A, Nana T, et al. Determining a carbon reference level for a high–forest–low–deforestation country. Forests. 2019;10(12):1095.
31. Fayolle A, Doucet JL, Gillet JF, et al. Tree allometry in Central Africa: Testing the validity of pantropical multi–species allometric equations for estimating biomass and carbon stocks. Forest Ecology and Management. 2013;305:29–37.
32. Kleinschroth F, Healey JR. Impacts of logging roads on tropical forests. Biotropica. 2017;49(5):620–635.
33. Kendie G, Addisu S, Abiyu A. Biomass and soil carbon stocks in different forest types, Northwestern Ethiopia. International Journal of River Basin Management. 2021;19(1):123–129.
34. Cabal C, De Deurwaerder HP, Matesanz S. Field methods to study the spatial root density distribution of individual plants. Plant and Soil. 2021;462:25–43.
35. Tchinmegni FI, Djeukam PSV. Potential of biological invasion for carbon sequestration in a protected area: the case of the Limbe Botanic Garden (LBG) forest, Cameroon. MOJ Eco Environ Sci. 2023;8(2):37–41.
36. Mulatu A, Negash M, Asrat Z. Species–specific allometric models for reducing uncertainty in estimating above ground biomass at Moist Evergreen Afromontane Forest of Ethiopia. Scientific Reports. 2024;14(1):1147.
37. Zhou X, Yang M, Liu Z, et al. Dynamic allometric scaling of tree biomass and size. Nature Plants. 2021;7(1):42–49.
38. Halder NK, Chowdhury MQ, Fuentes D, et al. Intra–specific patterns of δ13C, growth and wood density variation at sites of contrasting precipitation with implications for modelling carbon sequestration of tropical tree species. Agroforestry Systems. 2021;95(8):1429–1443.
39. Khanal S, Nolan RH, Medlyn BE, et al. Disentangling contributions of allometry, species composition and structure to high aboveground biomass density of high–elevation forests. Forest Ecology and Management. 2024;554:121679.
40. Vorster AG, Evangelista PH, Stovall AE, et al. Variability and uncertainty in forest biomass estimates from the tree to landscape scale: the role of allometric equations. Carbon Balance and Management. 2020;15:1–20.
41. Aabeyir R, Adu–Bredu S, Agyare WA, et al. Allometric models for estimating aboveground biomass in the tropical woodlands of Ghana, West Africa. Forest Ecosystems. 2020;7(1):1–23.
42. Dutcă I, Mather R, Ioraș F. Sampling trees to develop allometric biomass models: How does tree selection affect model prediction accuracy and precision? Ecological Indicators. 2020;117:106553.
43. Manolopoulos D, Vasileioris K, Milios E, et al. Allometric models for estimating the height of Robinia pseudoacacia L. in restoration plantations. Land. 2022;11(4):471.
44. Mugasha WA, Mauya EW, Njana AM, et al. Height–diameter allometry for tree species in tanzania mainland. International Journal of Forestry Research. 2019.
45. Cysneiros VC, Pelissari AL, Gaui TD, et al. Modeling of tree height–diameter relationships in the Atlantic Forest: effect of forest type on tree allometry. Canadian Journal of Forest Research. 2020;50(12):1289–1298.
46. Wang Z, Huang X, Li F, et al. Global patterns of allometric model parameters prediction. Scientific Reports. 2023;13(1):1550.
47. Sebrala H, Abich A, Negash M, et al. Tree allometric equations for estimating biomass and volume of Ethiopian forests and establishing a database. Trees, Forests and People. 2022;9:100314.
48. Asigbaase M, Dawoe E, Abugre S, et al. Allometric relationships between stem diameter, height and crown area of associated trees of cocoa agroforests of Ghana. Scientific Reports. 2023;13(1):14897.
49. Tucker C, Brandt M, Hiernaux P, et al. Sub–continental–scale carbon stocks of individual trees in African drylands. Nature. 2023;615(7950):80–86.
50. Djomo AN, Ibrahima A, Saborowski J, et al. Allometric equations for biomass estimations in Cameroon and pan moist tropical equations including biomass data from Africa. Forest Ecology and Management. 2010;260:1873–1885.
51. Duncanson L, Armston J, Disney M, et al. The importance of consistent global forest aboveground biomass product validation. Surveys in geophysics. 2019;40:979–999.
52. Borden KA, Anglaaere LC, Adu–Bredu S, et al. Root biomass variation of cocoa and implications for carbon stocks in agroforestry systems. Agroforestry Systems. 2019;93:369–381.