The process sequence of universal garment hanging system is carried out according to the order of the single task process only. In this paper, Petri nets are used to realize the flexible optimal scheduling of the process in multitask garment production. By considering the competition for equipment resources among process in garment hanging system and the firing rules of transitions, analysis and obtain the process optimal scheduling policy algorithm. The optimal processing sequence and time are obtained by Petri nets simulation. According to the example analysis of the multiple sets of different clothing multitask production, verify the effectiveness of process scheduling in the garment hanging system, and improve the flexible degree of the system.

Keywords: garment hanging system, timed petri net, flexible production, process optimization

S, Seconds; TPPN, Timed Place Petri Nets

With the aggravation of market competition and the improvement of social material level, modern clothing enterprises gradually shift to small batch, multi variety and short cycle production mode.¹ The garment hanging system developed in the 70s Century gradually evolved into the modern transition system with rapid response production technology. It is the centralized application of electromechanical integration technology in garment industry. The cut pieces for processing put on special hangers in the process of production, which transferred into the workstation orderly, and the whole processes completed in hanging state. The flexibility of current garment hanging system is not high although it can quickly replace the production type. Moreover, many problems may appear in multiple clothing productions, such as equipment competitions, assembly line balance, workstation configuration and so on.

People have carried out the research on the optimization of the garment hanging system.^2,3 Yu et al. ⁴ presented the ant colony algorithm to rearrange the locations and workers of workstations without considering the production of different types of clothing. The fitting curve method was used to correct the standard hours of different batch sizes,⁵ which can concluded the man-hour quota of small batch and many varieties production. However, there is no specific control policy of various resources. Mork et al.⁶ provided the genetic algorithm to plan the allocation of job orders in complex and mixed production environment, while there is no study of specific process competition for resources. As a modeling and analysis tool for discrete event systems, Petri nets have been widely used in the control and scheduling of flexible manufacturing systems.^7-9 Su et al.¹⁰ proposed the Timed Place Petri Net model established for a manufacturing system with three processes, and searched for the transition sequence of the model by nested partition algorithm, then optimized the completion time of different batches. However, this method cannot apply in the dynamic scheduling problem. Research by Liu¹¹ and Tian et al.¹² show that the Petri net model based on ant colony optimization can realize the unity of the static modeling and dynamic optimization of the scheduling problem. However, this method is more complicated in multitask processing. Zhou et al.¹³ established the Timed Place Petri Nets model for batch chemical system, combined the model with the optimal scheduling policy, gave the valve control strategies and made the system run efficiently. Zhang et al.¹⁴ applied Petri nets theory in the balance of garment production line, while it did not give specific modeling method and production line balance algorithm.

The limited equipment resources of the production line of garment hanging system make the reasonable arrangement of the process in multitask production become the key problem to improve the flexibility of the system. According to the above literatures, Petri nets possess considerable superiority in the optimal scheduling of flexible manufacturing systems. By considering the correlation between the factors of process and time, this paper adopts the Timed Place Petri Nets as the modeling method on the process optimization problem of garment hanging system. According to the constraint conditions and optimization objectives of the production line, an optimal scheduling algorithm is proposed. Through the analysis of a variety of cases, this method is proved to be effective to solve multitask process optimization problems and can improve the efficiency of the system.

The basic Petri net is a 4-tuple $N=(P,T,F,W)$ , where P and T is finite, nonempty, and disjoint sets. P is a set of places and T is a set of transitions, and $F\subseteq (P\times T)\cup (T\times P)$  is a set of directed arcs with arrows between transitions and places. The element $W:F\to N^{+}$  where $N^{+}$  is the set of positive integers, is a mapping that assigns a weight to each arc, and W is called the weight function of Petri net N. When a graph is used to represent a Petri net, the place is represented by a circle and transition represented by a rectangle. The marking M of a Petri net is a mapping from P to N, $(N,M_0)$ is called the marked Petri net where  is the sum of tokens in all places at initial state of a system, and it is called initial marking of N. Marked Petri net can be expressed as $N=(P,T,F,W,M_0)$ , and the firing rules of transitions are described as follows. A transition $t\in T$  is enabled at the marking M, if and only if $\forall p\in {}^{•}t$ , $M(p)\ge W(p,t)$ . After firing the enabled transitions, the system leaps to another state and yields a new marking $M^{\prime }$ , and $\forall p\in P,M^{\prime }(p)=M(p)-W(p,t)+W(t,p)$ . The definition of TPPN (Timed Place Petri Nets) is $TPPN=(P,T,F,W,M_0,D)$ where D={ $d_1$ , $d_2$  ,…, $d_n$  } is the time delay set of places, $d_i$ is the time delay of $p_i$ , $i\in (1,n)$ . After the fire of a transition t, the corresponding number of tokens moved from input to output places. The tokens put into $p_i$  should hold for time $d_i$  before it becomes available.

TPPN method modeling garment hanging system

Assuming that n tasks $J_1,J_2,\mathrm{...},J_n$  are taken to manufacture n kinds of clothes, the number of process involves in each task is $X_1,X_2,\mathrm{...},X_n$  respectively. Operation of these tasks requires certain resource units, such as ironing table, cup seaming machine, double needle lockstitch sewing machine, cylindrical crimping machine and so on. Otherwise, there is one device for each kind of equipment. Take task $J_i$  as an example, the required cut pieces put on the circular guide rail of the hanging system by computer control, which will send the pieces to workstations according to the order of the process. Operate task $J_i$  requires the cooperation of certain equipments and spend some time executing process, according to its task table, and the finished garments will be send to the unloading station. Due to the concurrent process and resource competition while the system taking multitask productions, different execution sequence of the process will lead to different time to complete the n tasks. It is necessary to consider how to schedule the process to realize that the processing time minimized.

In this work, the Petri net model is completed by two steps. Firstly, establish a Petri net model for a single task. Then, get the TPPN model of the hanging system by connecting subnets via shared device resources. The operation of each process can be described as three stages, the initial, final and processing state. The initial and final state can be considered as two events represented by a set of transitions at the logic level, and the processing state can be considered as the operation state, which represented by a place with time delay. Here, a single task is taken as an example to establish a subsystem model which is shown below.

Given task $J_i$  with $X_i$  processes in a garment hanging system, the TPPN model for garment production of single task is described as $N_{J_i}=(P^{J_i},T^{J_i},F^{J_i},W^{J_i},M_0^{J_i},D^{J_i})$ . In this model, the set of places can be expressed as $P^{J_i}=\{p_s^{J_i},P_{i,j,k},P_{i,j,k}^{\ast },p_f^{J_i},P_k^m\}$ , where places $p_s^{J_i}$  and $p_f^{J_i}$  are initial and final of the task $J_i$  respectively. Operation place $p_{i,j,k}\in P_{i,j,k}$  represents the operation that the process j of the task i by the k-th equipment. The intermediate place  represents a buffer, and resource place $p_{i,j,k}^{\ast }\in P_{i,j,k}^{\ast }$  represents the required equipment. The set of transitions can be expressed as $T^{J_i}=\{T_{i,j,k}^b,T_{i,j,k}^f\}$ where $t_{i,j,k}^b\in T_{i,j,k}^b$  and $t_{i,j,k}^f\in T_{i,j,k}^f$  represent the initial and final events of the operation place $p_{i,j,k}$  respectively. The elements in the set of directed arc $F^{J_i}$  are directed lines between places and transitions, it represent the processing flow of the task. Since each task in garment processing is carried out in a single order, all of the elements in the weight function set $W^{J_i}$  are equal to one. The column vector $M_0^{J_i}={(1,0,\mathrm{...},0)}^T$  denotes that the number of tokens is one in $p_s^{J_i}$  and zero in other places at time zero of the system. The element $d_{i,j,k}\in D^{J_i}$  denotes the time delay of the operation place or the processing time of the operation in terms of garment hanging system. The intermediate and resource place are all places that time delay is zero.

Optimal scheduling policy

The Petri net model is applied to solve the problem of completing the task with the least time. The optimal scheduling algorithm is as follows.

Step 1: Set the priority for the tasks $J_1,J_2,\mathrm{...},J_n$  which are expressed as $L_1,L_2,\mathrm{...},L_n$ . There are $A_n^n$  arrangement methods to the number of n priorities. Therefore, n tasks possess the number of n! priority arrangements.

Step 2: Set no priority for tasks. Select any one as the start point from $J_1,J_2,\mathrm{...},J_n$  respectively. There are a total of n different arrangement methods.

Step 3: Operate the n!+n implementation schemes successively.

Step 4: Search the enabled transitions. If the transition $t_{i,j,k}^b$  possesses the priority, implement Step4.1 to the model, else implement Step4.2.

Step 4.1: If multiple different tasks require the same resource place $p_k^m$  at the same time, the firing sequence of $t_{i,j,k}^b$  is ranked by the priority of the transitions. Record the enabled time ${d^{\prime }}_{i,j,k}$  and firing time ${d^{″}}_{i,j,k}$  for each transition, the waiting time of the transition $t_{i,j,k}^b$  is expressed as ${d^{\prime }}_{i,j}={d^{″}}_{i,j,k}-{d^{\prime }}_{i,j,k}$ .

Step 4.2: If different tasks require the same resource place $p_k^m$  at the same time, the firing sequence of $t_{i,j,k}^b$  is ranked by the sequence of the enabled time ${d^{\prime }}_{i,j,k}$ . Record the value of ${d^{\prime }}_{i,j,k}$  and ${d^{″}}_{i,j,k}$ , then figures out the ${d^{\prime }}_{i,j}$  according to the time difference.

Step 5: Go to Step 4 until all the transitions have fired.

Step 6: The task completion time $d_r={\displaystyle \sum _{j=1}^{X_m}(d_{i,j,k}+{d^{\prime }}_{i,j})}$  where $r\in (1,n!+n)$  represents the r-th kind of implementation scheme, and $X_m$  is the number of the process of the task, which corresponds to the last firing transition.

Step 7: Go to Step 3 until n!+n kinds of implementation schemes are completed.

Step 8: The least time to complete n tasks is expressed as $d=\min (d_1,d_2,\mathrm{...},d_r,\mathrm{...},d_{n!+n})$ . According to the implementation scheme from d, get the sequence and time of the fired transitions in set $T^{J_i}$ .

In order to solve the problem of process scheduling, it is necessary to figure out the sequence and firing time of the start transition $t_{i,j,k}^b$  of each process. Map each transition to the event associated with the process in the system, and get the sequence and firing time of the process of n tasks from the mapping. Then the optimal scheduling policy is obtained. Figure 1 shows the flow chart of optimal process scheduling policy based on TPPN.

Figure 1 Flow chart of optimal scheduling policy of garment hanging system based on TPPN.

Suppose that there are two processing tasks $J_1$  and $J_2$  for the garment hanging system. $J_1$ Contains 13 processes $J_{1,1},J_{1,2},\mathrm{...},J_{1,13}$ , $J_2$  contains 15 processes $J_{2,1},J_{2,2},\mathrm{...},J_{2,15}$ . A total of four equipments are needed,¹⁴ including ironing table, button sewing machine, cup seaming machine and lockstitch sewing machine which are represented as A, B, C and D, respectively. The specific implementation processes of two tasks are shown in Table 1. For the task $J_1$  in Table 1, the Petri net model of the task can be described as $N_{J_1}=(P^{J_1},T^{J_1},F^{J_1},W^{J_1},M_0^{J_1},D^{J_1})$ . Transitions $t_{1,j,k}^b$  and $t_{i,j,k}^f$  represent the initial and final events respectively for each production stage $J_{1,1},J_{1,2},\mathrm{...},J_{1,13}$ , places $p_s^{J_1}$  and $p_f^{J_1}$  denote the initial and final state of $J_1$ , place $p_{i,j,k}$  represents the processing status of the production stages $J_{1,1},J_{1,2},\mathrm{...},J_{1,13}$ , and place $p_{i,j,k}^{\ast }$  is the subsequent buffer place of the $p_{i,j,k}$  (where j = 1, 2 ... 13, k=1, 2, 3, 4). The analogy can be used to reach the meaning of the places and transitions in the task $J_2$  (where j = 1, 2 ... 15, k = 1, 2, 3, 4). For the task $J_2$  in Table 1, the Petri net model of $J_2$  can be described as $N_{J_2}$ =( $P^{J_2}$ , $T^{J_2}$ , $F^{J_2}$ , $W^{J_2}$ , $M_0^{J_2}$ , $D^{J_2}$ ). The transitions $t_{2,j,k}^b$  and $t_{2,j,k}^f$  represent the initial and final events respectively for each production stage $J_{2,1},J_{2,2},\mathrm{...},J_{2,13}$  places $p_s^{J_2}$  and $p_f^{J_2}$  denote the initial and final state of $J_2$ , place $p_{2,j,k}$  represents the processing status of the production stages $J_{2,1},J_{2,2},\mathrm{...},J_{2,13}$ , and place $p_{2,j,k}^{\ast }$  is the subsequent buffer place of the $p_{2,j,k}$ . The Petri net model of $J_1$  is shown in Figure 2.

Figure 2 The Petri net model of production task $J_1$ .

In the same way, the Petri net model of $J_2$  can be obtained by the description of the task $J_2$ . Connect the subnet models of task $J_1$  and $J_2$  via shared resource places $p_1^m,p_2^m,p_3^m,p_4^m$ . The Petri net model of the garment hanging system of two tasks is shown in Figure 3. Set the value of n as 2 in the optimal process scheduling policy. There are four possible implementation schemes for the production. Run the programs of the optimal scheduling policy algorithm in MATLAB environment, the processing time and transitions firing sequence of each scheme can be obtained. Table 2 shows the completion time of the four schemes.

Table 2 shows the implementation scheme, which possesses no priority and $J_1$  start first should be selected. Firing time and sequence of all transitions at the condition of the shortest completion time are shown in Table 3.

In consideration of the correspondence between transitions $t_{i,j,k}^b(t_{i,j,k}^f)$  and the initial (final) event of the production stages in garment hanging system, and the information in Table 3, the optimal process scheduling policy can be obtained from the schedules of production stages. The result is shown in Table 4.

In order to verify the practicability of the method, this paper selects the cases of garment production optimization from Tao¹⁵ and Liu¹⁶, and set multitask processing in Table 5.

Set the value of n as 2, 3, 4, 5, 6 respectively and input process, time and equipment data to the program, the completion time optimized by the algorithm are 902, 1638, 1167, 1543, 1268 seconds respectively. The comparison of consumed time before and after optimization is shown in Figure 4.

The contrast diagram shows that the algorithm presented in this paper is suitable for different styles and multitask process optimization in garment hanging system. Applying the optimal scheduling policy to the garment hanging system can distribute the processing time of each process reasonably, reduce the completion time and improve the efficiency of garment hanging system for small batch and multi variety production.

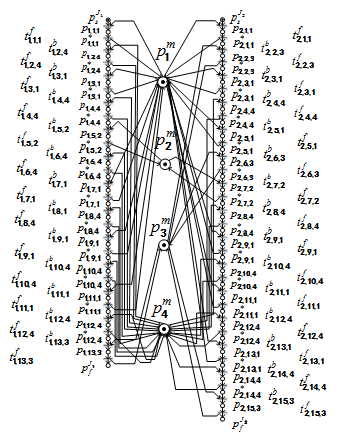
Figure 3 The Petri net model of two tasks.

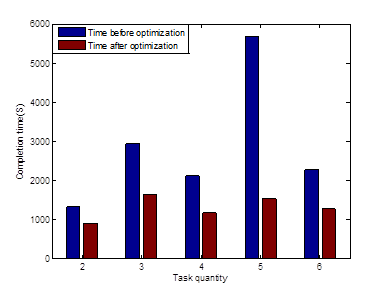
Figure 4 Time comparison of multiple tasks processing.

In this paper, the TPPN is applied to establish the model of the garment hanging system. According to the firing rules of transitions in Petri nets and the processing characteristics of the production line, propose the optimal scheduling algorithm for multitask processing. Simulation experiment shows that the optimal scheduling algorithm, achieves the purpose of high efficiency of garment hanging system in the mode of small batch and multi variety processing. In this study, only the process optimization of multitasks production is considered. Hence, optimizing the personnel allocation at all stages of production according to the operator proficiency in the garment processing will be the next research objective.

The scientific research program is funded by Shaanxi Provincial Education Department under Grant No.16JK1342 and Shaanxi Province under Grant No.2016-GY136, also supported by Xi’an Polytechnic University under Grant No.107090811.

Author declares there is no conflict of interest in publishing the article.

1. Liu WN, Zheng LJ, Sun DH. Application of RFID on multi-varieties and small-batch production management. Computer Engineering & Applications. 2010;46(27):1‒5.
2. Li M, Shi XG. Garment manufacturing process and organization mode oriented for time-based competition. J Textile Research. 2007;28(6):123‒127.
3. Zhao R. The study of the standard working hours formulation of apparel production and assembly line optimization. Master Thesis. 2012;
4. Yu XC, Zeng PF, Zhao R. Garment production assembly line balance based on ant colony algorithm. J Donghua University (natural science). 2014;40(4):456‒460.
5. Ye N, Yan YX. Man-hour quota determination method for garment production of multi-variety in small batch. J Textile Research. 2012;33(6):101‒106.
6. Mork PY, Cheung TY, Wong WK. Intelligent production planning for complex garment manufacturing. J Intelligent Manufacturing. 2013;24(1):133‒145.
7. Hong L, Chao DY. Enumeration of reachable states for arbitrary marked graphs. IET Control Theory & Applications. 2012;6(10):1536‒1543.
8. Hong L, Chao DY. Controllability of weakly dependent control and mixture siphons in S3PR. Inter J System Science. 2013;44(8):1377‒1385.
9. Hong L, Hou YF, Jing JF, et al. Deadlock prevention policy with behavioral optimality or suboptimality achieved by the redundancy identification of constrains and the rearrangement of monitors. Discrete Dynamics in Nature & Society. 2015;(1):1‒15.
10. Su GJ, Wang J, Tian LG. The FMS optimal scheduling based on Petri net mode. Systems Engineering-Theory & Practice. 2014;34(10):2716‒2721.
11. Liu ZL. Research on Parallel Test System Task Scheduling Based on Petri Nets and Ant Colony Algorithm. Master Thesis; 2015.
12. Tian SL, Chen DX, Wang TY. An Asynchronous Parallel Ant Colony Optimization for Flexible Job-Shop Scheduling Problem. Journal of Tianjin University (Science and Technology). 2016;49(9):920‒928.
13. Zhou JZ, Luo JL, Zhang YK. Optimal scheduling and control of batch chemical processes with Petri nets. Control Theory & Application. 2016;33(6):809‒815.
14. Zhang YB, Chen Y. Application of Petri nets in the balance of garment production line. Light and Textile Industry and Technology. 2009;38(1):38‒40.
15. Tao HM. Research on arrangement and Optimization of Apparel sewing Process. Master Thesis; 2005.
16. Liu Y. Clothing mixed-model assembly line balancing and optimization based on Pro Model simulation system. Master Thesis; 2015.