Human activities have involved exposure to vibrations, which are coming from various sources, either from power tools, industrial machines or riding in trains, planes, auto vehicles. The energy gathered from these sources is dissipated in the form of vibrations, some of which being transmitted to people. In this context, the knitted fabrics behaviour at vibrations testing is of special interest, as these materials can be promising for developing the equipment for anti-vibration purpose. The present work aims to present the behaviour of weft spacer and warp spacer knitted fabrics behaviour at dynamic stress. A new method has been used for evaluating the performances of knitted fabrics, through their natural frequencies, caused by one vibration exciter. Fast Fourier Transformation-FFT has been applied and the Spectrum Analyzer application from the LabView software was employed to record the natural frequencies of the system. A critical analysis of the fabrics response to vibrations is performed related to the main parameters of influence.

Keywords: spacer knitted fabrics, vibrations, natural frequencies

The vibration is a mechanical phenomenon which describes the physical energy from a vibrating object, this movement being defined by frequency and amplitude. It has been discovered that the size of working population affected by occupational vibration exposure is high, varying in different countries according to their industrial branches. This regular work in a vibration environment can cause permanent occupational diseases, having also negative influence on the worker’s effectiveness and productivity. One of the economical ways to reduce the risks of vibration injury is to use personal protective equipment to dampen vibrations, creating thus a growing demand of products development in this purpose.¹

In this context, the textile materials as potential vibration absorbers or dampers have attracted the attention of researchers and some results are available in the literature. Special attention has been paid so far to anti-vibration gloves research, considering the high percentage of people working with hand held power tools.² The study about weft knitted spacer fabrics for anti-vibration glove application confirmed their performance properties in this regard and their high potential to substitute PU foam materials.³ Other researchers have focused their interest on the knitted fabrics characterization through their natural frequencies which were determined by employing the free vibrations method.^4-7 The preliminary results confirmed that knitted fabrics can be engineered and exploited as structures with vibration absorption capabilities. Still, limited literature concerning the vibration attenuation capability of the textile materials is available.

Knitted fabrics have found their utilization in the new and rapidly growing trade of technical textiles and composites. The mechanical properties of weft-knitted fabrics are strongly related to fabric structure, yarn properties and fabric direction. Most of the research performed so far concerns the fabric behaviour in static regime. This research main objective is to characterise the dynamic performance of knitted fabrics, which describes the behaviour of one material under very rapid cycling stressing or straining at amplitudes sufficiently small so that rupture does not occur, and in most cases not even much permanent deformation results.⁴ The findings of the author’s previous research are summarised, outlining the main parameters that affect and explain the fabrics behaviour under this type of testing.

Testing method and equipment

The vibration tests of weft and warp knitted fabrics were conducted by using the free vibration method.^4-7 According to the system theory, an elastic system out of the position of stable equilibrium then released, produces free vibrations. In the presence of friction forces, mechanical energy is dissipated and the vibration is damped by a certain number of cycles. Free vibration frequencies depend on the mass, stiffness and damping of the system. They are independent of the initial conditions of the motion or of the system external forces. Therefore, their frequencies are called natural frequency of vibrations. For a given system, they have constant values well defined.⁸

Periodic signals can be written as a countable sum of sinusoidal components whose amplitudes and phases can be easily calculated from these signals, which are Fourier series. Fourier Transformation generalizes the signal decomposition into a sum of sinusoids and non-periodic signals. Fast Fourier Transformation (FFT) allows an easy calculation of the frequency spectrum of a sequence of data. There are several formulas for calculating the Fourier Transformation, which differ by the magnitude of the result, scaling or frequency sign. One of the most commonly used formulas is:

$F\left(\xi \right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(x) e^{-2\pi ix\xi }dx }$ (1)

Under certain conditions the Fourier Transformation can completely recover the original function by applying the inverse Fourier Transformation:

$F\left(x\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(\xi ) e^{2\pi ix\xi }d\xi }$ (2)

From the conceptual argument ξ is a frequency, whereas x is a dimension (temporal or spatial). Fourier Transformation of the function f can be noted symbolically:

$F=F\left\{f\right\}$ (3)

This capacity for reorganization of the Fourier Transformation of frequency information (temporal, spatial or otherwise) is very useful in signal processing of various types, to understanding the properties of many physical systems, to solve equations in other scientific fields theoretical and applied. During vibration, mechanical energy dissipates by friction or other resistance. In the presence of damping, free vibration amplitude decreases over time and to maintain constant amplitude of vibration outside forces should be applied. In general, energy dissipation is called damping. It is produced by internal friction in materials, the friction between the components of one structure, the fluid-structure interactions, radiation and motion in electric or magnetic fields. Structural or hysteretic damping is described by a damping force in phase with velocity, but proportional to the displacement.⁹

In case of knitted fabrics, energy dissipation is determined by relative friction between the yarns and the specific internal friction yarn structure. The friction depends on the nature of yarn, knitted structures, finishing chemical treatments, etc. The dynamic behavior of the knitted fabrics has been studied by analyzing the frequencies that characterize the motion of one attached mass. Frequencies can be measured using an accelerometer attached to this mass.

In this case, dynamic performance of knitted fabrics has been studied by testing the dynamic behaviour of one metallic piece, 391g or 1568g, 30×70×30 mm size, fixed through an adhesive, directly on their surface. The material is fixed also on one heavy plate, with an adhesive, to avoid the relative movements between the piece-knitted fabric-plate. This method allows the measurement of the vibrations of the metallic piece, by using an impact hammer used as an exciter device. The vibrations were produced and measured on three directions: course wise, wale wise and perpendicular on the fabric surface (Figure 1).

Figure 1 Direction of measuring the natural frequencies.⁷

The equipment used as an exciter consists of an impact hammer Piezotronics and vibrations were measured with an accelerometer PCB B52 Piezotronics. The signal is processed with an data acquisition card 6023 National Instruments. In order to determine the natural frequencies of the system, the Fast Fourier Transformation-FFT has been applied and the Spectrum Analyzer application from the LabView 8.2 software ⁹ has been employed (Figure 2).

Figure 2 Spectrum Analyzer application.⁷

The frequencies [Hz] were determined in three directions: coursewise, walewise, and perpendicular on the fabric surface (Figure 3). The frequency at the highest peak represents the natural frequency of the fabric.

Figure 3 Natural frequencies of the spacer weft knitted fabric [Hz].

Selected materials

Weft spacer knitted fabrics: The investigations were carried out on double layers weft knitted fabrics, produced on electronic flat knitting machines of various gauges (E5, E6.2, E8) with outer layers manufactured from PES/EL yarns and PES monofilaments of different diameters as spacer yarns. By considering the different yarn inlay ratio, different spacer yarn diameters, different machine gauge, a number of samples were produced and their characteristics are shown in Figures 4 & 5 and Table 1.

Warp spacer knitted fabrics: Warp knitted fabrics have been produced on double flat needle beds warp knitting machines, DK 506 DPLM and RACOP D4-5, from Liba GmbH, with 4-6 guide bars, threaded in various ratios, in order to create open or closed surfaces on one or both faces. The fabrics are made from PA, PES yarns and monofilaments as spacer yarns, and they can be used for sports shoes, bags, protective vests, gloves, helmets, cushions, mattresses. Their technical characteristics are displayed in Table 2.

Mass per square meter (g/m²) was determined using an electronic balance (KERN ABT 320-4M) and the average of five measured values for each structure was calculated. Fabric thickness has been measured with a thickness Lab Mesdan device, with 0.01 mm resolution, under a compression force of 10 cN/mm², according to the ASTM D1777 - 96(2011)e1 Standard Test Method for Thickness of Textile Materials (Table 3).

Some general aspects can be emphasized from the results obtained after the dynamic testing and these are summarized in the following:

1. Each curve consists of a certain number of waves, the highest peak of the first one in horizontal direction, being the natural frequency of the fabric, measured in [Hz].
2. The level of natural frequency of each material is giving indications about system rigidity, being directly related to it, the higher is the natural frequency, and the higher rigidity is expected.
3. The shape of the curve reveals the capacity of the system to damp the vibrations, the smoother is the shape, the highest is the fabric damping capacity, i.e. the damping capacity of the fabric in course or wale direction (Figures 3A) (Figures 3B) is zlower than in perpendicular direction (Figures 3C).

An ideal weft knitted spacer fabric developed for anti-vibration purposes, should have the capacity of absorb energy efficiently, still having sufficient stiffness to avoid its collapse and an acceptable thickness in order to maintain a sense of touch and dexterity to complete the tasks.³

Weft spacer knitted fabrics

In order to establish the relationship between dynamic behaviour of the spacer fabrics, and their parameters, the frequencies values with different variants of samples were put together in one figure for a facile analysis. Accordingly, results generated by the use of metallic pieces weights of 394g and 1568 g, were separated into Figures 6A) (Figures 6B)respectively.

A closer look to the fabrics dynamic response in connection to their parameters reveals some aspects which can be useful to the fabric engineering process, developed for anti-vibration purposes. A general observation is that, for all samples and for both metallic masses, the frequencies measured perpendicularly to the surface have the highest values. This can be justified in relation to the cross section of the fabrics, determined by their thickness and by the monofilament yarns used as spacers.

The number of spacer yarns per needle inside the structure is influencing fabric behavior. Studying the pair of samples S5-S6, one can notice that the main difference between them is the number of monofilaments threaded to the needles, 1:5, double pile yarn inlay and 1:5 single pile inlays, respectively. So, in case of the 1568 g seismic mass (Figures 4B) the S5 sample responded and attenuated better the vibrations, due to the double number of spacer yarns, which act as a linear spring, deforming the loops under impact and hence creating a better vibrations absorption. S4-S5 is another example, the double number of spacer yarns per needle in S5 structure, gives it a higher stability after the washing treatment and less movement of the yarns inside the fabric. Therefore, the number of contact points between the layers is lower and fabric rigidity as well (see S4, from (Figures 4A)(Figures 4B).

Figure 4 Structure section 1:3 pile yarn inlay.⁷

The finishing treatment, respectively the washing after knitting at 90C, modifies the fabric reaction to test. S3-S4 fabrics are an example relevant, S4 was washed and it suffered shrinkage after washing due to the elastic yarns, gathering a higher thickness, a higher number of contact points in the cross section and consequently an increased rigidity under the higher seismic mass (Figures 6B).

Figure 5 Structure section 1:5 pile yarn inlay.⁷

Figure 6 Natural frequencies of the spacer weft knitted fabrics.⁷

Spacer yarn diameter has a relevant influence on the fabric behaviour. Examining the pair S4-S7, it is noticeable that even a small diameter difference of 0.02 mm for S4 determines a higher fabric square mass, consequently higher fabric rigidity, demonstrated by the higher values of frequencies in both seismic mass testing, compared to S7 fabric.

The inlay yarns ratio per needle is another factor of influence, considering S5-S6 fabrics. S6 has a higher number of contacts due to the 1:3 double yarn ratios, thus increased fabric rigidity at low seismic mass and a similar behaviour at higher seismic mass. Besides, the yarn diameter confirmed again its influence, having a higher value for S6 fabric, giving thus its higher rigidity.

Warp spacer knitted fabrics

Due to the low number of available samples, and not experimentally planned, it was difficult to demonstrate clearly which effect has fabric thickness on this type of testing. Still, from Table 2 and Figures 4, it can be observed that some fabrics exhibit close values of the thickness and accordingly, close values of the recorded frequencies. By analyzing the fabrics, it is noticeable that fabrics S10-S11, S1-S9, S2-S7, S4-S5, S12-S13 having similar values of their thickness, prove a comparable behaviour in terms of the recorded frequencies (Figures 7). A close view of the pair of structures S10-S11 and S2-S7, allows some preliminary conclusions to be drawn, concerning the factors that might have an influence on their behaviour. The pair of samples has similar lapping, comparable surface aspect and almost the same thickness, but different level of frequencies with a significant amount, from 26-28 Hz (S10-S11), to 68-73 Hz (S2-S7). The conclusion is that their thickness has not a major influence, but other factors.

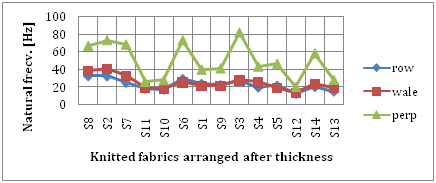
Figure 7 Fabrics natural frequency according to the thickness.⁵

Analysing the fabrics characteristics, the situation can be explained by their technological and structural differences, such as: the different number of the guide bars for the spacer yarns, which in case of S10-S11 is one and for S2-S7 is two, generating thus a higher number of spacer yarns in the unit area and a higher frequency level, translated into a higher fabric rigidity. The spacer yarns threading for S10-S11 is under a certain ration, meanwhile the S2-S7 have two fully threaded guide bars to connect the layers. Also, S10-S11 have a lower number of guide bars to produce the fabrics (3 and 4) and the group S2-S7 is made of 6 guide bars, 4 of them fully threaded. Another factor that affects and contributes to the lower rigidity of the fabrics S10-S11 is the finishing process, the samples being shared on the back side and some of the underlaps partially destroyed. Close values of frequencies have been obtained by samples S1-S9 and S4-S5, despite of their different thickness and this fact has to do with the spacer yarn which has same fineness (dtex 33 f1 Monofil PES) and threading for all samples.

The highest peak of the frequency on perpendicular direction (82,3Hz) has been registered by the fabric S3, where the spacer yarn of PES 53 dtex f1 monofilament is fed by two fully threaded guide bars, both having high yarn consumptions, bar 3-7230 [mm/rack] and bar 4-9150 [mm/rack]. This yarn and threading arrangement determines increased fabric rigidity, confirmed by the high level of the frequency. It is followed by the fabric S6 (73,6Hz) where the spacer yarn is PA 22 dtex f1 monofil, fully threaded in the guide bars 3 and 4, with a yarn run-in of 5400 [mm/rack]. It can be assumed that the spacer yarn type (PA or PES), at the same threading plays a significant role in the fabric response.

In order to complete the fabric's characterization, the displacements of the attached mass have been measured. It has been determined with some inductive displacement transducers, connected to a data acquisition system, Spider 8 from Höttinger Baldwin Messtechnik and the data were processed with Catman Easy data acquisition software. Displacement amplitude measurement allows a view of how the vibration damping is performed by various fabrics. It has been established that the maximum values of the displacements are of max. 1 mm, regular values being approx. of 0.5-0.6 mm. The metallic mass displacement until the movement stop is of approx. 0.1 sec (Figures 8).

Figure 8 Mass displacement on perpendicular direction.⁵

The preliminary conclusions of the research performed can be summarized as follows:

1. The different values of frequencies between fabrics can be attributed to the spacer monofilament yarns diameter, the patterning of the spacer yarns and the threading of monofilaments.
2. The differences found between measured values of the frequencies course and wale wise, with metallic mass weight changing from 391g (Figures 6A) to 1568g (Figures 6B) can be explained by the shrinkage of the spacer fabric when it is removed from the knitting machine, so the surface loops in course direction are closer to each other, modifying the contact surface with the metallic mass and the number of wales per testing unit.
3. The comparable behaviour of the fabrics on the two directions for a small seismic mass weight can be attributed to the vibration mechanism, which in this case does not involve any movement or distribution of the yarn inside the structure.
4. The most significant values of the fabrics natural frequencies were recorded on perpendicular testing direction, demonstrating the system high rigidity and its capability of damping well the vibrations, fact confirmed also by the shape of the frequency curve, with low peaks and smooth profile.
5. Finishing process by its agent’s action, proved a certain influence on the higher natural frequencies values of the tested fabrics. The consolidation process of yarn contacts is taking place, determining the shrinkage of the fabrics, a lower yarns friction inside the fabric and thus an increased rigidity of the structure.

The free vibration method has been used for the dynamic testing of weft and warp spacer knitted fabrics, in order to investigate their potential to attenuate the vibration effect, mostly in the environments where people are affected by the working conditions.

In order to improve the vibration reduction property, there is need to design and test more knitting structures and materials, due to the fact that spacer knitted fabrics properties are influenced by many different construction parameters. Both, weft and warp fabrics demonstrate a good potential for anti-vibration materials and for further research.

An in-depth investigation is recommended to carry out, on yarns properties, modeling of the internal structure of the fabrics and finishing treatment of the knitted fabrics. If the spacer knitted fabrics are effective to reduce vibration in a wide frequency range, it may conduct to various applications and create a new direction for products development.

The authors would like to acknowledge the support of the Technical University of Dresden, Institute of Textile Machinery and High Performance Material Technology (ITM) for providing the weft spacer knitted fabrics for testing and the Company Liba GmbH, Naila, Germany for providing the warp spacer fabrics for study.

This research has been published originally in the Books of Proceedings of AUTEX 2013 and AUTEX 2014 conferences.

Author declares there is no conflict of interest in publishing the article.

1. Mansfield N. Human response to vibration. New York Washington: Taylor & Francis e-Library; 2005.
2. Liu Y, HU H. Vibration Isolation Performance of Warp-knitted Spacer Fabrics. 2013.
3. Sum NW. Development of anti-vibration glove with weft knitted spacer fabrics. BA thesis, Institute of Textiles&Clothing, The Hong Kong Polytechnic University, Hong Kong. 2013.
4. Seghedin NE, Blaga M, Ciobanu R. Weft knitted fabrics behaviour under dynamic testing. 12th World Textile Conference AUTEX. Zadar, Croatia, 2012. p. 455‒461.
5. Blaga M, Seghedin NE, Ciobanu AR. Dinamic testing of the warp knitted spacer fabrics. 13th Autex World Textile Conference. Dresden, Germany; 2013.
6. Blaga M, Seghedin NE, Ciobanu AR. Warp knitted fabrics behaviour under dynamic testing. Industria textilă. 2013;64(6):334‒341.
7. Blaga M, Seghedin NE, Ciobanu AR. Weft knitted spacer fabrics response to vibrations. 14th AUTEX World Textile Conference. Bursa, Turkey; 2014.
8. Rades M. Vibratii mecanice (Mechanical vibrations), Bucharest: Printech publishing house; 2008.
9. Goldman S. Vibration Spectrum Analysis. A Practical Approach. 2nd ed. New York: Industrial Press; 1999. p. 331.