The main aim of the work is to analyse the airflow character and fluid variables of the air nozzle of Jetring spinning system computationally. In numerical simulation, ANSYS 12.1 package program and Fluid Flow (CFX) analysis method was used. Our numerical analysis differs from the literature regarding to three contributing causes. One of them is the type of the solution algorithm. Standard and also modified k-ε turbulent models were widely used for the numerical analyses of the nozzle in which pressurized air is fed. In our study, Shear Stress Turbulent (SST) model is preferred regarding to the solution duration and also solution stability. The second contributing cause is the boundary condition and solution validation. Mass flow values of the air in the nozzle were measured by electronic mass flow meter and the values were compared with the calculated values obtained by the numerical analysis. The last cause is the yarn component of the Jetring system. Contrary to assumption of the insignificant effect of the yarn on to the airflow in the literature, the yarn was modeled and the area from where the yarn is passing was included to the numerical analysis. Consequently, we determined the calculated and measured values are almost compatible. It was observed different types of airflow in mainly three different parts of the nozzle with different air velocities and pressure values.

Keywords: nozzle, jetring, CFD, airflow, fluid flow, numerical analysis

There are two fundamental approaches to design and analysis of the engineering systems that involve fluid flow: experimentation and calculation. The former typically requires the construction of the models that are tested, while the latter is based on the solution of differential equations, either analytically or computationally. The solution of the equations of fluid flow through the computer is introduced as computational fluid dynamics (CFD). For example, lift, drag, pressure drop, or power can be obtained experimentally while computational fluid dynamics is required for the details about the flow field, such as shear stresses, velocity and pressure profiles, and flow streamlines Cengel & Cimbala.¹ In fact, both methods are complementing each other and therefore they cannot be thought one by one. Experimental data are often used to validate CFD solutions by matching the quantities obtained computationally and experimentally. CFD is then employed to reduce the required amount of experimental testing and thereby shortening the design cycle.

CFD are being used increasingly to describe highly complex fluid flow processes, shock/boundary-layer interactions, turbulent reacting flows, and multiphase flows Aeschliman & Oberkampf.² The main commercially available CFD packages on the market are FLUENT, CFX, STAR CD, FLOW 3D and PHOENIX Fokeer.³ In this study, airflow inside the nozzle and also on to the yarn passing through the nozzle of the Jetring spinning system was simulated using a Fluid Flow (CFX) analysis method of ANSYS 12.1 package and thereby nozzle performance was determined.

Jetring is a spinning system based on the placement of an air nozzle on to conventional ring spinning system. As from 1990s, there have been the attempts to associate the conventional ring and air-jet spinning systems and thus to improve the properties of conventional ring spun yarns. Jetring spinning system consists of three components: nozzle, pressurized air and the yarn. Therefore, the researchers mainly analysed the effect of air pressure level and the structural parameters of the nozzle on airflow character and also the yarn quality either experimentally or computationally. In numerical analyses, Zeng & Yu⁴ used PHOENICS while Patnaik et al.^5,6 Rengasamy et al.^7,8 realized the simulations by fluent package programs and they all used standard k-ε turbulent model as a solution algorithm. On the other hand, Guo et al.^9-11 worked on the simulation of the nozzle used in air-jet spinning system. Standard k-ε turbulent model is widely preferred for the turbulent model in the engineering application and hence all these numerical analyses were realized by standard or modified k-ε model. In Murata vortex spinning, which is considered as a modification of air-jet spinning, the flow field inside the nozzle was also simulated by realized k-ε model Zou et al.¹² Pei & Yu^13,14 Nevertheless, k-ε model does not perform very well for the flows with boundary layer separation, sudden changes in swirling and rotating flows and flows over the curved surfaces Guo et al.^9-11 However, Shear Stress Transport (SST) model accounts for the transport of the turbulent shear stress and gives highly accurate predictions of the onset and the amount of the flow separation under adverse pressure gradients.¹⁵ On the other hand, in literature, it was assumed that the yarn passing from the nozzle can not affect the flow inside the nozzle and therefore the yarn was not modeled during simulation. Base on above reasons, the present work aimed to simulate the airflow in the nozzle and also on to the yarn using the Shear Stress Transport (SST) turbulent model.

CFD problems comprise of four main components and this study is realized the solution following these components. The components are:

1. Constituting of the nozzle geometry
2. Intersecting the geometry into the cells and grid generation
3. Setting up a physical model and solving it
4. Post-processing of the computed data

Nozzle configuration

In the study, each inlet region of the nozzle configuration was firstly created in ANSYS Workbench as a fluid. The nozzle used in present work has a cylindrical cross section and consists of main whole (1), injectors (2), twisting chamber (3) and nozzle outlet (4) (Figure 1). Main hole lies starting from the nozzle inlet to nozzle outlet and the nozzle has a diameter of 2.0, 2.5 and 3.0 mm. Injectors are positioned at certain angles with respect to the nozzle axis and so they lie tangentially. The vertical angles of the injectors (θ) are 15˚, 30˚ and 45˚. Air enters with these mentioned angles to the main hole. Each nozzle has four injectors and their diameter varies the range between 0.5 mm and 1.5 mm range.

Figure 1 Nozzle geometry.

Compressed air is supplied from the compressor to the nozzles through the pipe (Figure 2). The compressed air coming from the compressor passes from the opening (5) and it is transferred into the nozzle by means of the injectors. Air pressure was kept at 0.5 MPa at the compressor outside.

Nozzles used in the study are different from each other regarding with the nozzle structural parameters such as injector angle, main hole and injector diameters (Figure 3). In the analysis, one of the structural parameters is changed when the others keep constant.

Figure 2 Transferring the compressed air into the nozzle.

Figure 3 Nozzle structural parameters.

It is assumed that the cross-sectional area of the yarn is about 1/100th to that of the main hole of the nozzle and the yarn occupies a small area in the nozzle. Hence, the flow inside the nozzle affects the yarn, but not vice versa Patnaik et al.⁶ Rengasamy et al.⁸ Therefore, the yarn was not modeled in the numerical analyses concerning with Jetring or air-jet spinning systems. Present work includes the area from where the yarn is passing and studies the flow field around the yarn even if the effect of the yarn is accepted as insignificant (Figure 4). We believe that the yarn is one of the most important components of these spinning systems. Additionally, it was given a speed which is equal to production speed of spinning machine to the yarn (approximately 0.2 m/s).

Figure 4 Projections of the yarn in the nozzle and nozzle injectors.

Grid generation and meshing procedure

Following to the geometry, the first step in a CFD solution is the generation of a grid that defines the cells on which flow variables (velocity, pressure, etc.) are calculated throughout the computational domain Cengel & Cimbala.¹ Therefore, the design being studied was divided into many small elements called as the cells (Figure 5). Each cell can be thought as a tiny control volume in which discredited versions of the conservation equations are solved.

Figure 5 Grid structure.

The quality of a CFD solution is highly dependent on the quality of the grid. During the grid generation, sharp-pointed angles are occurred due to the intersections of the injectors and twisting chamber. Hence, it is difficult to obtain a regular mesh in the entire geometry. On the other hand, injectors are one of the most important nozzle structural parameters concerning with the fluid flow and therefore it was given importance to generate a regular grid structure in this section. We followed a strategy applying the automatic mesh option to the section between the injectors and yarn entering zone while using a structured mesh to the section of nozzle exit (Figure 5).

The mesh was built with the finite volumes or grid points varying between 200.000 and 9.000.000. For each nozzle type, number of grid points was increased to check the independence of the solutions on the grid points. However, solution procedure takes more time such as 2-3 days as the volume number reaches 9.000.000. When the solutions having lower volume density were compared with the solutions comprising higher volume number, it was determined that the mesh employed produces satisfactory results and further refinements of the grid or volume number will not be beneficial. And the solution procedure was about 3-4 hours for approximately 400.000 elements. Considering the computational effort and time consuming, it is better to employ the mesh cases having lower finite volumes.

Physical model and its solution

ANSYS Fluid Flow (CFX) package uses a Finite Volume (FV) method for airflow simulation inside the nozzle. A finite number of continuous control volumes constitute the solution domain, and the integral form of conservation equations is applied to the each control volume Rengasamy et al.⁸

In nature, every fluid flow display turbulent flow character and the airflow inside the nozzle is also turbulent. Any fluid flow including turbulent flow properties is governed by following equations and these are mass conservation (continuity equation), momentum conservation, energy conservation, and ideal gas equation.

The series of the governing equations are solved according to the boundary conditions which describes the physical properties of the fluid flow.

Solution algorithm: turbulence models

There are still many questions about the modelling and properties of turbulent flows. Also a universal turbulence model is not available yet. Therefore, many models have been developed to calculate the effect of turbulent flow. In present work, it is used “Shear Stress Transport (SST)” turbulent model, which is one of the Reynolds stress models, as a solution algorithm.

In general, Navier-Stokes equations describe both laminar and also turbulent flows without the need of additional information. Turbulence consists of fluctuations in the flow field depending on time and space. It is a complex process, mainly because it is three dimensional, unsteady and comprising many scales. Thus, it is required to use the averaged of fluctuating physical quantities in Navier-Stokes equations. Reynolds averaging process leads to arise additional terms. One of the most important terms is $-\rho {\mu }^{\prime }{{\overline{\mu }}^{\prime }}_{ij}$  and it is called as Reynolds Stress Tensor. In the approaches based on Eddy viscosity model, Reynolds Stress Tensor $(-\rho {\overline{{\mu }^{\prime }}}_i{\overline{{\mu }^{\prime }}}_j)$  is related to the mean velocity gradients and eddy (turbulent) viscosity by the gradient diffusion hypothesis in a manner analogue to the relationship between the stress and strain tensors. Two-equation turbulent models developed basing on mentioned relations have been using in many engineering problems successfully. By far the most popular turbulence models utilized today for flow transfer calculations are the two-equation eddy viscosity models: k-ε, k-ω, BSL and SST. In particular, two-equation k-ε model is unarguably the most widely used and validated model employed for turbulent fluid dynamics to date Garg et al.¹⁶ Dhinsa et al.¹⁷ The extensive use of the model has highlighted both its robustness and low computational expense Haque et al.¹⁸ Standard k-ε turbulent models were also widely used for the numerical analyses of the nozzle in which pressurized air is fed Patnaik et al.⁶ Guo & Yu ¹⁹ Guo & Yu⁹ Rengasamy et al.⁸ Although k-ε turbulent model produces the reasonable results, the model does not perform very well for the flows at the boundary layer separation, sudden changes in swirling and rotating flows and flows over the curved surfaces Guo et al.^9-11 Wilcox²⁰ suggested another model (k-ω) based on the improvement of standard k-ε turbulence model. The inadequacies in k-ε, k-ω and BSL models lead Menter to formulation the Shear-Stress Transport (SST) turbulence model. Shear Stress Transport (SST) model encompasses both the k-ε and the k-ω models, with the original k-ω model of Wilcox²⁰ activated in the near-wall region and the standard k-ε model activated in the outer wake region and in free shear layers Dhinsa et al.¹⁷ Bartosiewicz et al.²¹ Haque et al.¹⁸ Shear Stress Transport (SST) model accounts for the transport of the turbulent shear stress and gives highly accurate predictions of the onset and the amount of the flow separation under adverse pressure gradients.¹⁵ Following Menter,²² the equations for the SST model can be written as:

$\frac{D\left(\rho k\right)}{Dt}={\tau }_{ij}\frac{\partial u_i}{\partial x_j}-\beta *\rho \omega k+\frac{\partial }{\partial x_j}\left[\left(\mu +{\sigma }_k\mu \right)\frac{\partial k}{\partial x_j}\right]$ (1)

$\frac{D\left(\rho \omega \right)}{Dt}=\frac{\gamma }{vt}{\tau }_{ij}\frac{\partial u_i}{\partial x_j}-\beta *\beta \rho {\omega }_2+\frac{\partial }{\partial x_j}\left[\left(\mu +{\sigma }_{\omega }{\mu }_t\right)\frac{\partial \omega }{\partial x_j}\right]+2\rho {\left(1-F\right)}_1{\sigma }_{{\omega }_2}\frac{1}{\omega }\frac{\partial k}{\partial x_j}\frac{\partial \omega }{\partial x_j}$ (2)

Where shear stres is given by

${\tau }_{ij}={\mu }_t\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}-\frac{2}{3}\frac{\partial u_k}{\partial x_k}{\delta }_{ij}\right)-\frac{2}{3}\rho k{\delta }_{ij}$ (3)

${\delta }_{ij}$  Is the Kroneckar delta. Note that the production term in Eqs. (1) Or (2) can be written as

${\tau }_{ij}=\frac{\partial u_i}{\partial x_j}{\mu }_t\left(S_{ij}^2-\frac{2}{3}{\left(\frac{\partial u_k}{\partial x_k}\right)}^2\right)-\frac{2}{3}\rho k\frac{\partial u_k}{\partial x_k}$ (4)

Where the strain rate tensor is given by

$S_{ij}=\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}$ (5)

If φ1 represents any constant in the original k-ω model (σk1, ….), and φ2 any constant in the transformed k-ε model (σk2, ….), then φ, the corresponding constant of the new model given by Eqs (1) and (2) is

$\varphi =F_1{\varphi }_1+\left(1-F_1\right){\varphi }_2$ (6)

$F_1=tanh\left(ar{g}_1{}^4\right)$ (7)

${\arg }_1=\min \left[\max \left(\frac{\sqrt{k}}{0.09\omega y},\frac{500v}{v^2\omega }\right)\frac{4\rho {\sigma }_{{\omega }_2}}{C{D}_{k\omega }{y}^2}\right]$ (8)

$C{D}_{k\omega }=\max \left(2\rho {\sigma }_{{\omega }_2}\frac{1}{\omega }\frac{\partial k}{\partial x_j}\frac{\partial \omega }{\partial x_j},10-20\right)$ (9)

For the SST model, the various constants are

${\sigma }_{k_1}=0.85$ , ${\sigma }_{{\omega }_1}=0.5$ , ${\beta }_1=0.075$ , ${\alpha }_1=0.031$ , $\beta *=0.09$ , $k=0.41$ , ${\gamma }_1=\frac{{\beta }_1}{\beta *}-{\sigma }_{{\omega }_1}{k}^2/\sqrt{\beta *}$ , ${\sigma }_{k_2}=1.0$ , ${\sigma }_{{\omega }_2}=0.856$ , ${\beta }_2=0.0828$ , ${\gamma }_2=\frac{{\beta }_2}{\beta *}-{\sigma }_{{\omega }_2}{k}^2/\sqrt{\beta *}$ (9)

$v_t=\frac{{\alpha }_{1}k}{\max \left({\alpha }_1\omega ,\Omega F_2\right)}$ (10)

Where F2 is given by

$F_2=\tanh {\left(\arg \right)}^2$ , ${\arg }_2=\max \left(2\frac{\sqrt{k}}{0.09\omega y},\frac{500v}{y^2\omega }\right)$ (11)

Where

CD: specific heat at constant pressure

F1, F2: constants

k: turbulence kinetic energy

ℓ: turbulence length scale

Pr: Prandtl number

k: recovery factor=Pr1/3 (for turbulent flow)

s: distance from the leading edge along the pressure or suction surface

S: strain rate

u: velocity

x, y, z: cartesian coordinate system with origin at the geometrical stagnation point, and z in the spanwise direction

y+: distance in wall coordinates (=y ν* / ν)

α: thermal diffusivity

α1: constant

β, β*: constants

ε: turbulence dissipation rate

γ: constant

κ: von Karman constant

μ: viscosity

ѵ: kinematic viscosity

ρ: density

σ: constant

τ: shear stress

ω: spesific turbulence dissipation rate (=ε/k)

Ω: absolute value of vorticity

The near wall treatment is of equal important in practical industrial CFD simulations as the formulation of the turbulence model itself. The basic idea behind scalable wall function approach used in ANSYS CFX is then to limit the computed y⁺ value used in the logarithmic formulation from falling below 11.06, which is the value assumed for the intersection between the logarithmic and the linear near-wall profile Codorin et al.²³ SST model requires the distance of a node to the nearest wall for performing the blending between k-e and k-w models. For details about wall function approach, ANSYS CFX help file can be given as reference source.

In this study, different turbulent models are performed. Consequently, both solution duration and also solution stability lead to use SST model and SST model is preferred. On the other hand, mass flow values measured by electronic mass flow meter are compared with the calculated values by the numerical analysis and it was determined that calculated values converge to the measured values.

Boundary conditions

Appropriate boundary conditions are required in order to obtain an accurate CFD solution. At the inflow or outflow cases, either velocity or pressure conditions are specified at the boundaries which fluid enters the computational domain or leaves the domain. The present work uses the pressure condition as a boundary condition because we have not any measured data about the air velocity for any nozzle geometry. For each nozzle type, the air pressure at the nozzle inlet was measured in terms of the electronic mass flow meter (Figure 6). In the measurements, a mass flow meter of Alicat Scientific firm is used and placed between the compressor and nozzle opening (Figure 7). Therefore, we specify the total pressure at the nozzle inlet in which the flow is coming into the computational domain from the compressor.

On the other hand, when the pressurized air is leaving from the compressor, its level is known in terms of the readings from the manometer. Following to the measurements, it was determined that the pressure values obtained by mass flow meter are different from the readings on the manometer. In another words, the pressure values at the compressor outlet are not same at the nozzle inlet. We believe that this difference is resulting from the nozzle geometry. Therefore, the pressure levels were measured at the nozzle inlet by the mass flow meter and they were used in numerical analyses (Figure 8) (Figure 9).

Figure 6 Mass flow measurements in terms of electronic mass flow meter.

Figure 7 Measurement flow diagram.

Figure 8 The airflow at the nozzle inlet and outlet.

The experimental structure used in present work consists of the yarn, nozzle inlet or main hole, injectors and nozzle outlet. Therefore, there are a few pressure inlets and outlets in the computational domain. The external boundaries of the nozzle geometry are called as “wall or plane”.

Internal boundary conditions: The direction of the airflow at the nozzle inlet varies depending on the nozzle configuration and so it is not possible to specify accurately at the beginning of the analysis. Therefore, nozzle inlet or main hole was defined as “opening” and the cases of air coming in or leaving was being the optional depending on the main flow conditions in the nozzle. At the nozzle inlet or main hole, the air pressure was the atmospheric pressure conditions.

Figure 9 Converging of the solution.

External boundary conditions: Atmospheric pressure was assumed at the nozzle outlet.

Wall boundary conditions: Non-slip boundary condition was applied to the nozzle walls. Therefore, the flow between the air and nozzle wall was considered non-slip and having any velocity.

Yarn boundary condition: Boundary condition for the yarn was taken as non-slip. However, it was given the equal speed to the production speed of conventional ring spinning machine (about 0.2 m/s).

Fluid type and properties

The type of fluid such as water, air, gasoline, etc. and fluid properties such as temperature, density, viscosity, etc. affect the fluid flow. The fluid type in this work was the compressible airflow and fluid properties were specified as ideal gas.

Initial conditions

In a CFD solution process, the conservative equations are solved iteratively for each cell. Sometimes hundreds or even thousands of iterations are required to converge on a final solution and thus the residuals may decrease by several orders of magnitude. In the work, iteration number was taken five as a minimum value and 300 as a maximum. Depending on the converging condition of the solution, iteration was performed over 300. Sensitivity of the solution was set at 10^-5. In addition, one point is defined to check the solution converging and the quantities such as pressure, velocity etc. were monitored. As it is seen in Figure 9, when the sensitivity of mass, momentum and energy equations shown by different colours reaches 10×10^-6, iteration loop is almost equal to 300 and the deviations in the solution decreases and also the defined point is settled down to the constant values (Figure 10).

Post-processing of the computed data

To check the accuracy of the solution, the computed mass flow values were compared with the measured mass flow data for each nozzle type. Depending on the difference in the both values, it was rearranged the mesh structure of the geometry and iteration loop to get the best solution.

Figure 10 Control point and the variations in the solution for this point.

Once the solution was converged, flow field variables such as air velocity and pressure were obtained. In the work, these variables associated with the attitudes of fluid flow were analysed under three parts. They are:

1. Firstly, it was studied the fluid flow coming from the injectors and ending at the nozzle outlet. This attitude of the fluid directly represents the initial activity of the pressurized air in the nozzle.
2. Then, we investigated the fluid flow behavior starting to grow up at the nozzle inlet and ending at the nozzle outlet. This flow type is affected from the airflow participating from the injectors.
3. Last of all, it was analysed the airflow either around the yarn or at the cylindrical area close to the yarn surface.

Validation of the solution

To insure the solutions, mass flow values of the pressurized air sent into the nozzle were measured by electronic mass flow meter and compared with the calculated values by the numerical analysis. It was determined that the calculated and measured values are almost compatible. However, the values are not completely the same as we desired. There are differences in the values and the differences are reaching up to 2-3 times. As it is seen in Figure 11, the regression coefficient representing the relation between the computed and measured data is 62.15%. Although this coefficient is satisfying, it is not as much as we desire. It is believed that the differences in the data may result from the nozzle configuration associated with the air density value.

When the mass flow values are calculating on the electronic mass flow meter, the air density is assumed as constant and equal to 1.18 kg/m³. According to the CFD analysis, the air density value changes along the nozzle length in all nozzle types and its value is about 1.9-2.14 kg/m³ at the injectors, 1.16-1.3 kg/m³ at the nozzle inlet while 1.09-1.25 kg/m³ at the nozzle outlet (Figure 12). These air density values and even the average of these values are considerably higher than the value taken into consideration in the measurements which is equal to 1.18 kg/m³ and this causes disaccording between the measured and computed data.

Figure 11 The relation between the mass flow values.

(a)                            (b)

(c)

Figure 12 Air density values of the nozzles having 15˚ (a), 30˚ (b) and 45˚ (c) injector angles.

As it was also mentioned in the literature, the analyses of ANSYS Fluid Flow (CFX) indicate that pressurized air swirls along the nozzle and an air vortex is occurred in the nozzle. In fact, there are two types of swirling airflow having different rotating directions in upstream and downstream of the nozzle.

On the other hand, it is not possible to explain the airflow characters in the nozzle with a single structure. Actually, different types of airflow arise with different air velocities and characters in mainly three different parts of the nozzle. One of them is the airflow sent from the injectors and moving on the nozzle walls. Another one is coming from the nozzle inlet and under the effect of airflow getting from the injectors. The last one is the airflow around the yarn. These mentioned fluid behaviors lead to the air displaying different flow attitudes at the nozzle injectors, main hole and nozzle outlet associated with different airflow properties. In addition, flow field variables of the air velocity and pressure vary at the position where the injectors are opened into the main hole, nozzle inlet and also nozzle outlet. Therefore, all airflow structures and variables should be analysed for each nozzle type.

The air pressure results

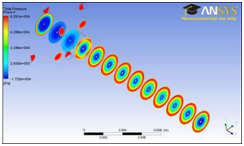
When the changes in the air pressure values are studied, it was found that a suction effect or negative air pressure arises at the nozzle inlet (Figure 13). Following to the nozzle inlet, air pressure increases with the pressurized air sent from the injectors and its value reaches to maximum level at the injector region. Along the nozzle length, air pressure value is the lowest at the centre while it is the highest close to the walls. From axis to the wall, air pressure increases to a certain point. The rule of air pressure distribution is the same for all injector angles. When the graphs of the air pressure are analysed, it was observed that air pressure values sometimes fall under the atmospheric air pressure level (101325 Pa) and this case also verifies the suction effect.

(a)                            (b)

(c)

Figure 13 The changes in air pressure values of the nozzles having 15˚ (a), 30˚ (b) and 45˚ (c) injector angles.

At the nozzle outlet, the air pressure values inside the nozzle are different from that of the exterior pressure value and thus the suction effect is created intensively at the nozzle centre. In particular, the air inside the nozzle sucks the air from the outside into the nozzle due to lower air pressure in the nozzle.

In Figure 14, it is given the air pressure distribution of the airflow along the nozzle length for all injector angles. Plane 1 and plane 2 represents the nozzle inlet while plane 3 and plane 4 shows the injector region of the nozzle. Lastly, plane 9 and plane 13 indicates the nozzle outlet. In the profiles, it is easy to see the suction effect at the nozzle inlet and outlet, and also higher air pressure at the nozzle walls.

Figure 14 Air pressure profiles for the different injector angles.

Suction effect at the upstream of the nozzle is occupying smaller area in 15˚ comparing with the nozzle having 45˚ (Figure 13). In comparison to the angle of 45˚, 15˚ is more straight angle and this causes the air acting on the nozzle wall. Similar to the findings in the literature, the suction is observed intensively at the upstream where is between the nozzle inlet and injectors for the 45˚ injector angle Oxenham & Basu²⁴ Zeng & Yu²⁵ Guo & Yu.¹⁰ As the injector angle increases, the air pressure value at the nozzle centre and walls rise.

Regarding to the main whole diameter, in 2.0 mm, the pressurized air coming from the injectors entirely fills the interior of the nozzle instead of the rubbing to the nozzle walls. Therefore, the suction loses its effect at the nozzle inlet and centre, and hence higher air pressure occurs. In 2.5 mm and 3.0 mm main whole diameters, compressed air occupies a smaller area of the nozzle comparing to the 2.0 mm and the air tends to move near the nozzle walls. Therefore, the exterior air is sucked into the main hole and the negative air pressure originates in larger region at the nozzle inlet. The enlarging of the suction region is agreed with the observations of Patnaik et al.⁵ in larger main hole.

As the injector diameter increases, the suction effect weakens at the nozzle inlet (Figure 15). As it was stated in the literature, the suction effect is getting smaller along the nozzle centre and the air pressure further increases close to the nozzle walls Jeon.²⁶

In the literature, Zeng & Yu^4,25 state that suction is essential to draw the yarn and fibres into the nozzle. However, a longer suction zone results in fibre curving and hinders the fibres wrapping. Therefore, numerical analysis results should be evaluated with the yarn properties to get a decision about the effect of suction on yarn quality.

The airflow character coming from the nozzle injectors

The pressurized air sent from the injectors into the nozzle is divided into two parts and one part goes through the nozzle inlet while another passes towards the nozzle outlet (Figure 16). Both air flows are acting with swirling through the nozzle and creating a kind of helical streamlines inside the nozzle. Helical streamlines of swirling airflow are observed in all nozzle types. Actually, the compressed air coming from the injectors rotates near the nozzle walls. Therefore, the airflow at the walls sucks the air from the outside into the nozzle and causes a suction effect or negative airflow, in particular, at the nozzle inlet. The pressure and intension of this mentioned suction effect changes depending on the nozzle configuration.

(a)                            (b)

(c)

Figure 15 The changes in the air pressure values of the nozzles having 0.5 mm (a), 1.0 mm (b) and 1.5 mm (c) injector diameters.

(a)                            (b)

(c)

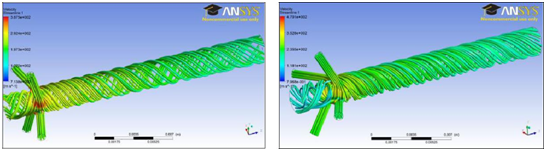
Figure 16 The changes in the air velocity of the nozzles having 15˚ (a), 30˚ (b) and 45˚ (c) injector angles.

Helical streamlines shown in Figure 16 and the animations indicate that the amount of air leaving from the nozzle increases as the injector angle increases. The pressurized air follows a swirling path about the nozzle walls and density of the swirling steps increase at the 15˚. In 45˚, the air moves inside the nozzle and hence follows a shorter way and the air goes through the nozzle outlet. Therefore, the more air leaves from the nozzle in 45˚ injector angle at the same duration. Once the injector angle decreases, the airflow moves with larger steps in the nozzle and the density of the helical streamlines lessens at the downstream of the nozzle.

In the main hole of 2.0 mm, the compressed air fills the all nozzle volume and thus the helical streamlines displays an intensive distribution in the nozzle in comparison to the other main holes.

As the injector diameter increases, the character and density of the streamlines changes along the nozzle length. Mass flow value of the pressurized air increases associated with the injector diameters. In the meantime, the airflow moves with larger steps inside the nozzle and so the density of streamlines decreases.

The airflow character coming from the nozzle inlet or main hole

Regarding to the pressurized air sent from the injectors, there are not considerably significant differences between the nozzles. However, airflow structure and properties, coming from the outside and acting inside the nozzle, sometimes leads to the appreciable differences in the nozzles.

At the nozzle inlet region, some air is sucked from the surrounding medium of the nozzle. Then the air is started to act into the nozzle without any outstanding swirling motion. At the injector region, some part of the air returns and goes towards the nozzle inlet with a swirling motion. It is believed that this case is resulted from the interactions between the airflows sent from the injectors and sucked from the nozzle inlet or main hole (Figure 17).

On the other hand, the airflow sucked from the nozzle inlet is forced to swirl by the pressurized airflow sent from the injectors and thus two types of rotating airflow are created at the injector outlet. One of the airflow is moving towards the nozzle centre and the other is rotating around this airflow. Actually, an airflow structure arises moving in form of the one within the other and having different air velocities. The airflow form of the one within the other leads to the sandwich and bulky, but regular airflow structure having intensive streamlines. The airflow coming from the nozzle inlet moves inside the nozzle associated with the filling to the nozzle interior while the airflow sent from the injectors swirls at the nozzle walls.

Both the airflow leaving from the nozzle inlet and also airflow form of the one within the other are observed at the nozzles having 15˚ injector angle, 2.5 mm and 3.0 mm main whole diameters, injector diameters of 0.5 mm and 0.8 mm. It is expected that these mentioned airflow structures are able to bend the protruding fibres which causes the deteriorating the yarn quality and improve the yarn properties in terms of the binding these fibres to the yarn body.

(a)                            (b)

(c)

Figure 17 The changes in the air velocity of the nozzles having 15˚ (a), 30˚ (b) and 45˚ (c) injector angles.

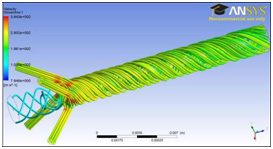
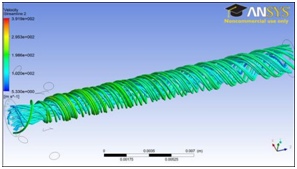
Once the main whole diameter increases, the place is enlarged between the airflows acting on the nozzle wall and around the yarn. And a transition region is occurred. In particular, the airflow coming from the nozzle injectors and acting on the nozzle wall rotates the airflow sucked from the main hole. Therefore, stratified airflow form arises with different flow variables. This mentioned airflow characters cause a bulky structure in 2.5 mm and 3.0 mm main whole diameters while there is more compact fluid flow in 2.0 mm (Figure 18). However, the streamlines of the airflow almost comes a straight line state at the nozzle outlet as the main whole decreases.

(a)                            (b)

(c)

Figure 18 The changes in the air velocity of the nozzles having 2.0 mm (a), 2.5 mm (b) and 3.0 mm (c) main whole diameters.

The airflow character at the nozzle outlet

Airflow velocity decreases towards the nozzle outlet. Sometimes, the airflow leaves from the nozzle slowly and thus it is accumulated and heaped at the nozzle outlet. In some of the nozzles, the airflow returns interior of the nozzle and then moves with swirling motion to the nozzle outlet (Figure 19b). This case is observed in the nozzles with 15˚ and 45˚ injector angles, 2.5 mm and 3.0 mm main whole diameters and 0.5 mm and 0.8 mm injector diameters.

(a)

(b)                            (c)

Figure 19 The airflow at the nozzle outlet for changes 2.0 mm (a) and 2.5 mm (b) main whole diameters.

The air pressure inside the nozzle is lower than the pressure outside the nozzle and the difference in air pressures causes the accumulating or returning of the airflow. These fluid flow motions increase the airflow intensity and therefore projected fibres will get an interaction with more airflow and so yarn quality could be improved.

The airflow character on the yarn

In all analysed nozzles, a boundary layer generates as a thin layer having lower air pressure and velocity values at the nozzle walls and also on to the yarn. The airflow strikes to the nozzle at the boundary layer and its pressure and velocity reduces and the fluid flow is being a laminar flow (Figure 20). Therefore, air velocity on the yarn is considerably lower and it is almost equal to the production speed of the Jetring spinning machine. However, the airflows coming from the nozzle injectors and main hole swirl with higher air velocities.

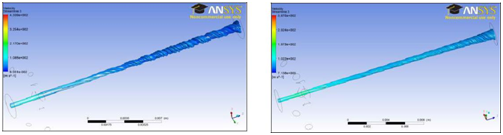
When the airflow on the yarn is analysed, it was found that the air goes forward without swirling from nozzle inlet to the injectors (Figure 21). Suction effect at the nozzle inlet leads to this airflow case. And then the airflow starts to swirl beyond the injectors and moves to the nozzle outlet. Particularly, in 2.0 mm main hole and the nozzles having 1.0 mm and larger injector diameters, the air starts to rotate at the nozzle inlet. On the other hand, as it is seen in Figure 22b, the airflow shows a regular distribution on the yarn and covers the yarn completely. We expected that this airflow character may improve the yarn quality. However, in larger injector diameters and also lower main whole diameters, the airflow rotates a few turns around the yarn and helical streamlines distributes less on the yarn surface (Figure 21d).

Figure 20 Airflow profiles in the nozzle.

(a)                            (b)

(c)                            (d)

(e)

Figure 21 The changes in airflow on the yarn for 0.5 mm (a), 0.8 mm (b), 1.0 mm (c), 1.2 mm (d) and 1.5 mm (e) injector diameters.

The air velocity in the nozzles

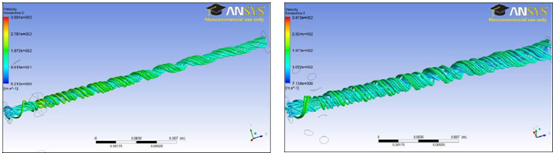
The velocity of the airflow consists of the axial, tangential and radial components. The velocity of the airflows in the nozzle is resultant of these components. In Figure 22, it is given the changes in axial (a), tangential (b) and radial (c) air velocities of the nozzle having 45˚ injector angle. In all the nozzles, it is observed similar changing trend.

As it is seen in Figure 22, radial and tangential air velocities show similar changes along the nozzle length while axial air velocity has a different trend. There is not a significant variation in the radial and tangential velocities at the section between the nozzle inlet and injectors. Following to the injectors, the velocities show a different variation at the nozzle walls. However, similar to the changes in air pressure results, the axial velocity component takes the highest values close to the nozzle walls along the nozzle length. Then the velocity decreases towards the nozzle centre. Axial velocity component has higher values than the other components and hence affects the resultant air velocity more. Resultant air velocity follows similar trend and this result is agreed with the literature Zeng & Yu.²⁵

(a)                            (b)

(c)

Figure 22 The changes in radial (a), tangential (b) and axial (c) air velocities.

On the other hand, the resultant air velocity is not constant along the nozzle length. As we mentioned, it was defined three different airflow characters along the nozzle. Therefore, the airflow velocity is being either higher or lower depending on the nozzle parts. In particular, the air velocity rises at the injector region in terms of the pressurized air coming from the injectors. However, the status of the velocity changes at the nozzle inlet and outlet according to the structural parameters of the nozzle.

The air velocity at the nozzle injectors varies between 177-240 m/s ranges. In comparison to the studied nozzles in the work, the nozzle having 3.0 mm main hole has the highest while the nozzle with 1.5 mm injector diameter gives the lowest velocity value. These mentioned velocity values show similarity with the findings in the literature Zeng & Yu²⁵ Rengasamy et al.⁸ Guo & Yu.¹⁰ The velocity of the airflow coming from the main whole displays in larger ranges and maximum velocity values are 114-332 m/s. 45˚ gives the lowest while the nozzle with 1.5 mm main whole diameter has the highest air velocity values. At the nozzle outlet, air velocity values are between 121-290 m/s and 0.5 mm injector diameter has the lowest and 1.5 mm injector diameter produces the highest air velocity values.

At the nozzle injectors, maximum and minimum velocity values of the airflow are almost the same. However, there are significant differences in the maximum and minimum velocity values of the airflow at the nozzle inlet and outlet. This trend is determined at the nozzles with 2.0 mm main whole diameter or 1.5 mm injector diameter which represents a kind of extreme diameters. Contrary to the other nozzles, these mentioned nozzles have higher air velocity values at the nozzle inlet than that of the nozzle injectors. Therefore, we expected that the air velocity values at the nozzle sections will affect the yarn properties.

The Mach number

The Mach number is an important value in the analysis of fluid flow dynamics problems where the compressibility is a significant factor Cengel & Cimbala.¹ Mach number is a dimensionless value and defined as the ratio of the fluid flow velocity to the speed of sound.

In Figure 23, it is given the changes in Mach number for the nozzles having different injector angles. As it was obtained in air density results, Mach number is not constant along the nozzle length and takes different values depending on the nozzle section. Mach number is very low between the nozzle inlet and injectors. In 30˚ and 45˚ injector angles, Mach number increases by the pressurized air. However, this increase occurs beyond the injectors in 15˚. Following to the injectors, Mach number takes its maximum values at the nozzle walls while it is lower at the nozzle centres.

(a)                            (b)

(c)

Figure 23 The changes in the Mach number of the nozzles having 15˚ (a), 30˚ (b) and 45˚ (c) injector angles.

According to the CFX analysis, Mach number is 0.6-0.64 at the injectors, 0.19-0.55 at the nozzle inlet while 0.18-0.63 at the nozzle outlet. Although Mach number shows a large distribution at the nozzle inlet and outlet, the values concentrate on 0.46 at the nozzle inlet and 0.3 at the outlet. According to the Mach number values, the flow velocity is lower than the speed of sound and the speed can be called as subsonic. Regarding with the numerical analysis of the airflow in the nozzles, it was stated that Mach number is large and changing with the range of 0.6-0.9 for 2.5×105 Pa Guo et al.^9-11

1.5 mm which is the highest injector diameter gives the highest Mach number at the nozzle inlet and outlet and the lowest value at the injectors. On the other hand, 45˚ injector angle and 3.0 mm main whole diameter produces the highest Mach number at the injectors.

Jetring is a spinning system consisting of the three components: nozzle, compressed air and the yarn. Present work aimed to simulate the airflow and determine the flow variables inside the nozzle. In literature, many researchers also worked on the analysis of the airflow character in the nozzle either experimentally or computationally. Our work, based on the numerical analysis of the nozzle, differs from the literature regarding to three contributing causes: type of the solution algorithm, boundary condition-solution validation and modelling of the yarn inside the nozzle. In particular, in order to insure the validation of the numerical analysis, computed and measured mass flow values of the pressurized air were compared. It was found that calculated and measured values are almost compatible. The regression coefficient representing the relation between the computed and measured data is 62.15%. Nevertheless, the values are not completely the same as we desired. There are differences in the values and the differences are reaching up to 2-3 times resulting from nozzle configuration associated with the air density value. During the mass flow measurements, the air density is assumed as constant and equal to 1.18 kg/m³. However, CFD analysis results indicate that air density value changes along the nozzle length and the values are considerably higher than the value taken into consideration in the measurements.

At the end of the study, it was found that the pressurized air swirls with different rotating directions in upstream and downstream of the nozzle. In the nozzle, different types of airflow arise in different parts of the nozzle and flow variables such as velocity and pressure of the airflows are also different. One of them is the airflow sent from the injectors and moving on the nozzle walls. Another one is coming from the nozzle inlet and under the effect of airflow getting from the injectors. The last one is the airflow around the yarn. In particular, the nozzles having different structural parameters differ from each other concerning with the airflow coming from the nozzle inlet and moving on the yarn.

Depending on the structural parameters of the nozzle, airflow sometimes moves near the nozzle walls and this case causes the suction effect on the nozzle inlet. Additionally, the airflow sucked from the nozzle inlet is forced to swirl by the pressurized airflow sent from the injectors and thus two types of rotating airflow are created at the injector outlet. One of the airflow is moving towards the nozzle centre and the other is rotating around this airflow. Contrary to this one within the other airflow form, compact fluid flow structure was observed in some of the nozzles. On the other hand, nozzle configuration sometimes leads to the airflow structure accumulating at the nozzle outlet. In some of the nozzles, the airflow returns interior of the nozzle and then moves with swirling motion to the nozzle outlet. When the airflow on the yarn is analysed, it was observed regular and intensive airflow distribution on the yarn while the airflow rotates a few turns around the yarn in larger injector diameters and also lower main whole diameters. All these airflow characters may affect the yarn properties.

The velocity of the air reaches up to 240 m/s at the injectors of the nozzles. The airflow at the nozzle inlet have the velocity varies between 114-332 m/s, while the air velocity values are between 121-290 m/s at the nozzle outlet. Particularly, it was determined that the differences in the nozzles arise from the airflow at the nozzle inlet and outlet. On the other hand, numerical analysis results show that air density value changes along the nozzle length in all nozzle types and its value is about 1.9-2.14 kg/m³ at the injectors, 1.16-1.3 kg/m³ at the nozzle inlet while 1.09-1.25 kg/m³ at the nozzle outlet. According to the Mach number results which are a significant factor in compressible flows, the flow velocity is lower than the speed of sound and the speed can be called as subsonic. Similar to the air density values, Mach number is also takes different values depending on the nozzle section.

Following to the numerical analysis realized in this study, experimental test results indicate that behavior of the pressurized air in the nozzle affects the yarn properties significantly. In particular, number of the protruding fibres from the yarn body changes.

This work was supported by the grants from Unit of Scientific Research Projects of Isparta in Turkey (Project No: 1795-D-09) and The Scientific and Technological Research Council of Turkey (Project No:109M372). The authors also wish to express their thanks Ekrem Gülsevincler for his collaboration.

There is no conflict of interest.

1. Cengel Y, Cimbala JM. Fluid Mechanics: Fundamentals and Applications. 3rd ed. McGraw Hill Higher Education; 2005. p. 864.
2. Aeschliman DP, Oberkampf WL. Experimental Methodology for Computational Fluid Dynamics Code Validation. AIAA J. 1998;36(5):733.
3. Fokeer S. An Investigation Of Geometrically Induced Swirl Applied To Lean Phase Pneumatic Flows. University of Nottingham, phD Thesis, UK; 2006. p. 347.
4. Zeng YC, Yu CW. Numerical and Experimental Study on Reducing Yarn Hairiness With The Jet Ring and Jet Wind. Textile Research J. 2004;74(3):222‒226.
5. Patnaik A, Rengasamy RS, Kohari VK, et al. Hairiness Reduction of Yarns by Nozzles At Ring Spinning Airflow Simulation Approach. JTATM. 2005;4(4):1‒11.
6. Patnaik A, Rengasamy RS, Kothari VK, et al. Airflow Simulation in Nozzle For Hairiness Reduction of Ring Spun Yarns. Part II: Influence of Nozzle Parameters. J Textile Institute. 2006;97(1):97‒101.
7. Rengasamy RS, Kothari VK, Patnaik A, et al. Airflow Simulation in Nozzle for Hairiness Reduction of Ring Spun Yarns. Part I: Influence of Airflow Direction, Nozzle Distance, and Air Pressure. J Textile Institute. 2006;97(1):89‒96.
8. Rengasamy RS, Patnaik A, Anandjiwala RD. Simulation of Airflow in Nozzle-Ring Spinning Using Computational Fluid Dynamics: Study on Reduction in Yarn Hairiness and the Role of Air Drag Forces and Angle of Impact of Air Current. Textile Research J. 2008;78(5):412‒420.
9. Guo HF, Chen ZY, Yu CW. Numerical Study of an Air-Jet Spinning Nozzle with a Slotting-Tube. J Physics: Conference Series. 2007;96:1‒5.
10. Guo HF, Chen ZY, Yu CW. Simulation of the Effect of Geometric Parameters on Tangentially Injected Swirling Pipe Airflow. Computers & Fluids. 2009;38:1917‒1924.
11. Guo HF, Chen ZY, Yu CW. Numerical Study of the Function of the Slotting-Tube in Air-Jet Spinning. J Textile Institute. 2009;101(3):197‒203.
12. Zou ZY, Cheng LD, Xue WL, et al. A Study of the Twisted Strength of the Whirled Airflow in Murata Vortex Spinning. Textile Research J. 2008;78(8):682‒687.
13. Pei Z, Yu C. Study on the Principle of Yarn Formation of Murata Vortex Spinning Numerical Simulation. Textile Research J. 2009;70(14):1274‒1280.
14. Pei Z, Yu C. Numerical Study on the Effect of Nozzle Pressure and Yarn Delivery Speed on the Fiber Motion in the Nozzle Of Murata Vortex Spinning. J Fluids & Structures. 2011;27(1):121‒133.
15. ANSYS. ANSYS CFX-Solver Theory Guide. ANSYS Inc, USA; 2010. p. 121.
16. Garg VK, Ameri AA. Two-Equation Turbulence Models for Prediction of Heat Transfer on a Transonic Turbine Blade. International J Heat & Mass Transfer. 2001;22:593‒602.
17. Dhinsa K, Bailey C, Pericleous K. Investigation into the Performance of Turbulence Models for Fluid Flow and Heat Transfer Phenomena in Electronic Applications. 20th IEEE SEMI-THERM Symposium. 2004;28(4):686‒699.
18. Haque A, Ahmad F, Yamada S, et al. Assessment of Turbulence Models for Turbulent Flow over Backward Facing Step. Proceedings of the World Congress on Engineering 2007. WCE 2007, London, UK; 2007.
19. Guo HF, An X, Yu CW. Numerical Study on the Principle of Yarn Formation in Murata Air-Jet Spinning. J Textile Engineering. 2007;53(5):173‒178.
20. Wilcox DC. Turbulence Modeling For CFD. 2nd ed.USA: DCW; 1998. p. 1‒477.
21. Bartosiewicz Y, Aidoun Z, Desevaux P, et al.  Numerical And Experimental Investigations On Supersonic Ejectors. International J Heat & Fluid Flow. 2005;36(25):56‒70.
22. Menter FR. Two-Equation Eddy-Viscosiy Turbulence Models For Engineering Applications AIAA J. 1994;32(8):1598‒1605.
23. Cadorin M, Morini M, Pinelli M. Numerical Analyses of High Reynolds Number Flow of High Pressure Fuel Gas Through Rough Pipes. International J of Hydrogen Energy. 2010;35(14):7568‒7579.
24. Oxenham W, Basu A. Effect of Jet Design on the Properties of Air-Jet Spun Yarns. Textile Research J. 1993;63(11):674‒678.
25. Zeng YC, Yu CW. Numerical Simulation of Air Flow in the Nozzle of an Air-Jet Spinning Machine. Textile Research J 2003;73(4):350‒356.
26. Jeon BS. Effect of an Air-Suction Nozzle on Yarn Hairiness and Quality. Textile Research J. 2000;70(11):1019‒1024.