The aim of this study is to reach closer results to the actual measurements by using artificial neural networks in evaluating the properties of single and double layer woven fabrics that affect the end user. The variation of the most important parameters such as breaking strength, weight, thickness, tearing strength properties to meet the end user’s needs depending on the yarn count and the weaving type was investigated. In the fabrics produced in this study, cotton yarn was used as weft yarn in three different numbers and 90 denier polyester yarns were used as warp yarn. Plain, twill, panama, warp rips and satin were used as weaving type. Fabrics were weaved in three different weft frequencies. Evaluations using artificial neural networks were found to give closer results to the actual measurements.

Keywords: cotton, comfort, breaking strength, tear strength, thickness, weight

Comfort properties of the fabrics come out as the first consideration of the user after their color factor with the developing technology and the consciousness of users. Production of the functional products compatible with the movements and daily life of users has become very important. Cotton materials are the best evaluated products in terms of comfort. Parameters that affect the comfort characteristics of fabrics have been studied by many researchers.^1‒9 The clothing comfort depending on these parameters is evaluated within the clothing physiology.^10‒12

The aim of the science of clothing physiology is to create rules for clothing design and production which will not affect the comfort and working efficiency of the person negatively and even contribute to the healing, taking into consideration the fashion and sales parameters.¹⁰ Clothing comfort is defined as the user's feeling of being physically and psychologically comfortable within the current working conditions of user.^10,13‒15

Different techniques such as correlation analysis, regression analysis, factor analysis, artificial neural networks, and fuzzy logic were used to analyze the comfort of clothes.¹⁰ Correlation analysis determines the relationship and direction between variables. In regression analysis, the function of relationship can be determined by considering dependent and independent variables.^10,16 Factor analysis is a technique that allows obtaining a small number of but independent variable sets by combining moderately or highly related variables with each other. It is thus possible to reduce many variables to a few clusters or sizes.¹⁰ The multiple logic system that determines the realization rates of daily living variables is expressed as fuzzy logic. In fuzzy logic, infinite number of propositions can be made. In fuzzy logic, infinite number of gray between black and white is evaluated.^10,17

It is difficult to estimate comfort with these statistical methods, which are used due to nonlinear relations between comfort and fabric parameters. This non-linear relationship is explained by Pontrelli. In his study, Pontrelli has declared that comfortable feeling is due to the invisible parameters such as environmental factors depending on the relationship between environment and fabric characteristics, psychological and physiological factors depending on purpose and appearance of fabrics as well as the user's experience and expectations.¹⁸ In order to overcome this restriction, the relationship between fabric structures and comfort properties is evaluated with artificial neural network. Artificial neural networks are systems that can learn using examples and determine the reaction to environmental effects.

Artificial neural networks are used in learning, associating, classifying, generalizing, characterizing and optimizing operations similar to those that the human brain can do.¹⁰ Detailed information on the basic principles of artificial neural networks and their work has been given in many articles.¹⁹

The human nervous system in the working system of artificial neural networks is taken into consideration and three layers (input, intermediate, and output) are introduced into the network. The measured parameters form the input layer and are used to train the system. The intermediate layer is the part of training itself and is used to obtain output. The output layer expresses the outputs that are reached through the input parameters considered.^10,20
Artificial neural networks have advantages such as short-time application and self-training according to new situations. Artificial neural networks can be classified as forward-feed, back-feed, and forward-feed-back artificial neural networks.^10,21,22 It is preferred to use forward feed-back propagation neural networks, when the comfort characteristics are determined.

Wong et al. reported that artificial neural networks, which can be used in evaluating the comfort of clothes, are fast, flexible and predictive techniques in terms of self-training ability and also estimation of sensory comfort.^10,23

In his study, Tokarska used artificial neural networks to evaluate permeability of fabrics depending on some constructional parameters such as fabric density and twisting parameters of warp and weft yarns. As a result, he stated that the input parameters affected air permeability.²⁴ In a study, thermal conductivity and thermal absorbency parameters were estimated to determine the effect of raw material and knitting construction on comfort properties by using artificial neural networks.²⁵ In another study, weaving construction type, densities and counts of warp and weft yarns, weight and thickness data were used as input material and two artificial neural networks were used in estimating the thermal resistances of the fabric.²² Majumdar used artificial neural network to estimate of thermal conductivity of bamboo and cotton fabrics. Fabric knitting structure, yarn count, ratio of raw material, fabric thickness and weight were used as input parameters in the artificial neural networks.^10,26 Park et al. used seven mechanical parameters measured with KES-F system as input parameters, and artificial neural network was used to estimate tactile sensation of users.^10,27 Yaman et al. used artificial neural network in the hand evaluation of the bulky materials. Friction, compression, thermal properties both wet and dry forms and also wettability properties of disposable diapers were used as input parameters in their study.¹⁹ The effect of the plasma treatment on the comfort characteristics of the fabric has also been examined and it has been shown that the surface properties of the fabric determine the comfort parameters.²⁸

In this study, artificial neural networks were used to estimate the breaking and tearing behaviors of fabrics by using the yarn number, frequency, weight and thickness parameters of single and double layered fabrics with different constructions woven from polyester/cotton yarns by considering the cost factor and the speed required by the age.

Ne 16/1, 20/1 and 30/1 100% cotton yarns were used as weft yarns while 90 denier 100% polyester yarns were used as warp yarns in the fabrics produced in this study. All fabrics were weaved in 160cm reed width and with 160/2 reed number. The fabrics were weaved as single and double layer fabrics by using plain, twill, rips, panama and satin weavings. Fabrics were produced at weft frequencies of 20-60 wire/cm depending on the type of weaving and yarn counts. The fabric widths were measured after 24hours from the end of the weaving process. The technical characteristics of the fabrics produced in this study are given in Tables 1-5.

Physical and comfort tests were conducted at 20±2˚C temperature and 65±5% relative humidity. The frequencies of the fabrics were counted by threading from samples cut to contain at least 100 yarns in the amount of frequency using the Method a specified in TS 250 EN 1049-2. Thickness measurement was performed with a hand type thickness gauge at three different points of the fabric and the average of the obtained values ​​was taken. Thickness measurement was made with 3 repetitions. In the determination of the weights of the fabrics, 15x 15cm² pieces were cut from 3 different parts to represent all samples. The pneumatically operated square meter cutter cuts 100cm² of the sample and weighed it on a digital precision scale. Fabric tensile strength was measured according to TS EN ISO 13934-1, three samples were taken on both sides (in the weft and warp direction) to include different weft and warp threads on the fabric. Samples were taken from the edges of the samples to a thickness of 50mm. After setting the speed of the elongation rate constant (CRE) device to 100mm/min and the distance between jaws to 200mm, the samples were tested with pre-stress of 2-5N. The data was automatically retrieved from the device. Tear strength test was fulfilled according to TS EN ISO 13937-2. Three samples were taken in both directions (in the weft and warp direction) to include different weft and warp threads. The specimens were subjected to a tear test after the elongation rate constant (CRE) was set to 100mm/min at a distance of 100mm from the jaws. The data was automatically retrieved from the device.

The weaving factor values ​​of the fabrics are calculated according to the following formula, which we derived from the weaving factor formula given in the literature.²⁸ The calculated weaving factors were evaluated as input parameters in this study and used in artificial neural networks. Artificial neural networks were performed to estimate breaking and tearing strength of the fabrics by using weft and warp density, weft yarn number, weaving type and weaving factor as input parameters.

The weights and thicknesses of the woven fabrics were measured as indicated in the material section and are shown in Figures 1-3.

Figure 1 Weight values of the single-layered fabrics (g/m²).

Figure 2 Weight values of the double-layered fabrics (g/m²).

Figure 3 Thickness values of the single and double layered fabrics (mm).

It has been observed that the weights of fabrics produced in the work increased with the increase of warp and weft frequency and decreased with the increase of weft yarn number. It has been observed that the number of fabric types and number of fabric layers play a role in the change of fabric thickness. It is seen that the most important parameter in the change of the fabric width is the connection type in the fabric braid. Amount of connection type in fabric constructions are given in Table 6.

It is observed that the most important parameters in changing the fabric width are the weft density, the number of fabric layers, and the type 1 and type 2 connection quantities. Fabric width stretch is larger in the fabrics having more type 5 connection than having more type 1 connection’. For this reason, the fabrics having lowest width are plain fabrics, while the fabrics that have the largest fabric width are rips.

The tensile strengths in the weft and warp direction of the fabrics weaved in the study are shown in Figure 4 & 5, and the tearing strengths are shown in Figure 6 & 7.

Figure 4 Warp and weft direction tensile strength of single-layered fabrics (N).

Figure 5 Warp and weft direction tensile strength of double-layered fabrics (N).

Figure 6 Warp and weft direction tearing strength of single-layered fabrics (N).

Figure 7 Warp and weft direction tearing strength of double-layered fabrics (N).

In the regression analysis, it was seen that the weft tensile strength of both single and double-layered fabrics was affected negatively by the weft yarn numbers while being affected from the weft density in the positive direction. It was determined that the effect of the weaving factor on the fabric tensile strength was negligibly small. The reason why there was no change in the warp tensile strengths was that the same warp set was used in all fabrics.
The change in warp tensile strength values ​​arises only from differences in fabric width due to weaving type. The statistical evaluation showed that the weft tearing strength was influenced by the fabric layer number, weft yarn number, weft connection type, and weft and warp frequency. The higher type 5 and type 1 connection type affects the weft tearing strength positively. In type 5 and type 1 connection, the weft yarn has been held between two warp yarns and they have become closer to each other, which makes tearing more difficult. As the number of fabric layers increases, the tearing of the weft yarns will have become more difficult because of the increase in the bunch formation ratio. Weft yarn number and weft frequency parameters affect the negative direction.

The reason why weft tearing was not occur in double-layered panama fabrics was the overlaying of a large number of weft threads due to the low threading frequency.

• Artificial neural networks application

Artificial neural networks were applied by taking the yarn number, weft frequency, warp frequency and fabric layer number parameters as input parameters and weight, thickness, tensile strength and tearing strength as output parameters. The sigmoid transfer function,$f\left(x\right)=\frac{1}{1+e^{-x}}$ , was used in the study. Separate artificial neural network procedures have been run for weight, thickness, tensile and tearing strength.

• Evaluation of fabrics weight and thicknesses parameters with artificial neural networks:
  While weft yarn number, weft and warp density, number of layer and weaving factor were used as input parameters, thickness and weight values measured were used as output parameters to evaluate fabric weight and thickness with artificial neural networks.

The sigmoid algorithm was used in the hidden layer for artificial neural networks in this study. The structure of the applied artificial neural networks is shown in Figure 8. Relationship between measured and calculated with artificial neural networks is shown in Figures 9 & 10 for fabric weight and thickness, respectively.

Figure 8 Artificial neural networks model for fabric weight and thickness (MLP 5:5-9-1:1).

Figure 9 Relationship weight values between measured and calculated with artificial neural networks.

Figure 10 Relationship thickness values between measured and calculated with artificial neural networks.

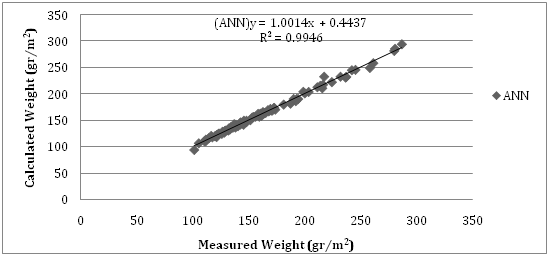
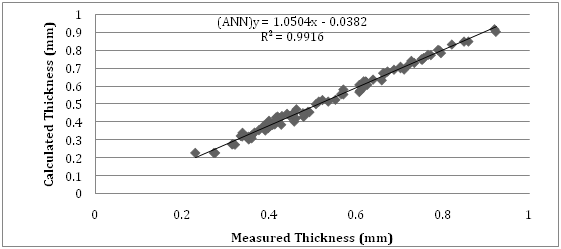
The square root of the error squares (RMSE) values, calculated as formula $RMSE=\sqrt{\raisebox{1ex}{${\displaystyle {\sum }_{i=1}^n\left(x_H-x_{Ö}\right)}$}\!\left/ \!\raisebox{-1ex}{$N$}\right.}$ , and are given in Table 7. As you seen in Table 7, the fabric weight and thickness values ​​calculated using artificial neural networks were close to real/measured values ​​at R²=0.9946 and R²=0.9916, respectively.

Because the calculated RMSE values ​​are very low, it can be said that the weight and thickness parameters calculated with artificial neural networks reflect the actual measurement results.

Evaluation of tensile strength parameter with artificial neural networks: While weft yarn number, weft and warp density, weaving factor, thickness and weight were used as input parameters, tensile strength both warp and weft direction measured were used as output parameters to evaluate fabric tensile strength properties with artificial neural networks.

The sigmoid algorithm was used in the hidden layer for artificial neural networks in this study. The structure of the applied artificial neural networks is shown in Figure 11. Relationship between measured and calculated with artificial neural networks is shown in Figure 12.

Figure 11 Artificial neural networks model for warp and weft tensile strength (MLP 6:6-11-1:1).

Figure 12 Warp and weft tensile strength values calculated with artificial neural networks (N).

The RMSE values for both warp and weft tensile strength are given in Table 8. As you seen in Table 8, the fabric tensile strength values calculated both weft and warp directions by using artificial neural networks were close to real/measured values ​​at R²=0.9988 and R²=0.9969, respectively.

Because the calculated RMSE values ​​are very low, it can be said that tensile strength parameters calculated with artificial neural networks reflect the actual measurement results.

Evaluation of tearing strength parameter with artificial neural networks: While weft yarn number, weft and warp density, weaving factor, thickness and number of layer were used as input parameters, tearing strength both warp and weft direction measured were used as output parameters to evaluate fabric tearing strength properties with artificial neural networks.

The sigmoid algorithm was used in the hidden layer for artificial neural networks in this study. The structure of the applied artificial neural networks is shown in Figure 13. Relationship between measured and calculated with artificial neural networks is shown in Figure 14.

Figure 13 Artificial neural networks model for warp and weft tensile strength (MLP 6:6-9-1:1).

Figure 14 Warp and weft tearing strength values calculated with artificial neural networks (N).

The RMSE values for both warp and weft tearing strength are given in Table 9. As you seen in Table 9, the fabric tearing strength values calculated both weft and warp directions by using artificial neural networks were close to real/measured values ​​at R²=0.9964 and R²=0.9944, respectively.

Because the calculated RMSE values ​​are very low, it can be said that tensile strength parameters calculated with artificial neural networks reflect the actual measurement results.

1. It is seen that the fabric density values ​​affect the fabric weight in the positive direction while the yarn counts affect the negative direction.
2. It is seen that the most important parameter in the change of the fabric width is the connection type in the fabric braid.
3. The most important parameter for fabric width is the count of type 5 connection.
4. The most important parameters for tensile strength is weft density. On the other hand, weaving factor can be neglect for this parameter because of very small effect.
5. It is seen that the counts of type 5, type 1 connection and layers of the fabrics affect tearing strength of the all fabrics positively.
6. The fabric weight, fabric width, tensile and tearing strength values ​​calculated with artificial neural networks were found to be closer to real values.

This study was supported by UBAP06 2015/TP004 Project, Usak University. Some tests were made in the UBATAM in Usak University.

Author declares there is no conflict of interest in publishing the article.

1. Demiryürek O, Uysaltürk D. Investigation of explosive strength and pilling properties of Viloft/Polyester blended fabrics. Textile and Engineer. 2016;23(102):105‒111.
2. http://www.kelheim-fibres.com/produkte/vi_te_uk.php
3. Demiryurek, O, Uysalturk D. Thermal comfort properties of viloft/cotton and viloft/polyester blended knitted fabrics. Textile Research J. 2013;83(16):1740‒1753.
4. Demiryurek O, Uysalturk D. Statistical analyses and properties of viloft/polyester and viloft/cotton blended ring-spun yarns. Fibres & Textiles in Eastern Europe. 2014;22(1):22‒27.
5. Can Y, Kırtay E. Yarn properties affecting the tear strength of cotton woolen fabrics. Afyon Kocatepe University. Journal of Science. 2009;7(2):65‒78.
6. Şekerden F, Çelik, N. Weft elastane weaving and fabric characteristics. Ege University Textile & Apparel J. 2010;20(2):120‒129.
7. Raj S, Sreenivasan S. Total wear comfort index as an objective parameter for characterization of overall wearability of cotton fabrics. J Engineered Fibers & Fabrics. 2009;4(4):29‒41.
8. Haiging M, Xiang Z. Influence of weave on fabric wrinkle recovery property before and after resin treatment. J Donghua University. 2001;(4):18‒20.
9. Kaplan S, Göktepe Ö. Yarn structure and the effects of the fabric construction on the strength properties of the woven fabric. Textile Marathon. 2002;11(6):37‒47.
10. Utkun E. A Review of Literature About the Use of Artificial Neural Networks Systems on Prediction of Clothing Comfort. Pamukkale University J Engineering Sciences. 2014;20(7):272‒280.
11. Kaplan S, Okur A. The meaning and importance of clothing comfort: a case study for Turkey. J Sensory Studies. 2008;23(5):688‒706.
12. Utkun E. Development of clothing for the comfort of babies from 0-1 years of age (infant). PhD Thesis, Ege University, Izmir, Turkey; 2013.
13. Sweeney MM, Branson DH. Sensorial comfort, Part I: A psychophysical method for assessing moisture sensation in clothing. Textile Research J. 1990;60(7):371‒377.
14. Li Y. The Science of Clothing Comfort. Textile Institute Publications, Textile Progress. 2001;31(1‒2):1‒135.
15. Liao X, Hu J, Li Y, et al. A review on fabric smoothness-roughness sensation studies. J Fiber Bioengineering & Informatics. 2011;4(2):105‒114.
16. Tekin VN. Introduction to Statistics. Istanbul, Turkey: Distinguished Publishing; 2008.
17. Ünal C. Evaluation of work and personnel in confection with fuzzy logic application. Izmir, Turkey: PhD Thesis; 2009.
18. Pontrelli GJ. Comfort by design. Textile Asia. 1990;21(1):52‒61.
19. Yaman N, Şenol MF, Gürkan P. Applying Artificial Neural Networks to Total Hand Evaluation of Disposable Diapers. J Engineered Fibers & Fabrics. 2011;6(1):38‒43.
20. Öztemel E. Artificial neural networks. Istanbul, Turkey: Chamomile Education Publishing; 2006.
21. Özdemir H. Artificial Neural Networks and Its Use in Weaving Technology. Electronic J Textile Technologies. 2013;7(1):51‒68.
22. Bhattacharjee D, Kothari VK. A neural network system for prediction of thermal resistance of textile fabrics. Textile Research J. 2007;77(1):4‒12.
23. Wong ASW, Li Y, Yeung PKW, et al. Neural network predictions of human psychological perceptions of clothing sensory comfort. Textile Research J. 2003;73(1):31‒37.
24. Tokarska M. Neural model of the permeability features of woven fabrics. Textile Research J. 2004;74(12):1045‒1048.
25. Güneşoğlu S. Investigating the comfort features of sportswear. PhD Thesis, Uludag University, Bursa, Turkey; 2005.
26. Majumdar A. Modelling of thermal conductivity of knitted fabrics made of cotton-bamboo yarns using artificial neural network. J Textile Institute. 2011;102(9):752‒762.
27. Park SW, Hwang YG, Kang BC, et al. Applying fuzzy logic and neural networks to total hand evaluation of knitted fabrics. Textile Research J. 2000;70(8):675‒681.
28. Yaman N, Özdoğan E, Seventekin N. Improving Physical Properties of Polyamide Fibers by Using Atmospheric Plasma Treatments. Textile & Apparel. 2012;2:102‒105.