The quality of the denim fabric is a phenomenon that requires successfully meeting several properties at the same time; among these properties are air permeability and water resistance. Very little study has been carried out on multiple properties and parameters at the same time. In this study, we used Response Surface Methodology to optimize levels of thickness and optimum and levels of fabric mass per unit area which simultaneously maximize water resistance and minimize air permeability of denim cotton fabric.

A response surface methodology was employed for data analysis experimental results of denim cotton fabric. A set of expressions expressed by contours plot was obtained for predicting the water resistance and air permeability performances of denim fabric quality as a function of fabric thickness and fabric mass per unit area. Those fabric’ figures were optimized by first graphical approach based on overlaid contour plot and second by the desirability function approach to achieve maximum water resistance and minimum air permeability simultaneously.

The usage of denim fabric has been increasing all over the world because it is simple and quick to manufacture and has low production costs. In addition, it is more comfortable, the fabric structure is resistant, and its fashion versatility and the variety of products that can be produced with it are superior. Optimization techniques referred to as the optimum solution ensure the production of the best solution. End use and the fulfilment of customer expectations are important concerns in the textile industry. This evolution of the production of the denim fabric has led to a survey of this material being undertaken to improve its quality. Several studies using neural networks and statistical package programs as an alternate approach to predicting problems in denim fabrics are available in the literature.^1–3

Among the various mechanical and physical properties of fabrics, water resistance and air permeability performances are very important. In the relevant literature, many factors affecting the water resistance and air permeability of fabric were investigated. Most of them focused on yarn and fabric properties.^4–6

On the other hand, Principal Component Analysis method,⁷ factorial experimental design⁸ artificial neural network.⁹ Artificial neural networks deal with the estimation of a fitted response to a process.

Apart from these studies, Msahli and al.,¹⁰ optimized the effects of yarn type of fabric by Taguchi design technique.

Response surface (RS) is a method used for modeling the relationship between process inputs and output factors to predict responses and to optimize the process input factors.¹¹

Water resistance and air permeability are two major quality characteristics of fabrics comfort affected by fabric thickness and fabric mass per unit area, were examined in terms of fitted response surfaces.

The RSM is important in designing, formulating, developing, and analyzing new scientific studying and products.¹² It is also efficient in the improvement of existing studies and products.

In the current study the effect of fabric thickness and fabric mass per unit area on the water resistance and air permeability for a denim cotton fabric was examined by RS optimization procedure, and the desirability function technique employed to determine the optimum levels of fabric thickness and mass per unit area maximizing the water resistance and minimizing air permeability. To the best of our knowledge this is the first study that maximizes water resistance and minimizing air permeability by the using multi response optimization method.

Materials

Ten different denim cotton fabrics samples were studied in total and they were laid on a flat surface in atmospheric condition for relaxation.

All experiments were carried out in a standard atmosphere of 65% RH and 20±2˚C temperature for testing according to Standard ISO139. The characteristics of the yarns were determined: weft and warp yarn counts, weft and warp yarn twist factor. The following characteristics of fabrics were determined: weft and warp yarn density, Thickness and mass per unit area. The mean mass per unit area was determined in accordance with Standard EN 12127. Similarly the thickness was determined in accordance with Standard EN ISO 5084.

Those main characteristics are given in Table 1.

The air permeability measurement

The air permeability was determined by an Air Permeability Tester. Tester following EN ISO 9237 test standards with a 100kPa pressure difference. Five samples from each fabric type were tested. The air permeability of a fabric is defined as the amount of air passed over a surface under a certain pressure difference in a unit time. This value has significance with respect to the usage area.

This test method covers the measurement of the air permeability the rate of air flow passing perpendicularly through a known area under a prescribed air pressure differential between the two surfaces of a material of textile fabrics and is applicable to most fabrics. It is generally expressed in ml/cm²/sec.

The water resistance measurement

Circular specimen of area 100cm² were prepared and measured according to ISO 811. The water penetration resistance was determined by Hydrostatic pressure test. It is a hydrostatic pressure method for determining the resistance of fabrics to penetration by water.

A specimen is subjected to a steadily increasing pressure of water on one face, under standard conditions, until penetration occurs in three places. The hydrostatic head supported by a fabric is a measure of the resistance to the passage of water through the fabric.

All denim fabrics were investigated after 24h relaxation in a free state in standard atmospheric conditions. The levels of variables like fabric thickness, and fabric mass per unit area are chosen based on the common denim application. 

Methods

In the current study, the Response surface methodology is used, it is an experimental modelling technique dedicated to the evaluation of the connection of a set of controlled experimental factors and observed results. Prior knowledge of the process is required in order to achieve a satisfactory statistical model. A detailed account of this technique has been outlined.^13–18 The first goal for Response Surface Method is to find the optimum response. When there is more than one response then it is important to find the compromise optimum that does not optimize only one response. When there are constraints on the design data, then the experimental design has to meet requirements of the constraints. The second goal is to understand how the response changes in a given direction by adjusting the design variables. In general, the response surface can be visualized graphically. The graph is helpful to see the shape of a response surface; hills, valleys, and ridge lines.

In the current study, the significant variables of fabric thickness and fabric mass per unit area were chosen as the critical variables and designated as X1 and X2 respectively to reach the desired level of water resistance and air permeability by two techniques, graphical approach and desirability functions.

Graphical approach

In the first optimization, the overlaid contour plots are used. This Graphical superimposition method is not only easy to understand and use, but also straightforward. First of all, for each response, a response contour is obtained by fitting, in general, the second-order response model. Then by superimposition of response contours, we arrive at optimal conditions. Even though this procedure is practically very useful, it is difficult to apply when the number of input variables exceeds three, and to identify one set of conditions or one point in the experimental region as being optimal.

Desirability function

In the second stage, we performed the optimization by using the desirability function dependent on two factors. The objective given to each property of the denim fabrics so as to maximize, minimize, or reach a target value, the acceptance interval defining the lower and upper limits for each property in which the requirement level set by the consumer is met and the consumer is satisfied.

Derringer and Suich,¹⁹ described a multi response optimization technique employing some composite functions which are called desirability functions. If a particular fitted response is to be maximized, minimized, or assigned a target value then the functions in Figures 1–3 are employed respectively in the Table 2.

Figure 1 Desirability function to maximize.

Figure 2 Desirability function to minimize.

Figure 3 Function of desirability to reach a target value.

This concept is widely used in solutions where it is necessary to combine various characteristics (properties) that have different units and different scales. The Harrington function allows converting physical parameters to the psychological scale of desirability. Desirability is defined in the range (0, 1).

In this study, to combine the different individual desirability function for each criterion in only one value, the function of global desirability of Derringen & Suich²⁰ is used and definite in formula (4) that takes into account the importance of each criterion in the global satisfaction degree.

$d_G=\sqrt[\text{w}]{{\text{d}}_{\text{1}}{}^{\text{w1}}{\text{x d}}_{\text{2}}{}^{\text{w2}}\text{x}\dots {\text{x d}}_{\text{m}}{}^{\text{wm}}}$     (4)

With:

d_i: the function of individual desirability of the criterion y_i

w_i: the weight of the criteria y_i in the global desirability function d_G.

$w={\displaystyle \sum _1^m{w}_i}$     (5)

The compromise between the different criteria is better when "d_G" increases, it becomes "perfect" when "d_G" is equal to 1. When the satisfaction degree "d_i" of the criteria Y_i is equal to 0, so "d_G" is equal to 0 and so the compromise is rejected.

In the current studies, the determination of the optimum levels of fabric thickness and optimum levels of fabric mass per unit area which simultaneously maximize water resistance and minimize air permeability of denim cotton fabric is an important problem. The Minitab Response Optimizer Software was employed for solutions of this problem the results of the different measured properties are represented in Table 3 for the studied fabrics.

The experimental results have been statistically evaluated using Analysis of Variance (ANOVA) with F values at a significance level of α=0.005 with the intention of exploring whether or not there was any statistically significant difference within the variation obtained.

The analysis of variance (ANOVA) technique was used to check the effects of fabric thickness, and fabric mass per unit area on water resistance and on air permeability. And F-ratios were calculated at the 95% level of confidence by using MS Excel software 2007. Details are given in Table 4 and Table 5.

We evaluated the results based on the F ratio and the probability thereof (prob>F).

The lower the probability of the F-ratio, the stronger the contribution of the variation and the more significant the variable. The fabric mass per unit area has the big contribution on water resistance and air permeability compared to the fabric thickness. 

Individual responses optimization

The studied quality characteristics (water resistance and air permeability) affected by fabric thickness and fabric mass per unit area, were examined in terms of fitted response surfaces in Figures 4,5. By examining these figures, the optimum values of fabric thickness and fabric mass per unit that maximize water resistance and minimize air permeability simultaneously can be estimated to some degree.

In Figure 4, the effect of fabric thickness and fabric mass per unit area on water resistance of denim cotton fabric is illustrated as a graph.

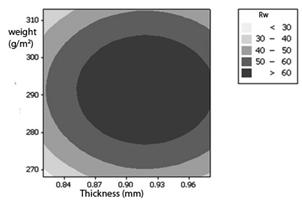
Figure 4 Response surface plot showing the effect of fabric’s thickness and fabric’s mass per unit area on water resistance of denim cotton fabrics.

Response surface plot (Figure 5), shows that minimum air permeability is occurred for studied fabric, for lowest fabric thickness value and fabric mass per unit area around 300g/m².

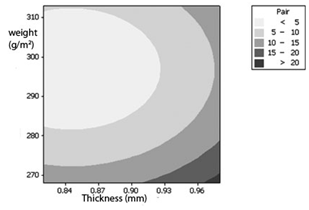
Figure 5 Response surface plot showing the effect of fabric’s thickness and fabric’s mass per unit area on air permeability of denim cotton fabrics.

In Figure 5, the effect of fabric thickness and fabric mass per unit area on air permeability of denim cotton fabric is illustrated as a graph.

In general, the individual optimum responses are contradictory and a compromise must sought. It enables zones simultaneously satisfying all of the selected properties.

Multiresponses optimization

The object of the multiresponse optimization is to determine conditions on the input variables that lead to optimal or nearly optimal values of the response variables.

Simultaneous optimization techniques are used when there is more than one response variable and it is necessary to find the ‘optimum points’ of the factors that fulfil all requirements for all response variables at the same time. The results of the multiresponse optimisation of the studied properties are given by graphical superimposed method and by desirability functions method.

The target value and limits of the selected properties are represented in Table 6. The desirable level fabric performance of water resistance and air permeability is defined in terms of the intended end use and, ultimately, by the user.

Table 6 denotes the interval bounds for water permeability and air permeability.

After finding the contour plot of each response, we superimposed these diagrams to get the overlaid contour plot of different studied fabric properties. This overlaid contour plot permits to find a compromise zones and the best factor values (thickness and fabric mass per unit area) that optimise simultaneously the selected properties. So, we tried to find graphically the domains, which the fabric properties affecting denim fabric quality will be in the tolerance intervals. In this diagram the white zone represents the compromise zone, where all properties are in the objective that means the compromise of all properties is satisfied.²¹

The result of the overlaid contour plot is represented in the Figure 6 for the water resistance and the air permeability. For the studied fabrics and for the objectives as represented in Table 6, Figure 6 presents the white zone for satisfying studied properties (compromise zone). According to this figure, the optimum parameters of thickness and weight, need to be respectively belonging [0.94;0.98] and [298;305].

Figure 6 Overlaid plot for water resistance and air permeability of denim fabric.

With the help of Minitab 15 software response optimization values were determined. Based on this study, to achieve the maximum water resistance, the global solution would be a fabric thickness of 0.9 mm and fabric mass per unit area of 290g/m². To achieve the minimum air permeability, the global solution would be a fabric thickness of 0.8 mm and fabric mass per unit area of 310g/m².

But in Figures 4&5, the response surfaces have saddle (minimax) system, thus the determinations of the optimum level of the fabric thickness and mass per unit have some difficulties. These optimization problems can be solved by employing the desirability function technique as describe before.

Most researchers use a graphical approach of superimposing the different response surfaces and finding the experimental region that gives the desired values for all response variables simultaneously. This methodology, although visually attractive, is inefficient and cannot be automated for this reason; optimization of the selected properties by the desirability function will be done.

Desirability function optimization

Another important procedure discussed here, also implemented in Minitab, is the desirability function approach. In this approach the value of each response for a given combination of controllable factors is first translated to a number between zero and one known as individual desirability. Individual desirability functions are different for different objective types which might be Maximization, Minimization or Target.

Simultaneous optimization using the desirability function technique is recommended tool.^22,23 It is based on the idea that the ‘quality’ of a product or process has multiple quality characteristics.²⁴ The desirability approach, proposed initially by Derringer & Suich,²⁰ seems very promising for optimizing simultaneous response variables, besides being easily performed 24. The general approach consists in first converting each response variable into a desirability function di, that varies from 0 to 1.²⁵ The factor levels that take to a maximum or a minimum of the response variable are called ‘optimum points’.

In the current study, after calculating individual desirability (di) for water resistance and air permeability, as described in the formula (1) and (2) we have combined them to provide a measure of the composite, or overall, desirability, that desirability are given in the Figure 7. This measure of composite desirability (the combined desirability) is the weighted geometric mean of the individual desirability for the studied properties.

Figure 7 Individual and combined desirability functions.

Consequently, for the studied fabrics, we can estimate the compromise, according to the consumer requirements and the importance degree assigned to every selected fabric property. The desirability values depend on the objective of every property, on the acceptance intervals and on the requirement of the consumer. This desirability value can be used as consumer’s index for the studied properties of denim fabric.

This method can be also used for other kind of fabrics to foresee the consumer’s satisfaction according to the end user needs.

The optimal solution for a better compromise for the studied properties for a specified application can then be determined by maximizing the composite desirability.

The optimum levels of fabric thickness and fabric mass per unit area for maximum water permeability and minimum air permeability of denim fabrics are given Figure 8.

Figure 8 Optimum points of fabric thickness and fabric mass per unit area.

The optimal combination of factors was found to be fabric thickness 0.98 mm and fabric mass per unit area 305g/m².

3D plot of the overall desirability function

We propose a 3D plot of the overall desirability function d(x) for the (x1, x2) plane as presented in the Figure 9. The function d(x) is quite "flat" in the vicinity of the optimal solution, indicating that small variations around the optimum solutions are predicted to not change the overall desirability drastically. However, the importance of performing confirmatory runs at the estimated optimal operating conditions should be emphasized.

Figure 9 Overall Desirability Function.

The best solution [Fabric thickness, Fabric mass per unit area] is [0.98mm, 300g/m²] and the overall desirability for this solution is 0.596. All responses are predicted to be within the desired limits.

In this study we tried to optimize in the same time two main properties of denim fabric which are the water resistance and the air permeability. This approach takes into account the fabric end uses by defining the targets and limits of each property.

In this study, optimum fabric thickness and mass per unit area values that make water resistance maximum and air permeability performance minimum at the same time are estimated by Response Surface Method, a kind of multi response optimization method using two approaches.

This optimization permits. The first method is the graphical approach by the overlaid contour plot by finding compromise zones. Effects of input variables affecting water permeability and air permeability were assessed by response surface plots and overlaid contour plot to obtain a compromise zone satisfying the targeted values of the selected properties. For the studied denim cotton fabric, the best compromise is obtained at the thickness and fabric weight belonging to the intervals [0.94; 0.98] and [298;305], respectively. The second method is by using the desirability function to obtain the optimum level of fabric thickness and fabric mass per unit area [0.98mm and 305g/m²] to maximize water resistance and to minimize the air permeability simultaneously.

Those approaches will provide tools using graphical method and numerical method to assess contribution of different properties in the same time. Thus, the producer will have a mean that allows him, according to the targeted consumer, to adjust his product in order to reach the wished property.

None.

1. Halleb N, Sahnoun M, Cheikhrouhou M. The effect of washing treatments on the sensory properties of denim fabric. Textile Research Journal. 2015;85(2);150–159.
2. Gazzah M, Jaouachi B, Sakli F. Study of the friction effects on residual bagged denim fabric behavior. The journal of textile institute. 2014:95–96.
3. Cheriaa R, Baffoun A. Effects of cross linkers combination, for three dimensional effects, on denim garment properties. Fibers and polymers. 2015;16(5):1150–1155.
4. Jaouachi B. Study of spliced elastic denim yarn performances, 6/13. Journal of natural fibers. 2013;10(3):233–243.
5. Kheder F, Dhouib S, Sakli F. The effect of seaming on cloth shrinkage during finishing treatment of denim garments. Research journal of textile and apparel. 2013;17(4):90–102.
6. Gazzah M, Jaouachi B, Sakli F. Effect of frictional parameters on the residual bagging behavior of denim fabrics. International Journal of Applied Research on Textile. 2015;3(1):32–43.
7. Gazzah M, Jaouachi B, Schacher L, et al. Study of the influential inputs on the bagged denim fabric behaviors using the principal component analysis method. International journal of clothing science and technology. 2015;27(6):922–939.
8. Moussa A, Ben Marzoug I, Bouchareb H, et al. Development and optimization of waterproof breathable double-sided knitting using a factorial experimental design. Journal of Industrial textiles. 2015;45(3):437–466.
9. Souid H, Babay A, Sahnoun M. Fabric quality optimization by using desirability function and neural networks. International journal of Computer technology and applications. 2012;3(1):356–364.
10. Msahli S, Hadj Taieb A, Sakli F. A new approach for predicting the knit global quality by using the desirability function and neural networks. Journal of the Textile Institute. 2006;97(1):17–23.
11. Zaouali R, Msahli S., and Sakli, F. A nonlinear viscoelastic model for describing fabric wrinkle recovery behavior. International Journal of Applied Research on Textile. 2014;2(2):22–32.
12. Halleb N, Sahnoun M, Cheikhrouhou M. Validation of tactile sensory panel. International Journal of Applied Research on Textile. 2014;2(1):30–42.
13. Annadurai G, Sheeja RY. Use of Box- Behnken design of experiments for the adsorption of verofix red using biopolymer. Bioprocess Engineering. 1998;18(6):463–466.
14. Box GEP, Behnken DW. Some new three level design for the study of quantitative variables. Technometrics. 1960;2(4):4-55-475.
15. Box GEP. Multifactor designs of first order. Biometrika. 1952;39(1–2):49–57.
16. Box GEP, Draper NR. A basis for the selection of a response surf­ace design. J Amer Stat Assoc. 1959;54(28):622–654.
17. Box GEP, Wilson KB. On the experimental attainment of optimum conditions. J Roy Statist Soc. 1957;13(1):1–45.
18. Box GEP, Hunter JS. Multifactor experimental design for exploring response surfaces. Ann Math Statistics. 1957;28(1):195–241.
19. Derringer G, Suich R. Simultaneous optimization of several response variables. Journal of Quality Technology. 1980;12(4):214–219.
20. Phan-Than-Luu R. Methodology of the experimental research. Spain: Euskatel Estatistika; 1993:127–134.
21. Yang K, Yang K, Tao XM, et al. The optimization of working parameters of Nu-Torque TM singles ring knitting yarn using response surface methodology. Roubaix: World Textile conference 4th AUTEX conference; 2004.
22. Calado V, Montgomery DC. Planejamento de Experimentos usando o Statistica. 1st ed. E-papers ServiSc os Editoriais Ltda; 20030 260 p. ISBN 978-85-8792-283-0.
23. Cruz AG, Faria JAF, Walter EHM. Processing optimization of probiotic yogurt supplemented with glucose oxidase using response surface methodology. Journal of Dairy Science. 2010;93(11):5059–5068.
24. Reis FR, Masson ML, Waszczynskyj N. Influence of a blanching pretreatment on color, oil uptake and water activity of potato sticks, and its optimization. Journal of Food Process Engineering. 2008;31(6):833–852.
25. Granato D, Castro IA, Ellendersen LSN, et al. Physical stability assessment and sensory optimization of a dairy-free emulsion using response surface methodology. Journal of Food Science. 2010;73(3):149–155.