Brain tumors are the second leading cause of cancer-related deaths in children and young adults. About 37% of the brain tumors are malignant, causing brain cancers. Current standard of cure includes surgery, radiotherapy and chemotherapy. Brain surgery is too complex and involves more risks in treatment. In external beam radiation therapy, multiple treatments of standard-dose fractions of radiation are applied to the brain. This process is repeated for a total of 10 to 30 treatments, depending on the type of tumor. Chemotherapy may improve overall survival in patients with the most malignant primary brain tumors. However, it does so in only about 20% of the patients. Chemotherapy is often used in young children instead of radiation, as radiation may have negative effects on the developing brain. Thus, there is a critical need for alternate/new therapies, and Electrochemotheraphy is an attractive alternative. By applying electric field at critical strength across cell membrane, it is shown to make it permeable to anti-cancer drugs. In this study, the electric field distribution of human brain is investigated using commercial, state-of-the-art, COMSOL software that utilizes finite element method, with variable parameters like tissue conductivity and permeability. The electric field distribution on tumor regions at various depths (slices) were examined for two types of electrode geometries, viz., needle and microelectrode configurations. The needle electrodes showed the max intensity of 1600V/cm at the 0 cm slice, while the microelectrodes showed reduced values. These results could be used for clinical applications.

Our body is electric and it is possible to elicit both therapeutic and diagnostic phenomena using electrical pulses of appropriate magnitude and frequency (duration). The use of electrical fields to treat brain cancer is gaining momentum.^1,2 Electrical fields were also used in Israel to treat brain tumors successfully, with twice the median time to recur of the cancer and the overall survival period.¹ At Yale University, alternating electric fields were used to arrest cell proliferation in human brain tumors.² This is possible because living cells consist of ions, polar or charged molecules, membranes, and organelles, and they are responsive to electric fields of appropriate magnitudes and frequencies therapeutically.^1‒3 The electric activity of cells plays a key role in many essential biological processes, which could be utilized to treat cancer also, using application of electrical pulses. This kind of alternate, novel, and physical therapies are critical to treat brain tumors as 20-40% of all other cancers later develop brain metastasis⁴ in addition, for children and young adults at ages 20-29, brain cancer is the 2nd leading cause of death.^5,6 There are millions of people worldwide suffering from the brain tumor morbidities and mortalities and it necessitates the application of electrical-pulse-mediated therapy known as electrochemotherapy.^7‒9 This involves application of high intensity, short duration pulses after injection of a low dose chemo drug to render the plasma membranes permeable to otherwise impermeable drugs. Up to 1000 fold enhancement in drug uptake is observed: hence, electrical-pulse-mediated chemotherapy has a lot of promise as a tool to treat brain tumors effectively and economically. Towards this, we study the electric field distribution in brain tumors under various conditions. It is important to study the electric field distribution, as, if the field intensity is low, the drug could not get into the cells; if the field intensity is high, the cells will be killed, hence for effective drug delivery, the optimum field conditions is necessary and the distribution of this electric field intensity depends on type of electrodes. We studied the electric field distribution of brain tumor using needle and microneedle electrodes, at various depths of the tumor.¹⁰

3D Model

A three-dimentional (3D) model consisting of the human brain, tumor tissue and electrodes was developed to study electric field distribution. Figure 1a shows a brain tumor configuration.¹¹ This is modeled as shown in Figure 1b. Here, the upper electrode (positive) and the lower electrode (ground) are used to apply voltages. The electric field distribution using two needle electrode and microneedle electrode array was studied. The dimensions of model components along with the voltages applied in each case (to obtain a nominal value of 1200V/cm⁷) are listed in Table 1 and the electrical parameters in Table 2.¹²

Figure 1 Brain Tumor (a) [11] and the 3D Brain Model (b) created for simulation.

Software

In order to determine the electric field distribution inside the tumor and other layers of brain, a three-dimensional finite element model (Figure 2) was implemented in the COMSOL software package (COMSOL Multiphysics, V.4.3b; Stockholm, Sweden). COMSOL solves a series of equations for solving the given problem. The governing equations that COMSOL uses to compute electric field (E) are given as follows:

$\nabla D=\rho V$ (1)

$D={\epsilon }_0{\epsilon }_{r}E$ (2)

$E=-\nabla V$ (3)

Figure 2 Slices of brain consisting tumor across thickness (Z-Axis).

where, D is electric displacement, r is the electrical charge density, eo is the permittivity of free space, and er is the relative permittivity of the medium. Electrostatics (es) module of AC/DC physics in COMSOL is used to compute electric field while varying geometry, voltage and some other parameters. The electrical boundary conditions along the tissue in contact with the energized electrode were ϕ=V0 (electrode voltage) and ϕ= 0 at the ground electrode. The boundaries where the analyzed domain was not in contact with an electrode were treated as electrically isolative.

Figure 3 shows a typical distribution of the electric field along the depth using microneedle array electrode. The electric field intensity varies from a lower value at the bottom to a higher value at the top. It is the highest at the tip of the needles. The variation of the electric field distributions for the two electrode configurations, namely, the two needle, and microneedle array electrodes, are shown in Figures 4a-4c, at the 0.25cm, 0cm, and -0.25cm slices respectively (the slices were cut at 0, 0.25, 0.5, 0.75, -0.25, -0.5, and -0.75cm). The electric field intensity is the highest at 121.6V/cm for the two needle electrodes and 7.79V/cm for the microneedle array electrodes, at +0.25 cm slice. At 0cm, the maximum electric field intensities for these electrode configurations are, 1603.1 and 434.49V/cm, respectively. The electric field intensity is highest at the needle configuration due to the sharp edge of the needle. The electric fields at -0.25 cm slice are, 604.86, and 487.64V/cm respectively for the two electrode types. This indicates the variation of the electric field intensity along the tumor thickness, maximum being at the surface where the electrodes are placed (in the center of the tumor, at 0cm) and they vary in magnitudes above and below 0 cm, as shown for 0.25cm and -0.25cm. Figure 5 shows a comparison of average electric field for the two needle electrode at +0.25, 0, and -0.25cm layers along the depth. The variation is highly non-linear from -0.25 to 0 to +0.25 cm depths. It is only 7.6% at +0.25cm, compared to the magnitude at 0 cm, while it is 37.7% at -0.25cm, compared to that at 0 cm. Similar variation is also observed for the microneedle electrode array (Figure 6). In this case it varies to a low 1.8% at the +0.25cm level compared to 0 cm level. However, at -0.2cm level, it is more than at 0 cm level, it is of 112.22% of that of at 0cm level. These variations could be due to the difference in the electrode geometry and their penetration into the tumor thickness at various slice levels. The applied voltage can be varied to obtain desired field intensities.

Figure 3 Electric field distribution along the axes of the brain tumor model.

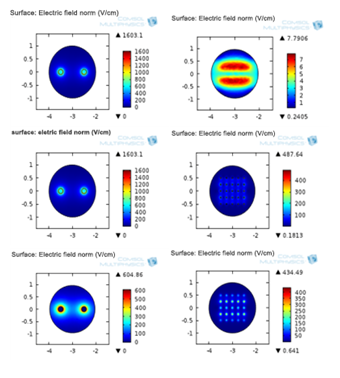
Figure 4 Electric field distribution at +0.25 (a), 0 (b) and -0.25 cm (c) slices for the two needle and microneedle array electrodes.

Figure 5 Comparison of Maximum Electric Field Magnitudes at various depths inside the tumor (1-at +0.25 cm, 2-at 0 cm, 3-at -0.25 cm levels) for the two needle electrode array.

Figure 6 Comparison of Maximum Electric Field Magnitudes at various depths inside the tumor (1-at +0.25 cm, 2-at 0 cm, 3-at -0.25 cm levels) for microneedle electrode array.

Electric field intensities vary at various depths of the tumors. It also varies based on the electrode geometries, viz. two needle and microneedle array electrode configurations. Maximum field intensity of 1603V/cm is obtained for the two needle electrode at slice at 0 cm. The variation is highly non-uniform, from 0 cm to +0.25 cm and -0.25cm levels. For the given configuration, if higher intensities are needed, two needle electrodes are suitable. However, if lower electric field strengths are needed, the microarray needles are preferred. However, by varying the applied voltage, it is possible to obtain desired electric field intensity at a given depth for a given electrode configuration. This study is useful to select the appropriate intensity at the clinic to do electrochemotherapy for brain tumors.

None.

Authors declare there are no conflicts of interest.

1. Brinn D. Israeli therapy kills brain cancer cells with electrical field; 2007.
2. Kirson ED, Dbalý V, Tovarys F, et al. Alternating electric fields arrest cell proliferation in animal tumor models and human brain tumors. Proc Natl Acad Sci U S A. 2007;104(24):10152‒10157.
3. Steve Haltiwanger. Electrical properties of cancer cells; 2010,
4. http://braintumor.org/brain-tumor-information/?gclid=CJeUw6-qxL8CFRARjg
5. Brain Tumor Statistic. American Brain Tumor Association; 2014.
6. Ostrom QT, Gittleman H, Farah P, et al. CBTRUS Statistical Report: Primary Brain and Central Nervous System Tumors Diagnosed in the United States 2006-2010. Neuro-Oncol. 2013;15(sup 2):ii1‒ii56.
7. Larkin JO, Collins CG, Aarons S, et al. Electrochemotherapy: Aspects of Preclinical Development and Early Clinical Experience. Ann Surg. 2007;245(3):469‒479.
8.  Campana LG1, Mocellin S, Basso M, et al. “Bleomycin-Based Electrochemotherapy: Clinical Outcome from a Single Institution’s Experience with 52 Patients. Ann Surg Oncol. 2009;16(1):191‒199.
9. Sundararajan R, Xiao F, Lenarduzzi N, et al. Efficient and Economical Electro-Drug Delivery. IEEE Toronto International Conference-Science and Technology for Humanity:Toronto, USA; 2009. 843-848 p.
10. Wikipedia.org; 2014.
11. http://wisciblog.com/2012/04/10/frequent-dental-x-rays-linked-to-most-common-brain-tumor
12. Agoramurthy P, Sundararajan R. Electric field distribution for human breast tissue, IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP); 2010.