The energy delivered by a swift proton beam in materials of interest to hadron therapy (liquid water, polymethylmethacrylate PMMA, DNA, Adenine and Guanine) is investigated. An explicit condensed-state description of the target excitation spectrum based on the dielectric formalism is used to calculate the energy-loss rate of the beam in the irradiated materials. The model used to the electronic excitation spectrum through its energy loss function (ELF), namely the extended-Drude ELF. The singly differential cross section and the total cross section for ionization, as well as the average energy of the generated secondary electrons, show sizeable differences at T (0.5, 1.0, 2.5, 4.5, 10.0 MeV) when evaluated with these ELF models. In order to know the radial distribution around the proton track of the energy depositedby the cascade of secondary electrons, a simulation has been performed that follows the motion of the electrons through the target taking into account both the inelastic interactions (via electronic ionizations and excitations as well as electron-phonon and electron trapping by polaron creation) and the elastic interactions.

Keywords: hadron therapy, organic compounds, electronic excitation, DNA, proton beams, energy loss function

Projectiles incident on the target do not always induce reaction. Even if reaction occurs, not a specific reaction but many different reactions occur. A specific reaction occurs with a certain probability. This probability is called the cross section.¹ Ion beam cancer therapy (IBCT, or hadron therapy) represents an effective method for providing high-dose delivery into tumours, thereby maximizing the probability of killing the cancer cells whilst simultaneously minimizing the radiation damage to surrounding healthy tissue.² Despite its high cost, proton-beam therapy is widely spread around the world with over 60 operational centres.³ The electronic interactions lead to the ejection of a vast quantity of secondary species, including secondary electrons and free radicals.⁴ To understand the mechanism of radiation induced DNA damage, Monte Carlo track structure simulations are a useful tool to determine spatial and temporal distributions of new chemical species and specific energy deposition densities. These simulations require a completeset of differential cross sections for the respective primary and secondary particles and target materials.⁵

There is currently a great interest in the study of the interaction of energetic particles with subcellular components at micrometric scales,⁶ since there are experimental evidences suggesting that the damage of the cell is not only due to lesions in nuclear DNA, but other cell components are also sensitive to radiation-induced damage. As usually cells are immersed in a nutrient medium, it is very difficult to obtain experimental information on the energy delivered to their different compartments due to the interaction of charged particles.⁷ Not always happen induce reaction when Projectiles incident on the target. Even if reaction occurs, not a specific reaction but many different reactions occur.

This paper is organized as follows. First, in Section 1, we describe a semiempirical model to calculate the energy distribution of the ejected secondary electrons due to the impact of energetic protons in PMMA and four compounds. The present work⁴ is based on the dielectric formalism and assumes that the weak bound electrons of the target can be characterized by a mean binding energy, which allows the calculation of the initial energy distribution of the ejected secondary electrons by the proton impact.⁸ Apart from electronic interactions, ion propagation is influenced by nuclear fragmentation reactions, which convert the initial projectiles in a new whole family of propagating secondary particles. The electronic interactions lead to the ejection of a vast quantity of secondary species, including secondary electrons and free radicals.⁹

A precise knowledge of the angular and energy distribution of secondary electrons ejected from biological materials after swift ion impact is a matter of paramount importance in the development of current radiobiological models aimed at understanding the mechanisms underlying ion beam cancer therapy in secondary electron¹⁰ the following points must be taken in the considerations.

Energy loss functions for organic compound and water

The key quantity for studying the energy deposited in targets of biological interest by swift projectiles, such as photons, electrons, protons, or heavy ions is energy loss function (ELF).¹¹ By using optical data as experimentally can be determined the ELF for all the electronic excitations and ionizations of a target when (zero momentum transfer, k=0) or X-ray and electron energy loss experiments (k≠0).

Tan et al.,¹² perceived that the optical-ELF of four bioorganic condensed compounds and liquid water at low energies (corresponding to the excitation of the outer shell electrons) are rather similar, with an intense peak around 20-25 eV, and sometimes with other small peaks at lower energies. This fact led them to the idea that the experimental optical ELF of the outermost electrons of organic compounds can be parametrized with a single-Drude function.¹³

$\mathrm{Im}\left[\frac{-1}{\in \left(k=0,E\right)}\right]=\frac{a(Z_2)E}{{\left[E^2-E_p^2\left(\overline{Z}\right)\right]}^2+{\gamma }^2\left(\overline{Z}\right)E^2}$ (1)

Where a $(Z_2)$ (in eV³), $E_p(Z_2)$ (in eV) and $\gamma (Z_2)$ in illustrate the intensity, position and width of the single-Drude ELF. Using the experimental optical ELF of the 5 bioorganic compounds, $E_p(\overline{Z})$ and $\gamma (\overline{Z})$ was parametrized as a function of the mean atomic number of the target, $\overline{Z}$ is number of electrons per formula divided by the number of atoms).

$\begin{array}{c}{E}_p=19.927+0.9807\overline{Z},\\ \gamma =13.741+0.3215\overline{Z}\end{array}\}$ (2)

where Z₂ is the mean sum of the atomic number of these organic compounds and liquid water. The $\overline{Z}$ of each compound is calculated and also presented in Table 1.¹³

The remaining parameter, a(Z₂), can be simply obtained by imposing the accomplishment of the f-sum rule, linked to the number of electrons in the target.  Where experimental data for the ELF at the optical limit (i.e., at k=0) are used, while its extrapolation to finite momentum transfers (k≠0) is provided by suitable extension algorithms.

Macroscopic single differential cross section (SDCS) for proton in compound

Let us consider an energetic ion of mass M₁, atomic number Z₁ and charge q, moving with kinetic energy T in a medium it induces electronic excitations and ionizations in the material, losing energy in the process. It is characterised by its dielectric function ε (k, ω). Assuming that the outer shell electrons of the target can be characterised by a mean binding energy B, then a secondary electron will be ejected with a kinetic energy $W=\hslash \omega -B_i$ .¹⁴ Then, the dielectric framework gives the following expression for the ionization single differential cross section (Table 2) (ionization SDCS) $d{\Lambda }_{ionis}/dW$ , or inverse mean free path, for the ejection of an electron with kinetic energy W from the electronic i-shell of the target, by a projectile of kinetic energy T is:⁸

$\frac{d\Lambda \left(T,W\right)}{dW}=\frac{e^2}{\pi {\hslash }^2}\frac{M_1{Z}_1^2}{T}{\displaystyle \underset{k}{\overset{k_{+}}{\int }}\frac{dk}{k}}\mathrm{Im}\left[\frac{-1}{\in \left(k,B_i+W\right)}\right]$ (3)

where e is the elementary charge and we have employed E = Bi + W, with Bi and W being, respectively, the binding energy of the i shell and the kinetic energy of the ejected electron.

$\mathrm{Im}\left[\frac{-1}{\in \left(k,B_i+W\right)}\right]$ is the contribution to the ELF from the i-shell ionization and $\in \left(k,B_i+W\right)$ is the complex dielectric function of the target. The sub-index i in eq (1) refer to the contribution of the electronic shell to the ELF. The integration limits, imposed by conservation laws, are $k_{\mp }=\sqrt{2M_1}\left(\sqrt{T}\mp \sqrt{T-E}\right)$

The macroscopic cross section is related to the microscopic one, σ, thought Ʌ=Nσ where N is the molecular density of the target.⁹ Where

$\frac{d\Lambda }{dw}=N\frac{d\sigma }{dw}$ (4)

These ejected electrons can make further initiating an avalanche effect, ionizations, leading to the energy transfer to sensitive biomolecular targets.¹⁵

Total ionization energy

The total ionization cross section (TICS) is obtained by integrating the single differential cross section between the energy zero and the large energy that can be transferred to the medium in one single interaction noted follows the expression:¹⁶

$\Lambda (T)={\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{d\Lambda \left(T,W\right)}{dW}dw}$ (5)

Average energy

Although the major contribution to the ionization cross section comes from the outer shells, the inner shells can also have noticeable effects in the calculation of some quantities, such as the average energy of ejected electrons,¹⁷

$W_{av}(T)=\frac{1}{\Lambda (T)}{\displaystyle \underset{0}{\overset{\infty }{\int }}W\frac{d\Lambda \left(W\right)}{dW}dW}$ (6)

where $\frac{d\Lambda \left(W\right)}{dW}$ is given in Eq. (3) and from the integration of Eq. (3) over W.

Figure 1 shows the ELF for liquid water, PMMA, DNA, Adenine and Guanine with energy transfer E=ħw in eV at wave number k=0. It is determined optical ELF of five condensed organic compounds with the results obtained through Eq. (2). Good agreement is achieved with previous experimental data for Adenine as shown in Figure 1, the agreement is quite good for all the organic targets, but with larger discrepancies in the case of water. The dominate peak located at proton energy of ~20 ev and weaker one appears at ~(5-10) eV. In figure 2 we show the convoluted differential (in energy) ionization cross section SDCS, for proton beam incident on several representative biological targets: liquid water, DNA, PMMA, Adenine and Guanine by using single Drude model ELF The compositions, densities and mean binding energies of the targets are summarized in Table 1 with an initial energy from Figure 2, comparison of the results using the experimental for Adenine¹³ at 0.5 Mev. It is agree with results of the dielectric formalism ELF.

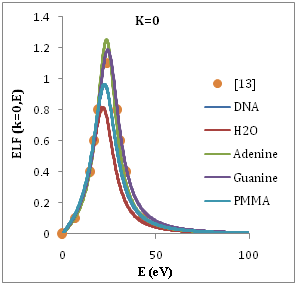
Figure 1 Energy loss function (ELF) of H2O, DNA, Guanine Adenine and PMMA as a function of the transferred energy ħw, for several values of the momentum transfer ħk at k=0.

We present in Figure 2 the calculated SDCS generated in organic compound due to the impact of protons, equation (3), at several energies T of the incident proton beam. The range of proton energies is chosen from (0.5, 1, 2.5, 4.5, 10)Mev we chose these representative energies because they match with those of protons around the Bragg peak when the initial beam energies correspond to those employed in hadron therapy. Without entering into Drude ELF model, first, we can observe that most of the secondary electrons generated are in the low-energy range. Second, the number of generated electrons increases when the proton energy decreases, meaning that at the Bragg peak there is a strong increment in the ionization of the target, being larger than in the plateau of the Bragg curve, where the proton energy is larger. Third, the influence of the target ELF modeling in the ionization-SDCS is larger for lower proton energies.

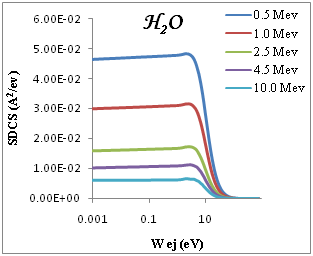
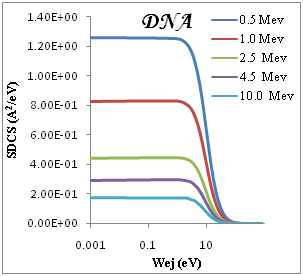
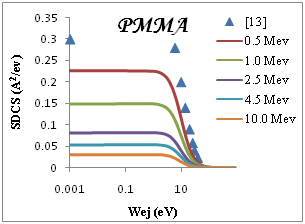
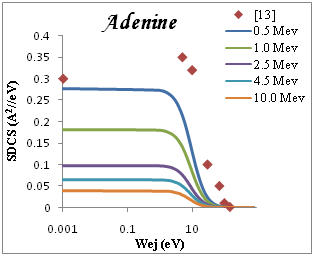
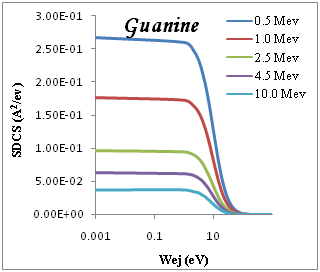
Figure 2 SDCS for liquid water, DNA, PMMA, Adenine and Guanine in different energy as a function of the kinetic energy of the emitted electron.

The ionization SDCS increases when the proton energy decreases, obtaining that the maximum value of SDCS for protons at 0.5Mev is 4.5 times larger that SDCS for protons at 10Mev is 4.5 times larger for 0.5Mev for proton than for 10Mev protons. It is interesting to compare the number of electrons generated by the protons at different energies which is proportional to the total ionization cross section.

If one looks at the existing parameterization’s performed for liquid water,^13,4 it can be seen that the excitations are practically confined at low transferred energies, while at high energies only ionizations remain. Therefore, we can estimate a mean binding energy, B, from the ionization thresholds of all the outer electronic shells, and assume that ionizations will only occur at energies above this threshold (the electron being ejected with an energy (W = E−B), and excitations only below it. This mean binding energy is 18.13 eV for liquid water;¹³ in fact, a few electronvolts above these energy excitations practically vanish, while only ionizations remain.

The SDCS given by eq. (3) is not only valid for the ionization of the i-shell, but it can also account for excitations. It can describe the ionization of an electronic shell i provided that we know the contribution of the ionization of this shell to the total ELF. Since the ELF was obtained in the previous section from an empirical parametrization to experimental ELFs, which include all the possible excitations and ionizations of the target, we need some criterion to distinguish the ionizations from the excitations and evaluate the electron production cross sections.

 We show in Figure 3a-3e the total ionization cross section TICS (i.e., inverse mean free path) calculated for proton impact in five representative biological materials relevant for cancer therapy: liquid water, dry DNA (C₂₀H₂₇N₇O₁₃P₂), PMMA, Adenine and Guanine. The total ionization is calculated using Drude model described (the dielectric formalism ELF) and parameterzation in Table 1. The information depicted in Figure 3a-3e is quite interesting, since it shows the different sensitivities of each target to ion impact ionization. Among the macroscopic targets shown in Figure 3, it seems that Devare et al.,¹³ which nicely agree with our calculations above 100keV. For proton energy T_p=0.1Mev, (T)=0.2, 0.18, 0.16 for DNA, H₂O, PMMA respectively and 0.15 for Adenine and Guanine. We note DNA has the largest TICS,. Nonetheless, DNA show TICS larger than liquid water and another compounds, a fact that could indicate a larger ionization probability of these targets. It is remarkable the possible effect of the larger density of the DNA, but here are considered to have densities similar to that of liquid water. Perhaps, in this case, the dominant factor is the number of electrons per molecule.

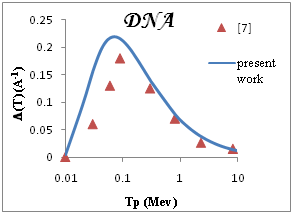
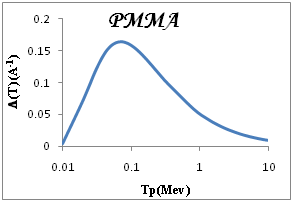
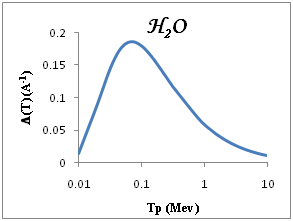
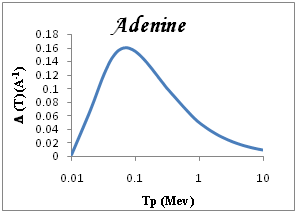
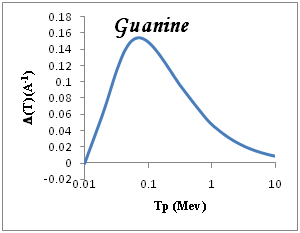
Figure 3 Macroscopic TICS (inverse mean free path), in four biological materials and liquid water in the condensed phase.

We find that the average electron energy increases with the proton energy.¹⁸ According to eq. (6), the high energy transfers will be more relevant in these calculations, so ionization of the inner shells will play a noticeable role.

Figure 4 shows results for five representative biological targets. At T_p(Mev)≥0.1 up to 10Mev $W_{av}(ev)\approx 50$ the near constant for compounds PMMA, H₂O, Adenine and Guanine except $DNA\approx 60ev$ also when $Tp(Mev)\approx 0.01$ W_av (eV) between (5-10 eV) except Guanine W_av< (0.01-0.0).

Figure 4 Average energy of the secondary electrons ejected from different biological materials by proton impact for liquid water and four organic compounds.

In present work we review, explain in more detail and expand our semiempirical method proposed to evaluate the ion impact ionization cross sections for condensed complex biological targets based on the dielectric formalism and a semiempirical parametrization of the experimental optical ELF of organic compounds. Calculations are extended to a broad selection of representative biological targets (liquid water, DNA, adenine, guanine, including the contribution from the inner shells to properly perform the calculation of the average energy of secondary electrons, besides the single differential and total cross sections. Our calculations show good agreement with previous data in the gas phase for water, adenine and they also agree with other semiempirical, theoretical and ab initio calculations at high ejection energies. At low energies, work seems to agree better than the others with the experimental data. We evaluate ionization cross sections and average energies of secondary electrons for all the cited targets, showing some differences between their ionization efficiency, and a quite similar behaviour of the average energy of secondary electrons. This method will be extended in future works to account for heavier ions in different charge states, and also for electron impact.^19-21

I would like to express my thanks to the department of physics in Mustansiriyah University for all the help me.

None.

1. Shuzo Uehara, Hooshang Nikjoo, Dimitris Emfietzoglou. Interaction of radiation of mater. CPR press: USA; 2012. 364 p.
2. M Behar, RC Fadanelli, I Abril, et al. Energy loss of proton, α particle, and electron beams in hafnium dioxide films. Phys Rev A. 2009;80:062901.
3. Eugene Surdutovich, Gustavo Garcia, Nigel Mason, et al. Nano-scale processes behind ion-beam cancer therapy. Eur Phys J. 2016;70(4):86.
4. Nanoscale Insights into Ion-Beam Cancer Therapy. A Solov’yov (Ed.), Springer International; 2017.
5. Bernhardt Ph, Paretzke HG. Calculation of electron impact ionization cross sections of DNA using the Deutsch–Märk and Binary–Encounter–Bethe formalisms. Int J Mass Spectrom. 2003;223-224:599‒611.
6. RM Thomson, A Carlsson Tedgren, JF Williamson. On the biological basis for competing macroscopic dose descriptors for kilovoltage dosimetry: cellular dosimetry for brachytherapy and diagnostic radiology. Phys Med Biol. 2013;58(4):1123.
7. P de Vera, E Surdutovich, I Abril, et al. Analytical model of ionization and energy deposition by proton beams in subcellular compartments. Eur Phys J. 2017;68:96.
8. De VerP, Garcia-Molina R, Abril I. Nanoscale Insights into Ion-Beam Cancer Therapy. Springer International; 2017. 61‒98 p.
9. Emfietzoglou D. Inelastic scattering of charged particles in condensed media: a dielectric theory perspective, Section III in Interaction of Radiation with Matter. H Nikjoo et al. (Ed.), Boca Raton: CRC Press, USA; 2012.
10. P de Vera, E Surdutovich, R Garcia-Molina, et al.Analytical model of ionization and energy deposition by proton beams in subcellular compartments. Eur Phys J. 2014;68:96.
11. R Garcia-Molina, I Abril, I Kyriakou, et al. Inelastic scattering and energy loss of swift electron beams in biologically relevant materials. Surf Interface Anal; 2016.
12. Tan Z, Xia Y, Zhao M, et al. Proton stopping power in a group of bioorganic compounds over the energy range of 0.05–10 MeV. Nucl Instr Meth B. 2006;248(1):1‒6.
13. De Vera, P Abril, I Garcia-MolinaR, et al. Ionization of biomolecular targets by ion impact: input data for radiobiological applications. Journal of Physics: Conference Series. 2013;438:012015.
14. Dapor M, Abril I, De Vera P, et al. Simulation of the secondary electrons energy deposition produced by proton beams in PMMA: influence of the target electronic excitation description. Eur Phys. 2015;69:165.
15. P de Vera, R Garcia-Molina, I Abril, et al. Semiempirical Model for the Ion Impact Ionization of Complex Biological Media. Physical review letters. 2013;110:148104.
16. De Vera, P Abril, I Garcia-MolinaR, et al. Ionization of biomolecular targets by ion impact: input data for radiobiological applications. Journal of Physics: Conference Series. 2013;438:012015.
17. Dapor M, Abril I, De Ver P, et al. International Scholarly and Scientific Research & Innovation. 2016;10:1033‒1037.
18. Maurizio Dapor, Isabel Abril, Pablo de Vera, et al. International Journal of Chemical, Molecular, Nuclear, Materials and Metallurgical Engineering. 2016;10:8.
19. Tan Z, Xia Y, Zhao M, et al. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. Instr Meth in Phys Res B. 2004;222(1‒2):27‒43.
20. De Vera P, Abril I, Garcia-Molina R. J Appl Phys. 2011;109:094901.
21. Pimblott SM, LaVerne JA. Production of low-energy electrons by ionizing radiation. Radiat Phys Chem. 2007;76(8‒9):1244‒1247.