Electroporation is the application of electrical pulses for enhanced drug delivery. When used for delivering chemo drugs, it is called electrochemotherapy (ECT). For inoperable and chemo- and radio-resistant tumors, we need an alternative technique and ECT is a viable option as evidenced by the treatment of thousands of patients, effectively. The efficiency of the ECT depends on the voltage (electric field) magnitude, pulse duration, number of pulses, the drug molecule to be delivered and the electrode geometry and size. It is of practical interest to study the effect of electrode material on the efficacy of the therapy. Towards this, in this research, we investigated the influence of electric field distribution due to different electrode materials. For this purpose, both platinum and surgical steel needle array electrodes were used. Surgical steel is the most commonly used material for electro chemotherapy applications. These needle electrodes are of both hexagonal and pentagonal configurations with a central electrode in each. ANSYS, the industry standard software that uses finite element method is used to study the electric field distribution, of both healthy tissue and tumor tissue using these two electrode configurations and the two different materials. Both unipolar and bipolar voltages were studied. The results indicate that the electric field distribution, both in magnitude and pattern is similar for both electrodes, for both configurations and materials, which is desired from the clinical aspect. The electric field intensities for the hexagonal and pentagonal needle electrodes were 1280V/cm and 1180V/cm respectively in the case of tumor tissue (correlating well with the desired level of 1200V/cm). They were 835V/cm and 843V/cm for these electrodes in the case of healthy tissues. The values were same in the case of bipotential voltages too.

Electrochemotherapy (ECT) is an evolving technique to treat various types of skin, chest wall breast cancer and basal cell carcinoma with minimal side effects.¹ Electrochemotherapy was the only available alternative treatment for patients suffering from lung cancer who are unfit to undergo surgery.² This procedure utilizes hydrophilic chemo drugs such as bleomycin and cisplatin which are aided by electroporation to create apoptosis. ECT has an overall response of 80-90% for un-resectable recurrent disease.^3,4 Typically eight 1200V/cm, 100µs pulses are applied in the clinics. The various parameters which influence the process of electroporation are electric potential (field intensity), pulse width, number of pulses, types of chemo drug, and size and geometry of the tumor.^5–7 In addition, the efficiency of electroporation also depends on the type, size and shape of electrodes. In practice, based on the method of contact, electrodes are classified as surface electrode, needle electrode and flexible laparoscopic electrode.⁸ Based on the geometry, the electrodes are classified as linear array and concentric electrodes. The electrodes play a vital role of connecting the tissue to the electrical pulses. Needle electrodes have better efficiency over surface electrodes for treating deep-seated tumors.⁷ But the surface electrodes provide uniform distribution over needle electrodes, since the point of contact for surface electrode is wider than needle electrode. Within needle electrodes, concentric type of electrodes provides better uniform distribution of electric field over linear array electrodes.⁹ For effective electroporation and to maximize its outcome in the tumor, design and positioning of the electrodes with respect to the tumor becomes a critical factor. Hence, the design of electrodes varies for each case. Electrode design using numerical methods enables the optimized design of electrodes for effective electroporation. Numerical modeling determines optimal parameters even for inhomogeneous tissues which could not be achieved through analytical calculation.⁹ The focus of this work is to determine the effect of material used as electrode apart from its configuration in electroporation. For this purpose, needle electrodes of both surgical steel and platinum were studied for both hexagonal and pentagonal configurations. Surgical steel is the material commonly used in the manufacturing of electrodes. Due to its distinct electrochemical properties, nobility and metallic characteristics; it is used in various medical applications from cranial joints to syringes.^10–12 On the other hand, platinum can also be used as electrode material for its electro-chemical attributes, noble metal (inert) properties and physical properties. However, platinum usage results in the deposition of salts, viz., platinum (IV) chloride, hexachloroplatinate (IV) ammonium, hexahydroxyplatinate (IV) potassium, diaminedinitroplatinum (II), etc.^13,14 These salts are reported to cause various side effects. Platinum salts can also induce bronchoconstriction, anaphylactic shock, elevated plasma histamine levels etc. even without any prior exposure.¹⁵ In addition, platinum is costly. It is of practical interest to study using simulation, the electric field distribution of these two materials.

In this study, two configurations of concentric type needle electrodes are analyzed. Honey comb structured hexagonal array concentric type needle electrode and pentagonal type needle electrode with central anode are analyzed due to the uniform distribution of electric field by these configurations.^9,16,17 The above configurations have also been built and simulated for their electric field distribution. Figure 1 shows the two electrode geometries with central electrode, designed and built. Figure 1A shows the hexagonal electrode array and Figure 1B shows the pentagonal electrode array. These electrodes are modeled and simulated using industry standard software, ANSYS APDL version13.0, 2010, which uses finite element method to do the electric field computation. The electrode configuration with tumor, surrounded by healthy tissue and without tumor are modeled in ANSYS such that the distance between each electrode (d) is very much greater than the diameter (a) of the electrode (d>>a). In ANSYS, the various available types of simulation techniques available are electric, thermo-electric, fluid dynamics, structural, and so on. Electric was used in this research. Then the element property to be applied for the model has to be selected. In this study, 2D quad structure is selected. ANSYS needs the electrical properties, resistivity and relative permittivity of the various materials in the study, including the healthy tissue, the tumor tissue, and the electrode materials. The resistivity of the tumor is considered as 2.5Ω-m and permittivity as 52F/m. For healthy tissue, the resistivity is considered as 5 Ω-m and permittivity as 52F/m.^17,18 The electrical properties of electrodes (both platinum and surgical steel) are provided in the Table 1.^5,17

Figure 1 Electrode geometries of Hexagonal (A) and Pentagonal electrodes, both with central positive electrode.

In addition, the geometry and dimensions of all these materials is also needed. The radius of each electrode was chosen as 0.5mm. The tumor size is 2.5mm. Table 2 gives the various geometry details. For study purpose, the distance between adjacent electrode of same potential (d) and the distance between electrodes of opposing potential (l) are considered to be equal (0.4cm). The electric field applied in the study is a single pulse of 1200V/cm with a pulse width of 100µs. Contour plot is preferred over other output methods since it can provide the uniformity of electric field distribution as well as region of effective electroporation graphically. Both unipolar and bipolar potentials were studied. In the case of unipolar, the central electrode was set at positive voltage (of V=+480V, to get a electric field of, E=V/d = 480/0.4=1200V/cm, for an electrode gap of 0.4cm). The outer electrodes were set to ground voltage (0V). For bipotential, the central electrode was set at +240V and the outer electrodes at -240V, so the total voltage is 480V (240-(-240) =480V). Figure 2 shows the models used for electric field simulation study. Figure 2A shows the central anode configuration of concentric type hexagonal array electrode, and Figure 2B shows the central anode configuration of concentric type pentagonal array electrode.

Figure 2 2D model of hexagonal and pentagonal configurations with tumor.

The 2D contour plots of electric field distribution of platinum electrodes without tumor is shown below in Figure 3 and that of with tumor (surrounded by the healthy tissue) is shown in Figure 4. Figure 3A shows the electric field distribution in the healthy tissue without tumor, when a hexagonal concentric array with central positive electrode is used to apply pulses in the healthy tissue, and Figure 3B, with a pentagonal electrode. It is seen that the electric field did not spread beyond the ground potential electrodes surrounding the anode, in both cases. Thus these configurations provide good coverage and precision in locally targeting the required area. Figures 4A & 4B show the electric field distribution with the tumor. The tumor is considered as a homogeneous structure of circle for easy representation. In practice, the shape of the tumor will be inhomogeneous structure. Here, the maximum electric field is around the positive electrode, which in turn is placed exactly on the tumor. Thus the maximum electric field is rather on the tumor than on the healthy tissue. The electric field distribution of surgical steel electrodes with tumor for these configurations is shown in Figure 5. This matches exactly with the electric field distribution shown in Figure 4, for platinum electrodes. Tables 3 & 4 show a comparison of the max and average electric field intensities for the two electrode configurations and the two materials. There is close correlation between the values at both the healthy tissue and tumor area, indicating that the material does not affect the electric field value, which is good for treating the tumor with various electrode materials. Of course, it is possible that the reaction of the tissue and the drug molecules could be different in the clinical practice. However, as for as the electrochemotherapy is concerned, only the configuration of the electrode geometry matters, not the material.

Figure 3 Contour plot of electric field analysis for platinum electrode over the healthy tissue.

Figure 4 Contour plot of electric field analysis for platinum electrode over the tumor.

Figure 5 Contour plot of electric field analysis for surgical steel electrode over the tumor.

A comparison of our results with the published results in the literature⁹ indicates close correlation in the pattern and magnitude of the electric field. Figure 6 shows results obtained by Corovic et al.⁹ for hexagonal electrode. There is very good similarity in the electric field distribution. There is good correlation of the magnitudes also at various distances (905.4, 928.7, 925.4, 876.9, 875.9V/cm, and so on). The magnitudes vary from 4% to 10% between our and these published values, indicating good correlation between our findings. One-on-one correlation is not possible as the data points are not furnished. Figure 7 & Figure 8 illustrate the comparisons of electric field intensities at various points/distances for hexagonal and pentagonal electrode configurations, respectively, for both platinum and surgical steel electrodes, with and without tumor. They compare the max value of the electric field from center of the tumor to the cathode. Table 5 shows the variation of the max electric field, assuming the value at 0 to be 100%. It reduces at locations 1, 2, and 3 and then increases. The variation is similar for both healthy and tumor tissues and also for both materials for the two electrode geometries. The variation is maximum at the interface of the electrode to tissue due to the noticeable difference in the resistivity and relative permittivity of the two materials. It tapers down in between and then again increases due to the significant difference between the material properties between the tissues and the electrode.

Figure 6 Electric field distribution of hexagonal electrode.⁹

Figure 7 Distance vs electric field of platinum and surgical steel electrode for hexagonal concentric type needle electrode with and without tumor.

Figure 8 Distance vs electric field of platinum and surgical steel electrode for pentagonal concentric type needle electrode with and without tumor.

In addition to unipolar potential, the electric field distribution using bipolar potential was also studied. For this purpose, the central electrode was kept at +240V and the outer electrodes at -240V, compared to +480V and 0V respectively, in the unipolar case. Figure 9 & Figure 10 show the electric field distributions of hexagonal and pentagonal platinum electrodes with bipolar potential for healthy and tumor tissues respectively. These bipotential distributions correlate very well with those using central positive electrode (and other electrodes at ground potential (0V). The average electric field magnitudes were 1230 and 1180V/cm respectively for hexagonal and pentagonal electrodes for both platinum and surgical steel electrodes. They match very well with the unipolar values of 1230 and 1180V/cm (Table 3). There is also good match for the maximum values of 2950V/cm for hexagonal and 2850V/cm for pentagonal electrodes. The results are same for surgical steel electrodes (data not shown).

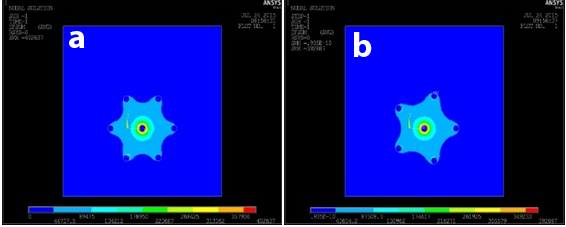
Figure 9 Electric field distribution using bipolar potential for healthy tissue using hexagonal (A) and pentagonal (B) Needle electrodes.

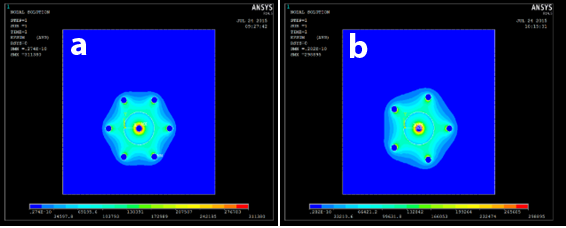
Figure 10 Electric field distribution using bipolar potential for tumor tissue using hexagonal (A) and pentagonal (B) Needle electrodes.

1. Electric field distribution was studied using ANSYS software that uses finite element technique, for hexagonal and pentagonal electrodes, made of platinum and surgical steel.
2. The average electric fields across tumor in case of platinum electrode are 1230 V/cm and 1180 V/cm (close to the desired magnitude of 1200V/cm) for both hexagonal and pentagonal electrodes, for both unipolar and bipotential voltages.
3. The electric field across tumor in case of surgical steel electrode is same as that of platinum.
4. The quantitative and graphical data for 2D electric field analysis of both platinum and surgical steel are similar and provide noticeable evidence that the choice of electrode material does not have much influence on the uniformity of electric field distribution as well as on the efficiency of electroporation. Thus selection of electrode material for electrochemotherapy could be for its chemical properties, physical properties and cost.
5. The correlation of bipotential electric field distribution with unipolar is useful, because it is much simpler to build bipotential pulse generators that unipolar pulsers.
6. These results are useful to transfer the technique from lab to clinics.

We gratefully thank Mr. Abdul-Qadir AR Buhari, Chairman, Dr. VM Periasamy, Vice Chancellor and Dr. V. Murugesan, Registrar of BS Abdur Rahman University, Chennai, India for their support and funding to accomplish this work.

The authors declare that there is no conflict of interest.

1. Salwa SP, Bourke MG, Forde PF, et al. Electrochemotherapy for the Treatment of Ocular Basal Cell Carcinoma; a Novel Adjunct in the Disease Management. J Plast Reconstr Aesthet Surg. 2014;67(3):403–406.
2. Jahangeer S, Forde P, Soden D, et al. Review of Current Thermal Ablation Treatment for Lung Cancer and the Potential of Electrochemotherapy as a Means for Treatment of Lung Tumours. Cancer treatment reviews. 2013;39(8):862–871.
3. Moller MG, Salwa S, Soden DM, et al. Electrochemotherapy as an Adjunct or Alternative to other Treatments for Unresectable or In-Transit Melanoma. Expert Rev Anticancer Ther. 2009;9(11):1611–1630.
4. Luca C, Simone M, Michela B, et al. Bleomycin Based Electrochemotherapy: Clinical Outcome from a Single Institution's Experience with 52 Patients. Annals of Surgical Oncology. 2009;16(1):191–199.
5. Mitchell W, Raji S. Electric Field Distribution in Biological Tissues for Various Electrode Configurations - A FEMLAB Study. Proceedings of the COMSOL Multiphysics User's Conference, Boston. 2005.
6. Gowri Sree V, Udayakumar K, Raji S. Electric Field Analysis of Breast Tumor Cells. International Journal of Breast Cancer. 2011:8.
7. Larkin JO, Collins CG, Aarons S, et al. Electrochemotherapy : Aspects of Preclinical Development and Early Clinical Experience. Ann Surg. 2007;245(3):469–479.
8. Soden DM, Larkin JO, Collins CG, et al. Successful Application of Targeted Electrochemotherapy using Novel Flexible Electrodes and Low Dose Bleomycin to Solid Tumours. Cancer Letters. 2006;232(2):300–310.
9. Corovic S, Pavlin M, Miklavcic D. Analytical and Numerical Quantification and Comparison of the Local Electric Field In The Tissue For Different Electrode Configurations. Biomed Eng Online. 2007;6:37.
10. Douglas H. Metal Corrosion in the Human Body. The Ultimate Bio-Corrosion Scenario. The Electrochemical Society’s Interface summer. 2008;17(2):31–34.
11. Tony N Stainless Steel for Hygienic Applications. European Confederation of Iron and Steel Industries.
12. Analytical Electrochemistry: Basic Concepts. Working Electrodes.
13. Kolpakova NA, Ageeva LD, Kovyrkina TV. Platinum Test In Biological Objects, Modern Level of Technical and Information Means Usage in Health Services. Proceedings of the VI International Scientific and Practical Conference of Students, Post-graduates and Young Scientists, Tomsk, Russia. 2000.
14. Sarah M, Richard G, Howard M. Platinum Neurotoxicity Pharmacogenetics. Mol Cancer Therapy. 2009;8(1):10–16.
15. Recommendation from the Scientific Committee on Occupational Exposure Limits for Platinum and Platinum compounds.
16. Mamdouh MS, Mohammed AE, Thannaa ES, et al. Studies on the Electric Field Distribution using Different Electrode Shapes For Electrochemotherapy. World Congress on Medical Physics and Biomedical Engineering.2009;25(10):252–255.
17. Kavitha S, Sadasivam P, Arun K, et al. Electrical Field Analysis of Pentagonal Needle Array Electrode for Electrochemotherapy Applications. 2012 Annual report Conference on Electrical Insulation and Dielectric Phenomena CEIDP. 2012:263–266.
18. GowriSree V, Udayakumar K, Raji S. Electric Field Mediated Inactivation of Tumor Cells. Electrostatics Joint Conference. 2009:16–18.