Purpose: To introduce and evaluate a fast-plugging pattern agent for the Gamma Knife treatment planning system (GKTPS) for potential clinical data retrospective analysis and educational application.

Methods and Materials: We developed an automatic plugging pattern generating system based on a greedy algorithm. This system is accessible from the Internet through a user-friendly interface. The input is based on the plan printout of the GKTPS using an extra simple contour information abstract method. This internet-based plugging pattern generator uses an updated algorithm to quickly generate plugging patterns for optimization of GK treatment plans for each individual shot and to sequence multiple-isocenter treatments.

Result: In 20 cases tested online, and the average computation time was about 30 seconds. This internet agent was also used in a Trigeminal Neuralgia treatment case.

Conclusion: This internet-based, fast plugging pattern GKTPS was able to quickly determine accurate dose distribution in different sites within the brain.

Keywords: gamma knife treatment planning, stereotactic radiosurgery (SRS), selective beam, plugging pattern

Gamma knife (GK) has been used to treat many different diseases, including brain tumors, skull base tumors, vascular abnormalities, functional problems, and ocular tumors.¹ Different tumors or disease sites involve complicated targets in crucial regions of the brain; therefore, it is challenging for the treatment planning system to meet the criteria of delivering more dose to the target while sparing critical structures or normal tissue so that the benefit to the patient is optimized. In GK treatment planning, the dose coverage of target is decomposed by the ellipsoid dose shape, which makes treatment plan optimization cumbersome. Due to the complexity of the Gamma knife treatment planning system and the variety of the treatment targets, it usually takes the clinician 45 minutes to 2 hours or more to achieve an optimal plan because of the various geometry setups and dose profiles generated by different shots, weights, sizes of collimator, blocking beam shaping, and the like.

A few optimization methodologies have been developed (7-16) based on different gamma knife simulation models.^2-6 There are generally two approaches for model simulation. The first is to simulate the overall effect of the 201 beam dose profiles,^4,5 which is essentially an empirical model using only weight, shot, and shot location. Another approach is to simulate each beam,^2,3,6 making it possible to select a single beam and to optimize the special treatment with an optimized plugging pattern. Since the gamma knife treatment plan can be influenced by different setups for each shot, the number of shots and shot locations, the weight of each shot, helmet size, helmet angle, blocking beams, and so on, the challenge is to use these parameters in combination to generate an optimal GK treatment plan. For example, a Guide evolutionary simulated annealing (GESA) algorithm has been used to generate shot packing plans for intracranial tumor treatment.⁷ Huazhong et al.⁸ presented a multiple penalty method in which sets of points in different regions of interest were selected based on point dose threshold conditions. For different parameters, such as the collimator size, different optimized algorithms included a conjugate direction searching method and a polynomial search. Wu et al.,⁹ applied the medial axis transformation method to generate a conformal dose plan for multiple-isocentric setups. Roger et al.,¹⁰ tried the sequential annealing-gradient optimization method by employing a least chi-square dose-matching function with differential weighting of tissues. Given any number of the shot locations and weights, a set of non-linear equations was formed. Solving the equations iteratively led to an optimal solution. Shepard et al.,¹¹ applied nonlinear programming techniques to optimize the gamma knife treatment plan by adjusting shot sizes, locations, and weight. Seungjong Oh¹² tried to decompose the target into sphere and cylinder dose distributions, but the edge of the real target was compromised. Deasy et al.,¹³ analyzed the deficiency of optimization with different objective functions. Yan et al.,¹⁴ and Luo et al.,¹⁵ applied the Powell’s method to solve the nonlinear equations. Leichtman¹⁶ suggested an adaptive simulated annealing algorithm to optimize the gamma knife treatment plan automatically.

Obviously, most of these optimization strategies involved generating an optimal plan by combining many parameters, including location of shot, size of collimator, number of shots weight of the shot, blocking beams, etc. However, a single parameter optimization strategy might simplify the optimization process and improve the treatment plan when the specific target is clear. Among these individual treatment options, selective beam blocking has been one of the preferred treatment methodologies. Selective beam blocking technique or plugging pattern GK treatment has been addressed using different approaches.^15,17-19 There are two selective beam blocking techniques. First, for small, irregular shaped target volumes, a single shot can be shaped to match the target by selective beam blocking. Second, in multiple iso-centric treatments, the abutment region between critical structures and the treatment target can be shaped to achieve better dose conformity to the target and to spare critical organs. Because of the large number of available blocking beam patterns, it is almost impossible to do an exhaustive search of all the possibilities.

There are 3 strategies for generating plugging patterns for a treatment plan. The first uses the planning software (Leksell GammaPlan, Elekta Instruments, Inc. Norcross, GA) to support a trial-and-error approach to customized plugging. The second is to apply the simulated annealing algorithm.^15,18 However, both methods are limited by time constraints. In a previously published study, a fast algorithm was developed to calculate the integral dose by combining target geometric information, dose distribution inside the volumetric target, and target location data.¹⁹ This method avoided the traditional exhaustive search and always selected the maximal dose contribution from different sources.¹⁹

In this paper, we updated the algorithm by optimizing the data for the gamma knife dose simulation model based on a greedy search approach and once were it available through the Internet, could provide a platform for a clinical evaluation tool to supplement the LGKTPS. To illustrate its use, a mimic Trigeminal Neuralgia case is presented in this paper.

This Gamma Knife plugging pattern treatment planning with the updated algorithm and application is internet based, providing free access for users seeking to test the effectiveness of their treatment planning. The algorithm application and test are carried on the server. It is potentially expandable to all other treatment planning systems, especially when the machine structure is standardized. In other words, the engine developed here can be employed in any small beam orientation and dose contribution optimization process. This application provides a simple interface with the Gamma Knife Treatment Planning System (GKTPS).

The result of the objective function in this application is integral dose, which is defined as:

Where I_i is the integral dose from the individual beam (which can be expressed as a dose function D_i (x, y, z)), N is the total number of beams selected to be blocked, and C_R is the critical structure or contour region. Resolving this equation allows for two approaches to integral dose calculation: 1) the integral dose can be computed by individual beam first or 2) for all beams collectively.

The objective function includes volume, dose, and geometry information, which enables values from multiple dimensions to be transferred to a single dimension; this distinguishes the algorithm for this internet agent from traditional multiple variable optimization algorithms. The core algorithm is implemented using a newly developed bucket-in-bucket structure index method to make the greedy algorithm possible. The greedy algorithm is an informed search strategy that enables each step of the search process to give deterministic results.²⁰

Design of internet agent structure

The procedure of designing the internet agent follows functional procedure programming methodology. Figure 1 shows the diagram of the internet website design strategy. Here, the agent function is illustrated by individual blocks that represent the web interface, data web entry, entry data consistency check, data processing and computation, and result internet display. Each block can also be further divided to represent different design strategies chosen from the procedure design method or the objective oriented design method.²¹

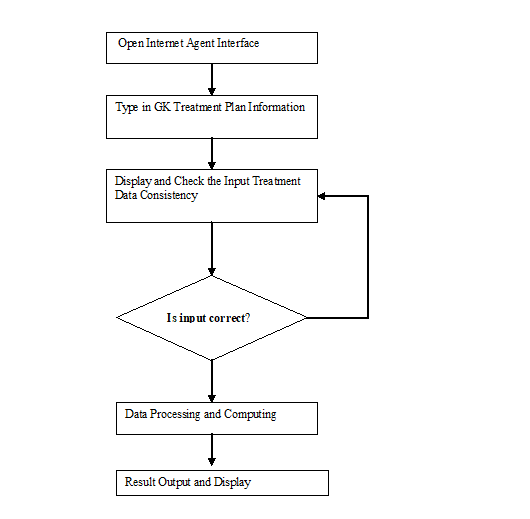
Figure 1 The flows chart to design the internet agent for gamma knife plugging pattern treatment planning.

Steps to implementing the internet agent

This internet agent is implemented in two steps

1. Calculation of Integral Dose (ID):

1. Either a pixel counting method, or the Monte Carlo method can be selected to calculate the ID. It can be used to integrate dose contributed by single beam, or combination of all beams. It is important that any point or voxel P_ijk be checked if it is inside the defined volume. There are different approaches to doing this. For example, we used a polygon boundary checking strategy. The detailed algorithm is addressed elsewhere.²² The optimization procedure includes both the optimal algorithm and the optimal data structure.
2. Once our target algorithm was selected, we updated the data structure to satisfy the requirements of the algorithm by generating an embedded bucket structure for storage of the beam dose contribution. Specifically, each bucket included information about the geometry of single beams, the index, and the dose contribution to the target. The dose and voxel location information were stored in a bucket-in–bucket format, or so called double-bucket structure (see figure 2).
3. With this data structure design, we simplified the best search approach procedure by index ordering, which sped up the arbitrary beam selection procedure. And the arbitrary beam selection procedure provided a very accurate selection for the dose distribution. For example, the voxel bucket at certain voxels included dose information, spatial information, and beam information (see Figure 2). The spatial information reflected the coordinates in gamma knife coordinate system. If the coordinate of the pixel bucket was transferred due to any coordinates system translation or rotation or switching between different types of the coordinate systems, all the bucket information within the voxel bucket was followed. The dose information revealed the dose at the spatial location.
4. Another bucket including beam information was used. In this beam bucket, the beam geometry information was described with j and q in a polar coordinate system.⁶ The dose described the contribution from certain beams at the spatial location defined by the upper-level bucket. The index provided a means of correlating the physical location to the treatment plan display, which was attached to the equipment itself, in this case, the Gamma Knife.

Figure 2 Illustration of bucket-in-bucket embedded structure inside a voxel.

2. Selecting the beam to be blocked

After the specially optimized bucket-in-bucket structure was designed, a fast search engine was implemented following the procedure described below.

1. Given the matrix center and shot center, the grid size, collimator size, and dose distribution of the matrix were calculated.
2. Given the dose from any point, pixel, or voxel the dose contribution from each beam was recorded in the voxel bucket.
3. Given the target contour, the integral dose to the target volume was calculated.
4. The integral dose contributions of the different beams were sorted according to the value of the integral dose.
5. Given the number of beams to be blocked, the beams were blocked based on their integral dose contribution to the target.
6. The blocking beam information was displayed based on the physical structure of the treatment machine.

3. Optional point dose verification function

We also included a module for point dose calculation and verification. Any point dose can be calculated using the following formula:

where the weight factor w_n includes the shot weight and the collimator factor. Given the arbitrary point (x_i, y_i, z_i) with dose D_Ti(x_i, y_i, z_i) and another point j at (x_j, y_j, z_j) and dose D_Tj(x_j, y_j, z_j), from the model, the ratio of the two points could be expressed as R_d, i.e., their relationship could be expressed as:

Description of input parameters

The implemented interface of the protocol is shown in figure 3.

Figure 3 A preliminary Web Engine interface.

The space for Patient Name was used to input a set of continuous characters without spaces. This "patient name" served as an identification to distinguish different calculations. The property of this field had no influence on the model calculation; however, it was used as an internal data processing identification device. GK Model selection included three models: 1 for model U, 2 for model C, and 3 for a possible other version such as Perfexion. The accuracy of the model was based on the dose profile from the Leskell Gamma Knife Treatment Planning System (LGKTPS). The specific method has been addressed elsewhere.^6,22 Skull Radius space included the average radius of the patient's skull. In LGKTPS, the radius was measured with a special bubble frame. Delta (Gamma) item was used for the delta angle for the U model and the gamma angle for the C model. The matrix center coordinate defined the actual location of the matrix, while the coordinates of the shots were referenced to the frame center at (100, 100, 100), and the required dose point can be calculated. The Grid Sizes ranged from 0.5mm to 2.5mm, which was also the same for the LGKTPS. There were 4 collimator size options: diameters of 4 mm, 8 mm, 14mm, or 18 mm at the isocenter. Given any known point dose with coordinate, for example, frame center dose at (100, 100, 100), then the calculation of the point dose was performed for any points of interest.

The number of blocking beams is important factor in that it allows the selection of an arbitrary number of beams. Doing this allows accurate dose analysis of the treatment planning. Because Gamma Knife has 201 beams, each beam contributes about 0.5% of the treatment dose at each shot if the attenuation difference is negligible. Due the complicated structure of the brain, accurate dose delivery is required; and arbitrary beam blocking is crucial to this process.

Target contour can get by using the point measurement function in LGKTPS to retrieve the coordinates of the points on the contour. Clicking on the contour allow several point coordinates on the contour to be read.

Because the time required for treatment planning was one of the important factors for blocking beam selection, we first tested our the internet treatment planning engine offline and found that it takes about 30 seconds to produce a plugging pattern. Different numbers of blocking beams had less effect on the length of computation time, and the internet setup had no significant effect on computational time.

Using this agent, we generated several patterns and calculated the dose to show the effectiveness of the web agent. By changing the number of blocking beams, we could demonstrate the effect on the DVH change. We used a trigeminal case setup as an example of a simple application of our internet plugging pattern treatment planning system. For simplicity's sake, only one critical region was considered (see Figure 4). This critical structure was drawn in only three slices. The coordinate of the contour can be read by the point dose measurement tool in LGKTPS, which is shown by the “+” symbol in left bottom corner image of figure 4. In this test example, the size of the critical structure was about 0.6 cubic centimeter. The complexity of volume computation and its variation need to be addressed in other publications. From this information and that describing the shots required (Figure 3), the blocking pattern was generated with the pre-set number of blocking beams. The display of plugging beam was based on the fix configuration of gamma knife system through indexing method and accomplished in excel spread sheet.

Figure 4 To define the Critical Structure for a mimic Trigeminal Neuralgia case with only 3 axial images.

Figure 5 shows the plugging pattern generated with different numbers of selective beams. As one can see, the blocking beams are expanded around pattern following their integral dose contribution to the critical structure. Unlike a simulated annealing algorithm, each iteration of which could possibly generate a different pattern of blocking beams, our internet agent always gives a single optimal solution for a given treatment setup and target information. In figure 5, plugging patterns with 5, 10, 20, 30 and 50 beams blocked are shown for the C model Gamma Knife. The effectiveness of the blocking pattern treatment is evaluated by two conventional criteria. The first is the isodose line that provides the visualized dose distribution. Figure 6 shows the target isodose line in axial, sagittal, coronal views with different numbers of blocking beams; a significant isodose line change is seen on the coronal cut. The 20% isodose line has moved entirely outside of the target. However, the sagittal view shows that the 20% isodose line covers more of the target, which implies that the visual image alone is inadequate to evaluate the treatment planning. Therefore, a different quantitative evaluation parameter is needed to help clinicians to evaluate different treatment plans. The series of images in this figure also illustrates the complexity of the treatment planning in radiosurgery; an improved tool is needed to provide clinicians with a better solution. In this beam-blocking treatment, the objective function of the integral dose is sensitive to the plugging pattern and, therefore, could generate an optimal plan.

Figure 5 Plugging patterns generated by Internet Agent with 5, 10, 20, 30, 50 and 60 blocking beams, respectively.

Figure 6 Iso-dose lines shows the dose distribution in axial (left), sagittal (mid) and coronal (right) views for 0, 20, 30, and 50 blocking beams, respectively.

To show the sensitivity of this plugging pattern treatment planning, we analyzed the dose volume histogram of the critical structure. Figure 7 illustrates the DVH curves of a set of treatment plans ranging from no plugging pattern to blocking 60 beams. The DVH shows a non-linear change in the dose sparing effect. The DVH curves are shown in a linear scale (upper figure) and a logarithmic scale (lower figure) to further describe the blocking effect. When even just 5 beams are blocked, the difference between the DVH curves is pronounced. When SRS is used to treat benign tumors (i.e., treating a small target with a high dose), a small increase in the dose to critical structures could possibly generate unexpected complications. A careful selection of a few beams to block can provide better patient care. And since it is usually difficult to distinguish a small percentage of difference in dose distribution by viewing the isodose lines on the treatment planning system, a better quantitative measure is needed for better treatment planning. This kind of accuracy might also be very useful in evaluating blocking patterns in trigeminal neuralgia treatment.²³

Figure 7 DVH generated with different number of plugs.

Another approach to determining the number of blocking beams is to analyze the DVH by picking the same volume point and same dose point. Figure 8 shows that the dose and volume vary with the number of plugs. As the number of blocking beams increases to 30 or 40, the dose to the target volume decreases. However, this changes as the number increases to 50 or 60, which means the dose contribution of single beam to critical region has similar effect that cause DVH curves to change at the minimum volume and large dose gradient region. This phenomenon suggests that, in the conformal GK treatment, the number of beams that are blocked may be about 30 to 40. Increasing the number of blocking beams beyond this will require very careful evaluation of the dose distribution of the treatment plan.

Figure 8 The relative volume of critical structure covered by different iso-dose lines, 20% (blue-square curve) and 50% (yellow-square curve), and the relative dose covering 20% (red-diamond curve) and 50% (green-diamond curve) of target volume, as a function of the number of blocks.

By applying several optimization structures to a greedy algorithm approach, a feasible internet agent supplemental to the gamma knife plugging pattern treatment planning was created. We redefined the optimization treatment planning for data structure and programming simplification and tested this internet engine with a trigeminal neuralgia case. The results showed that the sensitivity of the plugging pattern to the target was dependent on the location of the shot(s) and the number of plugging beams. With the integral dose as a non-linear objective function, the internet agent was efficient and effective.

Currently the computational processing of the internet agent is limited to only one target. Multiple target analysis can be achieved using a merge strategy, and further research is continuing the effect of variation of targets, analysis of clinical data, labor issues in treatment planning, combination of other evaluation parameters or tools, computational issues for high gradient dose distribution, and other complicated treatments.

The limitation of this development was only for fixed configuration Gamma Knife System. Further expansion could be applied to other cone-based radiotherapy systems given their flexibility of spatial allocations of beams. As addressed above, in this clinical application development, the cord optimization objective function was integral dose, and the enlightenment of the integral dose could be further explored with the characteristics of different target volume such as size, location, and so on.

Theoretically, given fixed number of multiple targets and beam configuration, there could be a single optimal solution, which is analogical to the unique solution of linear equation. And the future studies could combine with different clinical objectives. Moreover, this development showed some initial hints in mathematical aspects.

In conclusion, for this development and clinical application study, a simple dimensional conversion greedy algorithm was invented and applied in a gamma knife system, and its efficacy was implemented by lowering the complexity of beam selection radiotherapy planning procedure.

None.

Author declares that there is no conflict of interest.

1. Lunsford LD, Kondziolka D, Flickinger JC, editors. Gmma Knife Brain Surgery, progress in Neurological Surgery. Volume 14. Switzerland: Karger; 1998.
2.  Zhang P, Dean D, Wu QJ, et al. Fast verification of Gamma Knife treatment plan. Journal of Applied Clinical Medical Physics. 2000;1(4):158‒164.
3.  Marcu SM, Wu QJ, Pillai K, et al. Gamma Plan-Leksell Gamma Knife Radiosurgery Treatment planning verification method. Med Phys. 2000;27(9):2146‒2149.
4. Tsai J, Engler MJ, Rivard MJ, et al. A formalism for independent checking of Gamma Knife dose Calculation. Med Phys. 2001;28(9):1842‒1849.
5. Phaisangittisakul N, Ma L. An empirical model for independent dose verification of the Gamma Knife treatment planning. Med Phys. 2002;29(9):1991‒1997.
6.  Li K, Ma L. Selective source blocking for Gamma Knife radio surgery of trigeminal neuralgia based on analytical dose modeling. Phys Med Biol. 2004;49(15):3455‒3463.
7. Zhang P, Dean D, Andrew M, et al. Optimization of Gamma Knife treatment planning via guide evolutionary simulated annealing. Med Phys. 2001;28(8):1746‒1752.
8. Shu H, Yan Y, Luo L, et al. Three-dimensional optimization of treatment planning for gamma unit treatment system. Med Phys. 1998;25(12):2352‒2357.
9.  Wu QJ, Bourland JD. Morphology-guided radio surgery treatment planning and optimization for multiple isocenters. Med Phys. 1999;26(10):2151‒2160.
10. Ove R, Popple R. Sequential annealing-gradient Gamma-knife radio surgery optimization. Phys Med Biol. 2003;48(14):2071‒2080.
11. Shepard DM, Ferris MC, Ove R, et al. Inverse treatment planning for Gamma knife radio surgery. Med Phys. 2000;27(12):2748‒2756.
12.  Oh S, Suh TS, Song JY, et al. Development of a rapid planning technique based on heuristic target shaping for stereotactic radiosurgery. Med Phys. 2004;31(2):175‒182.
13. Deasy JO. Multiple local minima in radiotherapy optimization problem with dose-volume constraints. Med Phys.1997;24(7):1157‒1161.
14.  Yan Y, Shu H, Bao X, et al. Clinical treatment planning optimization by Powell’s method for Gamma unit treatment system. Int J Radiat Oncol Biol Phys. 1997;39(1):247‒254.
15. Luo L, Shu H, Yu W, et al. Optimizing computerized treatment planning for the Gamma Knife by source culling. Int J Radiat Oncol Biol Phys.1999;45(5):1339‒1346.
16. Leichtman GS, Aita AL, Goldman HW. Automated Gamma Knife dose planning using polygon clipping and adaptive simulated annealing. Med Phys. 2000;27(1):154‒162.
17. Flickinger JC, Maitz A, Kaiend A, et al. Treatment volume shaping with selective beam blocking using the Leksell Gamma Unit. Int J Radiation Oncology Biol Phys. 1990;19(3):783‒789.
18. Zhang P, Wu QJ, Dean D, et al. Plug pattern optimization for Gamma Knife Radio surgery treatment planning. Int J Radiation Oncology Biol Phys. 2003;55(2):420‒427.
19. Schlesinger D, Snell J, Sheehan J. Shielding strategies for Gamma Knife surgery of pituitary adenomas. J Neurosurg. 2006;105 Suppl:241‒248.
20. Russell S, Norvig P. Artificial Intelligence a modern approach. Second Edition. Prentice Hall; 2003.
21. Pressman RS. Software engineering a practitioner’s approach. 4th Edition. The McGraw-Hill Companies, Inc.; 1997.
22. Li K, et al. Monte Carlo Computation of Integral Dose. (In preparing).
23. Massager N, Nissim O, Murata N, et al. Effect of beam channel plugging on the outcome of Gamma Knife radio surgery for trigeminal neuralgia. Int J Radiation Oncology Biol Phys. 2006;65(4):1200‒1205.