Shape is one of the oldest and constantly employed descriptors of species morphology. In the era of molecular identification and species characterization tools, shape is in the focus of new interdisciplinary efforts in search of better describing and understanding phenotypical niche, morphological spaces and the information they can convey. Fungi are morphologically versatile organisms, with different shapes corresponding to different stages in their life cycles, resource capture versus reproduction and dispersal strategies, presenting different topologies. In this review, different methods employed in fungal shape analysis from fractals, Lindenmayer systems, networks to geometric morphometrics and machine learning were presented. However, fungal shapes pertain mostly to hyperbolic and spherical geometries not investigated to the moment and worth to approach in the future.

Keywords: fungi, shape, geometric morphometrics, fractals, phenotypical niche, hyperbolic space

In the era of molecular tools used in description and identifications of organisms, their shape still can convey a lot of important information on their properties, identity, evolution and interactions with environment. The almost-compulsory condition to provide molecular identification in most of the studies dealing with biodiversity, description of new species, the great hopes that bar coding will increase the accuracy of species inventories in various environments¹ are hindered by expensive techniques and the fact that the assignment of organisms to taxonomic categories relies on highly incomplete data bases: some taxa are better known merrily due economic interest behind the acquired knowledge, other taxa are almost ignored.

Morphology dealing with structural appearance of the organisms evolved to more sophisticated and integrative sub-disciplines connecting the appearance to physiology, phylogeny, genetics, and ecology. A new field of eco-morphology interconnects knowledge on adaptive physiological mechanisms targeting the fitness of an organism, ecological niche, and morphology.² Shape is one of the oldest and yet among most reliable descriptors for species or more generally, item recognition. Particularly, concerning living entities, shape is a large scale expression of many organizing, competing and highly regulated biological processes. Shape mirrors environmental constraints and can be analyzed independently from size. When it is combined with dimension, the resulting entity is referred as form. More formally, shape and form are components of the phenotypical hypervolume (Figure 1) which is in turn a component of ecological niche hypervolume.³ In the context of geometric morphometrics, for instance, shape was redefined as the geometric property of a configuration of points which remained unchanged after translation, rotation and scaling.^4,5

Why shape is still so important? Shape is a category of valuable descriptors which can be quantified and used in species discrimination based on some hidden differences revealed by geometric morphometrics, fractals, L systems or graph theory. Basically, shape can be encoded in a sequence of numbers establishing a high dimensional vector, each specimen described in these terms occupying a point in the specimen (cell)-shape space with some statistical characteristics. It is the place to remind a fundamental truth that pure biology is the study of patterns in nature similar to pure mathematics dealing with patterns of numbers.⁶ The symbiosis between mathematics and shape space lead to morphological spaces or morphospaces which are mathematical spaces describing and relating the phenotypic configuration of organisms.⁷

Shape in fungi has been analyzed at different scales: from subcellular, cellular, whole mycelia, colonies, to ascocarps and basidiocarps, ranging from microns to meters. Much attention was paid to mycelia, colony shapes and spores but macroscopic structures such as ascocarps or basidiocarps were not tackled and their shape description remained at the level of metaphoric similarities. Different types of geometry characterize mycelia and reproductive/dispersion structures or populations of lesions developed on plant surfaces.

A critical moment in shape analysis is image acquisition especially when it comes to microscopic structures. From camera lucida drawings to software toolboxes devised for semi-automatic, automatic or manual image acquisition, this field has experienced huge leaps forward. For instance one of the latest software, HyphaTracker: An ImageJ toolbox was devised to capture spore germination and hyphal extension incorporating time as additional variable.⁸ Previous work on automated image analysis used in the assessment of various size and shape parameters in filamentous fungi were reviewed by Papagianni.⁹

An array of methods borrowed from mathematics and computer science has emerged during the last decades. Multivariate morphometrics, geometric morphometrics, fractals, Lindenmayer systems, networks, machine learning, and pattern recognition all being employed to make shape analysis quantitative. Multivariate statistics is still used to extract phenotypic information from size variables. Machine or computer vision systems recognize shape, color, texture of objects under study and provide numerical attributes which can be subjected to further analysis.¹⁰ A fractal is a rough, fragmented geometric shape that can be subdivided in parts, each of which is (at least approximately) a reduced/size copy of the whole.¹¹ Natural fractals pertain to branching systems from rivers to mycelia, ferns, trees; bifurcation and self-similarity are fundamental properties of fractals. A special case of complex fractals are Lindenmayer systems which are string rewriting mechanisms introduced to model the development of organisms which permit also to produce realistic images of the objects. An L-system consists of a finite set of symbols (alphabet), a start symbol or string of symbols (axiom) and a finite set of rules (productions). A network is a catalog of system’s components called nodes and links or edges, containing map of its wiring diagram. Any complex system whose components interact can be assimilated to a network (in mathematical parlance, graph) and specific attributes or metrics can be employed in order to find its latent properties.¹²

Geometric morphometrics initiated by D’Arcy Thompson (his seminal book on growth and form celebrated a century from the issue in 2017) studies the variation and covariation of shape descriptors together with influential environmental factors. The advent of coordinate based methods and outline analysis using different approaches, basically fitting functions to characterize the closed or opened curves depicting different organisms or parts of organisms represented a major revolution in morphometry.⁷ Since 1980 major advances were made in the field of geometric morphometrics, the subfield of statistics interested in shape quantification. Generally, traditional morphometry based on measurements is combined with geometric morphometrics to create a more powerful model.

Geometric morphometrics combine geometry, multivariate morphometrics, computer science and various imaging techniques from very simple photographs to automated and standardized mapping of the surfaces of organisms or organs. GM techniques has greatly enhanced the ability to discriminate taxa using 2d and 3D modelling of organisms’ morphology and to analyze separately 3 main components of biological form: size, shape and symmetry. It permits an objective interpretation of minor morphological variation. Numerical representations of shape (sometimes including form) rely on coordinate data, boundary data and textural aspects. For outline or boundaries, one of the most frequently employed category of methods rely on Fourier series, on Fourier transforms more specific, which is the mapping from spatial domain (the morphological domain) into the frequency domain composed of new variables such as amplitudes, for instance. The largely employed Elliptic Fourier Analysis (EFA), resolves global aspects of shape but not the localized features for which wavelet analysis is devised. This approach provides an objective procedure to identify localized features as changes in curvature along a biological form.¹³ Closely related Eigen Shape Analysis (ESA), is a technique used for the reduction of digitized outline shapes into few parameters for multivariate analysis (Principal Component Analysis, Multivariate Analysis of Variance, Discriminant Analysis, etc.) and visualization of shape variation.¹⁴⁻¹⁶ The coordinate points collected from the outline are converted in angles and in phi function. The entire curve is interpolated in standard ESA in equally spaced points which become the comparison basis across specimens.¹⁷ In EFA and ESA the location of each point in the boundary outline sequence is dependent on the location of the previous point.⁶

Landmark or coordinate data define a map between any two surfaces that is as close as possible to an isometry. Sets of landmarks are chosen on compared shapes that must obey to homology criteria, should conserve their relative position, and should be found constantly in all specimens. Semi-landmarks on the other hand are regularly spaced points which can be set on the outline of shape as well. Shape information is extracted from the position of the landmarks, the extraneous variation due to size, position and orientation being removed in a procedure called the Procrustes superimposition. The coordinates of landmarks aligned by this procedure contain the information on shape variation.¹⁸ As shape variation is multidimensional, the analyses pertain to multivariate statistics that simultaneously consider covariation of landmark coordinates such as Principle Component Analysis, Multivariate Regression, Canonical Variate Analysis, Partial Least Squares Analysis. Algorithms are employed to permit shape changes visualization by relative shifts of the landmarks and by deformation of outlines. However, these methods are based on the reduction of morphologies to some features considered relevant and discriminatory such as outlines or selected homologous landmarks.⁶

The next level in the analysis of shape is machine learning which is the direct analysis of digital images or scans in 2D or 3D of sets of objects. The use of pixel brightness and color values as subjects of morphometric investigation makes more operational the GM standard approach by extending the analysis to all points composing the investigated object.⁶ Confusion matrices are constructed and group partition is performed using logistic regression.

The evolution of GM and related shape analysis algorithms are in certain regards, over simplifications, the current recommendation being to perform several types of analyses on the same set of objects and to assemble the results.⁶

Fungi display an astonishing diversity of morphologies and the capacity to switch to different modes of appearance, being in other words, highly pleomorphic. Morphologies accommodate different strategies in resource capture, dispersal, spatial exploration, interactions with other species, and among most important, symbiotic interactions. It was observed that changes in shape and/ or dimension were required in disease microbes to become successful pathogens. Dimorphic fungi switch from filamentous growth to yeast like, which is a morphotype transition characterizing pathogenic life style.¹⁹

Any morphometric approach relies on image capture which developed to recent array of diverse digital image analyses based on computer vision, a technology that can extract useful information by processing and manipulating images in a computer.²⁰ Images refer to hyphae, mycelia, spores when microscopic level structures are investigated or colonies, mycelial chords or strands, sporophores when macroscopic structures are envisaged. Software was developed to analyze images either microscopic or macroscopic photographs. ImageJ, Image Tool²¹ or specialized packages in R.²

Size is an important and a long history type of morphological character conveying information on species differences and adaptations. For instance, in Polyporales and Agaricalesore size is positively correlated with basidiocarp size^22,23 it was stated that small spores are adapted for effective wind dispersal and larger spores can provide more nutrients and ability to overcome hostile environment. Apparently, in Polyporales, spores represent a compromise between dispersal and survival as the common size of these spores is around 10μm²⁴.

Pathogenic fungi and fungi like organisms are embedded in hosts’ tissues. A large category of shape studies focused on symptoms and populations of lesions produced by plant pathogenic fungi; pathogen identification was subsequently based on the specific morphology of lesions. Pathogenic fungi and fungi like organisms adapt largely their shape to characteristics of host targeted tissues, to specific patho-system attributes (such as virulence, aggressivity) and life cycle, lesions being the expression of pathogen-host interaction, in many cases of high morphological specificity. Many disease detection and characterization systems using computer vision developed for spatially defined lesions and symptoms on leaves; spots or necrotic areas produced by mildews, rusts, anthracoses, tar spots, etc.^25,26, development of colonies on seeds and fruits.²⁷ Wavelet feature extraction was also employed as tool for image analysis in disease assessment.²⁸

Computer vision was employed as main tool for detection and visualization symptoms of plant diseases from color image, the extracted features being used afterwards as inputs to various classifiers such as Support Vector Machine Classifier²⁹ or K-nearest neighbor classifier.³⁰ Machine vision systems can employ camera and visible light, polarized light or can be performed using X ray or nuclear magnetic resonance, multispectral imaging (consists in a set of several images, each acquisition at a narrow band of wavelengths)²⁷ or hyperspectral imaging³¹ combining the features of images and spectroscopy to acquire both spatial and spectral information of the object of interest.¹⁰

Shape of colonies have been a category of descriptors widely used in species identification, study of physiological or biochemical features and formalized approach coming from image analysis combined with unsupervised and supervised classification³² to geometric morphometrics or fractals produced new quantitative information used in phylogenetics or eco-morphology. EFA was used for the quantification of changing yeast colony morphology with time³³, yeast being grown on standard solid media.

Lindenmayer systems were also employed in the study of colony shapes.³⁴ For instance, on simulated images colony morphology of filamentous fungi appeared to be determined by different types of branching angles. Circular shapes arise from statistical variation of hyphal extension rate, internode length and branching angle size.³⁴

Mitotic and meiotic spores are in the microscopic size range but their shape varies greatly. It is considered that cell shape in microbes (fungal spores included) is the expression of many organizing competing and highly regulated biological processes and interactions.³⁵ If spores are in focus, this approach permits to statistically distinguish populations^35,36 using tools of GM’s semilandmarks or outline analysis. Another approach is of the category L systems applied for instance to describe the conidiogenesis in Alternaria sp.³⁷

Fungal mycelium displays exploration/exploitation growth strategies; it pertains to the category of branching fractals. The bifurcation of hyphae during extension is a fundamental behaviour of the fractal. Fractals are objective and scale independent measures of shape and complexity. In a larger context, the architecture of mycelia varies as function of the characteristics of substrata. It spreads and branches differently on solid substrata and submerged in liquid media. Moreover, in pathogenic fungi, mycelia are highly pleomorphic switching from filamentous growth to yeast like. Many studies have targeted the fractal pattern of mycelia.³⁸⁻⁴⁵ Fractals accommodate branching structures such as mycelia of fungi and filamentous fungi-like organisms as Oomycota or plasmodia of slime molds (Myxomycota) and capture as a metric mycelial complexity at microscopic level or macroscopic in case of chord forming mycelia remaining a summary statistic. However, important information can be extracted or inferred from fractal variation of shape; in lichenized fungi it was observed that increased branching measured by fractal dimension corresponds to increased capacity to harvest water from fog.⁴⁶ Also, differences were assessed in terms of fractal dimension of normal and virus infected mycelia of the aggressive pathogen Cryphonectria parasitica.⁴⁰

Another direction in approaching mycelia comes from network theory; nodes are placed at the points of branching and links are represented by hyphae between two branching points. As mycelia forage in heterogeneous substrates, they form complex networks which can be analyzed with tools provided by graph theory on digital images obtained from mycelia grown under realistic conditions.⁴⁷ Mycelial networks progress from a centre in radial manner changing topology from branching network trees to lattices due to extended interconnections.⁴⁸ This topological shift as mycelial foraging and growth progress can be quantified using planar graphs metrics such as meshedness or alpha index and shortest paths. It shows how mycelium of Phanerochaete velutina progresses from alpha index of 0 to a level of interconnectedness of 10-20%,⁴⁸ a phenomenon linked to transportation efficiency and foraging strategies. EFA was used for the classification of shapes of conidia in Ascochyta lentis.⁴⁹ Basidiocarp shape analysis: EFA was employed to assess variation of basidiocarp shapes of Trametes versicolor.³⁹

Shape encompasses properties tied to niche of an organism and adaptations appeared as response to environmental challenges. However, in the case of spore shape and sporophore extraordinary diversity of shapes there is little quantitative explanations, most of it being highly hypothetical.⁵⁰

GM exploring the complexity of biological objects in 2D and 3D constructs morphospaces which are based on Euclidean tangent space to Kendall’s shape space (which is spherical) meaning that all envisaged shapes are constrained to Euclidean space rules.⁷ Since the vast majority of organisms fungi included present non-Euclidean geometric features GM is somehow reductionist. Spherical or elliptical and hyperbolic geometries have different properties, as for instance, distance which is defined differently (in hyperbolic plane the shortest path between two points is a curve which is longer than a line in Euclidean plane).⁵¹ Accordingly, these geometries reflect adaptive growth strategies, reconsider boundary dependent processes.

The fractal or graph like structure of mycelia adapted for optimal transportation of nutrients or metabolism products within hyphae is embedded in a substrate or on/in an organism. The geometry of the embedding surface is important: as studies were performed on mycelia developing under isotropic conditions on an Euclidian surface such a solid media in Petri plates or on cellophane membranes, in nature these surfaces can display different topologies. The leaf is approximated by 2D surface but it is seldom Euclidean like: the upper surface of the broadleaved tree leaves is curved and corresponds to a hyperbolic surface. By consequence several properties of the Euclidean space do not hold.

Mycelia of ectotrophic powdery mildews such as Erysiphe alphitoides on leaves of Quercus spp. develop on the upper surface and the branching features (frequent anastomoses and branching at right angles) are different from other types of mycelia exploring for instance, soil. There must be a correlation between the curvature of the leaf, leaf microtopography and the geometry of the mycelia apart from other leaf local characteristics such as position of the stomata, presence of hairs or the thickness of the cuticula.

Hyperbolic geometry deals with surfaces with negative curvature. For instance, the analysis of the outlines of bracket fungi such as Trametes versicolor or the boundary of foliose lichens do not portray accurately the shape complexity since these structures display hyperbolic surfaces. Trametes versicolor shape variation analysed with respect to contour descriptors reveal an average, fundamental shape. However, the surface presents negative curvature, it is a hyperbolic surface. Apothecia are hyperbolic, saddle shaped surfaces. Hyperbolic surfaces are encountered from molecular self-assembled lipid layers in the cells⁵² to leaves, basidiocarps of such species as Trametes versicolor, Tremella mesenterica, Sparassis crispa, to corals, marine snails and many other organisms.

 For the time being, projections of complex and folded structures on hyperbolic plane were performed for human brain scans, comparison of fossil primate skulls and protein folding using the software Match Surface. Other methods used in human medical research rely on surface parameterization using Ricci flow method (explores curvature under the topology of different manifolds), with projection of one of standard models of hyperbolic planes as Poincaré disk and Klein model endowed with hyperbolic metric.⁵³ As topology of many anatomical features is of higher order genus, novel approaches borrowed from differential geometry explore the possibility to map these entities onto hyperbolic space. A combination of landmarks and projections of the targeted high genus surfaces in hyperbolic plane combined with minimal surfaces was used to compare ear vestibular organs in healthy and impaired individuals.⁵⁴ In topological classification of surfaces, the genus refers to the number of cuts needed to make on the plane in order to reduce it to a sphere with holes. Minimal surface is a surface that presents constraints that minimize it; examples are the catenoid and the helicoid, both shapes largely encountered in nature. It is worth to mention that high genus or convoluted structures emerge also in fungi: morels, internal structure of Tuber spp., truffles’ sporophore, hymenophore structure in mushrooms, jelly fungi (Tremella spp.) and many others.

Other non-Euclidean surfaces are spherical explored also more in medical literature. Spherical geometry with positive Gaussian curvature characterizes for instance the shape of sporophores of hypogeous fungi, chasmothecia of Erysiphales (powdery mildews), many types of mitotic or meiotic spores, etc.

As the next level in taxonomy will be the automated species identification using technologies such as pattern recognition (using geometric morphometrics array of techniques), machine learning and artificial intelligence,^{1, 55} more people, scientists not necessarily trained in taxonomy will be able to provide species’ inventories. Automated identification systems are currently used for the identification of insects, Daisy (Digital automated Identification System)⁵⁶, bees (Automatic Bee Identification System-ABIS)⁵⁷ or microbial populations (automatic Identification and Characterization of Microbial Populations – AIMS).⁵⁸ The bewildering diversity of fungal shapes makes this task very challenging, however extremely necessary for future developments in fungal biodiversity studies, in eco-morphology or practical topic as biotechnologies, bioremediation.

Shape is still concentrating important clues for the understanding of species diversity and niche, adaptations, positions within communities, properties and interactions with each other and with environment. We expect future spectacular developments in shape assessment methods paralleling huge technological and knowledge progresses.

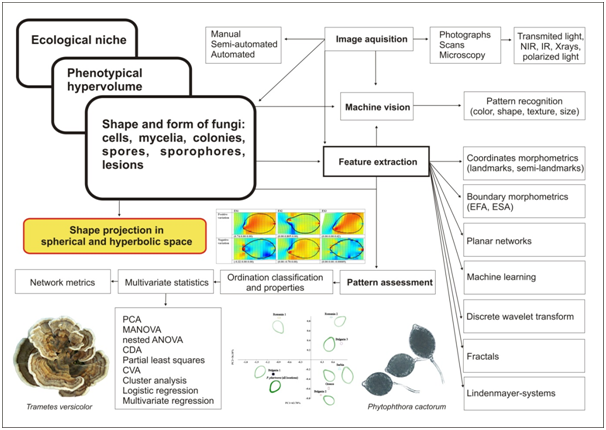
Figure 1 Chart showing the position of fungal shape within ecological niche hypervolume and the present state of art in shape analysis applied to fungi. Possible future directions – non-Euclidean geometry (spherical and hyperbolic spaces). PCA, principal component analysis; MANOVA, multivariate analysis of variance; CDA, canonical discriminat analysis; CVA, canonical variate analysis; ANOVA, analysis of variance; ESA, eigenshape analysis; EFA, elliptic fourier analysis; IR, infrared light; NIR, near infrared light

There is no conflicts to publish our article in this Journal.

1. McLeod N, Benfield M, Culverhouse P. Time to automate identification. Nature. 2010;467:154−155.
2. Betz O. Ecomorphology: Integration of form, function, and ecology in the analysis of morphological structures. Mitt Dtsch Ges Allg Angew Ent. 2006;15:409−416.
3. Blonder B, Lamanna C, Violle C, et al. The n-dimensional hypervolume. Global Ecology and Biogeography. 2014;23(3):595–609.
4. Kendall DG. A survey of the statistical theory of shape. Statistical Science. 1989;4(2):87−120.
5. Slice DE, Bookstein FL, Marcus LF, et al. A Glossary of Morphometrics. In: Marcus LF, Corti M, editors. Advances in Morphometrics. 1st ed. Plenum Press, New York; 1996: 531−551.
6. McLeod N. On the use of machine learning in morphometric analysis. In: Lestrel PE, editor. Biological shape analysis. Proceedings of the 4thInternational Biological Shape Symposium. World Scientific Co. Pte. Ltd. Singapore; 2017: 134-171.
7. Mitteroecker P, Huttegger S. The concept of morphospaces in evolutionary and developmental biology: mathematics and metaphors. Biological Theory. 2009;4(1):54−67.
8. Brunk M, Sputh S, Doose S, et al. HyphaTracker: an ImageJ toolbox for time-resolved analysis of spore germination in filamentous fungi. Sci Rep. 2018;8(1):615.
9. Papagianni M. Characterization of Fungal Morphology using Digital Image Analysis Techniques. J Microb Biochem Technol. 2014;6:189–194.
10. Chen KR, Chao K, Kim MS. Machine vision technology for agricultural applications. Computers and Electronics in Agriculture. 2002;36:173–191.
11. Mandelbrot B. The Fractal Geometry of Nature. WH Freeman Co., NY; 1982.
12. Barabási AL. Network Science. Cambridge University Press. Cambridge CBZ 8BS, UK; 2016.
13. Lestrel PE. From elliptical fourier functions to wavelets: three decades of boundary morphometrics. In: Lestrel PE, editor, Biological shape analysis. Proceedings of the 4th International Biological Shape Symposium. World Scientific Co. Pte. Ltd. Singapore; 2017:172–214.
14. Lohman GP. Eigenshape analysis of microfossils. A morphometric method for describing changes in shape. Mathematical Geology. 1983;15:659–672.
15. McLeod N. Shape Theory. Paleontological Association Newsletter. 2009;71:34–47.
16. Ray TS. Landmark eigenshape analysis: homologous contours, leaf shape in Syngonium (Araceae). Am J Bot. 1992;79:69–76.
17. McLeod N. Going round the bend: eigenshape analysis I. Paleontological Association Newsletter. 2012;80:35–45.
18. Klingerberg CP. Evolution and development of shape: integrating quantitative approaches. Nat Rev Genet. 2010;11(9):623–635.
19. Wang L, Lin X. Morphogenesis in fungal pathogenicity: shape, size, and surface. PLoS Pathog. 2012;8(12):e1003027.
20. Oliveira da Silva FO, Itako AT, Tolentino JB. Mycelial growth assessment by digital image analysis in R software environment. Idesia. 2017;35(1):5–8.
21. Wilcox CD, Brent S, Dove W, et al. Image Tool version 3.0, San Antonio, TX; 2002.
22. Kauserud H, Heegaard E, Halvorsen R, et al. Relationship between basidiospore size, shape and life history characteristics: a comparison of polypores. Fungal Ecology. 2008;1(1):19–23.
23. Meerts P. The evolution of spore size in Agarics: do big mushrooms have big spores. Journal of Evolutionary Biology. 1999;12(1):161–165.
24. Gregory PH. Fungus spores. Transactions of British Mycological Society. 1952;35:1-18.
25. Fodor E, Teuşdea A. Image analysis employed for the estimation of the foliar areas affected by tar spots - Rhytisma acerinum (Pers.)Fr. in maples (in Romanian). Rev Păd. 2002;117(5):24–28.
26. Pujari JD, Yakkundimath R, Byadgi AS. Image processing based detection of fungal diseases in plants. Science Direct. Procedia Computer Science. 2015;46:1801–1808.
27. Jørgensen JR, Carstensen JM, Søren K, et al. Identification of barley grain mycoflora by next generation sequencing and videometer multispectral imaging. Abstract from ICNIRS 18th International Conference on Near Infrared Spectroscopy, København, Denmark; 2017.
28. Pujari JD, Yakkundimath R, Byadgi AS. Automatic fungal disease detection based on wavelet feature extraction and PCA analysis in commercial crops. I.J. Image, Graphics and Signal Processing. 2014b;1:24–31.
29. Camargo A, Smith JS. Image pattern classification for the identification of disease causing agents in plants. Computers and Electronics in Agriculture. 2009;66(2):121–125.
30. Pujari JD, Yakkundimath R, Byadgi AS. Neuro-kNN classification systems for detecting fungal disease on vegetable crops. Agric Eng Int: CIGR Journal. 2014a;16(4):299–308.
31. Erskinbaev C, Morrison J, Paliwal J. A novel exploratory shape analysis method to identify spatial variation of fungal infection level on wheat kernels. In: Lestrel PE, editor. Biological shape analysis. Proceedings of the 4thInternational Biological Shape Symposium. World Scientific Co. Pte. Ltd. Singapore; 2017: 71–79.
32. Dörge T1, Carstensen JM, Frisvad JC. Direct identification of pure Penicillium species using image analysis. J Microbiol Methods. 2000;41(2):121–133.
33. Gil de Prado E, Rivas EM, de Silóniz MI, et al. Quantitative analysis of morphological changes in yeast colonies growing on solid medium: the eccentricity and Fourier indices. Yeast. 2014;31(11):431–440.
34. Soddell F, Seviour R, Soddel J. Using Lindenmayer systems to investigate how filamentous fungi may produce round colonies. In: Stonier Yu, editor. Complex systems. Mechanisms of adaptation. IOS Press, Amsterdam; 1994: 61–66.
35. Pincus Z, Theriot JA. Comparison of quantitative methods for cell-shape analysis. Journal of Microscopy. 2007;227(2):140–156.
36. Fodor E, Hâruța O, Milenković I, et al. Geometric morphometry of Phytophthora plurivora sporangia. Ann For Res. 2015;58(2): 275–294.
37. Taralova EH, Schlecht J, Barnard K. Modelling and visualizing morphology in the fungus Alternaria. Fungal Biology. 2011;115(11):1163–1173.
38. Bolton R, Boddy L. Characterization of spatial aspects of foraging mycelia cord using fractal geometry. Mycological research. 1993;97(6):762–768.
39. Fodor E, Teuşdea A, Hâruţa O. Branching patterns in fungal hyphae during the colonization of Quercus cerris and Quercus petraea litter. Symposium “Trends in European Agriculture Developement”. Timişoara Agroprint. 2008;40(1):411–419.
40. Golinski MR, Boecklen WJ, Dawe AL. Two-dimensional fractal growth properties of the filamentous fungus Cryphonectria parasitica: the effect of hypovirus infection. J Basic Microbiol. 2008;48(5):426–429.
41. Matsuura S. Colony of the fungus Aspergillus oryzae and self-affine fractal geometry of growth fronts. Fractals. 1993;1:11.
42. Mihail JD, Obert M, Taylor S, et al. The fractal dimension of young colonies of Microphomina phaseolina produced from microsclerotia. Mycologia. 1994;86(3):350–356.
43. Obert M, Pfeifer P, Sernetz M. Microbial growth patterns described by fractal geometry. J Bacteriol. 1990;172(3):1180–1185.
44. Papagiani M. Quantification of the fractal nature of mycelia aggregation in Aspergillus niger submerged cultures. Microb Cell Fact. 2006;5:5.
45. Ritz K, Crawford JW. Quantification of the fractal nature of colonies of Trichoderma viride. Mycological Research. 1990;94(8):1138–1141.
46. Stanton D, Horn M. Epiphytes as “filter drinkers”: life-form changes across a fog gradient. The Bryologist. 2013;116(1):34–42.
47. Heaton L, Obara B, Grau V, et al. Analysis of fungal networks. Fungal ecology. 2012;26:12–29.
48. Bebber DP, Tlalka M, Hynes J, et al. Imaging complex nutrient dynamics in mycelial networks. In: Gadd G, Watkinson SC, Dyer P, editors. Fungi in the Environment. Cambridge University Press, 2007b: 3e21.
49. Infantino A, Zaccardelli M, Costa C, et al. A new disease of grasspea (Lathyrus sativus) caused by Ascochyta lentis var. lathyri. Journal of Plant Pathology. 2016;98(3):541–548.
50. Pringle A, Vellinga E. Peay K. The shape of fungal ecology: does spore morphology give clues to a species’ niche? Fungal Ecology. 2015;17:213–216.
51. Prenowitz W, Jordan M. Basic Concepts in Geometry. Ardsley House Publishers, Inc. 4720 Boston Way, Lanham; 1989.
52. Evans ME, Schröder-Turk GE. In a material world: Hyperbolic geometry in biological materials. Asia Pacific Mathematics Newsletter. 2015;5(2):21–30.
53. Shi J, Thompson PM, Wang Y. Hyperbolic ricci flow and its application in studying lateral ventricle morphometry. In: Yap PT, Liu T, Shen D, editors. Multimodal brain image analysis. MBIA 2012. Lecture Notes in Computer Science, vol 7509. Springer, Berlin, Heidelberg; 2012.
54. Wen C, Wang D, Shi L. Landmark constrained registration of high-genus surface applied to vestibular system morphometry. Comput, Med. Imaging Graph. 2015;44:1-12.
55. Gaston KJ, O'Neill MA. Automated species identification. Why not? Phil Trans R Soc Lond B. 2004;359:655-667.
56. Gauld ID, O’Neill MA, Gaston KJ. Driving Miss Daisy: the performance of an automated insect identification system. In: Austin AD, Dowton M, editors. Hymenoptera: evolution, biodiversity and biological control. Collingwood, VIC: CSIRO; 2000:303–312.
57. Arbuckle T, Schröder S, Steinhage V, et al. Biodiversity informatics in action: identification and monitoring of bee species using ABIS. Int Symp Informatics for Environmental Protection. 2001;1:425–430.
58. Jonker R, Groben R, Tarran G, et al. Automated identification and characterization of microbial populations using flow cytometry: the AIMS project. Scientia Mar. 2000;64:225–234.