Dynamic Optimal Control Model for Periodic Multiple Chemotherapy (PMC) Treatment of Dual HIV-Pathogen Infections

doi:10.15406/japlr.2017.06.00176

In pursuant of some vital models for HIV dynamics and treatment progression, we identified and formulated as penultimate model, a set of 7–Dimension classical mathematical model, which accounted for the dynamical interplay of dual HIV – parasitoid pathogen infections on dual immune systems, studied using multiple chemotherapy cocktail in the presence of enhanced immune effectors response. The model was considered as a continuous multiple chemotherapy treatment (MCT) and as periodic multiple chemotherapy treatment (PMC), transformed to an optimal control problem. The positivity of the model state variables and stability properties was conducted. Deploying classical optimal control theory, the model used Pontryagin’s maximum principle to investigate the existence of optimal control strategy, established the optimality control system and justified the uniqueness of the system solutions. Numerical methods were explored to numerically solve the existing model via Runge–Kutter – 4 in a Mathcad surface. The result of the numerical analysis did not only identified PMC treatment as possible technique for the reduction of drug side–effects and suppression of dual HIV –pathogen infection by enhanced immune effectors response but largely established continuous MCT, which indicated complete elimination of dual HIV – pathogen viruses and provided window for quantification of minimized systemic cost as a more formidable approach in tackling the menace of the of the deadly dual infectivity. Thus, a broader verification and application of the model to related infectious disease is therefore suggested.

Keywords: multiple–chemotherapy–treatment, periodic–multiple–chemotherapy, dual–hiv–pathogen–infection, immune–effectors–response, optimal–weight–factor, optimal–control–measures, penalty–condition

MCT: multiple chemotherapy treatment; PMC: periodic multiple chemotherapy treatment; HIV: human immune deficiency virus; AIDS: acquired immune deficiency syndrome; STI: structured treatment interruptions; ODEs: ordinary differential equations;

In spite of lack of complete eradication of the world most acclaimed viral disease – the human immune deficiency virus (HIV), which often snowball into the deadly – acquired immune deficiency syndrome (AIDS), a lot has been tinkered by research scientists in the area of suppression and elimination of these infectious diseases and its affiliated pathogenic infections. Furthermore, following the multiplicity of HIV infections, with closest limitations, which inevitably assume the motivating factors of this present study, is the methodological application of multiple chemotherapies. A factor that comes along with the impairment of drugs resistance on continuous prolong treatment. Not left out are the consequences of optimal cost benefit from these chemotherapies as well as the determinative factors of CD8 immune effector cells and other immune responders considered as key players in the established viral load and pathogenic infection set–points.^1,2 From the study on dynamic multidrug therapies for HIV with optimal and structured treatment interruptions (STI) control approaches, the model.¹ described the interaction of the immune system with HIV and permitted drug “cocktail” therapies in the presence of structured treatment interruptions. The result showed how STI therapies can lead to long control of HIV by the immune response system after discontinuation of therapy.

Moreso, considering prevalence and strength of CD8 effector cells and other immune response, which affects disease progression rate, the models.^3,4 formulated treatment strategies that aimed at boosting adaptive cellular immune responses. Other models that accounted for structured treatment interruption strategies for single viral load infection treatment as well as the use of STI strategies includes.^5–10 Interesting, all the above models focuses on STI for single viral load infections, while the models.^2,11 had considered multiple treatment of dual HIV infectivity. Model.² studied quantitative approach to parametric identifiability of dual HIV – parasitoid infection; while the model.¹¹ investigated the analysis of parametric HIV infectivity and optimal control for the treatment of dual HIV–parasitoid pathogen infection. The results of both investigations were of immense contribution to the evaluation and suppression of viral load and pathogenic infections.

Therefore, in deploying ordinary differential equations (ODEs), the present study is formulated as a 7–Dimensional dual HIV–pathogen dynamic differential model. We present the model as an optimal control problem and the method of analysis explores classical numerical method – the Pontryagin maximum principle. The method leads to the establishment of existence and uniqueness of optimality control solution. The methodological application of the study involves clinical chemotherapy cocktail from the class of antiretroviral therapies known as reverse transcriptase inhibitors (RTIs) and protease inhibitors (PIs), collectively called highly active antiretroviral therapy (HAART). Inclusively, the combination of RTI and PIs drugs increases CD4⁺ T cell count, which are the target cells of viral load and pathogeneses.¹² Thus, the present model, which utilizes drug cocktail from RTI and PIs, is formulated as a dynamic intermittent (periodic) treatment and methodological application of periodic multiple chemotherapies (PMC) for the prevention and suppression of dual viral load and pathogenic infections on host vector – human immune system. Furthermore, the model is task with the maximization of healthy CD4⁺ T cells and minimization of optimal cost, a procedure that adopts the application of optimal control technique (approach). For more details on the above, we refer readers to the models.^13–17 Therefore, the present paper as against those mentioned above, is aimed at resolving the pertinent issues in the range of methodological application of periodic multiple chemotherapies, complete zero application of optimal control measures on multiple drug cocktail, periodic alternate zero application of multiple drug cocktail, maximization of healthy CD4⁺ T cell count and evaluation of the strength of immune responses; and as well, the minimization of systemic cost. Two more important factors apprehensive of this model are drug validity period, which often span within 500–750 days before the onset of drug side–effect and drug resistivity.^{7,9,13,15,17–19} and initiation of treatment time from onset of infection, the detail which can be found in.²

Thus, the structural content of this work is characterized by eight sections, with section 1, covering the introductory aspect. Devoted in section 2, is the material and method used for the formulation and schematic presentation of the model as a classical 7–Dimensional mathematical differential model. The corresponding optimal control strategy and optimality system characterized by optimal control solution forms the fulcrum of section 3. Section 4 is devoted to the formulation and derivation of optimal multiple periodic chemotherapy (MPC) theoretical approach for the control of viral load and parasitoid–pathogen. In section 5 we conducted numerical computations for the continuous optimal multiple chemotherapy without control measures on treatment factors. The model is stepped further with the numerical simulations for the continuous multiple chemotherapy treatment with control measures on treatment optimal weight factors in section 6. Constituting section 7 is an explicit discussion of the results of conducted experiment. Finally, incisive model conclusion and recommendations are given in section 8. It is anticipated that this present study will offer a brighter hope to the eradication of the deadly disease.

The material and methods of this study is subdivided into two sections (2 and 3) respectively. Embedded in section 2, are the schematic representation of system model followed by derivation of model optimal control problem. We also show here that the state variables are non–negative and as well, ascertain the stability behavior of the system. Section 3, is devoted to the formulation of optimal control strategy and the optimality system of the model, which explores classical numerical methods known as Pontryagin maximum principle.

Schematic representation and model formulation

In structuring the progression of this model, we condone the fact that there are two virions (viral load and pathogen), which attack the immune system composing of two target cells (T–lymphocytes and macrophages). The scheme adopts the introduction of two chemotherapy cocktail (RTI and PIs) and taken into cognizance, natural interplay of adaptive immune effectors response. Thus, the model is constituted by 7 – subgroups, schematically represented as in Figure 1 below:

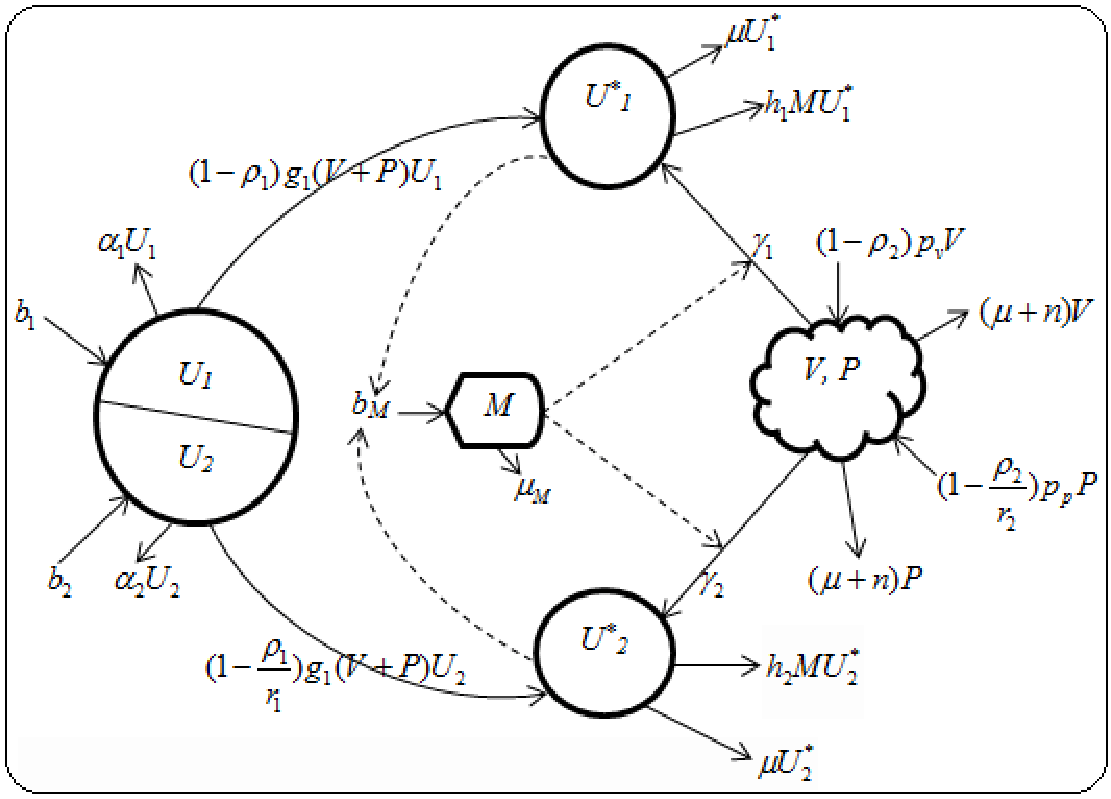
Figure 1 Schematic representation of dual HIV-pathogen infection with PMC treatment.

Obviously, from Figure 1, if these subgroups represent the population variables, with unit volume $m m^{3}$ , then we define as follows: $U_{i}$ i=1, 2 as uninfected T–lymphocytes and macrophages cells, $U_{i}^{*}$ , i=1, 2 as infected T–lymphocytes and macrophages cells, V – viral load, P – pathogen and M – immune effectors. Therefore, using classical ODEs, the simulative interactions of the above biological structure, is the formulation of a 7–Dimensional dynamic optimal control problem having its physiological derivation as follows:

$U_{1}^{'} = b_{1} - α_{1} U_{1} - (1 - ρ_{1}) g_{1} (V + P) U_{1}$ (1)

$U_{2}^{'} = b_{2} - α_{2} U_{2} - (1 - \frac{ρ_{1}}{r_{1}}) g_{2} (V + P) U_{2}$ (2)

$U_{1}^{*}^{'} = (1 - ρ_{1}) g_{1} (V + P) U_{1} - μ U_{1}^{*} - h_{1} M U_{1}^{*}$ (3)

$U_{2}^{*}^{'} = (1 - \frac{ρ_{1}}{r_{1}}) g_{2} (V + P) U_{2} - μ U_{2}^{*} - h_{2} M U_{2}^{*}$ (4)

$V^{'} = (1 - ρ_{2}) p_{p} V - (μ + n) V - [(1 - ρ_{1}) γ_{1} g_{1} U_{1} + (1 - \frac{ρ_{1}}{r_{1}}) γ_{2} g_{2} U_{2}] V$ (5)

$P^{'} = (1 - \frac{ρ_{2}}{r_{2}}) p_{p} P - (μ + n) P - [(1 - ρ_{1}) γ_{1} g_{1} U_{1} + (1 - \frac{ρ_{1}}{r_{1}}) γ_{2} g_{2} U_{2}] P$ (6)

$M^{'} = b_{M} + \frac{w_{M} (U_{1}^{*} + U_{2}^{*})}{(U_{1}^{*} + U_{2}^{*}) + H_{w}} M - \frac{q_{M} (U_{1}^{*} + U_{2}^{*})}{(U_{1}^{*} + U_{2}^{*}) + H_{q}} M - μ_{M} M$ (7)

with initial values $U_{1} (0) = U_{(1)}_{0}, U_{2} (0) = U_{(2)}_{0}, U_{1}^{*} (0) = U_{_{(1)}}^{*}_{0}, U_{2}^{*} (0) = U_{_{(2)}}^{*}_{0}, V (0) = V_{0}, P (0) = P_{0}$ and $M (0) = M_{0}$ for all $t = t_{0}$ and which satisfies the biological variables and parameter values as defined in Tables 1 & 2 below. The present model is in tune with the investigation by.²⁰ where the author accounted for only single drug–RTI on single infection – HIV; and the study.¹ accounted for chemotherapy “cocktail” (RTI and PIs) used for the study of dynamics of single infection–HIV.

Variables	Dependent Variables
Variables	Definition	Initial Values	Units
U₁	Uninfected T-lymph cells population	0.4	cells/mm³
U₂	Uninfected macrophages cells population	0.2	cells/mm³
U^*₁	Infected T-lymph cells population	0.1	-
U^*₂	Infected macrophages cells population	0.1	-
V	Infectious viral load population	0.2	mm³
P	Infectious pathogen population	0.1	mm³
M	Immune effectors response	10	mm³day^-1

Table 1 Values used for state variables of model (2.1)-(2.7)

Laconically, equations (1)–(7) present the model of the system and the epidemiological terms are carefully defined thus: in equation (1), $b_{1}$ – the source term of uninfected CD4⁺ T–lymphocytes and $α_{1} U_{1}$ – the death rate of uninfected T–lymphocytes cells. The term $(1 - ρ_{1}) g_{1} (V + P) U_{1}$ is the interplay of viruses $(V, P)$ with infectivity rate $g_{1}$ , and $ρ_{1} (t)$ – drug efficacy, which model the RTI that block new infections, in $U_{1}, U_{2}, U_{1}^{*}$ and $U_{2}^{*}$ of the population. From equation (2), $b_{2}$ – source term of uninfected macrophages cells, $α_{2} U_{2}$ – the death rate of uninfected macrophages cells. Here, the term $(1 - ρ_{1} / r_{1}) g_{2} (V + P) U_{2}$ – represents the balance of treatment of viruses with infectivity rate $g_{2}$ , on $U_{2}$ and $ρ_{1} / r_{1}$ – as treatment efficacy reduction in population $U_{2}$ . The implication is that $g_{1}, g_{2}$ and the ratio $1 / r_{1}$ constitutes the difference between the two cell populations. For these two cells, we assume that $0 \leq x_{1} \leq ρ_{1} (t) \leq y_{1} < 1$ , such that $x_{1}$ and $y_{1}$ denotes minimal and maximal drug efficacy respectively with $r_{1} \in [0, 1]$ .

In equations (3) and (4), the first terms $(1 - ρ_{1}) g_{1} (V + P) U_{1}$ and $(1 - ρ_{1} / r_{1}) g_{2} (V + P) U_{2}$ are the results of the interactions of free CD4⁺ T–lymphocytes and macrophages with free virions $(V, P)$ infectivity and the activation of proportionate (RTI) drug on infected $U_{1}^{*}$ and $U_{2}^{*}$ . The terms on infected $μ U_{1}^{*}$ and $μ U_{2}^{*}$ are the death rates of infected $U_{1}^{*}$ and $U_{2}^{*}$ . At the onset of infection, the third terms $h_{i} M U_{i}^{*}$ , i=1, 2, represents the cytotoxic T–lymphatic (CTL) also known as CD8⁺T cells, which exhibit the tendency of detecting and killing infected cells as much as possible. Therefore, in equations (3) and (4), terms $h_{i} M U_{i}^{*}$ , i=1, 2, defines death of infected cells at the rate $h_{i} M$ , which depends on the density of immune effectors M.

$J = (\begin{matrix} - α_{1} - g_{1} (V + P) & 0 & 0 & 0 & - g_{1} U_{1} & - g_{1} U_{1} & 0 \\ 0 & - α_{2} - g_{2} (V + P) & 0 & 0 & - g_{2} U_{2} & - g_{2} U_{2} & 0 \\ g_{1} (V + P) & 0 & - μ - h_{1} M & 0 & g_{1} U_{1} & g_{1} U_{1} & - h_{1} U_{1}^{*} \\ 0 & g_{2} (V + P) & 0 & - μ - h_{2} M & g_{2} U_{2} & g_{2} U_{2} & - h_{2} U_{2}^{*} \\ - γ_{1} g_{1} V & - γ_{2} g_{2} V & 0 & 0 & \begin{array}{l} p_{v} - (μ + n) - (γ_{1} g_{1} U_{1} \\ + γ_{2} g_{2} U_{2}) \end{array} & 0 & 0 \\ - γ_{1} g_{1} P & - γ_{2} g_{2} P & 0 & 0 & 0 & \begin{array}{l} p_{p} - (μ + n) - (γ_{1} g_{1} U_{1} \\ + γ_{2} g_{2} U_{2}) \end{array} & 0 \\ 0 & 0 & B_{7, 3} & B_{7, 4} & 0 & 0 & B_{7, 7} \end{matrix})$ (10)

From equation (5), the first term $(1 - ρ_{2}) p_{v} V$ defines the control function with $ρ_{2} (t)$ , representing the efficacy of protease inhibitors and having viral load multiplicative capacity $p_{v}$ . The second term $(μ + n) V$ defines reduction of infected cells due to clearance rate and the natural death rate of viral load. Thus, the productivity $p_{v}$ is reduced to $(1 - ρ_{2}) p_{v}$ , where $0 \leq x_{2} \leq ρ_{2} (t) \leq y_{2} < 1$ . The cumulative effect of viral load on both targeted cells in $U_{1}$ and $U_{2}$ is represented by the term $- [(1 - ρ_{1}) γ_{1} g_{1} U_{1} + (1 - ρ_{1} / r_{1}) γ_{2} g_{2} U_{2}] V$ , which reveal $γ_{i}$ , i=1, 2 as probability of multiple virions infections on target cells $U_{1}$ and $U_{2}$ . In a chronological manner, equation (6) can be interpreted as in equation (5) but with respect to pathogenic infection and having differential effect of $1 / r_{2}$ as treatment reduction efficacy on $U_{1}^{*}$ and $U_{2}^{*}$ .

Remarkably, the clearance rate of infected cells.¹ is conspicuously visible through the immune effector cells (CTL), designated by M, of equation (7). The dynamics of $M^{'}$ is adopted from the study of.²¹ The term $b_{M}$ – denotes the replication (or proliferation) of more effector cells from the co–existence of infected cell and immune effector cells. The second term $w_{M} (U_{1}^{*} + U_{2}^{*}) M / (U_{1}^{*} + U_{2}^{*}) + H_{w}$ – defines the maximum birth rate of immune effectors in the presence of infected cells $U_{1}^{*}$ , $U_{2}^{*}$ and $M$ ; and having saturation birth constant $H_{w}$ . The third term $q_{M} (U_{1}^{*} + U_{2}^{*}) M / (U_{1}^{*} + U_{2}^{*}) + H_{q}$ is attributed to immune effector maximum death rate, where $H_{q}$ is the effector death saturation constant. Lastly, the term $μ_{M} M$ is the immune effectors natural death rate. Thus, the aforementioned descriptions are relevant in the administration of chemotherapy cocktail and PMC scenarios. Furthermore, the inclusion of immune effectors is a direct consequence of the sensitive role in the practical sense of PMC, which we will illustrate in the course of our numerical simulations.

From model (1)–(7) we observe that the function $ρ_{i} (t)$ , $i = 1, 2$ , determines the percentage drug efficacy and the maximal use of chemotherapies. Thus, $ρ_{i} (t)$ is a measurable function having limit $t \in [t_{0}, t_{f}]$ on the domain $0 \leq ρ_{i} (t) \leq 1$ . This time interval accounts for the design of periodic treatment and as well, satisfies the objectives of this study as clearly mentioned in the introductory section. Furthermore, to ensure that our objective functional satisfies the control system, we take $t \in [t_{0}, t_{f}]$ such that $t \leq 30$ months of drugs allowable validity period.^2,13,18

Therefore, the validity of the system equations (1)–(7) comes to bear, if we can genuinely generate compactible numerical values for the variables and parameters of the model. Attaining this, we adopt to the closest parameters values from those existing and valid studies as contain in our literature.^1,14,17 Thus, the simulative parameter values that satisfy the biological variables and parameters of our model are explicitly defined as in Tables 1 & 2 below:

Parameter	Parameter and Constants
Parameter	Definition	Initial Values	Units
b₁	Source of new T-lymph cells rate	100	cell/mm³.day
b₂	Source of new macrophages cells rate	20	cell/mm³.day
α₁	Death rate of uninfected T-lymph cells	0.02	day^-1
α₂	Death rate of uninfected macrophages cells	0.02	day^-1
g₁	Infected rate of T-lymph cells	0.004	mm³vir.^-1d^-1
g₂	Infected rate of macrophages cells	0.001	mm³vir.^-1d^-1
ρ₁	Treatment rate of RTI on U₁,U^₁,U₂ and U^₂	$\in [0.5)$	-
ρ₂	Treatment rate of PIs on V and P	$\in [0.3)$	-
r_i-1,2	Treatment efficacy reduction in U₂ and U^*₂	0.14	-
P_v	Viral load multiplicity capacity	0.20	virions/cells
P_p	Macrophages multiplicity rate	0.04	virions/cells
μ	Infected virions death rate	0.07	day^-1
n	Virions natural death rate	0.02	day^-1
γ₁	Probability of multiple virions infection of T-lymph cells	1	virions/cells
γ₂	Probability of multiple virions infection of macrophages cells	1	virions/cells
h₁	Rate of death of infected T-lymph cells induced by immune effectors	0.004	mm³cell^-1.d^-1
h₂	Rate of death of infected macrophages cells induced by immune effectors	0.004	mm³cell^-1.d^-1
b_M	Immune effectors replication rate	0.06	cell/mm³.day
w_M	Immune effectors maximum birth rate	0.03	day^-1
H_w	Immune effectors saturation birth rate	10	cells/mm
q_M	Immune effectors maximum death rate	0.02	day^-1
H_q	Immune effectors saturation death rate	30	cells/mm
μ_M	Immune effectors natural death rate	0.01	day^-1
C₁	Half saturation constants for U^₁,U^₂	100	mm³
C₂	Half saturation constants for V,P	10	mm³
C₃	Half saturation constants for M	100	mm³

Table 2 Summary of model parameter values for (2.1)-(2.7)
Note: The table above is a reflection of models. ^1,14,15,17 but clinically modified to accommodate the present novel model and compactible with RK4 software application utilized in this investigation.

Next, to satisfactorily establish the optimality and methodological application of our chemotherapy cocktail, it become necessary to first show that model state variables are non–negative and as well, discuss the disease stability analysis.

Positivity and compatibility of model variables

It is obvious that since maximal cost of chemotherapy cocktail is given by

${(ρ_{1} (t) + ρ_{2} (t))}^{2}$ , then possible drug severities is accounted for by the following proposition.

Proposition 2.1: If drug severities (or drug hazardous side–effects) emerges in the course of treatment, then the introduction of optimal weight factors ${K_{i} \geq 0, L_{i} \geq 0, δ \geq 0}_{i = 1, 2}$ is justified. Also, if ${x_{i}, y_{i}}_{i = 1, 2}$ represents minimal and maximal drugs efficacies, then the inequality $0 \leq x_{i} \leq {K_{i} (t), L_{i} (t), δ (t)} \leq y_{i} < 1$ , i =1, 2 holds. Therefore, positivity for which model variables are compactible is studied using the following theorem.

Theorem 2.1: If equations (1)–(7) represents the model equations, such that for $ϕ = {\begin{cases} U_{1}, U_{2}, U_{1}^{*}, U_{2}^{*}, V, P, M \in ℝ_{+}^{7} : U_{1} (0) > 0, U_{2} (0) > 0, U_{1}^{*} (0) > 0, U_{2}^{*} (0) > 0, \\ V (0) > 0, P (0) > 0, M (0) > 0 \end{cases}}$ , then the solution of the system ${U_{1} (t), U_{2} (t), U_{1}^{*} (t), U_{2}^{*} (t), V (t), P (t), M (t)}$ are non–negative and compactible for all $t \geq 0$ .^22–24

Proof: We show that the state variables are life varying integers. Thus, invoking equations (1)–(7) step–wisely, we differentiating each of each them to justify their non–negativity.

From equation (1), we have $U_{1}^{'} = b_{1} - α_{1} U_{1} - (1 - ρ_{1}) g_{1} (V + P) U_{1}$ . Differentiating with respect to $U_{1}$ , we obtain $\frac{d U_{1}}{d t} \geq - α_{1} U_{1}$ $\Rightarrow$ $\frac{d U_{1}}{d t} + α_{1} U_{1} \geq 0$ . Since $t \geq 0$ , then $U_{1} = + \infty$ and is positive. The integrating factor IF is given by $I F = e^{\int α_{1} d t} = e^{α_{1} t}$ . Multiplying the equation by the integrating factor, we have $e^{α_{1} t} {U_{1}^{'} + (α_{1}) U_{1}} \geq 0$ . Rewriting the left hand side of the equation, we obtain $\frac{d}{d t} (e^{α_{1} t} U_{1}) \geq 0$ .

Integrating both sides, leads to $\frac{d}{d t} (e^{α_{1} t} U_{1}) \geq 0$ . Dividing by the integrating factor, we have $U_{1} (t) = C e^{α_{1} t}$ . Applying the initial condition i.e. $t = 0$ , $U_{1} (t) = U_{1} (0) . U_{1} (0) \geq C$ , then $U_{1} (t) \geq U_{1} (0) e^{α_{1} t} \geq 0$ , $t \geq 0$ . Therefore, $U_{1} (t) \geq 0$ is non–negative and compactible. Next, taking equation (2), we set

$\frac{d U_{2}}{d t} = b_{2} - α_{2} U_{2} - (1 - \frac{ρ_{1}}{r_{1}}) g_{2} (V + P) U_{2}$

Differentiating, we have, $\frac{d U_{2}}{d t} \geq - α_{2} U_{2}$ and taking the integral gives $\int \frac{d U_{2}}{U_{2}} \geq - \int α_{2} d t$ . Then applying the integrating factor $I F = e^{- α_{2} t}$ , we have $U_{2} (t) \geq U_{2} (0) e^{- α_{2} t} \geq 0$ , $t \geq 0$ . Applying initial condition at $t = 0$ , $U_{2} (t) \geq U_{2} (0)$ . Therefore, for $t \to \infty$ , $U_{2} (t) \geq 0$ . Similarly, from equation (3), we have,

$\frac{d U_{1}^{*}}{d t} = (1 - ρ_{1}) g_{1} (V + P) U_{1} - μ U_{1}^{*} - h_{1} M U_{1}^{*}$ .

Differentiating, we see that $\frac{d U_{1}^{*}}{d t} \geq - μ U_{1}^{*}$ $\Rightarrow$ $\frac{d U_{1}^{*}}{U_{1}^{*}} \geq - μ d t$ and taking the integral gives $\int \frac{d U_{1}^{*}}{U_{1}^{*}} \geq - \int μ d t$ . Applying the integrating factor $I F = e^{- μ t}$ , we have $U_{1}^{*} (t) \geq U_{1}^{*} (0) e^{- μ t} \geq 0$ , $t \geq 0$ . Hence, $t \to \infty$ , $U_{1}^{*} (t) \geq 0$ .

From equation (4), we have, $U_{2}^{*}^{'} = (1 - \frac{ρ_{1}}{r_{1}}) g_{2} (V + P) U_{2} - μ U_{2}^{*} - h_{2} M U_{2}^{*}$ . Differentiating with respect to $U_{2}^{*}$ , we obtain, $\frac{d U_{2}^{*}}{d t} \geq - μ U_{2}^{*}$ $\Rightarrow$ $\frac{d U_{2}^{*}}{U_{2}^{*}} \geq - μ d t$ and taking the integral gives $\int \frac{d U_{2}^{*}}{U_{2}^{*}} \geq - \int μ d t$ . Applying the integrating factor $I F = e^{- μ t}$ , we have $U_{2}^{*} (t) \geq U_{2}^{*} (0) e^{- μ t} \geq 0$ , $t \geq 0$ . When $t \to \infty$ , . Furthermore, taking equation (5), we set $V^{'} = (1 - ρ_{2}) p_{p} V - (μ + n) V - [(1 - ρ_{1}) γ_{1} g_{1} U_{1} + (1 - \frac{ρ_{1}}{r_{1}}) γ_{2} g_{2} U_{2}] V .$

Differentiating with respect to $V$ , we obtain, $\frac{d V}{d t} \geq [(1 - ρ_{2}) p_{v} - (μ + n)] V$ $\Rightarrow$ $\frac{d V}{V} \geq [(1 - ρ_{2}) p_{v} - (μ + n)] d t$ .

Taking the integral gives the expression $\int \frac{d V}{V} \geq \int [(1 - ρ_{2}) p_{v} - (μ + n)] d t$ . Now, applying the integrating factor $I F = e^{[(1 - ρ_{2}) p_{v} - (μ + n)] t}$ , we have $V (t) \geq V (0) e^{[(1 - ρ_{2}) p_{v} - (μ + n)] t} \geq 0$ , $t \geq 0$ . Therefore, when $t \to \infty$ , $V (t) \geq 0$ .

Taking equation (6), we have $P^{'} = (1 - \frac{ρ_{2}}{r_{2}}) p_{p} P - (μ + n) P - [(1 - ρ_{1}) γ_{1} g_{1} U_{1} + (1 - \frac{ρ_{1}}{r_{1}}) γ_{2} g_{2} U_{2}] P$ . Differentiating with respect to P, we obtain, $\frac{d P}{d t} \geq [(1 - \frac{ρ_{2}}{r_{2}}) p_{p} - (μ + n)] P$ $\Rightarrow$ $\frac{d P}{P} \geq [(1 - \frac{ρ_{2}}{r_{2}}) p_{p} - (μ + n)] d t .$ Taking the integral gives the expression $\int \frac{d P}{P} \geq \int [(1 - \frac{ρ_{2}}{r_{2}}) p_{p} - (μ + n)] d t$ . Now, applying the integrating factor $I F = e^{[(1 - \frac{ρ_{2}}{r_{2}}) p_{p} - (μ + n)] t}$ , we have $P (t) \geq P (0) e^{[(1 - \frac{ρ_{2}}{r_{2}}) p_{p} - (μ + n)] t} \geq 0$ , $t \geq 0$ . Therefore, when $t \to \infty$ , $P (t) \geq 0$ .

Finally, from equation (7), we have, $M^{'} = b_{M} + \frac{w_{M} (U_{1}^{*} + U_{2}^{*})}{(U_{1}^{*} + U_{2}^{*}) + H_{w}} M - \frac{q_{M} (U_{1}^{*} + U_{2}^{*})}{(U_{1}^{*} + U_{2}^{*}) + H_{q}} M - μ_{M} M$ .

Differentiating with respect to M, we obtain, $\frac{d M}{d t} \geq - μ_{M} M$ $\Rightarrow$ $\frac{d M}{M} \geq - μ_{M} d t .$ Taking the integral gives the expression $\int \frac{d M}{M} \geq \int - μ_{M} d t$ . Now, applying the integrating factor $I F = e^{- μ_{M} t}$ , we have $M (t) \geq M (0) e^{- μ_{M} t} \geq 0$ , $t \geq 0$ . Therefore, when $t \to \infty$ , . Hence, all the model variables are non–negative and this completes the proof. We complete this section by highlighting the properties for which the PMC model is locally asymptotically stable.

Model stability analysis

Though the system stability analysis seems somewhat complex due to the nature of nonlinear systems involved, we’ll discuss the existing stability properties of the model in a simpler manner. Suppose, $ν = (U_{1}, U_{2}, U_{1}^{*}, U_{2}^{*}, V, P, M)$ defines the vectorial capacity of the model, then the system (1)–(7) satisfies the equation

$\frac{d ν (t)}{d t} = f (t, ν; z)$ (8)

Where $f (t, ν; z)$ is the right–side of the ODE system and , the vector parameters as in Table 2. Then, we implore the Runge–Kutter of order 4, to solve the equation $f (t, ν; z) = 0$ for the steady states ${\bar{ν}}_{k}$ . Next, we calculate the Jacobian matrix of the partial derivatives of the right side of the differential equations with respect to the state variables, i.e. $\frac{\partial f (t, ν; z)}{\partial ν} = [\frac{\partial f_{i} (t, ν; z)}{\partial ν_{j}}]$ (9).

From equation (1)–(7), if we let $ρ_{1} = ρ_{2} = 0$ for the simple reason that we are poised to establish the system stability behavior when off treatment is applied, then the Jacobian matrix is derive as:

$J = (\begin{matrix} - α_{1} - g_{1} (V + P) & 0 & 0 & 0 & - g_{1} U_{1} & - g_{1} U_{1} & 0 \\ 0 & - α_{2} - g_{2} (V + P) & 0 & 0 & - g_{2} U_{2} & - g_{2} U_{2} & 0 \\ g_{1} (V + P) & 0 & - μ - h_{1} M & 0 & g_{1} U_{1} & g_{1} U_{1} & - h_{1} U_{1}^{*} \\ 0 & g_{2} (V + P) & 0 & - μ - h_{2} M & g_{2} U_{2} & g_{2} U_{2} & - h_{2} U_{2}^{*} \\ - γ_{1} g_{1} V & - γ_{2} g_{2} V & 0 & 0 & \begin{array}{l} p_{v} - (μ + n) - (γ_{1} g_{1} U_{1} \\ + γ_{2} g_{2} U_{2}) \end{array} & 0 & 0 \\ - γ_{1} g_{1} P & - γ_{2} g_{2} P & 0 & 0 & 0 & \begin{array}{l} p_{p} - (μ + n) - (γ_{1} g_{1} U_{1} \\ + γ_{2} g_{2} U_{2}) \end{array} & 0 \\ 0 & 0 & B_{7, 3} & B_{7, 4} & 0 & 0 & B_{7, 7} \end{matrix})$ (10)

Where

$B_{7, 3} = B_{7, 4} = \frac{w_{M} H_{w} M}{{(U_{1}^{*} + U_{2}^{*} + H_{w})}^{2}} - \frac{q_{M} H_{q} M}{{(U_{1}^{*} + U_{2}^{*} + H_{q})}^{2}}$

and

$B_{7, 7} = (\frac{w_{M}}{U_{1}^{*} + U_{2}^{*} + H_{w}} - \frac{q_{M}}{U_{1}^{*} + U_{2}^{*} + H_{q}}) U_{1}^{*} + U_{2}^{*} - μ_{M}$ .

So equation (10) exhibits non–singularity behavior since the diagonal of the Jacobian matrix is non–zero.

Then if we substitute the resulting computation of ${\bar{ν}}_{k}$ steady state for v, in equation (10), we obtain the ODE system dynamics that is linearized about the equilibrium ${\bar{ν}}_{k}$ . So we see from here that linearized ODE theory ascertain the fact that if the eigenvalues of the matrix have all negative real parts, then the equilibrium ${\bar{ν}}_{k}$ is locally asymptotically stable. Therefore, given specific parameter values as in Tables 1 & 2, the model (1)–(7) exhibits three physical steady states and several non–physical steady states (omitted here for brevity). Thus, it is of interest to note that detail analysis of these stability behaviors is left to readers with related analysis as in model.^1,8,25 This thought is in line with the focus of the present study – optimization control of PMC treatment and the maximization of CD4⁺ T cells and macrophages.

Unlike model.¹ which considered single infection (HIV) in two immune systems with dual chemotherapy cocktail under STI program and which the method of analysis explored stability and linearization technique, the present model consider dual infectious variables under PMC program and focuses on utilizing classical numerical method known as Pontryagin’s maximum principle. This method allows the verification of existence of model as a function and the uniqueness of the system solution. To accomplish this task, we establish the model optimality control strategy from the derived optimal control problem.

Optimal control strategy and optimality system

Having shown that the model state variables are non–negative with known stability behavioral pattern, we then establish in this section, the optimal control strategy for continuous chemotherapy cocktail and the consequences following the introduction of optimal weight factors. This will lead to the derivation of existence of the model, establish the model optimality control system and lastly, prove the uniqueness of the solution of the system.

Optimal control strategy for continuous chemotherapy cocktail

We recall that optimal control strategy is the derivation of mathematical model (as in this case of model (1)–(7)) with which we define the objective functional as a function of maximization of the control variables. Indeed the objective functional of any optimal control problem is an integral equation, which model the trade–off between virions and pathogen concentration, organ health and use of therapeutics.^26,27 Therefore, for a HIV–pathogen dynamics having optimal control problem as in equations (1)–(7), the objective functional that maximizes the control system is derive as:

$R (ρ_{1}, ρ_{2}) = \int_{t_{0}}^{t_{f}} [K_{1} V (t) + K_{2} P (t) + L_{1} ρ_{1}^{2} + L_{2} ρ_{2}^{2} - δ M (t)] d t$ (12)

where $ρ_{1} (t), ρ_{2} (t)$ are the control variables for RTIs and PIs respectively. The quantities $K_{i = 1, 2}, L_{i = 1, 2}$ and δ are the optimal weight factors on the virions, control treatment inputs and immune effectors respectively. These control constants maximizes the system benefits quantified along the level of CD4⁺ T cells concentration as represented by the first and second terms of equation (12). The third and fourth terms of the equations accounts for the minimization of systemic cost of drugs treatment cocktail. So that, if $0 \leq ρ_{i = 1, 2} \leq 1$ represents maxima drug usage, then periodic zero alternate application of multiple drug cocktail is visible. Therefore, the maximal cost of drug usage is given by ${(ρ_{1} (t), ρ_{2} (t))}^{2}$ .^28,29

The introduction of optimal weight factors ${K_{i} \geq 0, L_{i} \geq 0, δ \geq 0}_{i = 1, 2}$ is a consequence of the fact that cost benefits are nonlinear. Thus, these serve as simple nonlinear controls on the system variables. And we can satisfactorily say that the objective functional (12) completely meets the aims of the present investigation, which is primed by maximization of immune systems and immune effector concentration in the presence of minimal application of systemic cost as well as maximal suppression of both viral load and pathogenic infections. Therefore, we compatibly opt for an optimal control pair $(ρ_{1}^{*}, ρ_{2}^{*})$ that is ascribes by the expression ${}_{0 \leq ρ_{i} \leq 1}^{\max}R (ρ_{i}^{*}) = \min {R (ρ_{1}, ρ_{2}) / (ρ_{1}, ρ_{2}) \in Q}_{i = 1, 2}$ subject to the system of ODEs (1)–(7) and such that $Q = {R (ρ_{1}, ρ_{2}) / ρ_{i}, Q = ρ_{i} / ρ_{i}$ is measurable with $x_{i} \leq ρ_{i} \leq y_{i}$ for all $t \in [t_{0}, t_{f}]$ , for $i = 1, 2}$ a measurable control set. This is an innovative optimal control theory, which is in line with several varying control theories formulated; see for example.^7,9,13,17,19 Next, we verify the existence of the model optimality control for a PMC treatment.

Existence of optimality control strategy

The existence of an optimality control for PMC treatment of a dual HIV–pathogen infections can be proved from the point of.¹⁰ where we possibly show that the right sides of equations (1)–(7) are bounded by a linear function of the state and control variables. Also, we show that the integrand of the objective functional (12) is concave on Q and bounded below, which again affirm the compatibility required of the model. Therefore, there exists on the basis of system boundedness of solution, super–solutions of the system ${\bar{U}}_{1}, {\bar{U}}_{2}, {\bar{U}}_{1}^{*}, {\bar{U}}_{2}^{*}, \bar{V}, \bar{P},$ and , satisfying the equation:

${\begin{cases} \frac{d {\bar{U}}_{1}}{d t} = b_{1} - [ρ_{1} (t)] {\bar{U}}_{1} \\ \frac{d {\bar{U}}_{2}}{d t} = b_{2} - [ρ_{1} (t)] {\bar{U}}_{2} \\ \frac{d {\bar{U}}_{1}^{*}}{d t} = \frac{h_{1} {\bar{U}}_{1}^{*}}{C_{1} + {\bar{U}}_{1}^{*}} \\ \frac{d {\bar{U}}_{2}^{*}}{d t} = \frac{h_{2} {\bar{U}}_{2}^{*}}{C_{1} + {\bar{U}}_{2}^{*}} \\ \frac{d \bar{V}}{d t} = \frac{ρ_{2} (t) \bar{V}}{C_{2} + \bar{V}} \\ \frac{d \bar{P}}{d t} = \frac{ρ_{2} (t) \bar{P}}{C_{2} + \bar{P}} \\ \frac{d \bar{M}}{d t} = \frac{b_{M} - (ρ_{1} (t) + ρ_{2} (t)) \bar{M}}{C_{3} + \bar{M}} \end{cases}$ ,(13)

Where $C_{i = 1, 2, 3}$ are half saturation constants on $U_{1}^{*}, U_{2}^{*}; V$ and P with equation (13) been compactly bounded on a finite time interval. Thus, determining the existence of the optimal control to the model, we invoke theorem 4.1, p. 68–69.¹⁰

Theorem 3.1: Given an optimal control system with model equations (1)–(7) and having proposition 2.1, there exists a PMC optimal control ${\vec{ρ}}^{*} = (ρ_{1}^{*}, ρ_{2}^{*}) \in Q$ such that

$\begin{matrix} \max \\ (ρ_{1}, ρ_{2}) \in Q \end{matrix} R (ρ_{1}, ρ_{2}) = R (ρ_{1}^{*}, ρ_{2}^{*})$

Proof: Taking proceeding from Thm. 4.1.¹⁰ we state and show that the following conditions are justified:

Then control set ${ρ_{i}}_{i = 1, 2}$ is Lebesgue–integrable function on interval $[t_{0}, t_{f}]$ and the corresponding state variable is nonempty.
The measurable control set Q, is convex and closed.
The right side (RHS) of the state system is continuous and bounded above by sum of the bounded control and state variables and can by written as a linear function of $ρ_{i}$ , i=1,2 , with coefficients define by proposition 2.1 and on the state variables.
The integrand of the objective functional is concave on the measurable set Q.
There exist consistence $b_{1}, b_{2} > 0$ and $β > 1$ , such that the integrand $L (U_{1}, U_{2}, ρ_{1}, ρ_{2})$ of the objective functional satisfies

$L (U_{1}, U_{2}, ρ_{1}, ρ_{2}) \leq b_{2} - b_{1} {({| ρ_{1} |}^{2} + {| ρ_{2} |}^{2})}^{β / 2}$ .

Then, we at once resort to the result of (.³⁰ Thm. 9.2.1, p.182) for the existence of the state system (1)–(7) with bounded coefficients, which satisfies condition (i). It is obvious that solution here is bounded. It follows by definition that our control set is closed and convex, thus satisfying condition (ii). Since, our state system is bilinear in $ρ_{1}, ρ_{2}$ , the RHS of (1)–(7) satisfies condition (iii) in the sense of boundedness of solutions. Furthermore, the integrand of the objective functional $(K_{1} V (t) + K_{2} P (t) + L_{1} ρ_{1}^{2} + L_{2} ρ_{2}^{2} - δ M (t))$ is concave on the measurable control set Q. Finally, the completeness of the existence of solution of the optimal control lies in the established fact that $[K_{1} V (t) + K_{2} P (t) + L_{1} ρ_{1}^{2} + L_{2} ρ_{2}^{2} - δ M (t)] \leq b_{2} - b_{1} ({| ρ_{1} |}^{2} + {| ρ_{2} |}^{2})$ where $b_{2}$ depends on the upper bound on V and P; and $b_{1} > 0$ since ${L_{i}, K_{i}, δ}_{i = 1, 2} > 0$ . This completes the proof.

Optimality control system

Here, relying on the fact that we were able to prove the existence of the model equations, then we can establish the model optimality system. This is achieved by first defining the necessary conditions for an optimal control for periodic multiple treatments under dual infectious variables. Then, for equation (12), the penalty term on the constraints of the objective functional is the Hamiltonian arguments define by the Lagrangian: $L (U_{1}, U_{2}, U_{1}^{*}, U_{2}^{*}, V, P, M, τ_{1}, τ_{2}, τ_{3}, τ_{4}, τ_{5}, τ_{6}, τ_{7})$ =

$\begin{array}{l} K_{1} V + K_{2} P + L_{1} ρ_{1}^{2} + L_{2} ρ_{2}^{2} + δ M \\ + τ_{1} [b_{1} - α_{1} U_{1} - (1 - ρ_{1}) g_{1} (V + P) U_{1}] \\ + τ_{2} [b_{1} - α_{2} U_{2} - (1 - \frac{ρ_{1}}{r_{1}}) g_{2} (V + P) U_{2}] \\ + τ_{3} [(1 - ρ_{1}) g_{1} (V + P) U_{1} - μ U_{1}^{*} - h_{1} M U_{1}^{*}] \\ + τ_{4} [(1 - \frac{ρ_{1}}{r_{1}}) g_{2} (V + P) U_{2} - μ U_{2}^{*} - h_{2} M U_{2}^{*}] \\ + τ_{5} {(1 - ρ_{1}) p_{v} V - (μ + n) V - [(1 - ρ_{1}) γ_{1} g_{1} U_{1} + (1 - \frac{ρ_{1}}{r_{1}}) γ_{2} g_{2} U_{2}] V} \\ + τ_{6} {(1 - \frac{ρ_{2}}{r_{2}}) p_{P} P - (μ + n) P - [(1 - ρ_{1}) γ_{1} g_{1} U_{1} + (1 - \frac{ρ_{1}}{r_{1}}) γ_{2} g_{2} U_{2}] P} \\ + τ_{7} [b_{M} + \frac{w_{M} (U_{1}^{*} + U_{2}^{*})}{(U_{1}^{*} + U_{2}^{*}) + H_{w}} M - \frac{q_{M} (U_{1}^{*} + U_{2}^{*})}{(U_{1}^{*} + U_{2}^{*}) + H_{q}} M - μ_{M} M] \\ - q_{11} (ρ_{1} - x_{1}) - q_{12} (y_{1} - ρ_{1}) - q_{21} (ρ_{2} - x_{2}) - q_{22} (y_{2} - ρ_{2}), \end{array}$

Where $q_{i j} (t) \geq 0$ are the penalty multipliers satisfying $q_{11} (t) (ρ_{1} (t) - x_{1}) = q_{12} (t) (y_{1} - ρ_{1} (t)) = 0$ at the optimal $ρ_{1} = ρ_{1}^{*}$ and $q_{21} (t) (ρ_{2} (t) - x_{2}) = q_{22} (t) (y_{2} - ρ_{2} (t)) = 0$ at the optimal $ρ_{2} = ρ_{2}^{*}$ . The optimal control $(ρ_{1}^{*}, ρ_{2}^{*})$ to be determined leads to the following theorem.

Theorem 3.2: Let $ρ_{1}^{*}, ρ_{2}^{*}$ be the given optimal control to be determine, such that, if the system $U_{1}^{*}, U_{2}^{*}, U_{1}^{*}^{*}, U_{2}^{*}^{*}, V^{*}, P^{*}$ and $M^{*}$ are the solutions for the corresponding state variables (1)–( 7), then there exists adjoint variables $τ_{i}$ , i=1, 2... 7 satisfying

$τ_{1}^{'} = - 1 {\begin{cases} τ_{1} [- α_{1} - (1 - ρ_{1}^{*}) g_{1} (V^{*} + P^{*})] + τ_{3} [(1 - ρ_{1}^{*}) g_{1} (V^{*} + P^{*})] \\ + τ_{5} [(1 - ρ_{1}^{*}) γ_{1} g_{1} V^{*}] + τ_{6} [(1 - ρ_{1}^{*}) γ_{1} g_{1} P^{*}] \end{cases}}$

$τ_{2}^{'} = - 1 {\begin{cases} τ_{2} [- α_{2} - (1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{2} (V^{*} + P^{*})] + τ_{4} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{2} (V^{*} + P^{*})] \\ + τ_{5} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) γ_{2} g_{2} V^{*}] + τ_{6} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) γ_{2} g_{2} P^{*}] \end{cases}}$

$τ_{3}^{'} = - 1 {τ_{3} (- μ - h_{1} M^{*}) + τ_{7} (\frac{w_{M} M H_{w}}{{(U_{1}^{*} + U_{2}^{*} + H_{w})}^{2}} - \frac{q_{M} M H_{q}}{{(U_{1}^{*} + U_{2}^{*} + H_{q})}^{2}})}$

$τ_{4}^{'} = - 1 {τ_{4} (- μ - h_{2} M^{*}) + τ_{7} (\frac{w_{M} M H_{w}}{{(U_{1}^{*} + U_{2}^{*} + H_{w})}^{2}} - \frac{q_{M} M H_{q}}{{(U_{1}^{*} + U_{2}^{*} + H_{q})}^{2}})}$

$τ_{5}^{'} = - 1 {\begin{cases} K_{1} + τ_{5} [(1 - ρ_{2}^{*}) p_{v} - (μ + n) - (1 - ρ_{1}^{*}) γ_{1} g_{1} U_{1}^{*} + (1 - \frac{ρ_{1}^{*}}{r_{1}}) γ_{2} g_{2} U_{2}^{*}] \\ - τ_{1} [(1 - ρ_{1}^{*}) g_{1} U_{1}^{*}] - τ_{2} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{1} U_{2}^{*}] + τ_{3} [(1 - ρ_{1}^{8}) g_{1} U_{1}^{*}] + τ_{4} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{2} U_{2}^{*}] \end{cases}}$

$τ_{6}^{'} = - 1 {\begin{cases} K_{2} + τ_{6} [(1 - \frac{ρ_{2}^{*}}{r_{2}}) p_{p} - (μ + n) - (1 - ρ_{1}^{*}) γ_{1} g_{1} U_{1}^{*} + (1 - \frac{ρ_{1}^{*}}{r_{1}}) γ_{2} g_{2} U_{2}^{*}] \\ - τ_{1} [(1 - ρ_{1}^{*}) g_{1} U_{1}^{*}] - τ_{2} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{2} U_{2}^{*}] + τ_{3} [(1 - ρ_{1}^{*}) g_{1} U_{1}^{*}] + τ_{4} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{2} U_{2}^{*}] \end{cases}}$

$τ_{7} = - 1 {- δ - τ_{3} h_{1} U_{1}^{* *} - τ_{4} h_{2} U_{2}^{* *} + τ_{7} [\frac{w_{M} (U_{1}^{* *} + U_{2}^{* *})}{(U_{1}^{* *} + U_{2}^{* *}) + H_{w}} - \frac{q_{M} (U_{1}^{* *} + U_{2}^{* *})}{(U_{1}^{* *} + U_{2}^{* *}) + H_{q}} - μ_{M}]}$

and having $τ_{i} (t_{f}) = 0, i = 1, 2, .., 7$ as transversality conditions. Moreover,

$ρ_{1}^{*} (t) = \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t)) + (τ_{2} U_{2}^{*} (t))}, y_{1}}$

and $ρ_{2}^{*} (t) = \min {\max {x_{2}, - \frac{τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7}}{2 L_{2}} \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{3}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}}, y_{2}}$ .

Proof: The fact that the adjoint equations and transversality conditions as stated by the theorem are standard results from Pontryagin’s maximum principle.^20,31 we obtain the adjoint system by differentiating the given Lagrangian with respect to state variables $U_{1}, U_{2}, U_{1}^{*}, U_{2}^{*}, V, P$ and M as follows:

$τ_{1}^{'} = - \frac{\partial L}{\partial U_{1}} = - 1 {\begin{cases} τ_{1} [- α_{1} - (1 - ρ_{1}^{*}) g_{1} (V^{*} + P^{*})] + τ_{3} [(1 - ρ_{1}^{*}) g_{1} (V^{*} + P^{*})] \\ + τ_{5} [(1 - ρ_{1}^{*}) γ_{1} g_{1} V^{*}] + τ_{6} [(1 - ρ_{1}^{*}) γ_{1} g_{1} P^{*}] \end{cases}}$

$τ_{2}^{'} = - \frac{\partial L}{\partial U_{2}} = - 1 {\begin{cases} τ_{2} [- α_{2} - (1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{2} (V^{*} + P^{*})] + τ_{4} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{2} (V^{*} + P^{*})] \\ + τ_{5} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) γ_{2} g_{2} V^{*}] + τ_{6} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) γ_{2} g_{2} P^{*}] \end{cases}}$

$τ_{3}^{'} = - \frac{\partial L}{\partial U_{1}^{*}} = - 1 {τ_{3} (- μ - h_{1} M^{*}) + τ_{7} (\frac{w_{M} M H_{w}}{{(U_{1}^{*} + U_{2}^{*} + H_{w})}^{2}} - \frac{q_{M} M H_{q}}{{(U_{1}^{*} + U_{2}^{*} + H_{q})}^{2}})}$

$τ_{4}^{'} = - \frac{\partial L}{\partial U_{2}^{*}} = - 1 {τ_{4} (- μ - h_{2} M^{*}) + τ_{7} (\frac{w_{M} M H_{w}}{{(U_{1}^{*} + U_{2}^{*} + H_{w})}^{2}} - \frac{q_{M} M H_{q}}{{(U_{1}^{*} + U_{2}^{*} + H_{q})}^{2}})}$ (14)

$τ_{5}^{'} = - \frac{\partial L}{\partial V} = - 1 {\begin{cases} K_{1} + τ_{5} [(1 - ρ_{2}^{*}) p_{v} - (μ + n) - (1 - ρ_{1}^{*}) γ_{1} g_{1} U_{1}^{*} + (1 - \frac{ρ_{1}^{*}}{r_{1}}) γ_{2} g_{2} U_{2}^{*}] \\ - τ_{1} [(1 - ρ_{1}^{*}) g_{1} U_{1}^{*}] - τ_{2} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{1} U_{2}^{*}] + τ_{3} [(1 - ρ_{1}^{*}) g_{1} U_{1}^{*}] + τ_{4} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{2} U_{1}^{*}] \end{cases}}$

$τ_{6}^{'} = - \frac{\partial L}{\partial P} = - 1 {\begin{cases} K_{2} + τ_{6} [(1 - \frac{ρ_{2}^{*}}{r_{2}}) p_{P} - (μ + n) - (1 - ρ_{1}^{*}) γ_{1} g_{1} U_{1}^{*} + (1 - \frac{ρ_{1}^{*}}{r_{1}}) γ_{2} g_{2} U_{2}^{*}] \\ - τ_{1} [(1 - ρ_{1}^{*}) g_{1} U_{1}^{*}] - τ_{2} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{2} U_{2}^{*}] + τ_{3} [(1 - ρ_{1}^{*}) g_{1} U_{1}^{*}] + τ_{4} [(1 - \frac{ρ_{1}^{*}}{r_{1}}) g_{2} U_{2}^{*}] \end{cases}}$

$τ_{7} = - \frac{\partial L}{\partial M} = - 1 {- δ - τ_{3} h_{1} U_{1}^{* *} - τ_{4} h_{2} U_{2}^{* *} + τ_{7} [\frac{w_{M} (U_{1}^{* *} + U_{2}^{* *})}{(U_{1}^{* *} + U_{7}^{* *}) + H_{w}} - \frac{q_{M} (U_{1}^{* *} + U_{2}^{* *})}{(U_{1}^{* *} + U_{2}^{* *}) + H_{q}} - μ_{M}]}$ .

This gives the optimality equations of the system as: $\frac{\partial L}{\partial ρ_{1}} = - 2 L_{1} ρ_{1}^{*} (t) + τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t) - q_{11} (t) + q_{12} (t) = 0$ at $ρ_{1}^{*}$

$\frac{\partial L}{\partial ρ_{2}} = - 2 L_{1} ρ_{2}^{*} (t) + (τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7}) [\frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}]$

$- q_{11} (t) + q_{12} (t) = 0$ at $ρ_{2}^{*}$ .

Hence, we obtain the optimality control $ρ_{1}^{*}$ and $ρ_{2}^{*}$ as

$ρ_{1}^{*} = \frac{1}{2 L_{1}} [τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t) - q_{11} (t) + q_{12} (t)]$ (15)

$ρ_{2}^{*} = \frac{1}{2 L_{1}} [(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7}) \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)]} - q_{21} (t) + q_{22} (t)]$ (16)

It follows from the boundedness on the controls that

$ρ_{1}^{*} = {\begin{matrix} \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t)) & i f & x_{1} < \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t)) < y_{1} \\ x_{1} & i f & \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t)) \leq x_{1} \\ y_{1} & i f & \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t)) \geq y_{1} \end{matrix}$ .

Compatibly, we rewrite $ρ_{1}^{*} (t)$ as: $ρ_{1}^{*} (t) = \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}$ .

The corresponding expression for $ρ_{2}^{*}$ is derived as:

$ρ_{2}^{*} = {\begin{matrix} \begin{array}{l} - \frac{(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7})}{2 L_{2}} . \\ \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)]} \end{array} & i f & \begin{matrix} x_{2} < - \frac{(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7})}{2 L_{2}} . \\ \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)]} < y_{2} \end{matrix} \\ x_{2} & i f & \begin{matrix} - \frac{(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7})}{2 L_{2}} . \\ \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)]} \leq x_{2} \end{matrix} \\ y_{2} & i f & \begin{matrix} - \frac{(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{3})}{2 L_{2}} . \\ \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)]} \geq y_{2} \end{matrix} \end{matrix}$

and having it compact form as:

$ρ_{2}^{*} (t) = \min {\max {x_{2}, \begin{matrix} - \frac{(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7})}{2 L_{2}} . \\ \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)]} \end{matrix}}, y_{2}}$

So, we have shown that the optimality control system is defined by the state system couple with adjoint system and the initial transversality conditions together with properties of the optimal control for PMC treatment deduced as: $ρ_{1}^{*} (t) = \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}$ (17)

$ρ_{2}^{*} (t) = \min {\max {x_{2}, \begin{matrix} - \frac{(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7})}{2 L_{2}} . \\ \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)]} \end{matrix}}, y_{2}}$ (18)

Therefore, a complete optimality control system is thus, derive by the substitution of (17) and (18) into the original model equations (1)–( 7) and (14) of the adjoint variables i.e.

$U_{1}^{'} = b_{1} - α_{1} U_{1} - [1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}] g_{1} (V + P) U_{1}$

$U_{2}^{'} = b_{2} - α_{2} U_{2} - [1 - \frac{\min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}}{r_{1}}] g_{2} (V + P) U_{2}$

$U_{1}^{*}^{'} = [1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}] g_{1} (V + P) U_{1} - μ U_{1}^{*} - h_{1} M U_{1}^{*}$

$U_{2}^{*}^{'} = [1 - \frac{\min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}}{r_{1}}] g_{2} (V + P) U_{2} - μ U_{2}^{*} - h_{2} M U_{2}^{*}$

$V^{'} = [1 - \min {\max {x_{2}, \begin{matrix} - \frac{(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7})}{2 L_{2}} . \\ \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)]} \end{matrix}}, y_{2}}] p_{p} V$

$\begin{array}{l} - (μ + n) V - [(1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}) γ_{1} g_{1} U_{1} \\ + (1 - \frac{\min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}}{r_{1}}) γ_{2} g_{2} U_{2}] V \end{array}$

$P^{'} = [1 - \frac{\min {\max {x_{2}, \begin{matrix} - \frac{(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7})}{2 L_{2}} . \\ \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)]} \end{matrix}}, y_{2}}}{r_{2}}] p_{p} P$

$\begin{array}{l} - (μ + n) P - [(1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}) γ_{1} g_{1} U_{1} \\ + (1 - \frac{\min {\max {x_{2}, \begin{matrix} - \frac{(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7})}{2 L_{2}} . \\ \frac{U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)}{(C_{1} + C_{2} + C_{3}) [U_{1}^{* *} (t) + U_{2}^{* *} (t) + V^{*} (t) + P^{*} (t) + M^{*} (t)]} \end{matrix}}, y_{2}}}{r_{2}}) γ_{2} g_{2} U_{2}] P \end{array}$

$M^{'} = b_{M} + \frac{w_{M} (U_{1}^{*} + U_{2}^{*})}{(U_{1}^{*} + U_{2}^{*}) + H_{w}} M - \frac{q_{M} (U_{1}^{*} + U_{2}^{*})}{(U_{1}^{*} + U_{2}^{*}) + H_{q}} M - μ_{M} M$

$τ_{1}^{'} = - 1 {τ_{1} [- α_{1} - (1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}) g_{1} (V^{*} + P^{*})]$

$\begin{array}{l} + τ_{3} [(1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}) g_{1} (V^{*} + P^{*})] \\ + τ_{5} [(1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}) γ_{1} g_{1} V^{*}] \\ + τ_{6} [(1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (τ_{1} U_{1}^{*} (t) + τ_{2} U_{2}^{*} (t))}, y_{1}}) γ_{1} g_{1} P^{*}]} \\ . \\ . \\ . \\ τ_{7} = - 1 {- δ - τ_{3} h_{1} U_{1}^{* *} - τ_{4} h_{2} U_{2}^{* *} + τ_{7} [\frac{w_{M} (U_{1}^{* *} + U_{2}^{* *})}{(U_{1}^{* *} + U_{2}^{* *}) + H_{w}} - \frac{q_{M} (U_{1}^{* *} + U_{2}^{* *})}{(U_{1}^{* *} + U_{2}^{* v}) + H_{q}} - μ_{M}]} (19) \end{array}$

with $τ_{i} (t_{f}) = 0$ , $i = 1, ....., 7$ , $U_{1} (0) = U_{(1)}_{^{0}}, U_{2} (0) = U_{(2)}_{0}, U_{1}^{*} (0) = U_{_{{_{(1)}}_{^{^{^{^{0}}}}}}}^{*}, U_{2}^{*} (0) = U_{_{(2)}}^{*}_{0}, V (0) = V_{0},$ $P (0) = P_{0}$ and $M (0) = M_{0}$ .

Uniqueness of optimality control system

We complete this section with a simple proof of the uniqueness of solution of the optimality system for a small time interval. Achieving this, we explore the following theorem, which takes it leap from the lemma below.

Lemma 3.1: The function $ρ^{*} (z) = (\min (\max (z, x), y))$ is Lipschitz continuous in z where $x < y$ are some fixed positive constants.

Theorem 3.3. Let time interval $t_{f}$ be sufficiently small, then bounded solutions of the optimality system are unique.

Proof: Given that $(U_{1}, U_{2}, U_{1}^{*}, U_{2}^{*}, V, P, M, τ_{1}, τ_{2}, τ_{3}, τ_{4}, τ_{5}, τ_{6}, τ_{7})$ and

$({\bar{U}}_{1}, {\bar{U}}_{2}, {\bar{U}}_{1}^{*}, {\bar{U}}_{2}^{*}, \bar{V}, \bar{P}, \bar{M}, {\bar{τ}}_{1}, {\bar{τ}}_{2}, {\bar{τ}}_{3}, {\bar{τ}}_{4}, {\bar{τ}}_{5}, {\bar{τ}}_{6}, {\bar{τ}}_{7})$ are two solutions of our optimality system (19). Then, the value for each of the solutions can be define by letting

$\begin{array}{l} U_{1} = g^{τ t} e, U_{2} = g^{τ t} f, U_{1}^{*} = g^{τ t} h, U_{2}^{*} = g^{τ t} i, V = g^{τ t} j, P = g^{τ t} k, M = g^{τ t} l, \\ τ_{1} =, g^{τ t} m, τ_{2} = g^{τ t} p, τ_{3} = g^{τ t} q, τ_{4} = g^{τ t} r, τ_{5} = g^{τ t} s, τ_{6} = g^{τ t} t, τ_{7} = g^{τ t} u \end{array}$ and

$\begin{array}{l} {\bar{U}}_{1} = g^{τ t} \bar{e}, {\bar{U}}_{2} = g^{τ t} \bar{f}, {\bar{U}}_{1}^{*} = g^{τ t} \bar{h}, {\bar{U}}_{2}^{*} = g^{τ t} \bar{i}, \bar{V} = g^{τ t} \bar{j}, \bar{P} = g^{τ t} \bar{k}, \bar{M} = g^{τ t} \bar{l}, \\ {\bar{τ}}_{1} =, g^{τ t} \bar{m}, {\bar{τ}}_{2} = g^{τ t} \bar{p}, {\bar{τ}}_{3} = g^{τ t} \bar{q}, {\bar{τ}}_{4} = g^{τ t} \bar{r}, {\bar{τ}}_{5} = g^{τ t} \bar{s}, {\bar{τ}}_{6} = g^{τ t} \bar{t}, {\bar{τ}}_{7} = g^{τ t} \bar{u} \end{array}$ where $τ > 0$ is chosen. Furthermore, we let $ρ_{1}^{*} (t) = \min {\max {x_{1}, \frac{1}{2 L_{1}} (m e + p f)}, y_{1}}$

$ρ_{2}^{*} (t) = \min {\max {x_{2}, \begin{matrix} - \frac{(τ_{3} + τ_{4} + τ_{5} + τ_{6} + τ_{7})}{2 L_{2}} . \\ \frac{h + i + j + k + l}{(C_{1} + C_{2} + C_{3}) [g^{τ t} h + g^{τ t} i + g^{τ t} j + g^{τ t} k + g^{τ t} l]} \end{matrix}}, y_{2}}$ and

${\bar{ρ}}_{1}^{*} (t) = \min {\max {x_{1}, \frac{1}{2 L_{1}} (\bar{m} \bar{e} + \bar{p} \bar{f})}, y_{1}}$

${\bar{ρ}}_{2}^{*} (t) = \min {\max {x_{2}, \begin{matrix} - \frac{({\bar{τ}}_{3} + {\bar{τ}}_{4} + {\bar{τ}}_{5} + {\bar{τ}}_{6} + {\bar{τ}}_{7})}{2 L_{2}} . \\ \frac{\bar{h} + \bar{i} + \bar{j} + \bar{k} + \bar{l}}{(C_{1} + C_{2} + C_{3}) [g^{τ t} \bar{h} + g^{τ t} \bar{i} + g^{τ t} \bar{j} + g^{τ t} \bar{k} + g^{τ t} \bar{l}]} \end{matrix}}, y_{2}}$ .

Then, we substitute $U_{1} = g^{τ t} e$ and all corresponding terms into first ODE of equation (19) and differentiate to obtain $e^{'} + τ e = b_{1} - α_{1} g^{τ t} e - [1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (m e + p f)}, y_{1}}] g_{1} g^{τ t} e (j + k)$ . Similarly, for $U_{2} = g^{τ t} f$ and substituting for $U_{1}^{*}, U_{2}^{*}, V, P, M, τ_{1}, ....., τ_{7}$ into their respective ODEs of equation (19), we obtain

$f^{'} + τ f = b_{2} - α_{2} g^{τ t} f - [1 - \frac{\min {\max {x_{1}, \frac{1}{2 L_{1}} (m e + p f)}, y_{1}}}{r_{1}}] g_{1} g^{τ t} e (j + k)$

$h^{'} + τ h = [1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (m e + p f)}, y_{1}}] g_{1} g^{τ t} e (j + k) - u g^{τ t} h - h_{1} g^{τ t} (l h)$

$\begin{array}{l} i^{'} + τ i = [1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (m e + p f)}, y_{1}}] g_{2} g^{τ t} f (j + k) - u g^{τ t} i - h_{2} g^{τ t} (l i) \\ . \\ . \\ . \\ l^{'} + τ l = b_{M} + \frac{w_{M} g^{τ t} (h + i) l}{g^{τ t} (h + i) + H_{w}} - \frac{q_{M} g^{τ t} (h + i) l}{g^{τ t} (h + i) + H_{q}} - μ_{M} g^{τ t} l \end{array}$

$m^{'} + τ m = - 1 {g^{τ t} m [- α_{1} - (1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (m e + p f)}, y_{1}}) g_{1} g^{τ t} (j + k)]$

$\begin{array}{l} + g^{τ t} q [(1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (m e + p f)}, y_{1}}) g_{1} g^{τ t} (j + k)] \\ + g^{τ t} s [(1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (m e + p f)}, y_{1}}) γ_{1} g_{1} g^{τ t} j] \\ - g^{τ t} t [(1 - \min {\max {x_{1}, \frac{1}{2 L_{1}} (m e + p f)}, y_{1}}) γ_{1} g_{1} g^{τ t} k]} \\ . \\ . \\ . \\ u^{'} + τ u = - 1 {- δ - h_{1} g^{τ t} (q h) - h_{2} g^{τ t} (r i) + g^{τ t} (\frac{w_{M} g^{τ t} (h + i) l}{g^{τ t} (h + i) + H_{w}} - \frac{q_{M} g^{τ t} (h + i) l}{g^{τ t} (h + i) + H_{q}} - μ_{M})} . (20) \end{array}$

Next, we perform subtraction of state solution $U_{1}$ from ${\bar{U}}_{1}$ , $U_{2}$ from ${\bar{U}}_{2}$ , …. $M$ , from $\bar{M}$ , $τ_{1}$ from ${\bar{τ}}_{1}$ ,…… $τ_{7}$ , from ${\bar{τ}}_{7}$ . Then, we multiply the solution obtain by appropriate difference of functions and integrate from to . Finally, we proceed to sum all the fourteen integral equations and using estimation approach, we derive the uniqueness of the model solution. Invoking lemma 3.1, we obtain our first result as: $| ρ_{1}^{*} (t) - {\bar{ρ}}_{1}^{*} (t) | \leq \frac{1}{2 L_{1}} | (m e - \bar{m} \bar{e}) + (p f - \bar{p} \bar{f}) |$ and

$| ρ_{2}^{*} (t) - {\bar{ρ}}_{2}^{*} (t) | \leq | \frac{1}{2 L_{2}} [\frac{(q + r + s + t + u) (h + i + j + k + l)}{(C_{1} + C_{2} + C_{3}) g^{τ t} (h + i + j + k + l)} - \frac{(\bar{q} - \bar{r} - \bar{s} - \bar{t} - \bar{u}) (\bar{h} + \bar{i} + \bar{j} + \bar{k} + \bar{l})}{(C_{1} + C_{2} + C_{3}) g^{τ t} (\bar{h} + \bar{i} + \bar{j} + \bar{k} + \bar{l})}] |$ $| ρ_{2}^{*} (t) - {\bar{ρ}}_{2}^{*} (t) | \leq | \frac{1}{2 L_{2}} [\frac{(q + r + s + t + u) (h + i + j + k + l)}{(C_{1} + C_{2} + C_{3}) g^{τ t} (h + i + j + k + l)} - \frac{(\bar{q} - \bar{r} - \bar{s} - \bar{t} - \bar{u}) (\bar{h} + \bar{i} + \bar{j} + \bar{k} + \bar{l})}{(C_{1} + C_{2} + C_{3}) g^{τ t} (\bar{h} + \bar{i} + \bar{j} + \bar{k} + \bar{l})}] |$

$\leq \frac{1}{2 L_{2}} | \frac{\begin{array}{l} (C_{1} + C_{2} + C_{3}) [(q + r + s + t + u) (h + i + j + k + l) - (\bar{q} - \bar{r} - \bar{s} - \bar{t} - \bar{u})] \\ + g^{τ t} [(q + r + s + t + u) - (\bar{q} + \bar{r} + \bar{s} + \bar{t} + \bar{u}) \end{array}}{[(C_{1} + C_{2} + C_{3}) g^{τ t} (h + i + j + k + l)] [(C_{1} + C_{2} + C_{3}) g^{τ t} (\bar{h} + \bar{i} + \bar{j} + \bar{k} + \bar{l})]} | .$

The explicit illustration of the estimate, which use $| ρ_{1}^{*} - {\bar{ρ}}_{1}^{*} |$ estimate, is given for $U_{1} (t)$ as follows:

$\frac{1}{2} {(e - e)}^{2} (t_{f}) + τ_{1} \int_{t_{0}}^{t_{f}} {(e - e)}^{2} d t \leq \int_{t_{0}}^{t_{f}} α_{1} | e - \bar{e} | d t + [\int_{t_{0}}^{t_{f}} | ρ_{1}^{*} e - {\bar{ρ}}_{1}^{*} \bar{e} | | e - \bar{e} | d t] g_{1} + \int_{t_{0}}^{t_{f}} g^{τ t} | (j + k) - (\bar{j} + \bar{k}) | | e - \bar{e} | d t$

$\leq \int_{t_{0}}^{t_{f}} α_{1} | e - \bar{e} | d t + g_{1} [\int_{t_{0}}^{t_{f}} | ρ_{1}^{*} e - {\bar{ρ}}_{1}^{*} \bar{e} | | e - \bar{e} |] d t + \int_{t_{0}}^{t_{f}} g^{τ t} | (j + k) - (\bar{j} + \bar{k}) | | e - \bar{e} | d t$

$\leq Z_{1} \int_{t_{0}}^{t_{f}} [{| e - \bar{e} |}^{2} + {| m - \bar{m} |}^{2} + {| f - \bar{f} |}^{2} + {| p - \bar{p} |}^{2}] d t$

$+ Z_{2} g^{τ t_{f}} \int_{t_{0}}^{t_{f}} [{| e - \bar{e} |}^{2} + {| m - \bar{m} |}^{2} + {| f - \bar{f} |}^{2} + {| p - \bar{p} |}^{2}] d t$ ,

where $Z_{1}$ and $Z_{2}$ are constants evaluated by the coefficients and bounds on states and adjoints of the optimality control system. Combining these fourteen estimates yields the following result:

$\frac{1}{2} {(e - \bar{e})}^{2} (t_{f}) + \frac{1}{2} {(f - \bar{f})}^{2} (t_{f}) + \frac{1}{2} {(h - \bar{h})}^{2} (t_{f}) + \frac{1}{2} {(i - \bar{i})}^{2} (t_{f}) + \frac{1}{2} {(j - \bar{j})}^{2} (t_{f}) + \frac{1}{2} {(k - \bar{k})}^{2} (t_{f}) + \frac{1}{2} {(l - \bar{l})}^{2} (t_{f})$

$+ \frac{1}{2} {(m - \bar{m})}^{2} (t_{0}) + \frac{1}{2} {(p - \bar{p})}^{2} (t_{0}) + \frac{1}{2} {(q - \bar{q})}^{2} (t_{0}) + \frac{1}{2} {(r - \bar{r})}^{2} (t_{0}) + \frac{1}{2} {(s - \bar{s})}^{2} (t_{0}) + \frac{1}{2} {(t - \bar{t})}^{2} (t_{0}) + \frac{1}{2} {(u - \bar{u})}^{2} (t_{0})$

$+ τ \int_{t_{0}}^{t_{f}} [\begin{array}{l} (^{e - \bar{e}) 2} + (^{f - \bar{f}) 2} + (^{h - \bar{h}) 2} + (^{i - \bar{i}) 2} + (^{j - \bar{j}) 2} + (^{k - \bar{k}) 2} + (^{l - \bar{l}) 2} \\ + (^{m - \bar{m}) 2} + (^{p - \bar{p}) 2} + (^{q - \bar{q}) 2} + (^{r - \bar{r}) 2} + (^{s - \bar{s}) 2} + (^{t - \bar{t}) 2} + (^{u - \bar{u}) 2} \end{array}] d t$ .

$\leq (Z_{1} + Z_{2} e^{3 t_{f}}) \int_{t_{0}}^{t_{f}} [\begin{array}{l} (^{e - \bar{e}) 2} + (^{f - \bar{f}) 2} + (^{h - \bar{h}) 2} + (^{i - \bar{i}) 2} + (^{j - \bar{j}) 2} + (^{k - \bar{k}) 2} + (^{l - \bar{l}) 2} \\ + (^{m - \bar{m}) 2} + (^{p - \bar{p}) 2} + (^{q - \bar{q}) 2} + (^{r - \bar{r}) 2} + (^{s - \bar{s}) 2} + (^{t - \bar{t}) 2} + (^{u - \bar{u}) 2} \end{array}] d t$

holds for all $t_{0} = 0$

We thus conclude from the above equation that the inequality

$\leq (Z_{1} + Z_{2} e^{3 t_{f}}) \int_{t_{0}}^{t_{f}} [\begin{array}{l} (^{e - \bar{e}) 2} + (^{f - \bar{f}) 2} + (^{h - \bar{h}) 2} + (^{i - \bar{i}) 2} + (^{j - \bar{j}) 2} + (^{k - \bar{k}) 2} + (^{l - \bar{l}) 2} \\ + (^{m - \bar{m}) 2} + (^{p - \bar{p}) 2} + (^{q - \bar{q}) 2} + (^{r - \bar{r}) 2} + (^{s - \bar{s}) 2} + (^{t - \bar{t}) 2} + (^{u - \bar{u}) 2} \end{array}] d t \leq 0$ ,

where $Z_{1}, Z_{2}$ are functions that depend on the coefficients and bounds of $e, f, h, ......, u$ . Therefore, for any chosen value of $(τ)$ , such that $τ > Z_{1} + Z_{2}$ and $t_{f} < \frac{1}{3 τ} \ln (\frac{τ - Z_{1}}{Z_{2}})$ , the expressions

$e = \bar{e}, f = \bar{f}, h = \bar{h}, i = \bar{i}, j = \bar{j}, k = \bar{k}, l = \bar{l}, m = \bar{m}, p = \bar{p}, q = \bar{q}, r = \bar{r}, s = \bar{s}, t = \bar{t}, u - \bar{u}$ holds. Hence, the solution is unique for sufficiently small time.

We refer readers to models.^9,13 for related proofs of uniqueness of optimality control system. Logically, uniqueness for small time interval are conspicuously two–point boundary value problem due to its opposite time orientation and the state equations, which are embedded with initial and final time conditions of the adjoint equations. Furthermore, analysis of Thm. 3.3 shows that if $τ > L_{1} + L_{2}$ and $t_{f} < \frac{1}{3 τ} \ln (\frac{τ - L_{1}}{L_{2}})$ , such that $L_{2} ⊲ 0$ , infectivity is drastically under control and could be below detectable limits of clinical assay. Intuitively, for $t_{f} > \frac{1}{3 τ} \ln (\frac{τ - L_{1}}{L_{2}})$ such that $τ < L_{1} + L_{2}$ , then endemic infectivity prevails, which could assume global dimension. Next, we investigate the optimality control for periodic multiple chemotherapy treatment.

The scope of this study compels us to the design for a more befitting optimal dual HIV–parasitoid pathogen multiple chemotherapy treatment championed by periodic treatment interruptions. This is to say that we aim at establishing optimal control that best describe treatment schedules under on and off chemotherapy, worthy to be considered as periodic multiple chemotherapy method (PMC – M).

Periodic multiple chemotherapy method

Here, let time assume discrete controls for $ρ_{1}$ and $ρ_{2}$ i.e. $t \in [0, y_{i}]$ . The implication is that if control vector is 0, treatment is off and if $t \equiv y_{i} \neq 0$ , treatment is full (i.e. on). Also, if we consider $t \leq 30$ months i.e. $t \leq 900$ days, then vector control limit is $1 \times 30$ months and the set of all such control vectors can be designed as $χ$ . Thus, we’re treating an optimal control vector pair ( $ρ_{1}^{*}, ρ_{2}^{*}$ ) that satisfies $\min_{ρ_{1}, ρ_{2} \in χ} R (ρ_{1}, ρ_{2}) = R (ρ_{1}^{*}, ρ_{2}^{*})$

and subject to the state system (1)–(7), such that $R (ρ_{1}, ρ_{2})$ is defined by (12). The present study varies from other related models.^1,13 where drugs time intervals considered, were on daily administration of drugs. This present study considers drugs administration on weekly intervals taking infection set–point as $[t_{0}, t_{f}] \in [3, 30]$ months.².

Now, if we let $χ$ be the set of elements, then our optimal control pair is satisfied. Furthermore, if a random selection of pair elements is made from this set $χ$ , then we can solve the state system using these controls pair. This procedure is repeated for all possible pairs and then choose the value of the objective functional, $ℜ$ , with the smallest cost functional value as the optimal control value pair, $ρ_{1}^{*}$ and $ρ_{2}^{*}$ . The outcome of this process is obviously cumbersome and thus, lead to complex cost benefit evaluation for state system (1)–(7).

Moreso, retaining the time interval $t \in [3, 30]$ months, the periodic cost benefit evaluation would be ${(2^{120})}^{2}$ since each control pair is $1 (w e e k) \times 30 (m o n t h s)$ vectors, a procedure that is comparatively expensive. So, we could design a more probable iterative process with simpler and shorter computations. Again, we consider 2 weeks segments as against 1 week. This seems more convenient and practicable for the fact that keeping to treatment schedules of highly docile clinical drugs of this magnitude, daily observation is almost not feasible. Therefore, for 2 weeks segments, the complexity for each control pair is reduced to 1*14 from 1*30. The reduced number of iterations is thus ${(2^{14})}^{2}$ , which still looks large.

Further simplification leads to the consideration of subperiods of such given period i.e. $[0, 4], [0, 8], [0, 12], ..., [0, 120]$ , a procedure that accounts and lessen the burden of earlier approach but are similar in technique to that by.^1,13,23 where only single infection was considered respectively. For easy assimilation, we call this approach, “multiple periodic methods”. A method built upon an optimal PMC control pair $(ρ_{1}^{*}, ρ_{2}^{*})$ , for a step–wise reducible iteration technique with 2 weeks segments from the first MP method $[0, 4]$ . The implication is that the magnitude of $ρ_{1, 1}^{*}$ and $ρ_{1, 2}^{*}$ is $1 \times 4$ (for weekly segment of 1 month), so the optimal solution is obtain as ${(2^{4})}^{2} = 256$ iterations as against ${(2^{6})}^{2} = 4096$ iterations from.¹ and $2^{10} = 1024$ iterations from.²³ For next period of $[0, 8]$ , the control pair is

$ρ_{2, 1}^{*} = [ρ_{1, 1}^{*}, \land, \land, \land, \land, \land]$ and $ρ_{2, 2}^{*} = [ρ_{1, 2}^{*}, \land, \land, \land, \land, \land]$ , where $\land$ is 0 or $y_{i}$ .

The explicit procedure is that we take $[0, 4]$ optimal PMC control pair $ρ_{1, 1}^{*}$ and $ρ_{1, 2}^{*}$ as the first 4 elements of the controls $ρ_{2, 1}$ $ρ_{2, 1}^{*}$ and $ρ_{2, 2}^{*}$ respectively. Then, we iterate $ρ_{2, 1}$ and $ρ_{2, 2}$ to obtain the next optimal MPC control pair ( $ρ_{2, 1}^{*}$ , $ρ_{2, 2}^{*}$ ) over $[0, 8]$ period, which also give ${(2^{4})}^{2} = 256$ iterations. The process is repeated for each of the control pair for the time intervals up to $[0, 120]$ . The PMC control vectors obtained for the entire iterations are $[0, 120]$ and $ρ_{2}^{*} = ρ_{4, 2}^{*}$ , which clearly represents a suboptimal model.

This later technique is an enhanced and extended approach of the models.^1,23 which establishes the intermittent (or periodic) application of multiple drugs as a means of controls of drugs severities and maximization of healthy T–lymphocytes cells and macrophages with structured treatment interruption after a prolong chemotherapy administration. From these two models, it is observed that though T–lymphocytes cells and macrophages were maximized, thereby prolonging the life–span of infected patients as well as suppression of viral load, these virions were not completely eliminated. Thus, re–emergence of infection is likely to occur. Therefore, we decisively omits the numerical simulations of our later method, which will also yield an improve result when compared to models.^1,23 but definitely not leading to the elimination of viral load and parasitoid–pathogen.

On the other hand, cases abound where due to either lack of availability of drugs for smooth continuity or bored by continuous administration of drugs and in most situations drug side–effects become a constraint for practical optimal continuous application of chemotherapies. Furthermore, chemotherapy observations and alternations require time intervals. This leads to the formulation of optimal control for periodic multiple chemotherapy (PMC) treatment.

Numerical computation: continuous case with no control measures

At this moment, we are obliged to show that optimality system is a two–point boundary value problem. Therefore, we first simulate the state system (1)–(7), using initial conditions as specified by (Table 1 & 2) above. This stage of numerical illustrations shows the interactive behavior of state variables following multiple applications of chemotherapies without optimal control measures on the chemotherapies. Here, we intend to appreciate the model when no controls measures are imposed on treatment factors and thus, having no access to control the systemic cost. The second stage is the methodological application of multiple chemotherapies for the maximization of T–lymphocytes cells and macrophages; and minimization of the systemic cost following the implementation of state adjoint system and transversality conditions. The optimal controls, can then be updated to choice treatment for each iteration using drugs efficacy control formulas (17) and (18) until convergence is attained.

To initiate our simulation, we invoke treatment compactible period from model.¹⁷ such that $t \in {3, 30}$ months (i.e. $\leq 900$ days), which accounts for drug validity period. So, for early perturbation of uninfected cells by introduction of dual virions per $m m^{3}$ blood plasma, and taking initial values as in Tables 1 & 2, we demonstrate as depicted by Figure 2a–g below, the methodological application of multiple chemotherapy with complete zero optimal control measures, satisfying aims (i), (ii) and (iv) of the study. Thus, for a continuous multiple chemotherapy with two treatment (without optimal control measures and penalty conditions, $ρ_{1}^{*}$ and $ρ_{2}^{*}$ ) factors, we observe for: (i) $ρ_{1} = 0.5$ , which acts on $U_{1}, U_{2}, U_{1}^{*}$ and $U_{2}^{*}$ , that Figure 2a exhibits gradual inclination (or maximization) of uninfected T–lymphocytes (CD4⁺ T cell count) concentration from its initial value of $U_{1} = 0.4$ $c e l l s / m m^{3}$ to an overwhelming $U_{1} = 2.256 \times 10^{3}$ $c e l l s / m m^{3}$ for $t \leq 30$ months. This outcome is enhanced by the presence of the high immune effectors response $(M)$ , which is boosted by RTI.

Figure 2b represents the simulation of uninfected macrophages under the same action of RTI. Healthy macrophages is maximized from its initial value of $U_{2} = 0.2$ $c e l l s / m m^{3}$ to an increase volume $U_{2} = 451.36$ $c e l l s / m m^{3}$ , which strongly again, indicate the effect of the presence of immune effectors response.

Furthermore, Figure 2c depicts behavioral infectivity of infected T–lymphocytes (CD4⁺ T cell count), following the application of RTI in the presence of high immune effectors response. Here, infected T–lymph cells with initial value $U_{1}^{*} = 0.1$ , exhibited early growth to a value $U_{1}^{*} = 0.327$ , through the first 7 months but declined thereafter to the value $U_{1}^{*} = 0.027$ following continuous medication and the presence of high immune effectors response. Infected macrophages cells declined to a negligible value of $U_{2}^{*} = 0.022$ in the interval $10 \leq t \leq 30$ months. The high concentration of healthy T–lymphocytes in Figure 2a, attest to this latter result. A critical view of Figure 2d, depicts an overwhelming decline of infected macrophages cells, which exhibits undulating negative trend at the 7^th month. We as well, observe gradual re–emergence with stability at zero after 30 months of chemotherapy (RTI) in the presence of boosted immune effectors response.

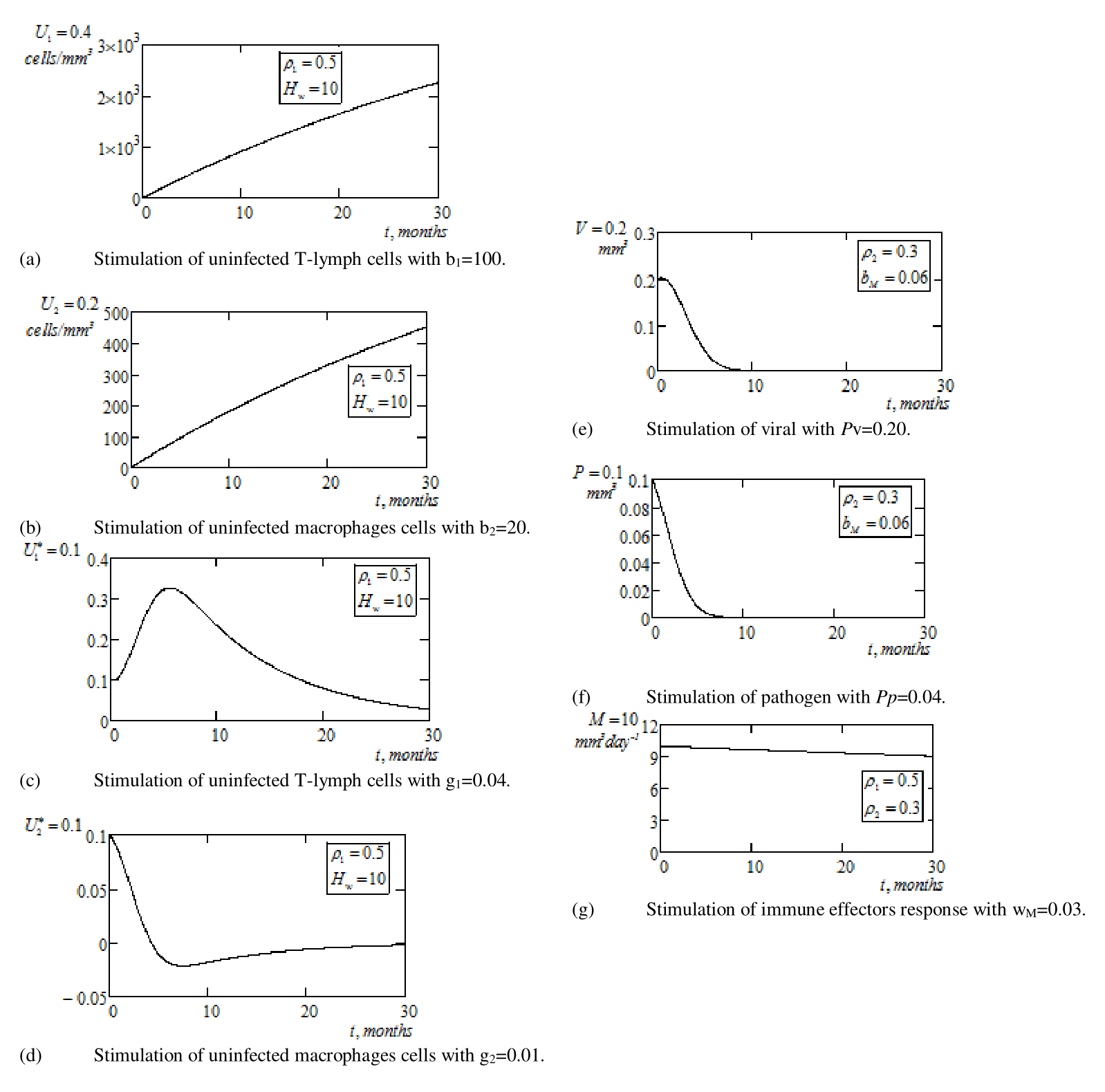
Figure 2 Graphical simulations of continuous optimal multiple chemotherapy treatment without optimal control measures and penalty conditions, and penalty conditions, ρ^*₁and ρ^*₂.

On the other hand, the second chemotherapy (PIs), i.e. (ii) $ρ_{1} = 0.3$ , which predominantly act on virions viral load and parasitoid– pathogen is use to study the biological behavior of these virions in the presence of boosted immune effectors response. Figure 2e depicts eventual elimination of viral load after 9 months of continuous application of treatment measure with high immune effectors response. We see a viral load of initial value of $V = 0.202$ $m m^{3}$ decline and eliminated to zero after 9 months. Also, the attack of PIs on parasitoid pathogen is depicted by Figure 2f. The outcome is the sharp decline and eventual elimination pathogen after 8 months of continuous PIs chemotherapy.

Finally, Figure 2g represents the biological behavior of immune effectors response, which is boosted by the introduction of multiple chemotherapies (RTI and PIs). Immune effectors response has the essential components, which play critical role of antiviral defense as it attack the virions, thereby increasing the concentration of healthy T–lymphocytes cells and macrophages. The decline of immune effectors response from ( $10 \to 9$ ) $m m^{3} d a y^{- 1}$ is a clear indication of deduction of virions and clearance rate due to attack on both infected cells. In other words, the concentration/increase of immune effectors response in the CD4⁺ T cells is a function of the amount of virions presence (or virus’s rate of attack on the immune system).

Now, we have seen that the results of the numerical simulations for continuous application of multiple chemotherapies without optimal control measures on treatment factors for a dual HIV–parasitoid pathogen as significantly beneficial to the maximization of both healthy T–lymphocytes and macrophages cells; and boosted immune effectors response, suppresses/reduced viral load and pathogens. The constraints of this result are the inability of the initial state system (1)–(7) to define treatment cost at this level. On this note, we opt to investigate the case for continuous multiple chemotherapy treatment (MCT) with control measures (bounds) on the optimal weight factors of $ρ_{1}^{*}$ and $ρ_{2}^{*}$ (RTIs and PIs). This approach is hoped to be more rewarding.

Numerical simulation of MCT: continuous case with control measures

Here, observing the state variables and parameter values of Tables 1 & 2, we simulate model (19), which gives us the option to evaluate the cost of treatment. These illustrations account for any possible drug side–effect in cognizance with drug validity period, i.e. drug bounds $x_{1} = 0, x_{2} = 0.2, y_{1} = 0.2, y_{2} = 0.8$ . and clinically balance any variations of state variables in the objective functional (12) by the optimal weight factors $K_{1} = 0.1, K_{2} = 20, L_{1} = 2000, L_{2} = 25$ and $δ = 10$ respectively.

Thus depicted by Figure 3a, we investigate the concentration of uninfected T–lymphocytes cells following the application of optimal control measures on RTIs as indicated by $ρ_{1}^{*}$ of equation (17). Furthermore, sustaining Tables 1 & 2 and with the inclusion of the penalty conditions i.e. ${τ_{1}, ......, τ_{7}} = {0.2, 0.2, 0.2, 0.1, 0.2, 0.2, 10}$ , we observe that the concentration of uninfected T–lymphocytes cells experience appreciable increase from $U_{1} (t) = 0.4 \to 2, 256 \times 10^{3}$ $c e l l s / m m^{3}$ , as was the case when treatment was administered without control measures (Figure 2a). The situation implies that maximization of healthy CD4⁺ T cells is independent of prolong chemotherapy application.

From Figure 3b, with the application of control measure (as in $ρ_{1}^{*}$ ), healthy macrophages cells exhibit high concentration at the early months of chemotherapy with stability at ${(10 - 12)}^{t h}$ months having value $U_{2} (t) = 0.2 \to 107.586$ $c e l l s / m m^{3}$ , before declining to $U_{2} (t) = - 143.913$ $c e l l s / m m^{3}$ at 30 months of chemotherapy. The implication is that for maximum restoration of healthy macrophages, chemotherapy most be on short term schedule.

In Figure 3c, we see an enhance minimization/reduction of infected T–lymphocytes cells after initial increase at the early $(0 - 3)$ months. Precisely, infection is seen to decline to $U_{1}^{*} (t) = 0.019$ after 30 months of chemotherapy as against $U_{1}^{*} (t) = 0.027$ of Figure 2c. The enhance decline over that of Figure 2c, can be attributed to the application of optimal controls on chemotherapies. Also, depicted by Figure 3d, is the drastic reduction of infected macrophages to a value $U_{2}^{*} (t) = 0.1 \to 4.453 \times 10^{- 3}$ , following the application of penalty conditions on treatment factors. Here, it is suggested that treatment could be control to avoid early drugs side–effects.

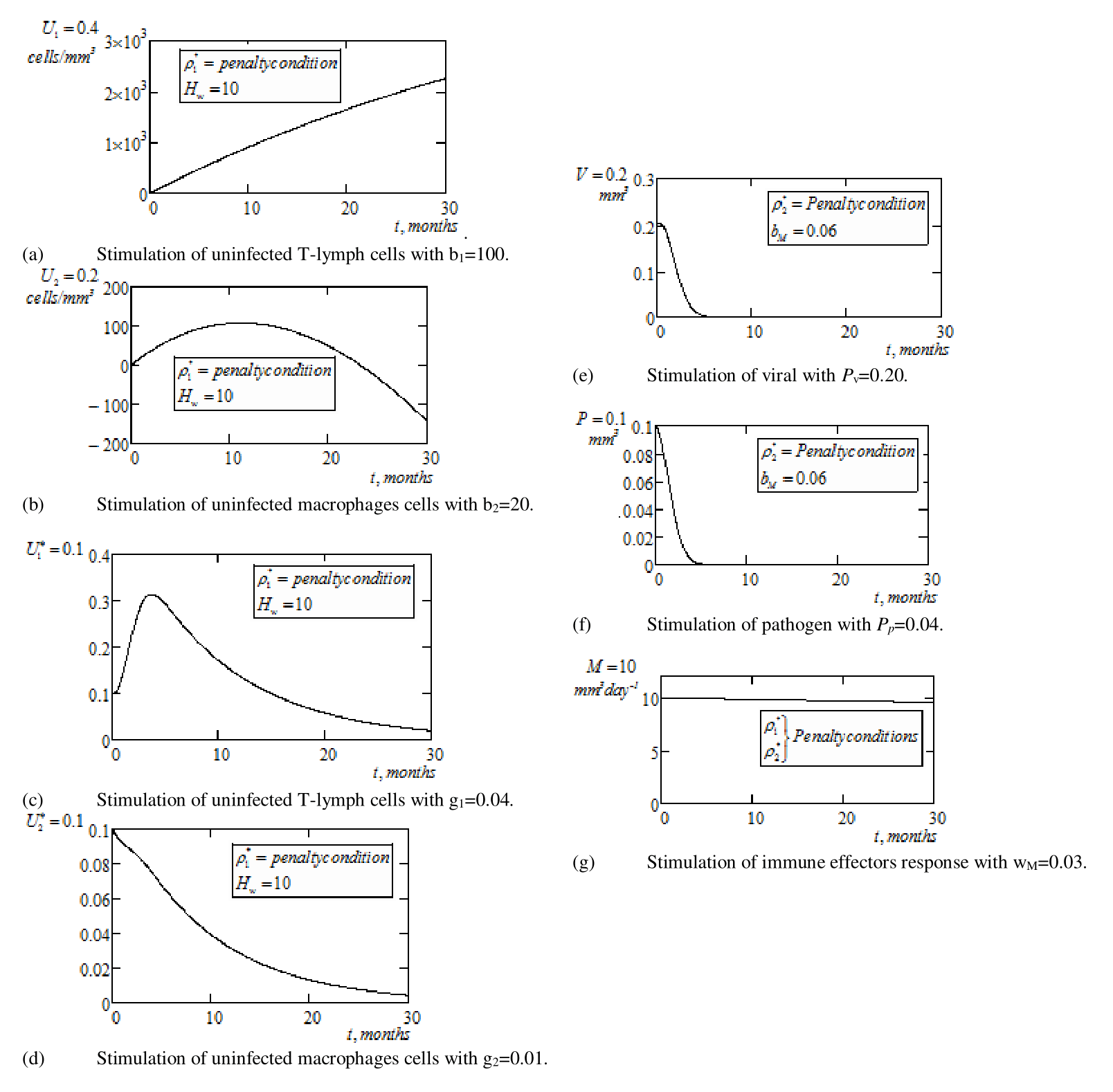
Figure 3 Graphical simulations of continuous optimal multiple chemotherapy treatment with optimal control measures and penalty conditions, ρ^*₁and ρ^*₂.

From Figure 3e, with the application of control measure as in $ρ_{2}^{*}$ of equation (18), we observe sharp decline of viral load, leading to elimination of viral virus to $V (t) = 0$ after 5 months of continuous clinical application of chemotherapy. Result indicates an improvement in the period of elimination compared to when treatment was administered without penalty conditions on drugs (Figure 2e). In a similar condition, Figure 3f depicts elimination of parasitoid pathogen at the $4^{t h}$ month of drug application. The time interval for drugs without control measures was 8 months.

The biological behavior of the immune effectors response is represented as in Figure 3g. Here, immune effectors response boosted by the control measures ( $ρ_{1}^{*}, ρ_{2}^{*}$ ), exhibits stability with minimal loss due to clearance rate at the $ρ_{1}^{*}, ρ_{2}^{*}$ month i.e. $9.86 \leq M (t) \leq 10$ $m m^{3} d a y^{- 1}$ . This shows that immune effectors response is always maintained at a positive level and it is never eliminated. Again, for brevity graphical representations of the penalty conditions are omitted. Figure 4a & 4b below, simulate the optimal control pair $ρ_{1}^{*}$ and $ρ_{2}^{*}$ , with defined lower and upper bounds on the optimal weight factors of RTIs and PIs respectively. Here, we see that the most intriguing indication of Figure 4a & 4b are the smooth continuous MCT–like characteristics of the optimal dynamics. Precisely, Figure 4a shows that with high optimal weight factor on RTIs, balanced by low upper bound of $y_{1} = 0.2$ , the toxicity of the drug lies between $0.5 \leq ρ_{1}^{*} (t) \leq 0.501$ . Similarly, PIs with less optimal weight factor and having higher upper bound of $y_{2} = 0.8$ , exhibits drug toxicity in the interval $0.3 \leq ρ_{2}^{*} (t) \leq 6.3$ .

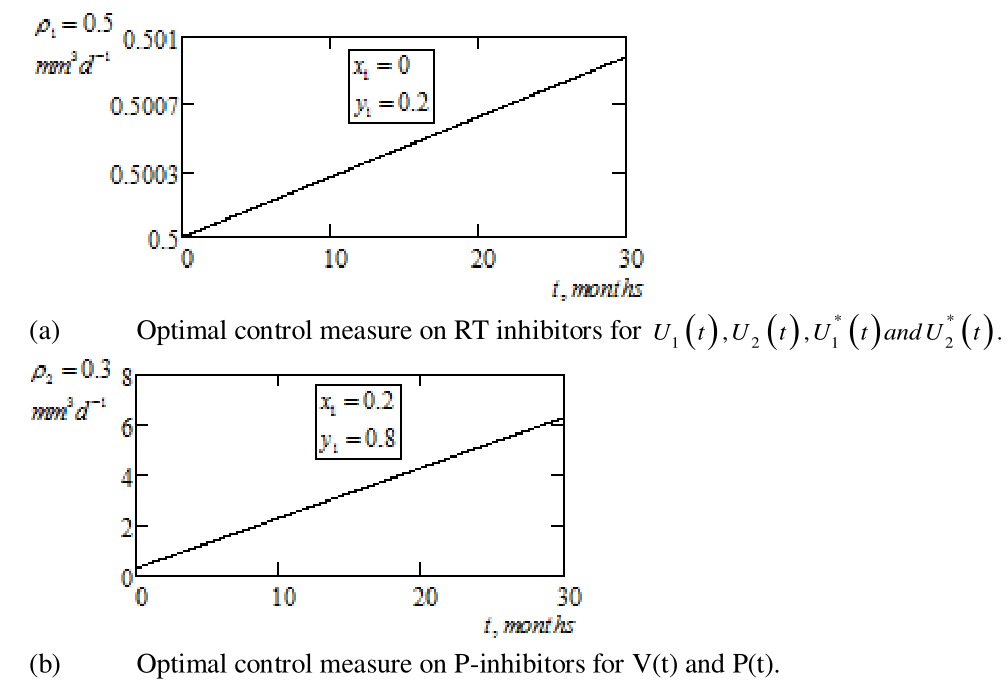
Figure 4 Graphical simulations of optimal control pair for continuous multiple chemotherapy treatment with penalty conditions, $K_{1} = 0.1, K_{2} = 0.2, L_{1} = 2000, L_{2} = 25$ and $δ = 10$ .

This present work carefully identified and formulated using ordinary differential equations a 7 – Dimensional mathematical dual HIV–parasitoid pathogen dynamic model. Unlike most other models with single viral infection as specified in our literature, this present model not only incorporate the investigation of parasitoid–pathogen to HIV infection as dual infectivity, but further introduced as treatment factors, multiple chemotherapy in cognizance of the critical function of enhanced immune effectors response.

The model was presented as an optimal control problem, and classical optimal control theory paradigm was explored for the analysis. Numerical methods was utilized to simulate varying illustrations of the model. For simplicity, the analysis accounted for continuous multiple chemotherapy treatment for dual infections without control measures and penalty conditions on the treatment factors, periodic multiple chemotherapy with control measures on optimal weight factors and continuous multiple chemotherapy treatment with optimal control measures on optimal weight factors and penalty conditions on treatment factors and state variables.

Numerical results indicated that optimal dual chemotherapy treatment of dual HIV–pathogen infection is dynamical to drug toxicity at treatment initiation and is independent of prolong application of chemotherapy. From continuous MCT investigation, uninfected T–lymphocytes cells and macrophages was maximized in concentration, and infectious cells was significantly suppressed (not eliminated) at $t_{f} \leq 30$ months. Viral load and pathogen were eliminated after 9 and 8 months of continuous chemotherapy. The constraint here was the non–quantification of systemic cost due to lack of control measures on optimal weight factors.

Periodic multiple chemotherapy defined discrete treatment of dual infections, the suboptimal model of which controlled drug adversities, prolonged life–span of infected patients without necessarily eliminating virions. This suboptimal model, which had lesser iterative process was an improved approach when compared with other existing related techniques (see literature). Infected cells and viral load were not eliminated but suppressed to supportable levels.

Of note, we observed an intriguing outcome for a continuous application of MCT with compactible optimal control measures on chemotherapy optimal weight factors. Concentration of maximized healthy T–lymphocytes was sustained at its peak value, while uninfected macrophages exhibited increasing trajectory with stability at the (10–12) the months and then declined thereafter to near zero at 30^th month. On the other hand, infected cells were drastically reduced and could possibly be eliminated after $t_{f} \geq 30$ months. Interesting, the time taken to eliminate both viral load and parasitoid–pathogen were relative small i.e. $V (t) = 0$ at $t_{f} \in 5$ months and $P (t) = 0$ at $t_{f} \in 4$ months respectively. Furthermore, this aspect of investigation clearly defined drug toxicity range, which translates to quantifying benefits on treatment cost.

Form experiment 2, healthy macrophages concentration exhibited gradual increase to a maximum of $U_{2} (t) = 451.36$ $m m^{3} d^{- 1}$ at $t_{f} \leq 30$ months. Experiment 3, had macrophages maximum value of $U_{2} (t) = 107.583$ $m m^{3} d^{- 1}$ at $t_{f} 10 - 12$ months and then declined to near zero at $t_{f} \leq 30$ months. The later decline is said to suggest stoppage of further subjection of macrophages to continuous medication. In addition, Figure 3a–g, evaluated the significant of the implementation of optimal control pair with penalty conditions and as well, avail us the opportunity to quantify the amount of control measures on RT inhibitors and PI inhibitors in blocking new infections and killing virions. This aspect, which directly translates to the evaluation of systemic cost benefit on treatment, is an integral part of this study.

Furthermore, viral load and parasitoid–pathogen were successfully eliminated at reduced time intervals following the application of optimal control measures and penalty conditions on treatment factors i.e. $V (t) = 0$ for $t_{f} \leq 5$ months and $P (t) = 0$ for $t_{f} \leq 4$ months respectively. Finally, the presence of immune effectors response boosted by treatment factors played all critical roles in enhancement of high concentration of healthy cells, block new replication of infected cells and eradication of virions. However, the slight decline of immune effectors response as in experiments 2 & 3, justified reduction/eradication of infectious cells and virions and probable immune clearance rate. This is obvious as immune effectors response concentration is a function of virions concentration in the immune systems.

A critical view of Table 3, revealed the dynamic and positive improved variations in the outcome of the final analyses, taking time duration of $t_{f} \leq 30$ months. From the analyses, it is seen that, while healthy T–lymphocytes cells are maximized with no variation for $U_{1} (t) = 0.4 \to 2.256 \times 10^{3}$ $m m^{3} d^{- 1}$ from both experiment 2 & 3, the benefit on treatment cost cannot be evaluated. Experiments 3 & 4, with control measures shows that drug toxicity are measured in the range of $ρ_{1}^{*} (t) = 0.5 \to 0.501$ and $ρ_{2}^{*} (t) = 0.3 \to 6.3$ respectively. This implies that more of PIs with high toxicity is required for effective control/eradication of viral load and pathogen virions.

Expt. $t \underset{⌣}{\overset{⌢}{\leq}} t_{f}$

Monties

$u_{1} (t)$

$u_{2} (t)$

$u {}_{1}^{*}{(t)}$

$u {}_{2}^{*}{(t)}$

$v (t)$

$p (t)$

$m (t)$

$p_{1} (t)$

$p_{2} (t)$

$L_{1}$

$L_{2}$

$x_{1}$

$x_{2}$

$y_{1}$

$y_{2}$

$p {}_{1}^{*}{(t)}$

$p {}_{2}^{*}{(t)}$

2

30

$\begin{array}{l} 2.256 Χ 10^{3} \\ ↑ \\ 0.4 \end{array}$

$\begin{array}{l} 451.36 \\ ↑ \\ 0.2 \end{array}$

$\begin{array}{l} 0.1 \\ ↓ \\ 0.27 \end{array}$

$\begin{array}{l} 0.1 \\ ↓ \\ - 0.027 \end{array}$

$\begin{array}{l} 0.2 \\ ↓ \\ 0 \\ @ \\ 9 m o n t h \end{array}$

$\begin{array}{l} 0.1 \\ ↓ \\ 0 \\ @ \\ 8 m o n t h \end{array}$

$\begin{array}{l} 10 \\ ↓ \\ 9 \end{array}$

$\overset{↗}{0.5}$

$\overset{↗}{0.3}$

0

?

3 & 4

30

$\begin{array}{l} 2.256 Χ 10^{3} \\ ↑ \\ 0.4 \end{array}$

$\begin{array}{l} 107.583 \\ ↑ \\ 0.2 \end{array}$

$\begin{array}{l} 0.1 \\ ↓ \\ .018 \end{array}$

$\begin{array}{l} 0.1 \\ ↓ \\ 4.408 Χ 10^{3} \end{array}$

$\begin{array}{l} 0.2 \\ ↓ \\ 0 \\ @ \\ 5 m o n t h \end{array}$

$\begin{array}{l} 0.1 \\ ↓ \\ 0 \\ @ \\ 4 m o n t h \end{array}$

$\begin{array}{l} 10 \\ ↓ \\ 9.94 \end{array}$

$\overset{↗}{0.5}$

$\overset{↗}{0.3}$

2000

25

0

0.2

0.8

0.501

63

Table 3 Summary of results optimality control system for treatment without and with control measures and penalty conditions
Note: Expt. 4 provided the result for and highlight-state variables, purple-control variable without control measures, orange-optimal weight factors and lower and upper bounds on treatment factors (RTI and PIs) and yellow-optimal control pair with control measures. -increase, -decrease and -varying drug toxicity.

As a penultimate model to those existing models identified in the literature, this paper formulated classical mathematical dynamic model, which accounted for the incorporation of dual HIV–parasitoid pathogen on dual target cells studied under continuous and periodic multiple chemotherapy treatments (RTI and PIs) enhanced by presence of immune effectors response. The model addresses the persistent issues of HIV and its allied infections and treatment progression in three folds: – continuous multiple chemotherapy treatment without optimal control measures on treatment weight factors; – periodic multiple chemotherapy, considered as off and on treatment time interval; and continuous multiple chemotherapy treatment with induced optimal control measures on treatment optimal weight factors.

Results of numerical simulations showed that optimality control strategy without control measures led to the maximization of both healthy T–lymphocytes and macrophages cells, suppression of both viral load and parasitoid–pathogen (without complete elimination) and never provided permissible window for the quantification of the systemic cost. Periodic multiple chemotherapy treatment maximizes uninfected T–lymphocytes cells and macrophages cells concentration, control the amount of frequent drugs administration, thereby reducing the consequences of drug severities and minimizes systemic cost. Continuous multiple chemotherapy treatment with optimal control measures maximizes and sustained healthy T–lymphocytes cells and macrophages cells, eliminate completely both viral load and parasitoid–pathogen virions at the earliest time interval for a cohesive administration of chemotherapy treatment. This later approach also provided permissible window for the evaluation of benefit on treatment cost and thus established the fact that minimization of systemic cost is a function of defined optimal control measures and optimal weight factors on treatment factors.

Finally, investigation clearly indicated that the overall maximization of both healthy T–lymphocytes and macrophages cells are independent of prolong chemotherapy administration but on a large scale, depends on the toxicity of drugs initiated at set–point. Therefore, this model, which strongly established elimination tendency of dual HIV–pathogen infections is viewed as an ideal intellectual source, which that could be implemented on related infectious diseases.

My utmost appreciation to my formal indispensible academic supervisor, Prof. Lebedev, K. A., Kuban State University, Krasnodar, for his wonderful backing during the period of my Ph.D. program. Also, I would like to thank the anonymous referee(s) for his/her valuable comments on the first version of the manuscript, which have led to an improvement in this revised version.

I declare that this manuscript does not possess plagiarized contents and is devoid of any conflict of interest. The author hereof is the sole sponsor of this research work

http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.400.9056
Bassey EB, Lebedev KA. On Analysis of Parameter Estimation Model for the Treatment of Pathogen–Induced HIV Infectivity. Open Access Library Journal. 2016;3(4):1–13.
Agur Z. (1989) A new method for reducing cytotoxicity and the anti–AIDS drug AZT. In: Levine DS, et al. (Eds.), Biomedical Modeling and Simulation, Scientific Publishing Services, India, p. 59–61,
Bajaria SH, Webb G, Kirschner DE. Predicting differential responses to structured treatment interruptions during HAART. Bull Math Biol. 2004;66(5):1093–1118.
Bonhoeffer S, Rembiszewski M, Ortiz GM, et al. Risks and benefits of structured antiretroviral drug therapy interruptions in HIV–1 infection. AIDS. 2000;14(15):2313–2322.
Brandt ME, Chen B. Feedback control of a biodynamical model of HIV–1. IEEE Trans Biomed Eng. 2001;48(7):754–759.
Butler S, Kirschner D, Lenhart S (1997) Optimal control of the chemotherapy affecting the infectivity of HIV. Arino O, et al. (Eds.), Advances in Mathematical Population Dynamics– Molecules, Cells and Man, pp. 557–569.
Callaway DS, Perelson AS. HIV–1 infection and low steady state viral loads. Bull Math Biol. 2001;64(1):29–64.
Fister KR, Lenhart S, McNally JS. Optimizing chemotherapy in an HIV Model. Electr J Diff Eq. 1998;32: 1–12.
http://dx.doi.org/10.1007/978–1–4612–6380–7
Bassey BE, Andreyevich LK. On Quantitative Approach to Parametric Identifiability of Dual HIV–Parasitoid Infectivity Model. Open Access Library Journal. 2016;3(8):1–14.
Zarei H, Kamyad AV, Effati S. Maximizing of Asymptomatic Stage of Fast Progressive HIV Infected Patient Using Embedding Method. Intelligent Control and Automation. 2010;1(1):48–58.
Joshi HR. Optimal Control of an HIV Immunology Model. Optimal Control Applications and Methods. 2002;23(4):199–213.
Kirschner ED, Webb FG. Immunotherapy of HIV–1 infection. Journal of Biological Systems. 1998;6(1):71–83.
Kirschner D, Webb GF. A Model for Treatment Strategy in the Chemotherapy of AIDS. Bull Math Biol. 1996;58(2):367–390.
Bajpai P, Chaturvedi A, Dwivedi AP. Optimal Therapeutic Control Modeling for Immune System Response. International Journal of Computer Applications. 2011;21(4):0975–8887.
Bassey EB, Kimbir RA, Lebedev KA. On Optimal Control Model for the Treatment of Dual HIV–Parasitoid Pathogen Infection. J Bioengineer & Biomedical Sci. 2016;7: 212.
Ho DD, Neumann AU, Perelson AS, et al. Rapid Turnover of Plasma Virions and CD4 Lymphocytes in HIV–1 Infection. Nature. 1995;273(6510):123–126.
Kirschner D, Lenhart S, Serbin S. Optimal control of the chemotherapy of HIV. Journal of Mathematical Biology. 1997;35(7):775–792.
Kamien MI, Schwartz NL (1991) Dynamic Optimization. (2nd edn), North–Holland, USA, p. 1–43.
Adams BM, Banks HT, Davidian M, et al. HIV Dynamics: Modeling, data analysis, and optimal treatment protocols. J Comp Appl Math. 2005;184(1):10–49.
Lisziewicz J, Rosenberg E, Liebermann J. Control of HIV despite the discontinuation of anti–retroviral therapy. N Engl J Med. 1999;340(21):1683–1684.
Bassey EB. Optimal control model for immune effectors response and multiple chemotherapy treatment (MCT) of dual delayed HIV – pathogen infections. SDRP Journal of Infectious Diseases Treatment & Therapy. 2017;1(1):1–18.
Wiah EN, Otoo H, Nabubie IB, et al. Nonlinear dynamics and chaos in HIV/AIDS epidemic model with treatment. Applied Mathematics. 2014;4(3):86–96.
Zhu H, Zou X. Dynamics of a HIV–1 infection model with cell–mediated immune response and intracellular delay. Discrete and continuous dynamical systems series B 2009;12(2):511–524.
Rico–Ramirez V, Napoles–Rivera F, González–Alatorre G, et al. Stochastic optimal control for the treatment of a pathogenic disease. Computer Aided Chemical Engineering. 2010;28(C):217–222.
Hattaf K, Yousfi N. Two optimal treatments of HIV infection model. World Journal of Modelling and Simulation. 2012;8(1):27–35.
Bassey E. On Optimal Control Pair Treatment: Clinical Management of Viremia Levels in Pathogenic–Induced HIV–1 Infections. Biomed J Sci & Tech Res. 2017;1(2):1–9.
Bassey E. On Discretization Method for Optimization Control Model for the Treatment of Pathogenic Induced HIV Infection. Curr Trends Clin Med Imaging. 2017;1(5):1–6.
Lukes DL (1982) Differential Equations: Classical to Controlled. (1st edn), Mathematics in Science and Engineering, Academic Press, New York, USA, 162: 321.
Pontryagin LS, Boltyanskii VG, Gamkrelidze RV, et al. The Mathematical Theory of Optimal Processes. Gordon & Breach Science Publishers, New York, USA, 1986;4:360.

Submit manuscript...

Journal of

eISSN: 2473-0831

Analytical & Pharmaceutical Research

Dynamic Optimal Control Model for Periodic Multiple Chemotherapy (PMC) Treatment of Dual HIV-Pathogen Infections

Bassey E Bassey

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Abstract

Abbreviations

Introduction

Material and methods

Optimality Control for PMC Treatment

Discussion

Conclusion

Acknowledgments

Conflicts of interest

References

Citations

Journal Menu

Useful Links