The first study concerned with the determination of ezetimibe EZE in presence of its alkaline degradation product were developed and validated using different chemometric techniques [bivariate, classical least square (CLS), and principle component regression (PCR), partial least square (PLS)], with kinetic study and calculation of half-life time and activation energy which essential for quality control of its product. Application of the suggested techniques were successfully applied in synthetic mixture and in pharmaceutical preparations, the results obtained by the proposed techniques were statistically comparable with those obtained by the reported method. All the proposed techniques were validated according to international conference on harmonization (ICH) guidelines.

Keywords: Ezetimibe; Kinetic study; Bivariate, Classical least square; Principle component regression; Partial least square

CLS, classical least square; PCR, principle component regression; PLS, partial least square; ICH, International conference on harmonization; EZE, ezetimibe

Ezetimibe (EZE), a selective inhibitor of intestinal cholesterol and related phytosterol absorption, is designated as1-(4-fluorophenyl)-3(R)-[3-(4-fluorophenyl)-3(S)-hydroxypropyl]-4(S)-(4-hydroxyphenyl) -2-azetidinone Figure 1, It blocks the intestinal absorption of dietary and biliary cholesterol, without affecting the uptake of triglycerides or fat soluble vitamins, this reduce the overall delivery of cholesterol to the liver, thereby promoting the synthesis of LDL receptors and a subsequent reduction in serum LDL-C.^1–7 The literature is enriched with several techniques for determination of (EZE) in pharmaceutical dosage forms and/or biological fluids, including HPLC methods for the determination of ezetimibe are reported,^8–32 TLC,^{15,18,32–37} LC,^38–45 chemometry,^32,46 Spectrophotometric methods,^{13,30,31,47–68} UPLC,^69,70 densitometry,^54,71 electrokinetic chromatography,⁷² electrophoresis,⁷³ voltammetry,⁷⁴ spectrofluorometry,⁷⁵ other related with degradation and elucidation of alkaline degradate of ezetimibe.^76–78

Figure 1 Chemical structure of Ezetimibe.

The aim of this work is to develop a simple, economic, rapid, sensitive, accurate and validated stability indicating methods for determination of (EZE) in presence of its alkaline degradate without sophisticated instruments or any pretreatment steps for the quality control of EZE in pharmaceutical preparations.

Theory of bivariate method⁷⁹

The principle of bivariate calibration is the measurement of two components (A and B) at two selected wavelengths (λ1 and λ2) to obtain two equations:

A_AB1 = m_A1C_A + m_B1C_B + e_AB1 (1)

A_AB2 = m_A2C_A + m_B2C_B + e_AB2 (2)

The resolution of such equations set allows the evaluation of CA and CB values:

C_A = (A_AB1 - e_AB1- m_B1C_B) / m_A1 (3)

C_B = [m_A2 (A_AB1 - e_AB1) + m_A1 (e_AB2 - A_AB2)] / m_A2m_B1 - m_A1m_B2 (4)

Where:

1. C_A, C_B is the concentration of component A, component B.
2. m_A1, m_A2 are the slope values of component A at λ₁, λ₂.
3. m_B1, m_B2 are the slope values of component B at λ₁, λ₂.
4. A_AB1, A_AB2 are the absorbance values of the binary mixture at λ₁, λ₂.
5. e_AB1, e_AB2 are the sum of the intercepts of components A, B at λ₁, λ₂.

1. This simple mathematic algorithm allows the resolution of the two components by measuring the absorbance of their mixture at the two selected wavelengths and using the parameters of the linear regression functions evaluated individually for each component at the same wavelengths.

According to Kaiser method, the slope values of the linear regression equations for both components at different wavelengths were used to calculate the sensitivity matrices (M) to find out the optimum pair of wavelengths (highest matrix value) at which the binary mixture was determined.

Instruments

1. A double beam UV-Visible spectrophotometer (Shimadzu 1800, Japan) and it is connected to IBM compatible computer. The software UV-Probe Ver. 2.43.
2. Hot plate (Torrey Pines Scientific, USA).
3. Rota-Vapor SCI-Logics (RE-100-PRO) with Buchi pump.
4. Precoated TLC plates, silica gel 60 GF₂₅₄, (20 × 20), 0.22 mm thickness (Fluka, Chemie, Switzerland).

Materials

Pure standard: Ezetimibe was kindly provided by E.I.P.I.Co Company, Cairo, Egypt, with purity of 99.9%.

Pharmaceutical dosage form: Zetamibe® tablet: manufactured by Adwia; labeled to contain 10 mg of ezetimibe per tablet, (Batch No. 133822).

Zetajon® tablet: Manufactured by MUP (medical union pharmaceuticals); labeled to contain 10 mg of ezetimibe per tablet, (Batch No. 1501189).

Chemical and reagent:

1. Methanol (HPLC grade) obtained by Sigma-Aldrich company, Germany.
2. 0.1 M methanolic sodium hydroxide solution.
3. Whatman filter paper no41.
4. Ethyl acetate and n-hexane.
5. Hydrochloric acid.

Standard solution

Stock solution of 1mg/mL for (EZE) was prepared by dissolving 100 mg of (EZE) in 100 ml pure. Different sets of working solution at various concentrations were prepared by appropriate dilution of the stock solution.

Kinetic study

Two sets of working standard solutions of ezetimibe (4.88 x 10^-4 and 1.47 x 10^-4mol/L) were prepared by dissolving in 10ml methanol into 100-ml volumetric flask and diluting to the mark with 0.1M NaOH.

Alkaline degradation of EZE⁷⁷

100mg of EZE was dissolved in 50mL (0.1M methanolic sodium hydroxide); the solution was refluxed at 80ºC for 30minutes. The time required for complete degradation was followed by spotting on TLC plates at 10minutes intervals for 30minutes. The plates was developed using ethyl acetate: n-hexane (2:1, v/v), which indicate complete degradation with clear separation. After completion, the solution was cooled to room temperature then neutralize with 1M hydrochloric acid. The neutralized solution was filtered. Then evaporate the solution under vacuum till dryness, the residue was dissolved by pure methanol and filtered (several times), evaporate the filtrate using Rota-vapor under vacuum, the residue was dissolved in 100 ml methanol to give degradate stock solution of (1mg/mL).

Procedures

Construction of calibration curve for bivariate

Different aliquots equivalent to (20-200µg) of both ezetimibe and its degradate were accurately transferred from their standard solutions (100 µg/ ml) into two separate series of 10 ml volumetric flasks and completed to volume with methanol. The absorption spectra (from 200 to 400nm) of these solutions were recorded using methanol as a blank. The regressions equations at 232 and 247nm for ezetimibe and its alkaline degradate were computed.

Experimental design of chemometric models⁸⁰

Zissis et al.⁸¹ constructed multilevel multifactor experimental design was applied for the construction of the calibration and validation sets. Five-levels, two factors experimental design was used in which 0.8, 0.9, 1, 1.1 or 1.2ml aliquots of both intact and degraded form of ezetimibe standard solutions were combined and diluted to 10-ml volumetric flask with methanol. The concentrations details are given in Table 1. The absorption spectra of the prepared mixtures were recorded over the wavelength range 205-300 nm with 1nm interval thus the produced spectral data matrix has 25 rows representing different samples and 96 columns representing wavelengths (25 x 96). For construction of the models, to build the CLS and PCR models, feed the computer with the absorbance and concentration matrices for the training set, use the training set absorbance and concentration matrices using MATLAB version R2013b (8.2.0.701), with PLS-Toolbox 2.1.Software for the calculations. The concentrations were calculated from the corresponding regression equations.

Kinetic study

Effect of time on the reaction: Two sets of standard solution of ezetimibe (4.88x10^-4 and 1.47x10^-4mol/L) were prepared in 0.1M methanolic NaOH and refluxed as rapidly as possible at 80ºC and 0.1ml from the refluxed solutions was quantitatively transferred into 10ml volumetric flask for 30minutes at 10minutes interval. The flasks were completed to volume with methanol and measured by applying in the previously described bivariate method for the determination of the remaining intact ezetimibe from its corresponding regression equation.

Effect of sodium hydroxide concentration on the reaction: The mentioned procedure was followed using 0.05 and 0.1M methanolic NaOH in the degradation of 4.88 x 10^-4mol/L of ezetimibe.

Effect of temperature on the reaction: The mentioned procedure was followed using series of volumetric flask containing standard solution of ezetimibe (4.88 x 10^-4 mol/L), were prepared in 0.1M methanolic NaOH and refluxed as rapidly as possible and refluxed at different temperature till 80ºC with 10ºC interval for 30 minutes and then 0.1 ml from the refluxed solutions was quantitatively transferred into 10ml volumetric flask. The flasks were completed to volume with methanol and measured by applying in the previously described bivariate method for the determination of the remaining intact ezetimibe from its corresponding regression equation.⁸²

Activation energy

The same procedure under 7.3.3. Effect of temperature on the reaction was repeated using concentration of EZE (1.47 x 10^-4mol/L) only and two different temperatures (30º and 80ºC).

Specificity (Laboratory prepared mixture)

The procedure related to bivariate method was applied using aliquots of ezetimibe solution (100μg/ml) containing (180-40µg) and aliquots of its alkaline degradation product solution (100μg/ml) of (20-160µg). Ezetimibe concentrations were calculated using equation (3).

Application of pharmaceutical formulation

Ten tablets of each of zetamibe® tablet and Zetajon® tablet were accurately weighed, crushed and mixed well. An amount equivalent to 10 mg of ezetimibe was weighed and transferred into two separate 100ml volumetric flask. To ensure complete extraction of drug, it was sonicated for 15minutes in 10ml of methanol and filtered into 100ml volumetric flask, then complete to the volume with methanol to obtain a solution labeled to contain 100μg/ml of ezetimibe.

An ideal stability indicating method is that quantifies the pure drug alone and also resolves its degradation product. It was found that the complete degradation of ezetimibe proceeds optimally in alkaline media and at elevated temperature, and then severe overlapping between ezetimibe and its alkaline degradation product Figure 2 can be resolved by using analytical techniques of great utility for extracting both qualitative and quantitative determination using zero-order absorption spectra.

Figure 2 Zero order absorption spectra of 20 µg/mLof EZE and its alkaline degradate.

The structure of the alkaline degradate was elucidated and confirmed by using 1H NMR technique where, The 1H NMR of intact ezetimibe Figure 3, showed a characteristic proton of aliphatic (OH) at 4.86ppm, aromatic (OH) at 9.40ppm and aliphatic proton (CH2) at 1.75 ppm. While, 1H NMR of degradate Figure 4, showed disappearance of aliphatic (OH) at 4.86ppm and appearance of characteristic proton of (CO-NH) at 9.98ppm and aromatic OH still present at 9.06ppm.

Figure 3 1H NMR of intact ezetimibe in DMSO.

Figure 4 1H NMR of alkaline degradation product of ezetimibe in DMSO.

So, we can conclude that ezetimibe undergo recyclization⁷⁷ under the alkaline condition with elevated temperature as shown below.

Optimization of the experimental condition

Bivariate method: In order to apply the bivariate method in the resolution and determination of ezetimibe from its alkaline degradate in their binary mixture. This method is based on a simple mathematic algorithm, in which the data used derives from seven linear regression calibration equations at different selected wavelengths in the region of overlapping; 222, 227, 232, 237, 242, 247 and 252nm. The calibration graph equations and their respective linear regression coefficients were obtained directly with the aim of ensuring that; there was a linear relationship between the absorbance and the corresponding concentration, so the rate of the reaction was found to be dependent on the drug concentration. All of the calibration graphs at the selected wavelengths showed a satisfactory linear regression coefficient (r2 ≥ 0.9998).

According to Kaiser Method,⁸³ the slope values of the linear regression equations for both drugs at the selected wavelengths were used to calculate the sensitivity matrices (K) to find out the optimum pair of wavelengths which assured the best sensitivity for the quantitative determination of EZE. It was found that; the slopes at 232 and 247 nm gave the maximum value of (K) as shown in Table 2 and thus the two selected wavelengths had been chosen for the analysis.

The linear regression equations for the graphs at 232 and 247 nm were found to be:

1. For ezetimibe

Y₂₃₂ = 0.0526 x - 0.0037 (r² = 0.9999).

Y₂₄₇ = 0.0429 x - 0.0034 (r² = 0.9999).

1. For alkaline degradate

Y₂₃₂ = 0.0155 x - 0.0002 (r² = 0.9999).

Y₂₄₇ = 0.0233 x + 0.0003 (r² = 0.9998).

Where, y is the absorbance, x is the drug concentration in µg/ml and r² is the squared correlation coefficient.

Linearity ranges, regression equations, intercepts, slopes and squared correlation coefficients for the calibration data were presented in Table 3. The results of accuracy, repeatability and intermediate precision of the method were presented in Table 4.

The analysis of laboratory prepared mixture of EZE and its alkaline degradate in different ratio was applied and presented in Table 5, EZE could be determined in presence of up to 80% of degradate with mean percentage recovery 99.95 ± 0.699.

The validity of the method was assessed by adopting standard addition technique, which illustrate accurate results without any interference from the excipient as presented in Table 6 & Table 7.

Kinetic investigation: Bivariate method was used to determine the order of the alkaline degradation rate, the rate of the reaction was found to be dependent on the drug concentration which means that the rate increases as the studied drugs concentration increases, indicating that the reaction rates obeys the following equation:

Rate = k’ [drug]ⁿ and then,

log (rate) = log k’ + n log [drug].

Where, k’ is the constant rate and n is the order of the reaction.

The extent of complete degradation depends on the alkalinity, temperature and time; therefore the effects of these variables were studied. Two different concentrations of ezetimibe (4.88 x 10^-4 and 1.47 x 10^-4 mol/L) were used for the study of the effect of time by following the decrease in the concentration of EZE within 30minutes at10minutes interval with constant temperature at 80ºC, Figure 5 is plot of log of the remaining concentrations versus time.

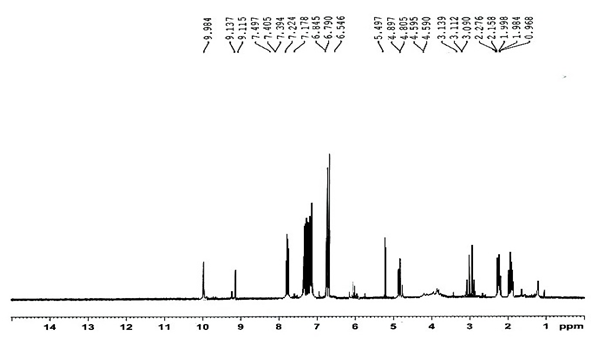
Figure 5 Kinetic plots of the alkaline degradation for 4.88x10-4mol/L and 1.47x10-4mol/L of ezetimibe using 0.1M NaOH.

These obtained curves show that the obtained slope (S) was nearly the same and the linear relationship obtained indicates that the reaction follows first order kinetic and related to bimolecular reaction since the water considered as a reactant but present in large excess, so the change in concentration is negligible. Such reaction is considered to follow pseudo-first order kinetic with applying all equations which describing first order kinetic reaction.

The rate of the degradation (k) was calculated from the equation S = -k/2.303 and t_1/2 was calculated from the equation t_1/2= ln2 / k = 0.693 [84], and the results are presented in Table 8.

The study of the effect of NaOH concentration on the reaction rate Figure 6 shows that the reaction rate was increased by rising sodium hydroxide concentration.

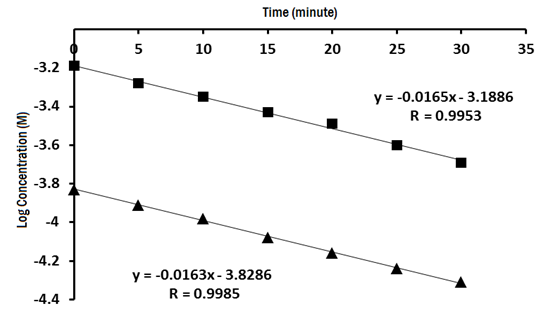
Figure 6 plot for the effect of sodium hydroxide concentration on the reaction rate of degradation of 4.88 x 10-4mol/L.

Calculation of activation energy⁸⁵: Figure 7 shows that temperature was essential for complete degradation. So calculation of activation energy (Ea) is very important to determine the minimum energy required for initiating the reaction. The data obtained from the Figure 7 which presented in Table 9, could be used to calculate Eaby substituting in the following equation:

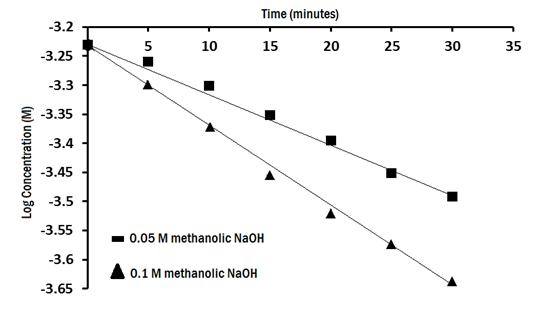
Figure 7 Plot for the effect of temperature (30º C and 80º C) on the reaction rate of degradation of (1.47x10-4mol/L) of ezetimibe.

Log k₁/k₂ = Ea/ (2.303 R) x [(T₂-T₁) / (T₁T₂)] (6)

This equation was derived from Arrhenius equation k = Ae-Ea/RT

Where, k is rate of the reaction, A is pre-exponential, e^-Ea/T is Boltzmann’s factor, Ea is activation energy, T is temperature in kelvin and R is universal gas constant.

Chemometric models (CLS, PCR, PLS): Various criteria have been developed to select the optimum number for calibration and validation sets. Thirteen samples (odd numbers of samples) were chosen and used for calibration set and twelve (even numbers of samples) were used for external validation.

For the CLS method, the training set was used for constructing CLS model or (K) matrix (i.e. absorptivity at different wavelengths) but poor predictions were obtained. The results were greatly improved by using the CLS model with nonzero intercept.

The predicted concentrations were compared with the known concentrations of the compounds in each calibration sample. The root mean squares error of cross-validation (RMSECV) was calculated for each method for examining the errors in the predicted concentrations. The optimum number of factors was selected by following the criterion of Haal and and Thomas.⁸⁶ The selected model was that with the smallest number of factors such that RMSECV for that model was not significantly greater than RMSECV from the model with additional factor. A number of factors were found to be optimum for the mixture of ezetimibe and the degradation product using PCR and PLS as shown in Figure 8 & Figure 9.

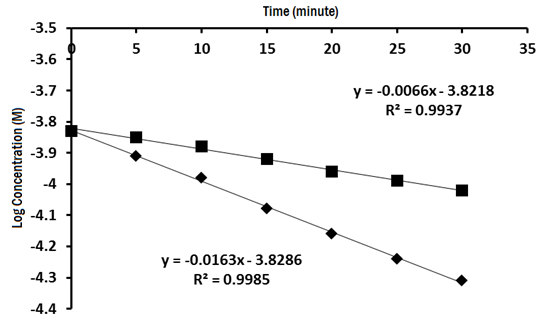
Figure 8 RMSECV plot of the cross validation results of the calibration set as a function of the number of latent variables (LVs) used to construct the PCR model.

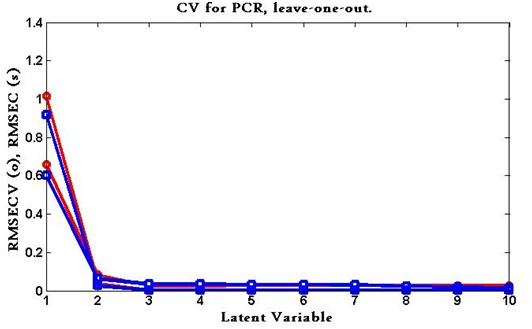
Figure 9 RMSECV plot of the cross validation results of the calibration set as a function of the number of latent variables (LVs) used to construct the PLS model.

Recoveries, mean, standard deviation, RMSEC, RMSEP and other validation parameters for ezetimibe in both models were shown in Table 10 & Table 11.

Table 12 & Table 13 show statistical comparison of the results obtained by the proposed methods and the reported spectrophotometric method.⁸⁷ There is no significant difference between the proposed methods and the reported method related to accuracy and precision as the calculated t and F values are less than the theoretical ones and the comparison related to one way ANOVA which applied for each zetamibe® and zetajon® tablets.

It’s the first time to develop spectrophotometric methods concerned with determination of ezetimibe in presence of its alkaline degradation product. The previous work deals with degradation ezetimibe and confirmation of the structure of degradate only.⁷⁷

The present work involves stability indicating spectrophotometric methods (bivariate and chemometric models) which applied for the resolution of overlapping bands. Kinetic studies of the decomposition of EZE are essential for the quality control of its product and to determine the order of the reaction, so the kinetic study of alkaline degradation of EZE was applied.

It’s the very important to know both activation energy (Ea) and half-life(t_1/2) to determine the minimum energy required for initiating the reaction and the time required for 50% of the reaction to be occurred. It’s too simple to calculate both Ea and t_1/2 after determination of the order of the reaction.

We can conclude that the developed methods have the advantages of being simple and not expensive methods. The procedures applied in each method do not need any sophisticated instruments, critical reactions or any pretreatment step. The proposed methods are found to be sensitive, selective and accurate with no significant difference of the precision compared with the spectrophotometric reported method.⁸⁷

They could be applied for routine analysis of ezetimibe in pure form or in its pharmaceutical formulation without interference from the excipients or the degradation product and could also be easily used in quality control laboratory for its analysis. The methods are also suitable and valid for application in laboratories lacking liquid chromatographic instruments.

The advantage of bivariate method over the other chemometric techniques, there is no need for full spectrum data and no data processing is required.

I am deeply thankful to ALLAH, by the grace of whom this work was realized. I wish to express my indebtedness and gratitude to staff members of Analytical Chemistry Department for their valuable supervision, continuous guidance, and encouragement throughout the whole work.

The authors declare there is no conflict of interests.

None.

1. Leitersdorf E. Selective cholesterol absorption inhibition:a novel strategy in lipid–lowering management. Int J Clin Pract. 2002;56(2):116–119.
2. Heek MV, Farley C, Compton D, et al. Ezetimibe selectively inhibits intestinal cholesterol absorption in rodents in the presence and absence of exocrine pancreatic function. Br J pharmacol. 2001;134(2):409–417.
3. Carvalho EM, Periera FA, Junker J. how well does NMR behave in natural products structure determination? A survey of natural products published in 2007 and 2008. INIS 2009;40(43).
4. Heek MV, Farley C, Compton D, et al. Comparison of the activity and disposition of the novel cholesterol absorption inhibitor, SCH58235, and its glucuronide, SCH60663. Br J Pharmacol. 2000;129(8):1748–1754.
5. Altman SW, Davis HR, Zhu LJ, et al. Niemann–pick C1 like 1 proton is critical for intestinal cholesterol absorption. Science. 2004;303(5):1201–1204.
6. Budawari S. The Merk index. 13th edn. Whitehouse Station, New Jersey, USA, 2001. 148 p.
7. Darkes MJ, Poole RM, Goa KL. Ezetimibe. American Journal of Cardiovascular Drugs. 2003;3(1):67–76.
8. Gajjar KKA, Shah VD. Development and validation of a stability–indicating reversed–phase HPLC method for simultaneous estimation of rosuvastatin and ezetimibe from their combination dosage forms. Eurasian Journal of Analytical Chemistry. 2010;5(3):265–283.
9. Sonawane SS, Shirkhedkar AA, Fursule RA, et al. Application of UV–spectrophotometry and RP–HPLC for simultaneous determination of atorvastatin calcium and ezetimibe in pharmaceutical dosage form. Eurasian Journal of Analytical Chemistry. 2006;1(3):31–41.
10. Patel V, Baldha R, Patel D. Sugar–Decorated Dendritic Nanocarriers:Encapsulation and Release of the Octahedral Rhenium Cluster Complex [Re6S8(OH)6]4−. Asian Journal of Chemistry. 2010;5(12):2507–2511.
11. Sama JR, Kalakuntla RR, Rao VSN, et al. Stability indicating RP–HPLC analytical method development and validation for simultaneous estimation of atorvastatin and ezetimibe in bulk as well in pharmaceutical dosages form by using PDA detector. Der Pharmacia Lettre. 2010;2(1):427–436.
12. Bhatt KK, Shankar MB. Evaluation of antioxidant and hypolipidemic activity of vedic guard, a polyherbal formulation. International Journal of Pharmaceutical Scvience & Research. 2010;1(10):114–127.
13. Chaudhari BG, Patel MN, Shah PB, et al. Stability–Indicating Reversed–Phase Liquid Chromatographic Method for Simultaneous Determination of Atorvastatin and Ezetimibe from Their Combination Drug Products. J AOAC Int. 2007;90(6):1539–1546.
14. Chaudhari BG, Patel MN, Shah PB. Stability–indicating reversed–phase liquid chromatographic method for simultaneous determination of simvastatin and ezetimibe from their combination drug products. J AOAC Int. 2007;90(5):1242–1249.
15. Seshachalam U, Kothapally CB. HPLC Analysis for Simultaneous Determination of Atorvastatin and Ezetimibe in Pharmaceutical Formulations. Journal of Liquid Chromatography & Related Technologies. 2008;31(5):714–721.
16. Kumar D, Sujan D, Viajayasree V, et al. J Chem. 2009;6:541–544.
17. Astaq M, Khana I, Qutab S, et al. J Chil Chem Soc. 2007;52:1220–1223.
18. El–moghazy SM, El–Azem MA, Mohamed MF, et al. development and validation of HPLC, TLC and derivative spectrophotometric methods for the analysis of ezetimibe in the presence of alkaline induced degradation products. Journal of Chinese Chemical Socirty. 2009;56(2):360–367.
19. Sistla R, Tata VS, Kashyap YV, et al. Development and validation of a reversed–phase HPLC method for the determination of ezetimibe in pharmaceutical dosage forms. J Pharmaceut Biomed Anal. 2005;39(2–3):517–522.
20. Akmar SK, Lata K, Thomas A, et al. Reverse phase high performance liquid chromatography method for estimation of ezetimibe in bulk and pharmaceutical formulations. Indian Journal Pharmaceutical Science. 2007;69(5):695–697.
21. Singh S, Singh B, Bahuguna R, et al. Stress degradation studies on ezetimibe and development of a validated stability–indicating HPLC assay. J Pharmaceut Biomed Anal. 2006;41(3):1037–1040.
22. Basha SJ, Naveed SA, Tiwari NK, et al. Concurrent determination of ezetimibe and its phase–I and II metabolites by HPLC with UV detection:quantitative application to various in vitro metabolic stability studies and for qualitative estimation in bile. J Chromatogr B Analyt Technol Biomed Life Sci. 2007;853(1–2):88–96.
23. Sahu S, Narajan UL, Garnaik B, et al. Inter J Res Pharmaceut Biomed Sci. 2013;4:1249–1255.
24. Kumar P, Ahmad Y, Ghosh A. Der Pharma. Chemica. 2012;4:1296–1304.
25. Latha DM, Ammani K, Kumar PJ, et al. Int J Res Pharmac Chem. 2014;4:406–414.
26. Reddy NN, Rao JV. Int J Pharmaceut Res Biomed Anal. 2012;1:32–41.
27. Kumar P, Ghosh A, Chaudhary M. Stability indicating method development for simultaneous estimation of ezetimibe and atorvastatin in pharmaceutical formulations by RP–HPLC. Pharmaceutica Analytica Acta. 2012;3(6):164–170.
28. Varma PSRchNP, Rao AL, Dinda SC. Development and validation of stability indicating RP–HPLC method for simultaneous estimation of rosuvastatin and ezetimibe in combined tablet dosage form. Rasayan J Chem. 2012;5(3):269–279.
29. Hefnawy M, Omar MA, Julkhuf S. J Pharm Biomed Anal. 2009;50:527–534.
30. Chetan MB, Jane J, Subrahmanyam EVS. Int J Res Pharmaceut Biomed Sci. 2011;2:241–244.
31. Tollesten L. For drug impurity identification. Elsevier Science; 2000:266–297.
32. Lotfy HM, Aboulalamein AM, Hegazy MA. JAOAC Inter. 2010;39:1844–1855.
33. Dixit PR, Barhate RC, Nagarsenker SM. J Chromatographia. 2008;67(1–2):101–107.
34. Shrestha B, Stephenrathinaraj B, Patel S, et al. J Chem. 2010;7:1206–1211.
35. Aiyalu R, Mani K. HPTLC method development, validation, and stress degradation studies for atorvastatin and ezetimibe in multicomponent tablet dosage form. Medicinal Chemistry Research. 2012;21(7):1297–1301.
36. Chaudhari BG, Patel NM, Shah B. Development and validation of a HPTLC method for the simultaneous estimation of atorvastatin calcium and ezetimibe. Indian Journal of Pharmaceutical Science. 2006;68(6):793–796.
37. Mahadik MV, Dhaneshwar SR. Asian J Pharm Sci. 2007;2:182–190.
38. Doshi S, Kachhadia PK, Joshi HS. Validation of a stability indicating lc method for assay of ezetimibe in tablets and for determination of content uniformity. Chromatographia. 2008;67(1):137–142.
39. Oswald S, Scheuch E, Cascorbi I, et al. A LC–MS/MS method to quantify the novel cholesterol lowering drug ezetimibe in human serum, urine and feces in healthy subjects genotyped for SLCO1B1. J Chromatogr B Analyt Technol Biomed Life Sci. 2006;830(1):143–150.
40. Li S, Liu G, Jia J, et al. Liquid chromatography negative ion electrospray tandem mass spectrometry method for the quantification of ezetimibe in human plasma. J Pharmaceut Biomed Anal. 2006;40(4):987–992.
41. Oliveira PR, Junior LB, Fronza M, et al. Chromatographia. 2006;63:315–320.
42. Bahrami G, Mohammadi B, Khatabi PM, et al, Application of one step liquid chromatography electrospray tandem MS/MS and collision–induced dissociation to quantification of ezetimibe and identification of its glucuronated metabolite in human serum: A pharmacokinetic study. J Chromatogr B Analyt Technol Biomed Life Sci. 2010;878(28):2789–2795.
43. Ramana B, Sharmaa BA, Butalab R, et al. Structural elucidation of a process related impurity in ezetimibe by LC/MS/MS and NMR. J Pharm Biomed Anal. 2010;52(1):73–78.
44. Qutab SS, Razzaq SN, Khan IU, et al. J Food Drug Anal. 2007;15:139–144.
45. Ozaltin N, Ucakturk E. Chromatographia. 2007;66:587–591.
46. Palabiyit L, Onur F, yardimci C, et al. Quimica Nova. 2008;31:1121–1124.
47. Lakshmi PBS, Ramchandran D, Rambabu C. E J Chem. 2010;7:101–104.
48. Sharma M, Mhaske DV, Mahadik M, et al. UV and three derivative spectrophotometric methods for determination of ezetimibe in tablet formulation. Indian J Pharm Sci. 2008;70(2):258–260.
49. Jain N, Jain R, Swami H, et al. Spectrophotometric method for simultaneous estimation of simvastatin and ezetimibe in bulk drug and its combined dosage form. Indian Journal of Pharmacy and Pharmaceutical Science. 2009;1(1):170–175.
50. Rajput S, Raj H. Simultaneous spectroscopic estimation of ezetimibe and simvastatin in tablet dosage forms. Indian Journal of Pharmaceutical Science. 2007;69(6):759–762.
51. Lotfy HM. Determination of Simvastatin and Ezatimibe in Combined Tablet Dosage Forms by Constant Center Spectrophotometric Method. Int J Pharm Pharm Sci. 2012;4(4):673–679.
52. Lotfy HM, Hegazy MA. Spectrochim Acta Part A. 2013;113:107–114.
53. Lotfy HM. Int J Pharm Pharm Sci. 2014;6:735–741.
54. Baghdady YZ, AlGhobashy MA, Abdel Aleem AA, et al. Spectrophotometric and TLC densitometric methods for the simultaneous determination of Ezetimibe and Atorvastatin calcium. J Adv Res. 2013;4(1):51–59.
55. Belal TS, Daabees HG, Khalek AMM, et al. J Pharm Anal. 2013.
56. Deshmukh DD, Bhatia NM, More NH, et al. Asian J Chem. 2008;20:155–160.
57. Savithri R, Bindu NSS, Bhargavi PS, et al. Dual Wavelength UV – Spectrophotometric method for simultaneous estimation of atorvastatin and ezetimibe in bulk and their combined tablet dosage form. Der Pharmacia Sinica. 2011;2(5):251–258.
58. Gajjar KA, Shah VD. Int J PharmTech Res. 2010;2:404–410.
59. Kumar YP, Sridhar C, Reddy AS, et al. Development and validation of spectrophotometeric method for estimation of ezetimibe in tablet formulation. Journal of global Trends in Pharmaceutical Science. 2011;2:118–130.
60. Farouk M, Aziz AO, Nagi R, et al. Validated chromatographic methods for determination of some anti–hyperlipidemic used drugs. J Biomed Sci and Res. 2010;2:202–211.
61. Moussa BA, Mohamed NF, Youssef NF. Derivative spectrophotometric method for simultaneous determination of ezetimibe and simvastatin in combined tablets. Eur J Chem. 2010;1(4):348–351.
62. Imran M, Singh RS, Pharmazie CS. 2006;61:766–769.
63. Ramachandran S, Mandal BK, Navalgund SG. Stability–indicating HPLC method for the simultaneous determination of valsartan and ezetimibe in pharmaceuticals. Tropical Journal of Pharmaceutical Research. 2014;13(5):809–817.
64. Lakishmi PBS, Ramchandran D, Rambabu C. E–journal Chem. 2010;7:101–104.
65. Sekaran CB, Tirupatamma PL, Rajitha V, et al. B Int J Pharm Sci. 2012;4:396–401.
66. Mishra P, Gupta A, Shah JK. Indian Chem Soc. 2007;84:945–947.
67. Shravya, Chandan RS, Gurupadayya BM, et al. Int J Pharmac Techno. 2010;2:1046–1056.
68. Shravya, Chandan RS, Gurupadayya BM, Sireesha M. Int J Res Ayur Pharm. 2011;2:521–525.
69. Goel A, Baboota S, Sahni JK, et al. Development and validation of stability–indicating assay method by UPLC for a fixed dose combination of atorvastatin and ezetimibe. J Chromatogr Sci. 2012;51(3):222–228.
70. Devu S, Gupta A, Srinivas KS, et al. J Chromat Separation Techniq. 2012;3:131–137.
71. Dhaneshwar SS, Dhaneshwar SR, Deshpande P, et al. Acta Chromatogr. 2007;19:141–147.
72. Dalmora SL, Oliveira PR, Barth T, et al. Development and Validation of a Stability–indicating Micellar Electrokinetic Chromatography Method for the Determination of Ezetimibe in Pharmaceutical Formulations. Anal Sci. 2008;24(4):499–503.
73. Alshehri MM. A validated capillary electrophoresis method for simultaneous determination of ezetimibe and atorvastatin in pharmaceutical formulations. Saudi Pharm J. 2012;20(2):143–148.
74. Yola ML, Ozaltin N. Rev Anal Chem. 2011;30:29–36.
75. Bagary RI, El–Kady EF, Kadry AM. Hinawipublishing corporation. 2012;27:83–92.
76. Gajjar K, Shah VD. J Pharm Biomed Anal. 2011;55:225–229.
77. Santa Z, Koti J, Szoke K, et al. J Pharm Biomed Anal. 2012;58:125–129.
78. Gajjar K, Shah VD. Impurity profiling: a case study of ezetimibe. The Open Conference Proceeding Journal. 2011;2(7):108–112.
79. Darwish HW, Hassan SA, Salem MY, et al. Three different spectrophotometric methods manipulating ratio spectra for determination of binary mixture of Amlodipine and Atorvastatin. Spectrochim Acta A Mol Biomol Spectrosc. 2013;83(1):140–148 .
80. Beebe KR, Pell RJ, Seasholtz MB. Chemometrics: A practical guide, John Wiley& Sons, New York, USA, 1998. 337 p.
81. Zissis KD, Brereton RG, Escott R. Analyst. 1998;123:1165–1173.
82. ICH. Stability Testing Of New Drug Substances and Products. International Conference on Harmonization, Geneva, USA; 1993:1–24.
83. Massart DL, Vandeginste BGM, Deming SN, et al. Chemometrics. 1998. 124 p.
84. Martin, Swarbrick J, Cammarata A. Physical pharmacy. 3rd edn. Lea and Febiger, Philadelphia, USA; 1983:359–360.
85. El–sayed Talanta MA. 2011;83:717–723.
86. Haaland DM, Thomas EV. Anal Chem. 1988;60:1193–1202.
87. Chetan MB, Jane J, Subrahmanyam EVS. Int J Res Pharm Biomed Sci. 2011;2:241–244.