The Method of PID parameters tuning for AMB system at high-frequency

doi:10.15406/iratj.2018.04.00102

eISSN: 2574-8092

International Robotics & Automation Journal

Mini Review Volume 4 Issue 2

The Method of PID parameters tuning for AMB system at high-frequency

Sun Jinji, Zhou Han,

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Ju Ziyan

School of Instrumentation Science & Opto-electronics Engineering, Science and Technology on Inertial Laboratory, Beihang University, China

Correspondence: Zhou Han, School of Instrumentation Science & Opto-electronics Engineering, Science and Technology on Inertial Laboratory, Beihang University, China, Tel 8.61082E+11

Received: January 30, 2018 | Published: March 22, 2018

Citation: Jinji Sun, Han Z, Ziyan J. The Method of PID parameters tuning for AMB system at high-frequency. Int Rob Auto J. 2018;4(2):107-108. DOI: 10.15406/iratj.2018.04.00102

Download PDF

Abstract

With the development of industrial technology, magnetic bearing rotor’s speed is getting higher and higher. When the rotor rotates at a high speed, the current stiffness and displacement stiffness of the magnetic bearing will decrease due to the eddy current effect for any kind of structure. In this paper, the analytical model of dynamic stiffness is deduced considering the influence of eddy current. According to characteristic equation and Routh-Hurwitz criterion, the relationship between the stable ranges of PID parameters and rotor frequency is set up based on dynamic stiffness model. Simulation experiments in Matlab/Simulink are made to verify the correctness of theoretical analysis.

Keywords: active magnetic bearing, dynamic stiffness, PID control

Introduction

Active magnetic bearings (AMBs) are widely applied because of its advantages, the bearing forces are actively controlled by means of electromagnets, a feedback control loop, sensors and power amplifiers.^1–3 In recent research, PID as a mature and effective algorithm is commonly used in magnetic bearing system, and the bearing stiffness is assumed as a constant, which is not affected by rotor frequency for PID controller design.^4,5 Nevertheless, the impact of considerable decrease of AMB stiffness caused by eddy current on system cannot be ignored. Le Yun⁶ studied the influence of eddy current on the dynamic stiffness of the radial differential magnetic bearing with laminated structure, and optimized the structural parameters. Whereas the dynamic stiffness is not considered into control system. For controller design, PID parameters tuning method is significant and the on-line tuning strategy is usually used in industrial debugging. It is obviously that on-line tuning method is hard to take under the high-frequency situation. Therefore, establishing a theoretical standard for PID parameters tuning based on AMB dynamic stiffness is necessary.

Method and analysis

The typical structure of AMB is shown in the Figure 1. By analyzing the dynamic equivalent magnetic circuit mode, the analytical model of dynamic stiffness is established and is presented as (1) and (2). The relative permeability (μr) of stator and rotor are deduced respectively.⁷

$k_{i} = \frac{32 N^{2} I}{ρ^{2} μ_{0} l_{a} l_{p}} . \cos ({22.5}^{0}) . {[\frac{2 g}{μ_{0} l_{a} l_{p}} + \frac{π (r_{s o} + r_{e i}) \sqrt{i ω σ μ_{0} μ_{r}} \frac{d}{2}}{8 μ_{0} l_{a} l_{p} (r_{s o} - r_{e i}) \tanh (\sqrt{i ω σ μ_{0} μ_{r}} \frac{d}{2})} + \frac{d π (r_{s o} + r_{e i} - 2 r_{s i}) \sqrt{i ω σ μ_{0} μ_{r}}}{2 μ_{0} l_{a} l_{p} t a n h (\sqrt{i ω σ μ_{0} μ_{r}} \frac{d}{2})} + \frac{π (r_{s o} + r_{e i}) \sqrt{2 i ω σ μ_{0} μ_{r}} \frac{d}{2}}{8 μ_{0} l_{a} l_{p} (r_{s o} - r_{e i}) \tanh (\frac{d}{2} \sqrt{i ω σ μ_{0} μ_{r}})}]}^{- 2}$ (1)

$k_{y} = \frac{64 N^{2} I^{2} \cos^{2} ({22.5}^{0})}{ρ^{2} μ_{0}^{2} l_{a}^{2} l_{p}^{2}} . {[\frac{π (r_{s o} - r_{e i})}{8 μ_{0} μ_{r} l_{a} (r_{s o} - r_{e i})} + \frac{r_{s o} + r_{e i} - 2 r_{s i}}{μ_{0} μ_{r} l_{a} l_{p}} + \frac{π d (r_{r o} + r_{r i}) \sqrt{i ω σ μ_{0} μ_{r}}}{8 μ_{0} μ_{r} l_{a} (r_{s o} + r_{r i}) \tanh (d \sqrt{i ω σ μ_{0} μ_{r}})} + \frac{2 g}{μ_{0} μ_{r} l_{a}}]}^{- 3}$ (2)
The AMB controlled by digital PID mainly consists of electromagnet, rotor, displacement sensor, PID controller and power amplifier. For Y-direction, the AMB control schematic diagram is shown in Figure 2.

Figure 1 Structure of the AMB.

Figure 2 AMB Control Principle for Y-direction.

Considering the impact of high-frequency noises, the PID controller usually use incomplete differential replace the typical differential. The transfer function of rotor is shown as (3), where

| k_{y} (ω) |

and

| k_{i} (ω) |

are respectively the amplitude of displacement stiffness and current stiffness.

T_{y} (ω)

and

T_{i} (ω)

could be expressed as

T_{y} (ω) = - \tan (ϕ_{k i}) / ω

and

T_{i} (ω) = - \tan (ϕ_{k y}) / ω

, where

ϕ_{k y}

and

ϕ_{k i}

are the changes of

k_{y}

and

k_{i}

phrase compared to static stiffness.

G_{z} (w) = \frac{| k_{i} (ω) |}{m T_{y} (ω) s^{3} + m s^{2} + | k_{y} (ω) |} . \frac{1 + T_{y} (ω) s}{1 + T_{i} (ω) s}

(3)

Displacement sensor and power amplifier adopted the typical model.⁸ Let the integral part coefficient $(K_{i})$ of PID controller equals to 0 and the closed-loop transfer function of AMB system is shown as (4). Where $k_{a}$ , $k_{m}$ and $k_{c}$ are the amplification factor of AD, power amplifier and sensor respectively. R is the resistance of coil, L is the inductance of coil and m is the mass of rotor. $K_{p}$ is the proportional coefficient, $K_{d}$ is the differential coefficient and $T_{d}$ is the differential time constant. The steady state error of the system depends on the parameter $K_{i}$ .
$G = k_{a} . (K_{p} + \frac{K_{d} s}{1 + T_{d} s}) . \frac{k_{m}}{L s + R + k_{m} k_{a} k_{i c o} k_{c}} . \frac{| k_{i} (ω) |}{m T_{y} (ω) s^{3} + m s^{2} + | k_{y} (ω) |} . \frac{1 + T_{y} (ω) s}{1 + T_{i} (ω) s}$ (4)
The stable ranges of $K_{p}$ , $T_{d}$ and $K_{d}$ could be determined by characteristic equation of system and Routh Criterion. And the ranges are the function of rotation speed ω. For AMB systems under constant rotation frequency, once $T_{d}$ is set to a concrete value, the range of $K_{p}$ could be calculated. Similarly, set $K_{p}$ to a certain value and the stability range of $K_{d}$ can be obtained. Several simulations are taken to verify the correctness of the above method proposed, the results is that AMB system is stable at different frequency when the parameters are selected in corresponding ranges (Figure 3), otherwise the unit step response diverges.

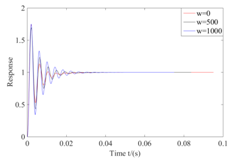
Figure 3 Unit Response of AMB system.

Conclusion

In this paper, the analytical model of dynamic stiffness under the influence of eddy current effect is deduced. The method to accurately determine the stable range of PID parameters at different speeds is proposed. The simulations executed in MATLAB/Simulink and the result can prove the correctness of the PID parameters ranges. In general, it is a great significance to adjust PID parameters at high rotation speed and lay the foundation for the higher speed of magnetic bearings.

Acknowledgements

My research project was partially or fully sponsored by the Excellent Youth Science Foundation of China (Grant No.51722501), by the National Natural Science Foundation of China (Grant No.51575025), and by the Preliminary Exploration of Project (Grant No.7131474). In case of no financial assistance for the research work, provide the information regarding the sponsor.