Study on the model of quantification of syndromes and identification of syndrome types classification of hypertension based on facial color spectral decomposition technology

doi:10.15406/iratj.2020.06.00203

eISSN: 2574-8092

International Robotics & Automation Journal

Research Article Volume 6 Issue 2

Study on the model of quantification of syndromes and identification of syndrome types classification of hypertension based on facial color spectral decomposition technology

Kai Li,¹

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Xiaoyu Ma,² Rong Ni,³ Jiali Liu,¹ Bin Wu⁴

¹Center for Chinese Medicine Big Data and Smart Health Research, Zhejiang Chinese Medical University, China
²Institute of Intelligent Media Technology, Communication University of Zhejiang, China
³Micro Medical Group (Zhejiang) Co., Ltd, China
⁴The Third Affiliated Hospital of Zhejiang Chinese Medical University, China

Correspondence: Kai Li, Center for Chinese Medicine Big Data and Smart Health Research, Zhejiang Chinese Medical University, China, Tel +86-15268500555, Fax 0086-571-86610109

Received: March 29, 2020 | Published: May 15, 2020

Citation: Li K, Ma X, Ni R, et al. Study on the model of quantification of syndromes and identification of syndrome types classification of hypertension based on facial color spectral decomposition technology. Int Rob Auto J . 2020;6(2):68?78. DOI: 10.15406/iratj.2020.06.00203

Download PDF

Abstract

Objective: In this paper, the classification quantification and intelligent identification of traditional Chinese medicine (TCM) syndromes of hypertension based on facial image information are studied by the method of combination of medicine and engineering.

Methods: Firstly, the research on the combination of TCM syndrome quantification and hypertension blood pressure levels and the application of chromatographic decomposition technology to the extraction of TCM facial features are innovatively explored. Secondly, on the basis of the above research and combining with the machine learning algorithm, the hierarchic and quantitative intelligent diagnosis model of TCM syndromes of hypertension is constructed, which realizes the intelligent classification and quantification of TCM syndrome types of hypertension, based on the accurate analysis of the subtle differences in the color features of each facial region of different TCM syndrome types of hypertension.

Results：Syndrome identification accuracy and classification accuracy of overabundant liver-fire syndrome, Yin deficiency with Yang hyperactivity, Yin and Yang deficiency syndrome, and healthy persons in the test respectively reach 68%/74%, 75%/72%, 70.8%/72%, 80%/-, with a good identification effect, but that of excessive accumulation of phlegm-dampness only reach 58.3%/66%, whose model identification effect is not obvious.

Conclusions：For the study of small sample size in the field of intelligent diagnosis of hypertension with TCM syndromes, the diagnosis model based on color spectral decomposition (CSD) and random forest (RF) is more effective than the diagnosis model based on DNN. The CSD algorithm for syndrome color extraction and analysis proposes a new model of intelligent diagnosis of the classification and quantification of TCM syndromes in hypertension. This paper uses indirect methods to measure the syndromes and the evolution of syndromes in a non-wound manner. Judging the degree of target organ damage and home rehabilitation for the patients with hypertension makes this study of great research significance and application prospects.

Key words: Classification and quantification of traditional Chinese medicine syndromes of hypertension, color spectral decomposition technology, quantification of facial image syndromes

Introduction

The intelligent diagnosis of the traditional Chinese medicine (TCM) syndromes of hypertension belongs to the medical intelligence research field which is the intersection between traditional Chinese medicine diagnosis and information science. TCM syndromes is a significant factor affecting people to suffer from hypertension.^1,2 The research method of combination of diseases and syndromes based on syndrome differentiation and dialectical treatment is an inherent and unique content of TCM,³ which has a significant effect in the clinical treatment and prevention of hypertension,^4–6 Intelligent diagnosis of TCM syndromes of hypertension can indirectly judge the degree of target organ damage and be used for home rehabilitation to the patients with hypertension by measuring the syndromes and the degree of syndrome evolution in a non-wound manner at home without biochemical examination in hospital, which makes this research very significant and promising. However, at present, the diagnosis of hypertension in traditional Chinese medicine is based on the symptoms (the objective characteristics of various parts of the human body in the disease state). Hypertension is diagnosed into four syndromes (Overabundant Liver-Fire Syndrome；Yin Deficiency with Yang Hyperactivity；excessive accumulation of phlegm-dampness；Yin and Yang deficiency syndrome).⁷ The biggest drawback is that each syndrome has only a name and no severity level, so it is impossible to quantify the morbidity like blood pressure value diagnosis of western medicine and then give a timely warning when the blood pressure is higher.^8–13

In recent years, the intelligent machine learning image processing algorithm has been widely applied in the field of modern medical image recognition.^14,15 It is still in its infancy in the digital image recognition of face image, tongue image and pulse in traditional Chinese medicine,¹⁶ which are always used for constitution identification.¹⁷ Besides, the sign image detection algorithm for single diseases is now still vacant^18,19 and the intelligent detection standards need to be improved. At present, the main method for facial chroma characterization is three-dimensional index in a specific color space, including RGB HSV²⁰CIE²¹ and so on. In many image processing tasks, that redundant and sparse representation often yield better results compared to compact representations. For example, image quality assessment algorithms such as VIF²² MS-SSIM,²³FR-DOG,²⁴ and MAD²⁵ tend to decompose the image into several sub-bands^26,27 in the pre-processing stage. Considering that, a new chroma representation method namely color spectral decomposition is developed to transform the three-dimensional color index into a sparse vector which can benefit the extraction of distinguishing features of facial colors of various TCM syndromes.

This study is to realize the hierarchic and quantitative intelligent diagnosis of the four syndrome types of hypertension in traditional Chinese medicine through the analysis of objective images of syndromes, and achieve the correspondence and mutual interpretation between the severity level of TCM syndromes of hypertension and the blood pressure values of hypertension in western medicine. The innovation of this paper is to explore the hierarchic and quantitative intelligent diagnosis model of TCM syndromes of hypertension through the establishment of a chromatographic analysis algorithm that is more suitable for color extraction and analysis in small sample size syndromes.

Methodology

Based on the previous introduction, this paper proposes the following hypothesis: different facial colors play an important role in the prediction and classification of TCM syndrome types of hypertension.

In order to verify the scientific hypothesis, these works firstly determine several facial regions that are supposed most relevant to TCM syndromes via Analytic Hierarchy Process (AHP) fuzzy comprehensive evaluation method. Then intelligent diagnosis models are designed to extract the distinguishing color features and predict the TCM syndromes given the selected facial regions. Two types of diagnosis model are proposed and the overall pipeline is shown as Figure 1.

Figure 1 Overall pipeline of TCM diagnosis model.

Intuitively, deep learning techniques might be an optimal solution to extract distinguishing color information, considering its powerful potency of abstraction and representation. However, several factors could restrict the performance of the diagnosis model based on DNN:

Color differences of various TCM syndromes are subtle in Red, Green, Blue (GRB) color space. Whether the diagnosis model based on DNN can capture the subtle difference requires further validation.
Due to the difficulty of the facial information collection of the patients with hypertension, the training samples are limited, which will aggravate the difficulty of extracting the subtle difference in RGB color space.

Considering that, explicit hand-craft feature extraction methods might be another feasible way. Specifically, we also developed a color spectral decomposition (CSD) algorithm to capture the subtle distinguishing color features and employ traditional regression tools (e.g., RF) to aggregate the features and predict the TCM syndromes. The detailed description of the AHP evaluation method and the two diagnosis models are depicted as follow:

Fuzzy evaluation of TCM diagnostic knowledge based on AHP algorithm

Traditional Chinese medicine believes that color changes in different parts of the human body indicate different diseases, and the face, nose, cheeks, lips, and eyes are divided into different organs to diagnose and predict diseases.²⁸ Lingshu Five colors points out that the pathological position, severity level of the disease can be judged by observing the depth of complexion. You can understand the position of viscera limb segment and other lesions by observing the position of the sickly complexion. That is, if the sickly complexion is undertint, the disease is light, while, if it is dark, the disease is serious. Hypertension is characterized in different parts. Jing Sun et al., (2014)²⁹ proposed that patients with hypertension could be treated according to the characteristics of the forehead, nose, ear, cheek, tongue, eye and hand. Different syndromes of hypertension show different color features in facial regions.³⁰ The identification of TCM syndrome types of hypertension mainly depends on the experience of clinical experts in diagnosis. Due to lacking for the normative quantitative objectification criteria, it’s difficult to achieve the intelligent detection and monitoring of the evolution degree of hypertension based on combination of diseases and syndromes. Based on previous studies, this paper uses the AHP fuzzy comprehensive evaluation method to determine the regions with significant facial color features of hypertension. The algorithm adopted in this paper is as follows:

The evaluation index system of the facial partition of the patients with hypertension is composed of the first and second index layers, and the first index set is $U = {U_{1,} U_{2,} U_{3}}$ $U = {U_{1,} U_{2,} U_{3}}$ .

Let the first-level index $U_{i} (i = 1, 2, 3)$ $U_{i} (i = 1, 2, 3)$ have $M_{i}$ $M_{i}$ second-level indexes, denoting as $U_{i} = {U_{i 1}, U_{i 2}, \dots, U_{i j}} (i = 1, 2, 3; j = 1, 2, \dots, m)$ $U_{i} = {U_{i 1}, U_{i 2}, \dots, U_{i j}} (i = 1, 2, 3; j = 1, 2, \dots, m)$ , and $U_{i j}$ $U_{i j}$ as the $j$ $j$ ^th second-level index of $U_{i}$ $U_{i}$ .

This paper adopts AHP method, and sets the weight of $U_{i}$ $U_{i}$ as $a_{i} (i = 1, 2, 3)$ $a_{i} (i = 1, 2, 3)$ , then the first-level weight set is: $A = {a_{1,} a_{2,} a_{3}}, 0 a_{i} 1, \sum_{i = 1}^{3} a_{i} = 1$ $A = {a_{1,} a_{2,} a_{3}}, 0 a_{i} 1, \sum_{i = 1}^{3} a_{i} = 1$ .

Let the weight of the second-level index $U_{i j}$ $U_{i j}$ be $a_{i j} (i = 1, 2, 3; j = 1, 2, \dots, m)$ $a_{i j} (i = 1, 2, 3; j = 1, 2, \dots, m)$ , then the second-level weight set is $A_{i} = {a_{i 1}, a_{i 2}, \dots, a_{i m_{i}}}, 0 a_{i j} 1, \sum_{j = 1}^{m_{i}} a_{i j} = 1, i = 1, 2, 3; j = 1, 2, \dots, m_{i}$ $A_{i} = {a_{i 1}, a_{i 2}, \dots, a_{i m_{i}}}, 0 a_{i j} 1, \sum_{j = 1}^{m_{i}} a_{i j} = 1, i = 1, 2, 3; j = 1, 2, \dots, m_{i}$ .

Evaluation grade is the basis for evaluation and measurement of facial partition. The evaluation set is divided into 5 grades, which are expressed as $V = {very fit, relatively fit, fit, barely fit, not fit}$ $V = {very fit, relatively fit, fit, barely fit, not fit}$ in the indicator system. That is, the weight ratio of the secondary indicators will be calculated according to the selection of the team of clinical experts on hypertension.

According to the judgment of experts, each factor $U_{i j}$ $U_{i j}$ of $U_{i}$ $U_{i}$ has a degree of membership to the five review levels $(r_{i j 1}, r_{i j 2}, \dots, r_{i j 5})$ $(r_{i j 1}, r_{i j 2}, \dots, r_{i j 5})$ , and the evaluation results of $M_{i}$ $M_{i}$ factors can be expressed as a fuzzy matrix $R_{i}$ $R_{i}$ of order $M_{i} \times 5 ：$ $M_{i} \times 5 ：$

$R_{i} = ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ \begin{matrix} \begin{matrix} \begin{matrix} r_{i 11} r_{i 21} \end{matrix} & \begin{matrix} r_{i 12} r_{i 22} \end{matrix} \end{matrix} & \begin{matrix} \dots \dots \end{matrix} & \begin{matrix} r_{i 11} r_{i 25} \end{matrix} \begin{matrix} ⋮ & ⋮ \end{matrix} & ⋱ & ⋮ \begin{matrix} r_{i m_{i} 1} & r_{i m_{i} 2} \end{matrix} & \dots & r_{i m_{i} 5} \end{matrix} ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ (i = 1, 2, 3)$ $R_{i} = [\begin{matrix} \begin{matrix} \begin{matrix} r_{i 11} \\ r_{i 21} \end{matrix} & \begin{matrix} r_{i 12} \\ r_{i 22} \end{matrix} \end{matrix} & \begin{matrix} \dots \\ \dots \end{matrix} & \begin{matrix} r_{i 11} \\ r_{i 25} \end{matrix} \\ \begin{matrix} ⋮ & ⋮ \end{matrix} & ⋱ & ⋮ \\ \begin{matrix} r_{i m_{i} 1} & r_{i m_{i} 2} \end{matrix} & \dots & r_{i m_{i} 5} \end{matrix}] (i = 1, 2, 3)$

$R_{i}$ $R_{i}$ is the single-factor evaluation matrix of the first-level index fuzzy comprehensive evaluation of $U_{i}$ $U_{i}$ , where $r_{i j n}$ $r_{i j n}$ is the degree of membership of $U_{i j}$ $U_{i j}$ which is rated as grade $n (n = 1, 2, \dots, 5)$ $n (n = 1, 2, \dots, 5)$ . According to the determined weight set $A_{i}$ $A_{i}$ , the first-level index fuzzy comprehensive evaluation matrix of y is:

$C_{i} = A_{i} R_{i} = (a_{i 1}, a_{i 2}, \dots, a_{i m_{i}}) ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ \begin{matrix} \begin{matrix} \begin{matrix} r_{i 11} r_{i 21} \end{matrix} & \begin{matrix} r_{i 12} r_{i 22} \end{matrix} \end{matrix} & \begin{matrix} \dots \dots \end{matrix} & \begin{matrix} r_{i 11} r_{i 25} \end{matrix} \begin{matrix} ⋮ & ⋮ \end{matrix} & ⋱ & ⋮ \begin{matrix} r_{i m_{i} 1} & r_{i m_{i} 2} \end{matrix} & \dots & r_{i m_{i} 5} \end{matrix} ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ = (c_{i 1}, c_{i 2}, \dots, c_{i m_{i}})$ $C_{i} = A_{i} R_{i} = (a_{i 1}, a_{i 2}, \dots, a_{i m_{i}}) [\begin{matrix} \begin{matrix} \begin{matrix} r_{i 11} \\ r_{i 21} \end{matrix} & \begin{matrix} r_{i 12} \\ r_{i 22} \end{matrix} \end{matrix} & \begin{matrix} \dots \\ \dots \end{matrix} & \begin{matrix} r_{i 11} \\ r_{i 25} \end{matrix} \\ \begin{matrix} ⋮ & ⋮ \end{matrix} & ⋱ & ⋮ \\ \begin{matrix} r_{i m_{i} 1} & r_{i m_{i} 2} \end{matrix} & \dots & r_{i m_{i} 5} \end{matrix}] = (c_{i 1}, c_{i 2}, \dots, c_{i m_{i}})$

Among them, ° is a composition operator.

The single factor evaluation matrix R of comprehensive fuzzy evaluation is composed of the fuzzy judgment matrix $C_{i} (i = 1, 2, 3)$ $C_{i} (i = 1, 2, 3)$ of the first-level index. The comprehensive evaluation model is:

$R = ⎡ ⎢ ⎣ \begin{matrix} C_{1} \begin{matrix} C_{2} C_{3} \end{matrix} \end{matrix} ⎤ ⎥ ⎦ = ⎡ ⎢ ⎣ \begin{matrix} A_{1} R_{1} A_{2} R_{2} A_{3} R_{3} \end{matrix} ⎤ ⎥ ⎦ = {(c_{i m})}_{3 \times 5}$ $R = [\begin{matrix} C_{1} \\ \begin{matrix} C_{2} \\ C_{3} \end{matrix} \end{matrix}] = [\begin{matrix} A_{1} R_{1} \\ A_{2} R_{2} \\ A_{3} R_{3} \end{matrix}] = {(c_{i m})}_{3 \times 5}$

Therefore, the second-level fuzzy comprehensive evaluation set is:

$C = A R = (a_{1,} a_{2,} a_{3}) ⎡ ⎢ ⎣ \begin{matrix} A_{1} R_{1} A_{2} R_{2} A_{3} R_{3} \end{matrix} ⎤ ⎥ ⎦ = (c_{1}, c_{2}, \dots, a_{5})$ $C = A R = (a_{1,} a_{2,} a_{3}) [\begin{matrix} A_{1} R_{1} \\ A_{2} R_{2} \\ A_{3} R_{3} \end{matrix}] = (c_{1}, c_{2}, \dots, a_{5})$

Finally, according to the index with the largest corresponding weight in the evaluation results, the most suitable facial feature extraction regions to be screened were determined, namely, the cheeks, forehead and nose.

TCM diagnosis model based on CSD+FR

The feature extraction methods elaborately designed, namely color spectral decomposition (CSD), and are proposed to explicitly capture the subtle difference of color information between various types of TCM syndromes. The overall procedure is described as the upper part of Figure 1, and the details are illustrated as follow.³¹

Facial region extraction: According to the AHP results in Section II, the color information in cheeks, forehead and nose of the face is more relevant to the TCM syndromes. Ensemble of Regression Trees³² (implemented by Dlib³³) is employed to automatically localize and extract the 4 facial regions namely A, B, C, and D (representing cheeks, forehead and nose of the face). Considering the tested facial images are captured by standardized equipment and need no calibration, the Ensemble of Regression Tress is preferable due to its light-weight and robustness.

Specifically, the 68 landmarks are localized by Dlib³³ (shown as Figure 2a) and based on several (the 1^st, 3^th , 13^th, 15^th, 21^th, 22^th, 27^th, 28^th, 29^th) of the 68 landmark points we can extract color information from the four specific facial regions, as illustrated in Figure 2b.

Figure 2 Face detection and specific facial region extraction.

Color spectral decomposition: After extraction of facial regions, the proposed color spectral decomposition (CSD) is involved to extract the subtle distinguishing color features in the 4 facial regions. Giving a pixel with color index $[r, g, b]$ $[r, g, b]$ in RGB color space, the color spectral decomposition (CSD) method this paper proposes aims to construct a sparse representation of $[r, g, b]$ $[r, g, b]$ that can transform the three-dimensional color index into a spectral vector with N dimension where N>>2, i.e., $s = T_{C S D} ([r, g, b])$ .

The color index $[r, g, b]$ is firstly converted into HSV color space as $[h, s, v]$ ( $h, s, v$ denote the hue, saturation, and luminance respectively;¹⁹ the values of s,v are in the range of [0,1] and the value of h is in the range of [ $0, 2 π$ ], which are demonstrated as Figure 3.

Figure 3 An illustration of HSV color space.

N solid colors with uniformly-spaced hue difference are selected as anchor points, which are denoted as $(p^{0}, p^{�}, p^{2 �}, \dots, p^{2 π - �})$ , where $Δ = \frac{2 π}{N}$ . The intensity of p that is projected to $(p^{0}, p^{�}, p^{2 �}, \dots, p^{2 π - �})$ is calculated respectively as described in Figure 4.

Figure 4 An illustration of intensity calculation.

As shown in Figure 4, the red circle denotes all the solid colors in HSV color space, i.e., $h \in [0, 2 π], s = 1, v = 1$ . N solid colors $(p^{0}, p^{�}, p^{2 �}, \dots, p^{2 π - �})$ are represented by blue circles. The intensity of p which is projected to a solid color $p^{k Δ}$ is defined as the function of the distance between p and $p^{k Δ}$ . Supposing the color index of p is $[h_{p}, s_{p}, 1]$ and $p^{k Δ}$ is $[h_{i}, 1, 1]$ , their distance then can be derived as $d_{p}^{k} = \sqrt{1 - 2 s_{p} c o s θ + s_{p}^{2}}$ . The analysis above is focused on colors with full luminance, i.e., $v_{p} = 1$ . For an arbitrary p with color index $[h_{p}, s_{p}, v_{p}]$ , its distance can be derived as $d_{p}^{k} = \sqrt{1 - 2 s_{p} c o s θ + s_{p}^{2} + {(1 - v_{p})}^{2}}$ .

A function $f (x) = e^{- \frac{x^{2}}{λ}}$ is employed to map the distance between p and $p^{k Δ}$ to the intensity of p which is observed on $p^{k Δ}$ . Therefore, the intensity of p projected to $p^{k Δ}$ , denoted as $s_{k}$ , can be derived as

$s_{k} = exp (- \frac{1 - 2 s_{p} c o s θ + s_{p}^{2} + {(1 - v_{p})}^{2}}{λ})$ (1)

λ is employed to control the attenuation of intensity. For instance, if the saturation and luminance of p is near to 1, then its intensity should concentrate in its nearest solid colors. On the contrary, if its saturation and luminance is significantly smaller than 1, its intensity should also spread a larger range of solid colors. In view of that, we set $λ = λ_{0} + \frac{{(1 - s_{p})}^{2} + {(1 - v_{p})}^{2}}{5}$ where $λ_{0}$ is set to 0.1. A N-dimensional spectral vector $s = [s_{1}, \dots, s_{N}]$ can be got by iterating all anchor points.

Supposing that four image patches $x_{A}, x_{B}, x_{c}, x_{D}$ represent 4 different facial regions of a facial image respectively, each region is transformed via color spectral decomposition pixel-wise. For instance, all pixels $p_{i}^{j} \in x_{i}$ ( $i \in {A, B, C, D},$ and denotes the special index) with color index [ $r_{i}^{j}, g_{i}^{j}, b_{i}^{j}$ ] are converted into HSV color space, whose corresponding spectral vector $s_{i}^{j}$ is calculated according to Eq.(1). It should be noticed that the hue of facial regions always concentrates in a limited range, which is about from 0.03 $π$ to 0.1 $π$ based on the observation of approximate 250 subjects. Therefore, the hue of each pixel p, denoted as h_p, is mapped to range [0,1] by $m a p (h_{p}) = \frac{h_{p} - 0.03 π}{0.07 π}$ . A demonstration of spectral vectors extracted from the four facial regions is shown as Figure 5, in which the horizontal axis denotes the hue of solid colors that is used as anchor and the vertical axis denotes the Intensity. N is set to 100 to show the detailed features of spectral vectors, which can also be set to other values. The spectral vectors in the same region are plotted in one single sub-figure.

Figure 5 An illustration of spectral vectors in different regions.

The central spectral vectors of region i, denoted as $c s^{i}, i \in {A, B, C, D}$ , can be calculated by simply averaging all spectral vectors in the given region after outlier exclusion, which is illustrated as Eq.(2)

$c s^{i} = \frac{\sum_{j \in i'} s_{i}^{j}}{# {i'}}$ (2)

i denotes the region after outlier exclusion and $# {i'}$ denotes the number of pixels in region i. The outlier exclusion procedure is employed to eliminate singular spectral vectors that are quite different from the mean vector, and 20% pixels (or structural vectors) are excluded. At last, the kurtosis, skewness, average and standard value of $c s^{i}$ are extracted as statistical features.

TCM syndrome classification and quantification based on machine learning: The kurtosis, skewness, average and standard value of four central spectral vectors ( $c s^{A}, c s^{B}, c s^{C}, c s^{D}$ ) derived from the four facial regions, is denoted as $\vec{s f} = [k u r t o s i s (c s^{A}), s k e w n e s s (c s^{A}), m e a n (c s^{A}), s t d (c s^{A}), k u r t o s i s (c s^{B}), \dots]$ . They are served as inputted features and fed into the machine learning tools in order to predict the level of hypertension and the type of syndromes. The overall flowchart is depicted in Figure 6. Random forest algorithm [1] is served as the machine learning tools.

Figure 6 The overall flowchart of the model of quantification of syndromes of hypertension.

The prediction is comprised of two stages. For instance, supposing the 16-D as inputted features $\vec{s f}$ in the first stage, random forest algorithm A can classify the given facial images into one of the four types of TCM syndromes or healthy people. In the second stage, the centroid is obtained by averaging all the inputted eigenvectors of the same syndrome type and the same level in the training set. The Euclidean Distance between the inputted characteristics of the patients to be predicted and the corresponding centroid of the three levels of each corresponding syndrome type is calculated respectively, and the closest level is taken as the level of the patients to be predicted. It should be noted that if the prediction results in the first stage are healthy, the prediction in the second stage will be terminated in advance.

TCM diagnosis model based on deep neural networks (DNN)

As shown in the lower part of Figure 1, a TCM diagnosis model based on Deep Neural Networks (DNN) is designed as comparison. Considering the limited training samples, the DNN framework is trained in a two-stage manner. Firstly, the Hour-Glass convolutional neural network (CNN) is trained in a self-supervised way to learn a low-dimensional representation in feature domain. Secondly, the CNN-extracted feature is employed to classify the TCM syndrome types via two fully connected layers. The detailed pipeline of the diagnosis model based on DNN is shown as Figure 7.

Figure 7 The flowchart of TCM diagnosis model based on DNN.

The input of the DNN is the channel-wise concatenation of Region A, B, C, D. Each region is resized into 128x128x3 with RGB format. The input size is therefore 128x128x12. In training stage I, the input X is fed into self-supervised CNN that contains an encoder $P (\cdot)$ and a decoder $Q (\cdot)$ , which is similar as Ronneberger O, et al.³² The encoder is comprised of 4 down-blocks, each of which contains two convolutional layers with kernel size 3x3 and activated by Leaky Re Lu.³⁴ A batch normalization layer and a max-pooling layer with size 2x2 is also included in down-blocks. After the 4th down-blocks, the feature map goes through an inception layer whose convolutional kernel size is 1x1. The decoder $Q (\cdot)$ is the inversion of encoder, which is comprised of 4 up-blocks. The structure of up-blocks is similar with that of down-blocks; the difference is the 1st layer in up-blocks is an up-sampling layer acting as the inversion of max-pooling.

As for the training stage II, the pre-trained encoder is fine-tuned by the labels indicating the syndrome types. The feature maps after inception layer is max-pooling and min-pooling channel-wise to obtain a feature vector with size 512x1, and such feature vector is then fed into $g (\cdot)$ to predict the TCM syndromes. The training of the second stage is end-to-end, which means that the parameters in encoder is also trainable in training stage II. Since the training samples are limited, data augmentation is involved by rotating the facial regions 90, 180, 270 degrees respectively.

Experimental results

Training protocol

In this paper, a total of 250 samples of 50 patients with overabundant liver-fire syndrome (OLF), 50 patients with Yin deficiency with Yang hyperactivity (YDYH), 50 patients with excessive accumulation of phlegm-dampness (EAPD), 50 patients with Yin and Yang deficiency syndrome (YYD), and 50 healthy patients are tested. TCM syndromes and level distribution of patients are shown in Table 1.

TCM syndrome types	Number of samples	Number of samples of blood pressure at all levels
TCM syndrome types	Number of samples	I degree	II degree	III degree
Over abundant liver-fire syndrome	50	24	18	8
Yin deficiency with Yang hyperactivity,	50	21	16	13
Excessive accumulation of phlegm-dampness	50	17	19	14
Yin and Yang deficiency syndrome	50	12	21	17
Healthy persons (no syndrome)	50	-	-	-

Table 1 Distribution of TCM Syndromes and Blood Pressure Levels

As for both the training of diagnosis model based on CSD+RF and DNN, about 50% of each type and level are randomly selected as the training set and the remaining data as the test set. When the number of data is an odd number, round up to an integer. Thus, the number of training samples in the five labels of OLF, YDYH, EAPD, YYD and healthy persons is 25,26,26,26,25 respectively. In total, 128 samples are used as the training set and 122 samples as the test set.

Experimental results of diagnosis model based on CSD+RF

The overall flowchart of the proposed diagnosis model based on CSD+RF is shown as Figure 6, and the detailed predicting performance in the testing set is shown in the following confusion matrix (Figure 8), in which the vertical axis represents the ground-truth label, and the horizontal axis represents the prediction. OLF, YDYH, EAPD and YYD represent overabundant liver-fire syndrome, Yin deficiency with Yang hyperactively, excessive accumulation of phlegm-dampness and Yin and Yang deficiency syndrome respectively.

Figure 8 Confusion matrix of stage I prediction.

As can be seen from the above confusion matrix, in general, the overall accuracy of the classifier in the stage I of the test set is 70.5%. The prediction accuracy of OFL, YDYH, EAPD, YYD and healthy persons is respectively 68.0%75.0%, 58.3%, 70.8% and 80%. The prediction accuracy of healthy persons is higher, and that of excessive accumulation of phlegm-dampness is the lowest.

The diagnosis model based on CSD+RF will continue to predict the level of syndrome types in the second stage after the TCM syndrome types of patients are classified. In the second stage, it is assumed that the prediction results of the first stage are accurate enough, that is, the types of inputted syndromes are all true values. At this time, according to the inputted characteristics of patients to be predicted and the distance between the centroid of each level and the corresponding syndrome type, the prediction results of the level can be obtained. The prediction accuracy of each syndrome type is shown as Figure 9. In this figure, the vertical axis represents ground-truth label and the horizontal axis represents prediction.

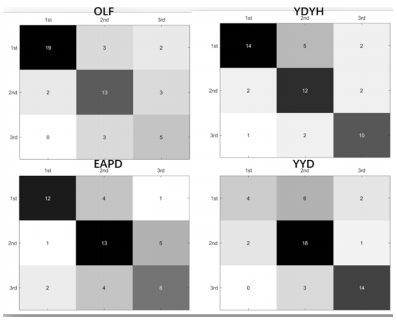
Figure 9 Confusion matrix of stage II prediction.

Experimental results of the diagnosis model based on DNN

As a comparison, the overall flowchart of the diagnosis model based on DNN is shown as Figure 7. The training/testing set division protocol is the same as the framework based on CSD+RF. Considering data augmentation, there are totally 512 training samples for training stage II. In training stage I and II, the minibatch size is 8, and the optimization strategy is Adam, et al.³⁵ with learning rate 0.0005. After the training stage, the training loss of first stage is shown as Figure 10 and the experimental results in testing set is shown as Figure 11.

Figure 10 Training loss of the diagnosis model based on DNN in stage I.

Figure 11 Confusion matrix of the diagnosis model based on DNN.

Performance comparison

The performance comparison in terms of predicting accuracy in testing set between the diagnosis model based on CSD+RF and diagnosis model based on DNN are shown as Figure 12. In 4 (OLF, YDYH, YYD, and Healthy) out of the 5 classes, the diagnosis model based on CSD+RF outperforms the diagnosis model based on DNN by an obvious margin.

Figure 12 Performance comparison between the diagnosis model based on CSD+RF and the diagnosis model based on DNN in terms of accuracy.

Figure 12 indicates that the TCM syndrome diagnosis model based on CNN cannot effectively predict the TCM syndromes in the testing set, demonstrating the superiority of the diagnosis model based on CSD+RF.

We think the limitation of the training samples might be the main reason resulting in the unsatisfied accuracy of diagnosis model based on CNN. Although several tricks (e.g., pre-training stage and data augmentation) are involved aiming to relieve the overfitting problem, 128 original training samples are still insufficient to extract representative color features that relevant to TCM syndromes. On the contrary, the diagnosis model elaborately designed based on CSD+RF can capture distinguishing features of different TCM syndromes. Such feature extraction is explicit; therefore, it can achieve better performance than diagnosis model based on DNN when the training samples are limited. The effectiveness of the diagnosis model based on CSD+RF toward limited training samples are further discussed in ablation experiments.

Ablation experiment

In order to further validate the effectiveness of the proposed TCM syndrome & hypertension level prediction model, several ablation experiments are conducted. Firstly, the results of facial region extraction of several samples are listed to demonstrate that Ensemble of Regression Trees implemented by Dlib is acceptable for facial region extraction in this work, which is shown in Figure 13. The sample data information of this part is shown in Table 2.

Figure 13 Several examples of facial specific region extraction.

serial number	gender	age	blood pressure classification		TCM syndrome types
serial number	gender	age	blood pressure value	level	TCM syndrome types
1	male	55	SBP: 148 mmHg DBP: 87 mmHg	I degree of hypertension	Over abundant liver-fire syndrome
2	male	61	SBP: 148 mmHg DBP: 87 mmHg	I degree of Hypertension	Over abundant liver-fire syndrome
3	male	73	SBP: 151 mmHg DBP: 80 mmHg	I degree of Hypertension	Excessive accumulation of phlegm-dampness
4	female	70	SBP: 153 mmHg DBP: 83 mmHg	I degree of Hypertension	Excessive accumulation of phlegm-dampness
5	male	73	SBP: 142 mmHg DBP: 86 mmHg	I degree of Hypertension	Yin deficiency with Yang hyperactivity
6	female	73	SBP: 145 mmHg DBP: 88 mmHg	I degree of Hypertension	Over abundant liver-fire syndrome
7	female	58	SBP: 149 mmHg DBP: 90 mmHg	I degree of Hypertension	Yin and Yang deficiency syndrome
8	female	50	SBP: 144 mmHg DBP: 89 mmHg	I degree of Hypertension	Yin and Yang deficiency syndrome

Table 2 Sample Data Information

Secondly, some comparisons are illustrated in Figure 14 to validate the effectiveness of the proposed CSD method. The facial regions of 50 samples (10 healthy people and 10 patients from each TCM syndromes) are collected. The central structural vector of region D is then extracted, and the kurtosis and skewness of the central structural vectors are calculated in the end (all regions are effective; region D is randomly selected to validate the color spectral decomposition method.). The distribution of the 50 samples is shown as Figure 14. The horizontal and vertical axis of upper sub-figure respectively denote the kurtosis and skewness of central spectral vectors of facial region D in each subjective. The lower sub-figure denotes several central spectral vectors. Figure 6 demonstrates the proposed color spectral decomposition can effectively extract distinguishing facial chroma features of different types of people.

Figure 14 Feature comparison between healthy people and four TCM syndromes.

Lastly, in order to further validate the effectiveness of the color spectral decomposition, this paper stacks all spectral vectors from region C (region C is also randomly selected) and constructs a matrix of size Mx100, where 100 is the dimension of spectral vector and M is the total number of spectral vectors in region C after outlier elimination. The covariance of the matrix for each TCM syndrome is shown in Figure 15, which further validates that the spectral vectors can extract distinguishing features from different TCM syndromes.

Figure 15 Distinguishing covariance matrix between healthy people and yin and yang deficiency syndrome.

Conclusion and future work

Conclusion

This study designs a simple and easy chromatographic analysis algorithm for the feature extraction and analysis in small sample size and accurate syndrome data based on the medical equipment collected by the four clinics of Chinese medicine Diagnosing the model. On this basis, the hierarchic and quantitative intelligent diagnosis model of TCM syndromes of hypertension is constructed and the scientific hypothesis of TCM Diagnosis Model Based on Deep Neural Networks is verified. Moreover, this paper draws the following research conclusions.

Conclusion 1: this paper has realized the medical explanation between the syndromes of hypertension in traditional Chinese medicine and the blood pressure value in western medicine.

Conclusion 2: syndrome identification accuracy and classification accuracy of overabundant liver-fire syndrome, Yin deficiency with Yang hyperactivity, Yin and Yang deficiency syndrome, and healthy persons with a good identification effect, but that of excessive accumulation of phlegm-dampness, whose model identification effect is not obvious.

Further discussion and limitations of this study

In view of the deficiency such as the low classification and quantification accuracy of identification of excessive accumulation of phlegm-dampness in conclusion 2, we will combine more objective syndrome data such as inquiry, tongue inspection and meridian diagnosis of TCM in the next step to make up for the shortcoming, that the evidence and analysis are incomplete of single complexion data. At the same time, we will improve the generalization ability and prediction accuracy of the model and further expand the sample size. On the basis of large samples, we will design plentiful feature extraction methods and optimize the model.

The "CSD + FR" model designed in this paper has a better performance in intelligent diagnosis of hypertension syndrome because the current research is based on the small sample size, which does not mean that the "CSD + FR" model has an edge over the "DNN" model in the large sample size.

Future work

In the future, based on Zhejiang Chinese Medical University TCM Big Data and Smart Health Research Center and Henan University of Chinese Medicine Intelligent Health Equipment Research Center, the multi-center research will be carried out. The results based on the large sample size will be published and compared with the results of this paper. This paper contributes to the advancement of objective quantitative research on TCM diagnosis of major diseases and the internationalization of TCM.